Функція 10 клас академічний рівень Підготувала Кряжева Олена

“Функція” 10 клас (академічний рівень) Підготувала: Кряжева Олена Петрівна вчитель математики Боровиківського НВК Звенигородської районної ради Черкаської області

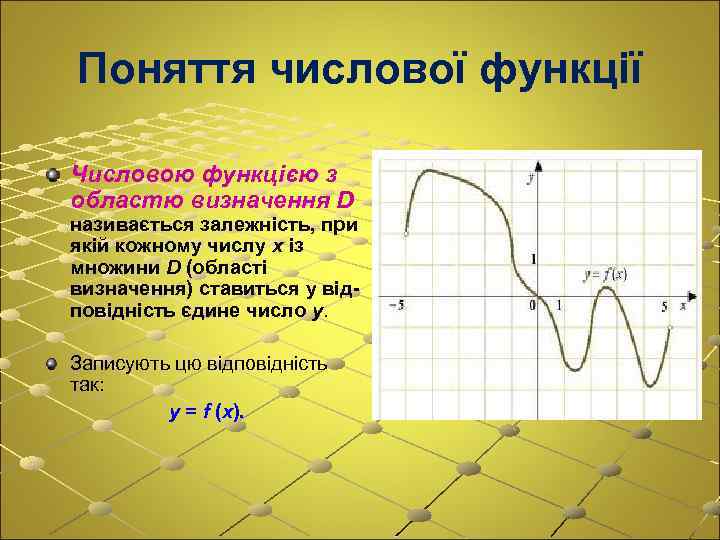Поняття числової функції Числовою функцією з областю визначення D називається залежність, при якій кожному числу x із множини D (області визначення) ставиться у відповідність єдине число y. Записують цю відповідність так: y = f (x).

Позначення і терміни D (f) — область визначення E (f) — область значень x — аргумент (незалежна змінна) y — функція (залежна змінна) f — функція f (x 0) — значення функції f у точці x 0

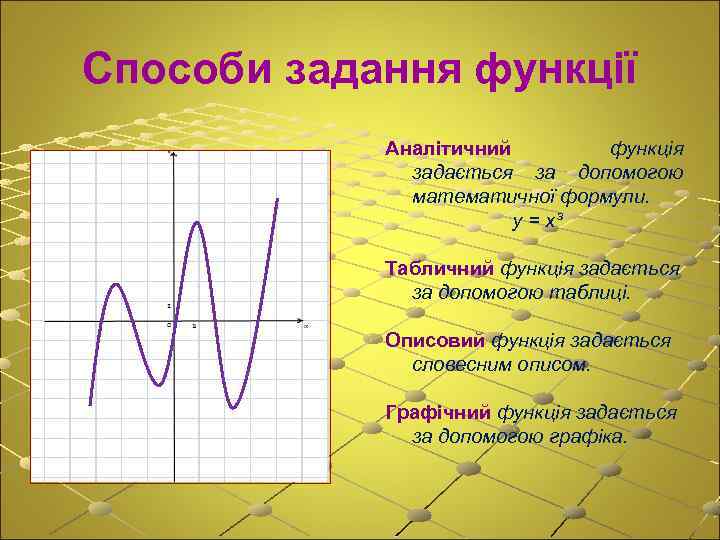Способи задання функції Аналітичний функція задається за допомогою математичної формули. у = х³ Табличний функція задається за допомогою таблиці. Описовий функція задається словесним описом. Графічний функція задається за допомогою графіка.

Приклад 1 Знайдіть область визначення функції: 1) y = x² + x; 2) у = 3) у =

Приклад 2 Знайдіть область значень функції: 1) y = x² – 3. 2) у = – 3 х + 1; 3) у =

Нулі функції Якщо для функції y=f(x) виконується умова f(x 0)=0 (х0 є D(f)), то х0 – нуль функції. х1, х2, х3 – нулі функції (f(x 1)=f(x 2)=f(x 3)=0) проміжки знакосталості функції + -

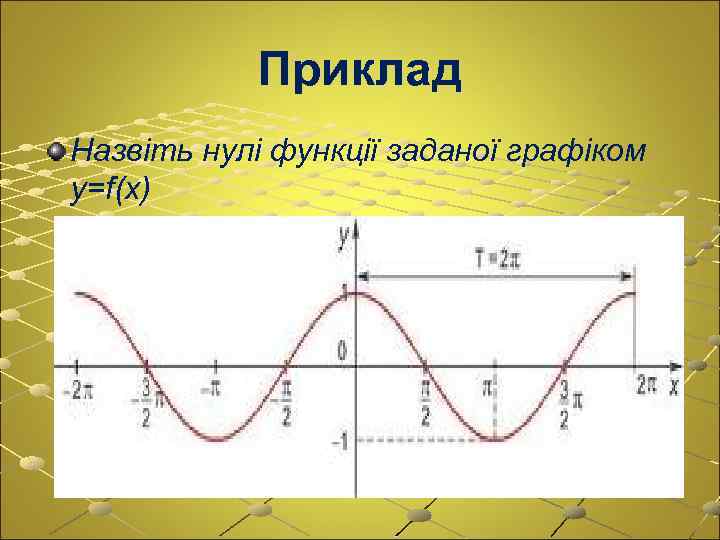Приклад Назвіть нулі функції заданої графіком y=f(x)

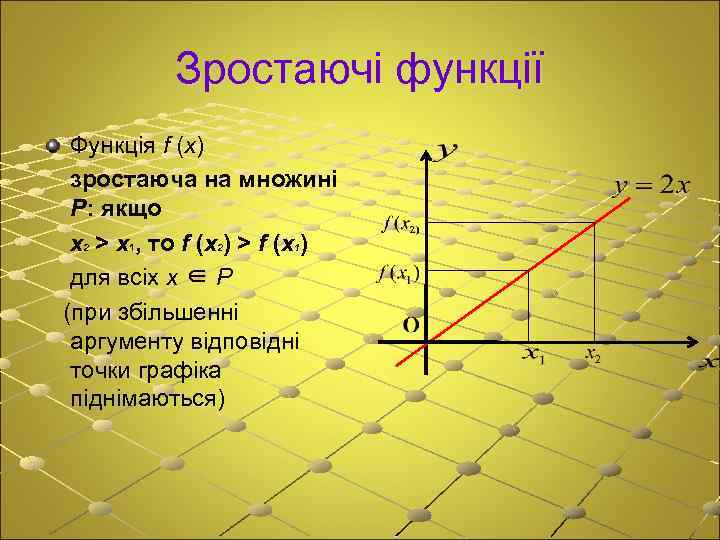Зростаючі функції Функція f (x) зростаюча на множині P: якщо x 2 > x 1, то f (x 2) > f (x 1) для всіх x ∈ P (при збільшенні аргументу відповідні точки графіка піднімаються)

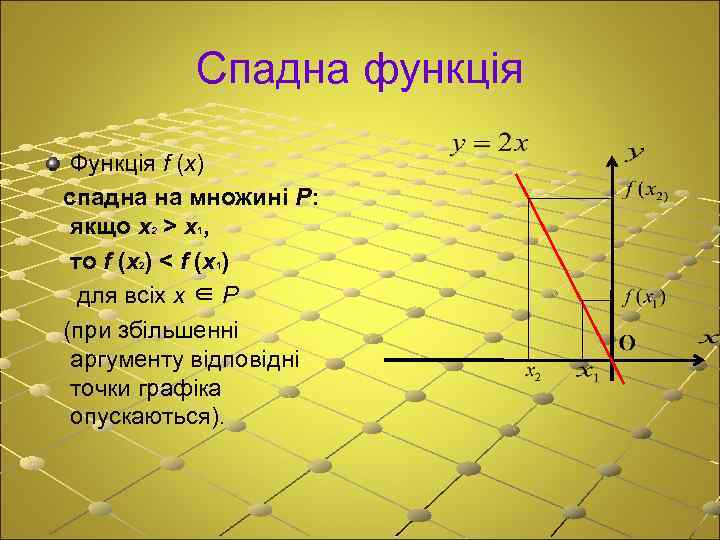Спадна функція Функція f (x) спадна на множині P: якщо x 2 > x 1, то f (x 2) < f (x 1) для всіх x ∈ P (при збільшенні аргументу відповідні точки графіка опускаються).

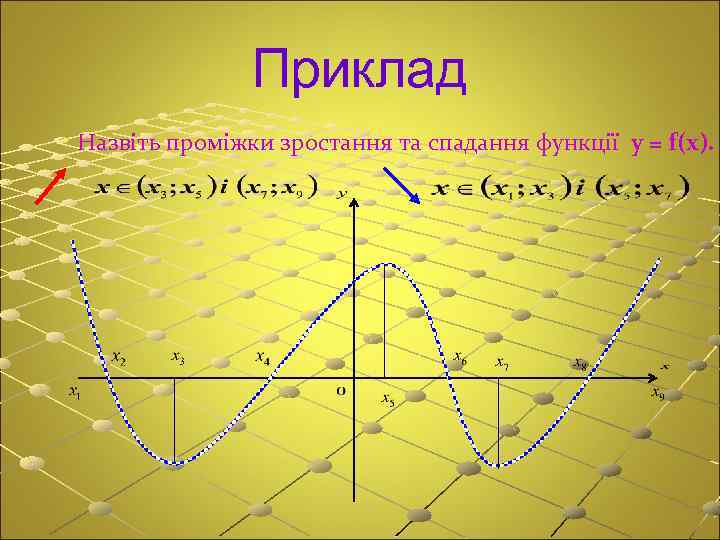Приклад Назвіть проміжки зростання та спадання функції y = f(x).

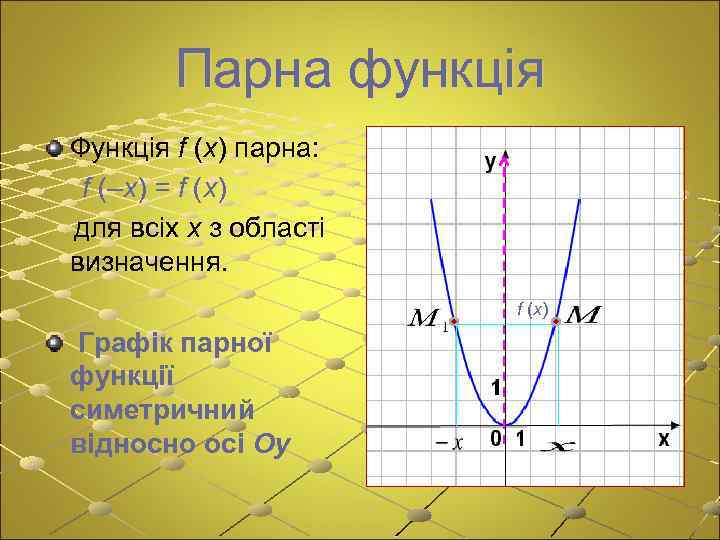Парна функція Функція f (x) парна: f (–x) = f (x) для всіх x з області визначення. f (x) Графік парної функції симетричний відносно осі Oy

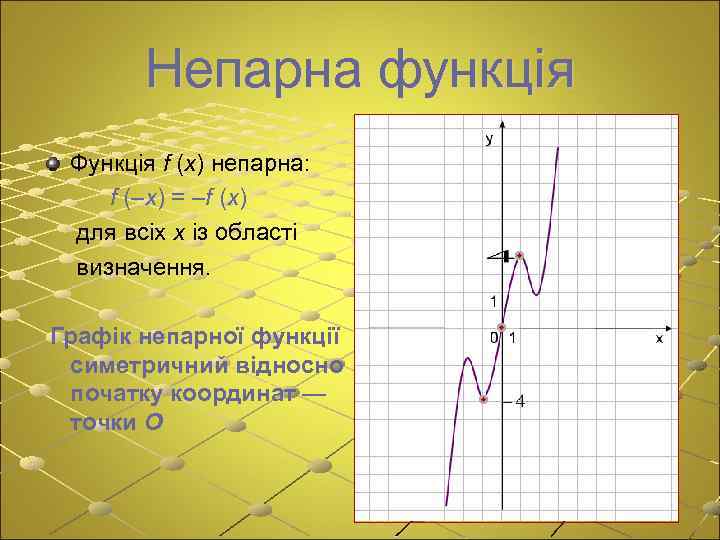Непарна функція Функція f (x) непарна: f (–x) = –f (x) для всіх x із області визначення. Графік непарної функції симетричний відносно початку координат — точки О

Приклад Доведіть, що при k ≠ 0 областю значень лінійної функції y = kx + b є множина всіх дійсних чисел. РОЗВ’ЯЗАННЯ: КОМЕНТАР Якщо kx + b = a (де k ≠ 0), то розв’язок цього рівняння x. а, b , k − існує для будь-якого a ∈ R (k ≠ 0 за умовою). Таким чином, значенням заданої функції може бути будь-яке дійсне число, отже, її область значень E (f) = R. Позначимо значення заданої функції f (x) (тобто kx + b) через a і з’ясуємо, для яких a можна знайти відповідне значення x, таке, що f (x) = a. Множина всіх таких значень a і буде складати область значень функції f (x).

Перетворення графіків функцій Перетворення вздовж осі ординат Y = k F (x) А) k > 0 – розтягування вздовж осі ординат Y k разів Б) 0 < k < 1 – стискання вздовж осі ординат Y разів В) k = - 1 – симетричне відображення відносно осі абсцис

Перетворення вздовж осі ординат Y = F (x) + b Паралельне перенесення осі ординат на І b І одиниць: А) вгору, якщо b > 0; Б) вниз, якщо b < 0

Перетворення вздовж осі ординат Y = І F (x) І Збереження частин графіка, які лежать над віссю Ох і симетричне відображення відносно осі Ох тих частин графіка, які розташовані нижче від осі Ох.

Перетворення вздовж осі абсцис Паралельне перенесення вздовж осі абсцис на І одиниць: Y = F (x + a) А) ліворуч, якщо а > 0; Б) праворуч, якщо а < 0

Перетворення вздовж осі абсцис Y=F(nx) А) n > 0 – стискання вздовж осі абсцис у n разів Б) 0 < n < 1 – розтягування вздовж осі абсцис у разів В) n = - 1 – симетричне відображення відносно осі ординат

Перетворення вздовж осі абсцис Y=FІxІ Відкидання частин графіка, які лежать ліворуч від осі Оу і збереження та відображення симетрично осі Оу тих частин графіка, які розташовані у правій напівплощині

Математичний термін функція вперше з’явився в 1692 р у Лейбніца, як зв’язок різних відрізків з довільною кривою

Початкове поняття функції, як функціональну залежність та її графічне зображення ввів Ферма.

Перше загальне визначення функції зустрічається у Іоанна Бернуллі (1718 р).

Сучасне визначення числової функції, як довільної відповідності чисел вводе Ейлер (1755 р)

Література 1. Мерзляк А. Г. , Номіровський Д. А. , Полонський В. Б. , Якір М. С. Алгебра і початки аналізу. (Академічний рівень) 10 клас. - Х. : Гімназія, 2010. 2. Нелін Є. П. Алгебра і початки аналізу. (Академічний рівень) 10 клас. - Х. : Гімназія, 2010. 3. Бевз Г. П. Алгебра. (Академічний рівень)10 клас. – Х. : Гімназія, 2010

Інтернет ресурси http: //formula. co. ua http: //college. ru http: //wikipedia. org