Функциональные ряды Продолжение Лекция 21 Вычисление

Функциональные ряды. Продолжение Лекция № 21

Вычисление определенных интегралов с помощью рядов 2

Решение дифференциальных уравнений с помощью рядов 3

Тригонометрические ряды Периодическая кусочно-гладкая функция описывается не степенным, а тригонометрическим рядом. Периодическая кусочно-гладкая функция – определена и непрерывна на всей оси, за исключением заданных точек, в которых она терпит разрыв первого рода, и удовлетворяет равенству: Пример 1. Построить график периодической функции с периодом T = 2 4

Задача: Если f(x) и F(x) периодические Ряд Фурье Любая кусочно-гладкая периодическая функция с периодом равным 2 представляется в виде сходящегося тригонометрического ряда: 5

Ортогональность системы тригонометрических функций Интеграл по отрезку [- , ] от произведения двух любых функций, входящих в ряд Фурье равен: • нулю, если в подынтегральную функцию входят различные функции системы • положительному числу, если подынтегральная функция состоит из квадрата любой функции системы 6

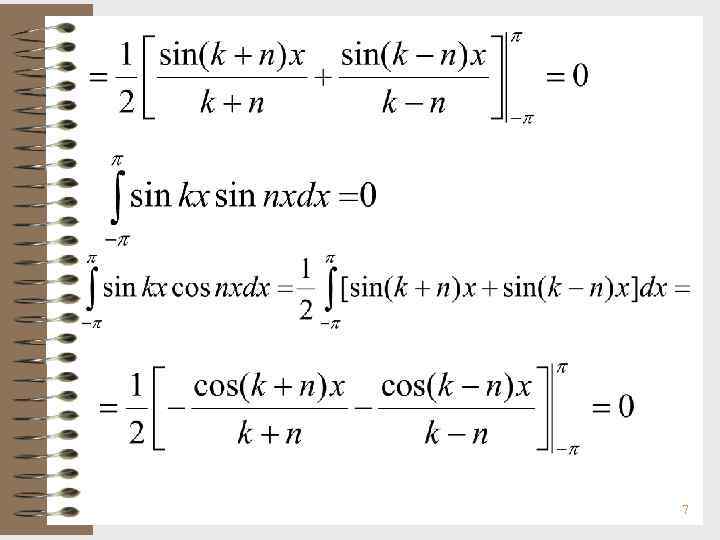7

Для определения коэффициентов разложения периодической функции в ряд Фурье воспользуемся методом Эйлера – Фурье: последовательно умножаем обе части разложения на cos nx, sin nx и интегрируем 8

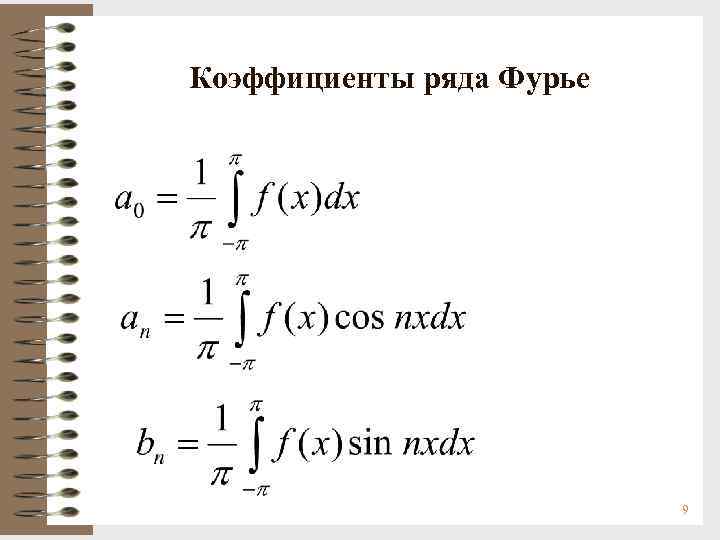Коэффициенты ряда Фурье 9

Сходимость ряда Фурье Теорема. Пусть функция непрерывна вместе со своей производной на отрезке [- , ] или они имеют на этом отрезке конечное число точек разрыва. Тогда: • ряд Фурье сходится на все числовой прямой. • в каждой точке непрерывности f(x) на интервале [- , ] сумма ряда равна значению функции f(x) в этой точке. • в каждой точке разрыва сумма ряда равна полусумме односторонних пределов: 10

• на концах отрезка [- , ] сумма ряда равна • для любой точки вне отрезка [- , ] предыдущие утверждения справедливы для периодического продолжения функции f(x) 11

Ряды Фурье для четных и нечетных функций f(x) – нечетная f(x) – четная 12