Скачать презентацию Функциональное программирование III Представление данных в простом нетипизированном
FP III (Programming with Lambda).pptx
- Количество слайдов: 35
Функциональное программирование III Представление данных в простом нетипизированном -исчислении. -исчисление как язык программирования.
Логические значения и операции •
•
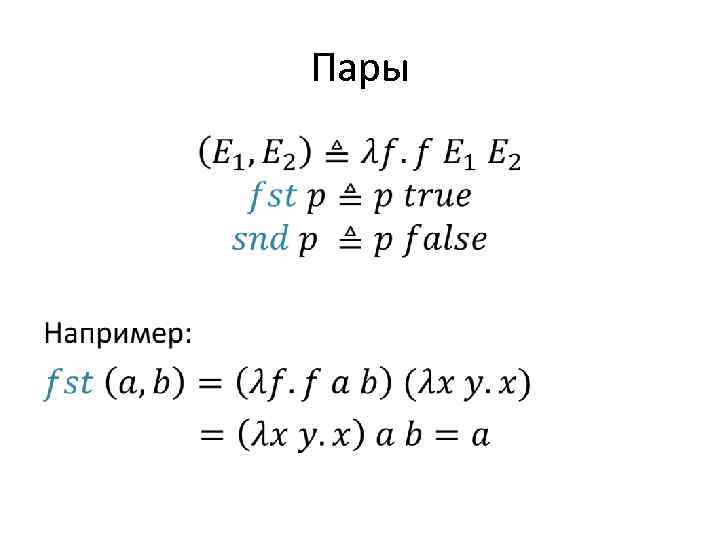Пары •
•
Кортежи •
•
•
Church Numerals •
•
•
•
•
•
Рекурсия — это единственный метод выражения итерации в лямбда-исчислении. Тем не менее, кажется, что для выражения рекурсии необходимо именовать рекурсивные функции. К счастью, благодаря усилиям Карри был найден метод создавать анонимные рекурсивные функции.
•
•
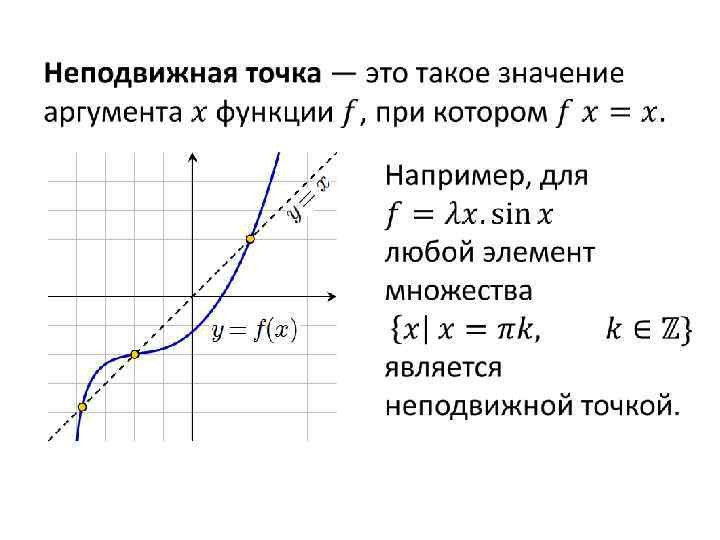Парадокс Рассела •
•
•
•
•
•
Let bindings •
•
•
•
•
•
•
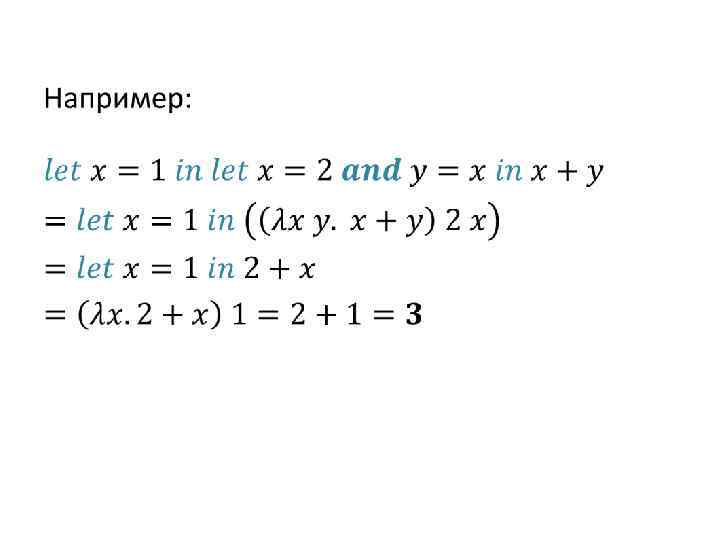Без «сахара» : (λf. (λx. f (x x))) (λf n. ((n (λx y. y)) (λx y. x) ((λf x. (n ((λf p. (λf. f (λx y. y)((p (λx y. x)) (p (λx y. y)) (f (p (λx y. y)))))) f)(λf. f (λ x y. x) x))(λx y. y)) (λx y. x))) (λf x. f x) (λg x. (f (λf x. (n ((λf p. (λf. f (λx y. y)((p (λx y. x)) (p (λx y. y)) (f (p (λx y. y)))))) f)(λf. f (λ x y. x) x))(λx y. y))) g ((f ((λf x. f (f x)) (λn f x. (n ((λf p. (λf. f (λx y. y)((p (λx y. x)) (p (λx y. y)) (f (p (λx y. y)))))) f) (λf. f (λ x y. x) x)) (λx y. y)) n)) g x)))
•
Полнота по Тьюрингу Таким образом мы видим, что уже на этом этапе мы можем записать многие программы, в том числе — рекурсивные. Нетипизированное лямбда-исчисление полно по Тьюрингу — на нём можно записать любую вычислимую функцию. Полное доказательство смотрите в: Gordon (1988) “Programming Language Theory and its implementation. Applicative and imperative paradigms”
Примечание •
Дополнительная информация по теме: Ø John Harrison “Introduction to functional programming” Ø Achim Jung “A short introduction to the Lambda Calculus” Ø Pierce “Types and Programming Languages” Ø Hindley, Seldin “Lambda-Calculus and Combinators, an Introduction” Ø Simmons, Schalk “An Introduction to lambdacalculus and arithmetic with a decent selection of exercises”