Скачать презентацию Функциональное программирование II Нетипизированное -исчисление Порядки редукции
FP II (Lambda calculus).pptx
- Количество слайдов: 58
Функциональное программирование II Нетипизированное -исчисление. Порядки редукции.
Лямбда-исчисление Проследим историю развития математики: — Запись чисел появилась около 1200 ых годов — Нотация для записи выражений и уравнений появилась в 17 ом веке — И только в 1930 ых появилась нотация для записи функций. Эта нотация была изобретена Чёрчем и называется лямбда-исчислением.
Лямбда-исчисление — это формальная система, нотация для записи функция. Формальная система — это формальный язык (множество термов) и правила вывода. Формальные системы не имеют семантики, это просто набор синтаксических правил.
Все операторы — префиксные. Т. е. вместо: 2 + 3 мы запишем: + 2 3. sin(x) sin x sin(x) + 5 + (sin x) 5 sin(x) + cos(x) + (sin x) (cos x) 2 + 5(ln(x) + sin(x)) + 2 (* 5 (+ (ln x) (sin x)))
•
Теперь мы можем создавать функции, не указывая их имена. Некоторые языки программирования также поддерживают похожую нотацию. Сравните: Lambda Calculus Lisp (lambda (x) (+ x 3)) F# fun x -> x + 3 C# x => x + 3 Haskell
•
•
•
Задание #2 •
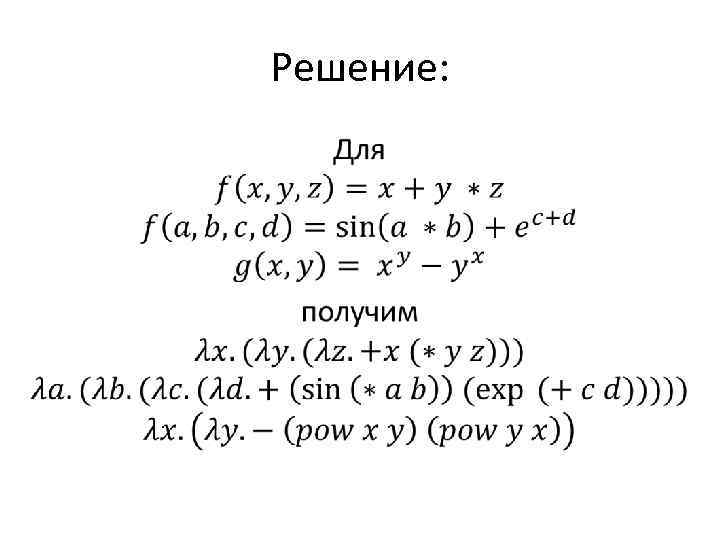Решение: •
•
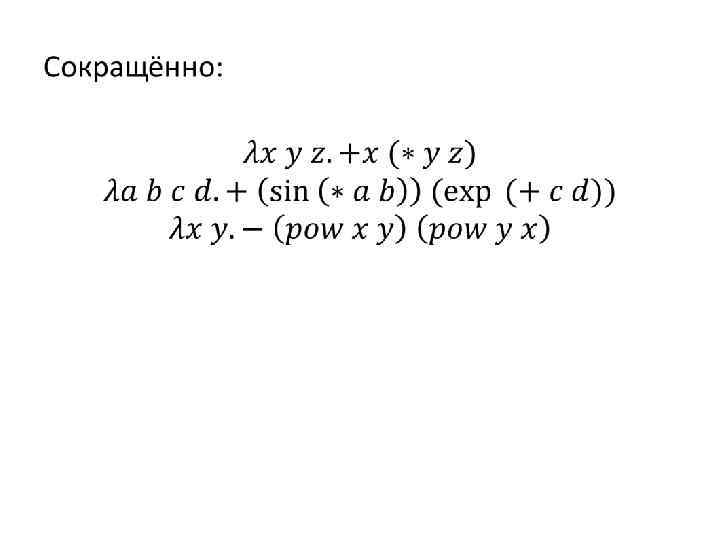Преимущества лямбда-нотации •
Связанные/свободные переменные •
•
•
•
•
•
Задание #3 •
Решение •
Подстановка •
Наивная формализация подстановки •
•
Capture-avoiding substitution •
Задание #4 •
Решение •
Редукции •
•
•
•
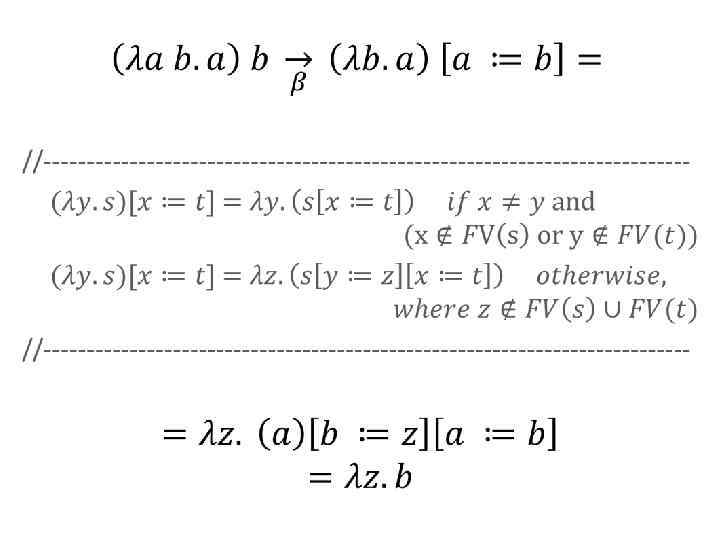//reflexivity //symmetry //transitivity //substitutivity
•
•
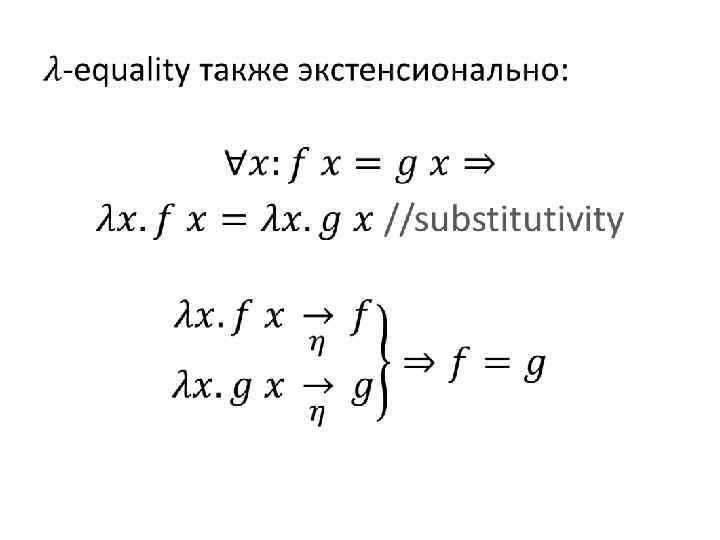Специальные равенства •
•
Нормальная форма •
•
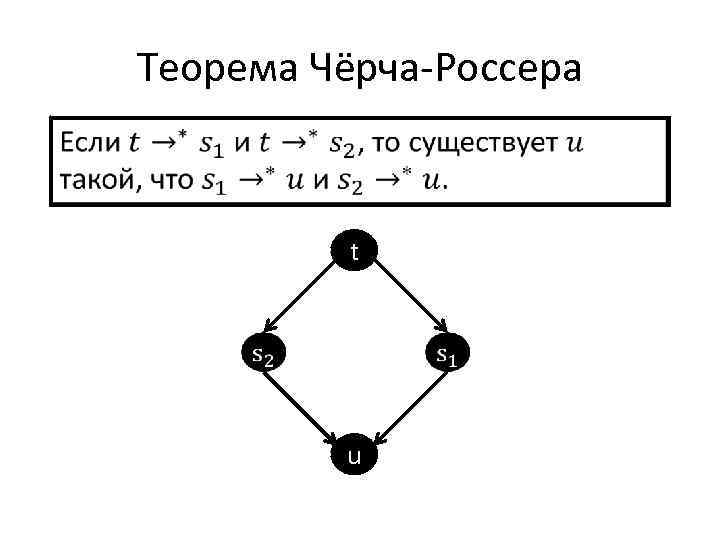Теорема Чёрча-Россера t u
•
•
Задание #5 •
Ответы 5 •
Evaluation strategy •
•
•
Normal order Нормальный порядок редукции — это такой порядок, при котором на каждом шаге редуцируется самый левый самый внешний редекс. В нашем примере таким редексом был редекс 1.
Самый левый самый внешний редекс: Нормальный порядок всегда доходит до нормальной формы, если она есть.
•
Call by Name •
•
•
Call by Need — то же, что call by name, но мемоизует результаты вычислений, поэтому в предыдущем примере 200! будет посчитан только один раз. Использует Abstract Syntax Graph вместо Abstract Syntax Tree.
Applicative order •
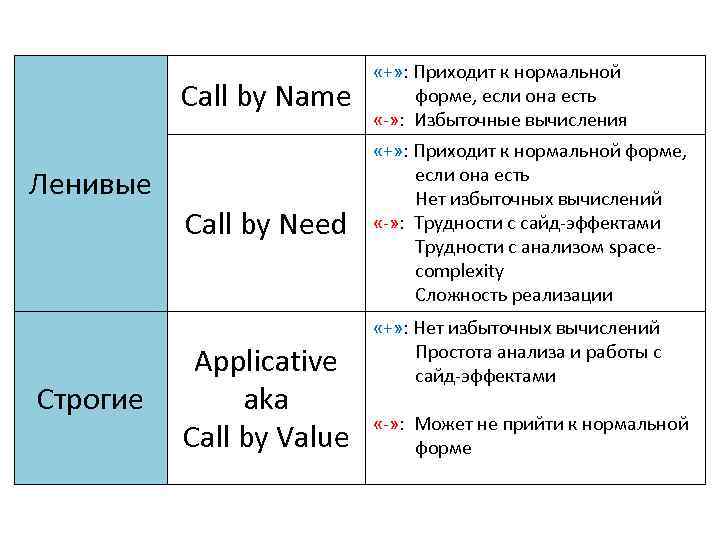Call by Name «+» : Приходит к нормальной форме, если она есть «-» : Избыточные вычисления Call by Need «+» : Приходит к нормальной форме, если она есть Нет избыточных вычислений «-» : Трудности с сайд-эффектами Трудности с анализом spacecomplexity Сложность реализации Ленивые Строгие Applicative aka Call by Value «+» : Нет избыточных вычислений Простота анализа и работы с сайд-эффектами «-» : Может не прийти к нормальной форме
Кроме того, ленивые вычисления обычно медленнее, тем не менее, строгие будут считать значения аргументов, даже если они не будут использованы функцией. Отсутствие гарантии нахождения нормальной формы для строгих вычислений на практике не является помехой для их применения.
Call by Value Call by Need Call by Name C, C++, C#, F#, Java, OCaml, Python, Ruby, Perl, Pascal, Delphi, . . . Haskell, R, . Net с помощью Lazy
Тем не менее, условное выражение всегда вычисляется лениво. Действительно, if x <> 0 then y / x else 0 не приведёт к делению на нуль.