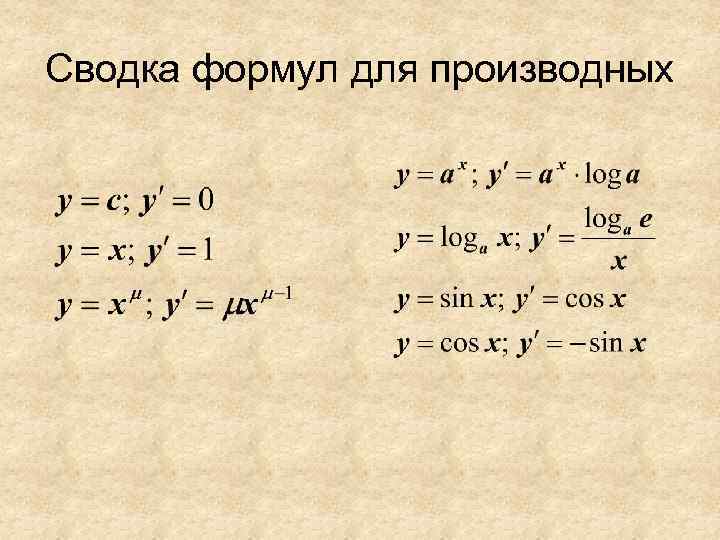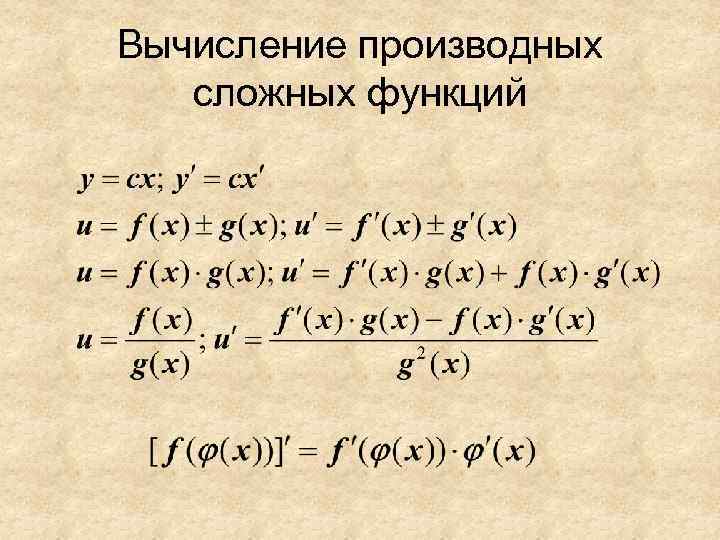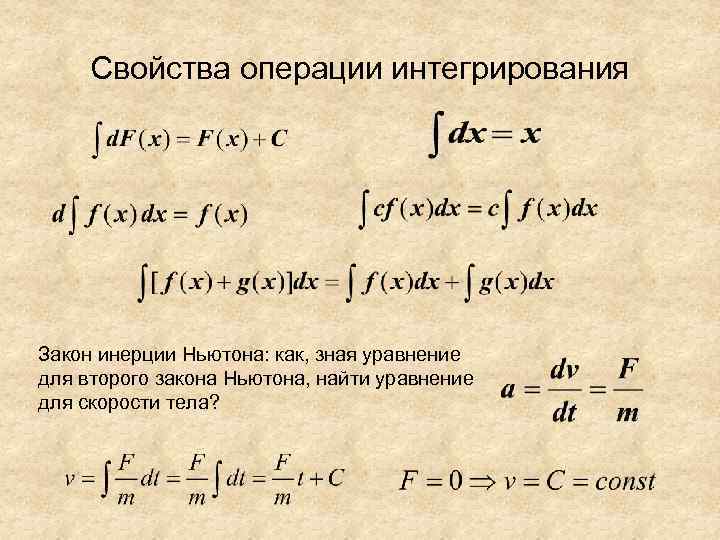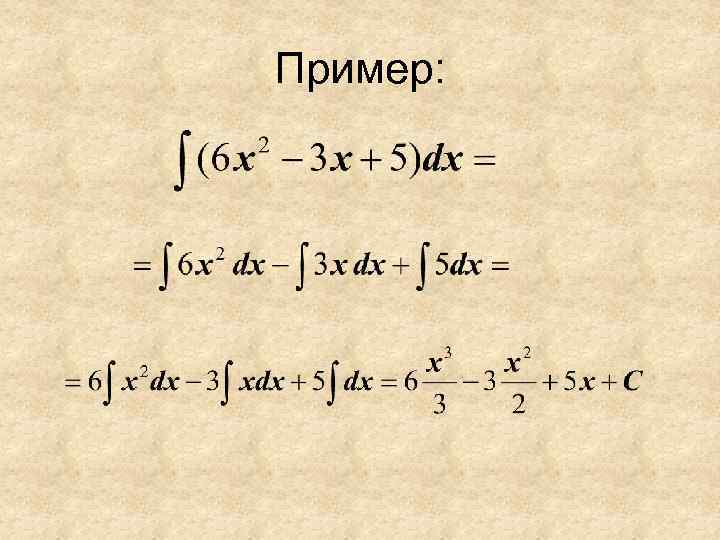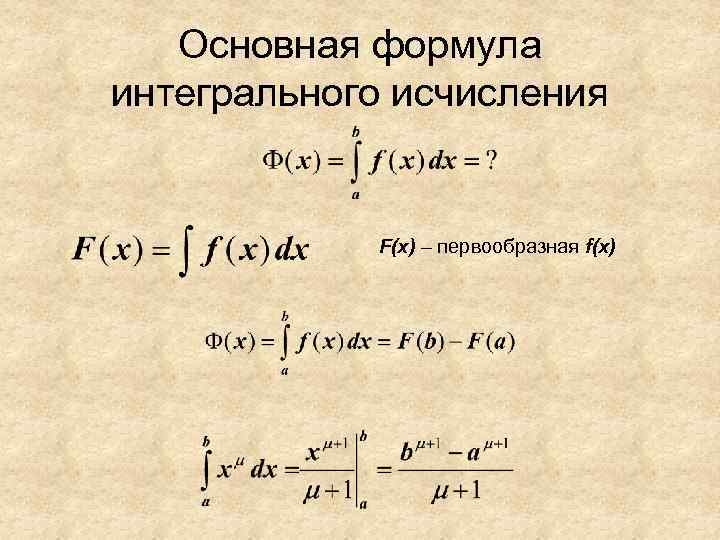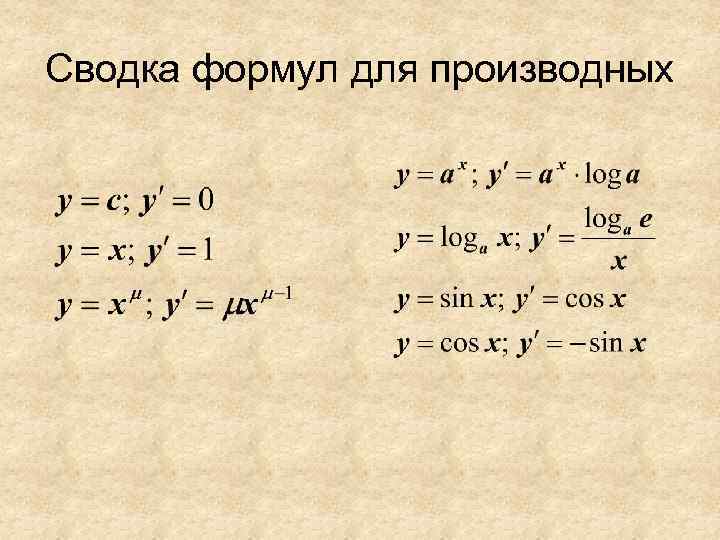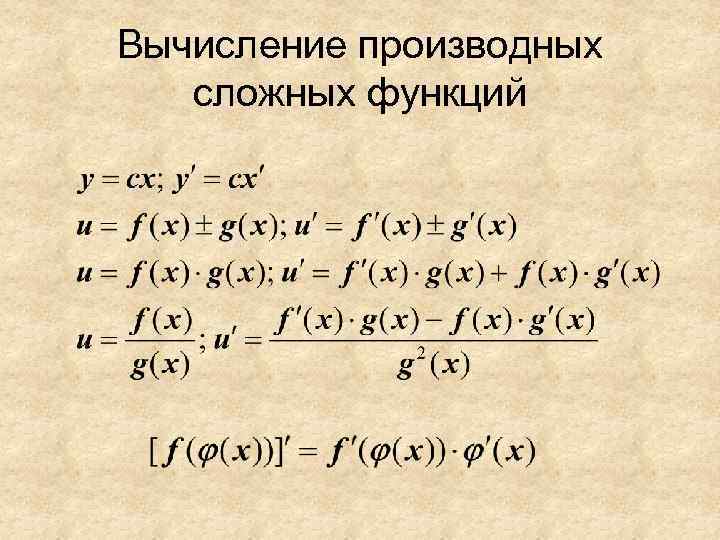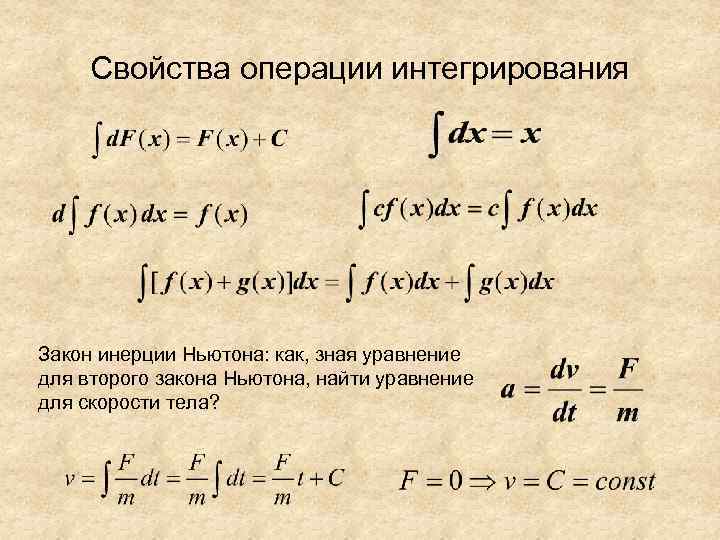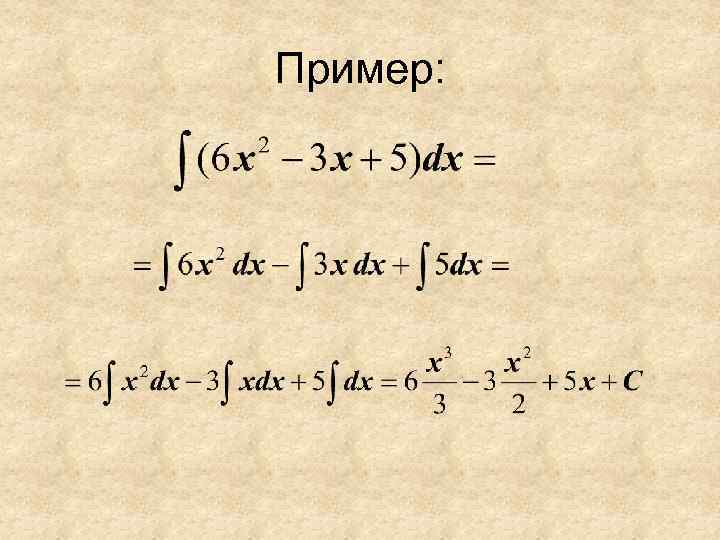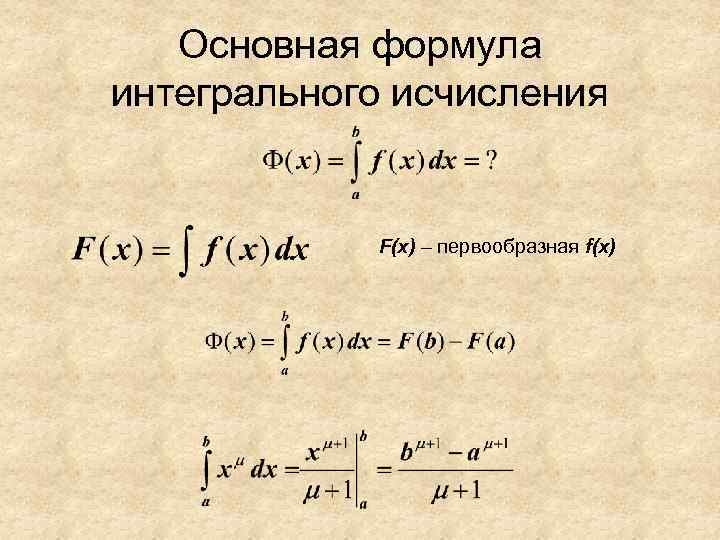Функции, производные, интегралы

Функции, производные, интегралы

Определение функции Переменная y называется функцией от переменной х в области ее изменения Х, если по некоторому правилу (закону) каждому значению х из Х ставится в соответствие одно или несколько определенных значений y

Способы задания функции 1. Табличный (подходит для дискретных функций); 2. Аналитический (выражается формулой) 3. Графический (выражается графиком на плоскости)

Определение производной функции Свободное падение тела в пустоте

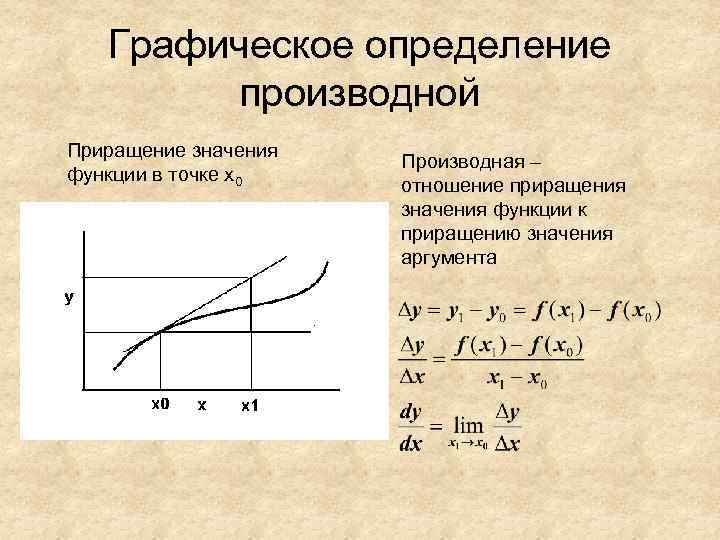Графическое определение производной Приращение значения Производная – функции в точке х0 отношение приращения значения функции к приращению значения аргумента

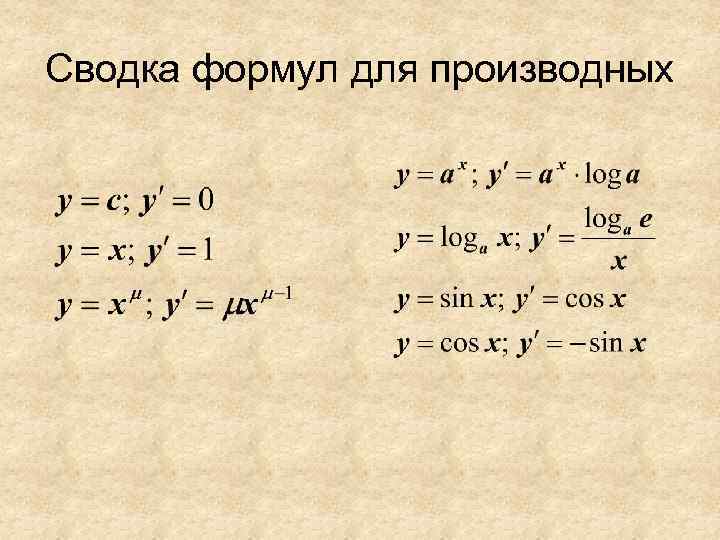Сводка формул для производных

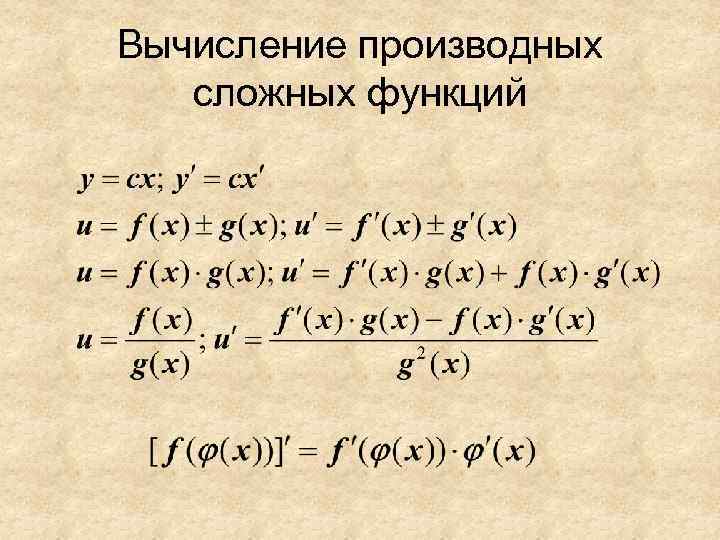Вычисление производных сложных функций

Производные более высоких порядков Если первая производная функции – скорость изменения функции, то вторая производная – ускорение (скорость изменения скорости)

Анализ поведения функции Наибольшие и наименьшие значения функции Пределы значений функции Непрерывность и разрывы функций Нули и полюса функций

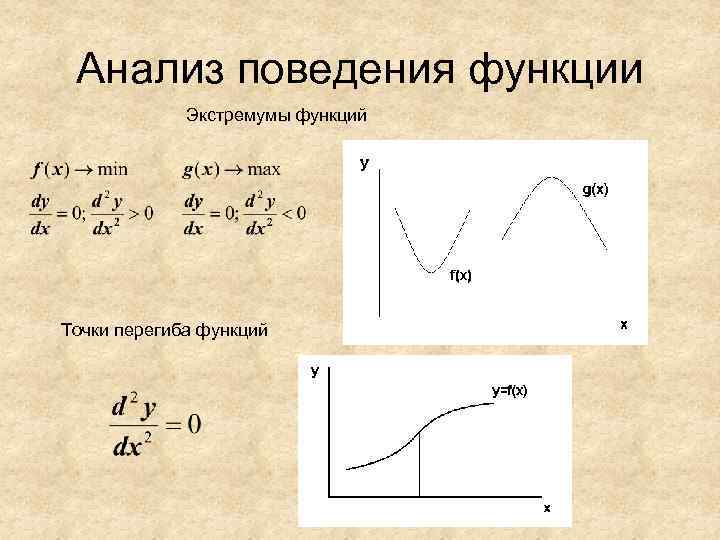Анализ поведения функции Экстремумы функций Точки перегиба функций

Правило нахождения экстремума

Перегибы, выпуклость и вогнутость функции Если вторая производная в точке М больше нуля, то кривая в той точке вогнутостью направлена вверх. Если вторая производная в точке М меньше нуля, то кривая в той точке вогнутостью направлена вниз. Если вторая производная в точке М равна нулю, то М – точка перегиба

Первообразная функции дифференцирование: известно уравнение движения s=s(t); найти скорость v=ds/dt и ускорение dv/dt интегрирование: задана функция ускорения a=a(t), требуется определить скорость v и пройденный путь s Функция F(x) называется первообразной функцией для функции f(x) или интегралом от f(x), если f(x) является производной для функции F(x), или, что то же самое, f(x)dx служит для F(x) дифференциалом.

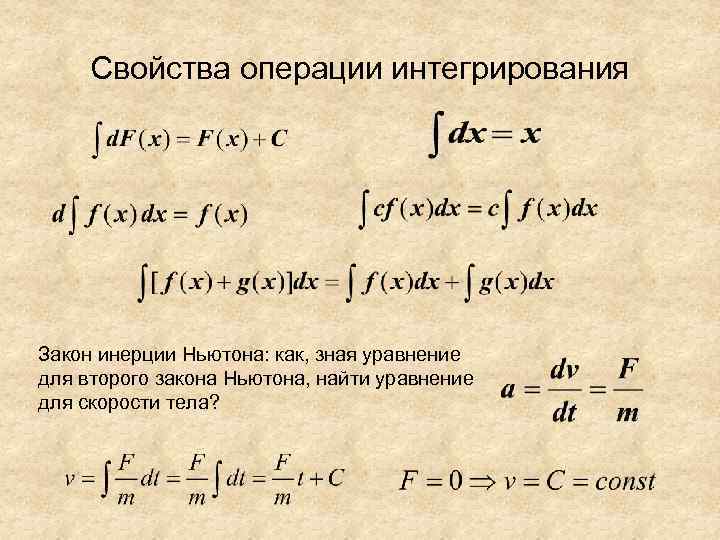Свойства операции интегрирования Закон инерции Ньютона: как, зная уравнение для второго закона Ньютона, найти уравнение для скорости тела?

Таблица интегралов основных функций

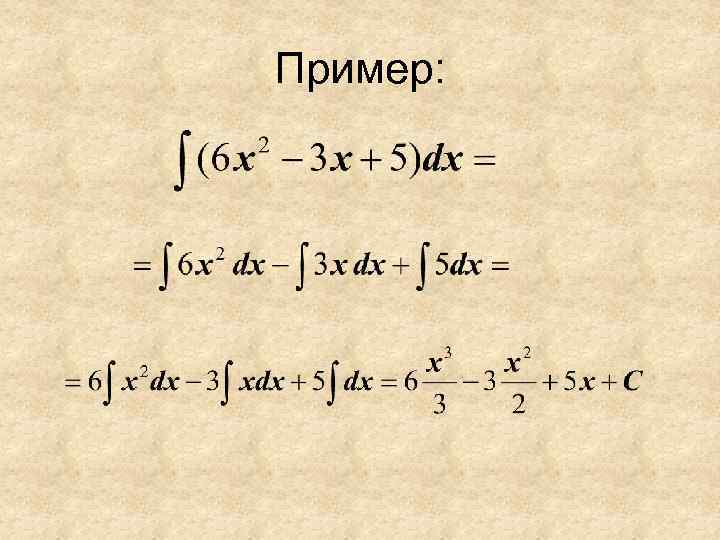Пример:

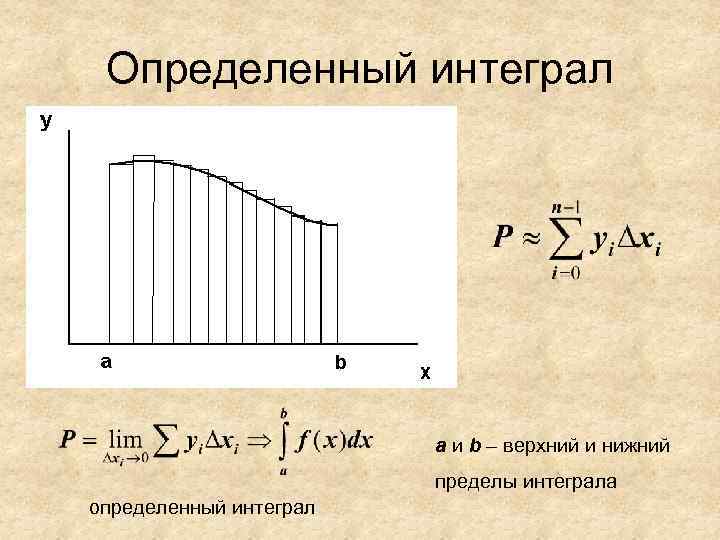Определенный интеграл a и b – верхний и нижний пределы интеграла определенный интеграл

Свойства определенного интеграла

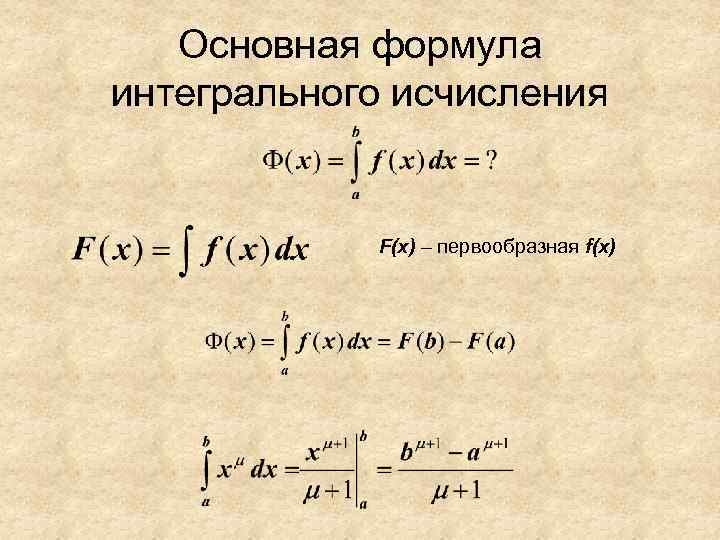Основная формула интегрального исчисления F(x) – первообразная f(x)

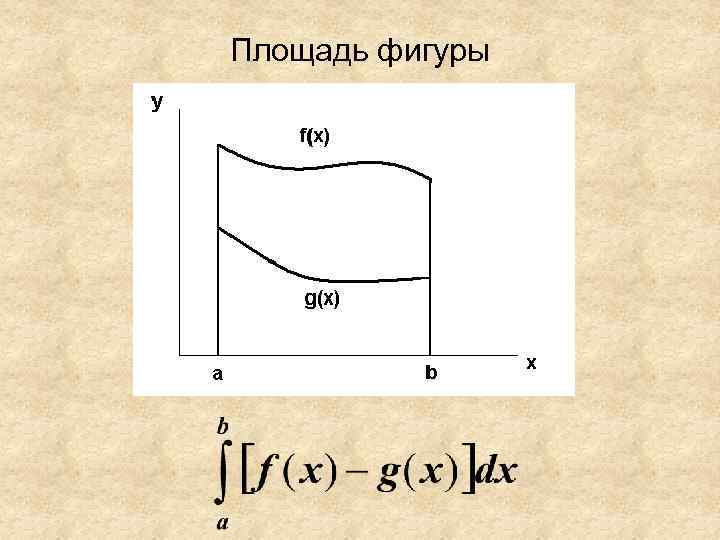Площадь фигуры