Функции для работы с массивами в Matlab

• Различные способы ввода матриц в пакете Mat. Lab » А = [3 1 -1; 2 4 3] А = 3 1 -1 2 4 3 » В = [4 3 -1 2 7 0 -5 1 2] B = 4 3 -1 2 7 0 -5 1 2 » С = [[3; 4] [-1; 2] [7; 0]] С = 3 -1 7 4 2 0 2

Посмотрите переменные рабочей среды, набрав в командной строке whos: А 2 x 3 48 double array В 3 x 3 72 double array С 2 x 3 48 double array 3

Удаление строк и столбцов • В Mat. Lab парные квадратные скобки [ ] обозначают пустой массив, который, в частности, позволяет удалять строки и столбцы матрицы. » М = [2 0 3 1 1 4 6 1 3]; » M(1, : )=[ ]; » M M = 1 1 4 6 1 3 » size(M) ans = 2 3 Аналогичным образом удаляются и столбцы. » М(: , 2: 3) = [ ] M = 1 6

5

Создание матриц специального вида • Для работы с матрицами удобно пользоваться следующими функциями q ones – формирование массива из единиц q zeros – формирование массива из нулей q eye – формирование единичной матрицы q rand – формирование массива из чисел, случайно распределённых на отрезке [0, 1] q randn – формирование массива из чисел, нормально распределённых на отрезке [0, 1] q magic – формирование магического квадрата q pascal – формирование квадрата Паскаля q diag – диагональная матрица q и др. 6

Матрицы специального вида • Рассмотрим основной синтаксис на примере функции создания единичной матрицы (eye) • eye(m) – создание единичной матрицы размера [m, m] • eye(m, n) – создание единичной матрицы размера [m, n] – «лишние» строки или столбцы дополняются нулями 7

Матрицы специального вида 8

Матрицы специального вида 9

Матрицы специального вида 10

Матрицы специального вида 11

Матрицы специального вида • Функция diag: работа с диагональными матрицами – у которых ненулевые элементы расположены на диагоналях • Синтаксис: – X = diag(v) – на главной диагонали матрицы X расположены элементы вектора v – X = diag(v, k) – на k-ой диагонали матрицы X расположены элементы вектора v (по умолчанию k=0) – v = diag(X, k) – извлечь из матрицы X k-ую диагональ и сохранить её в векторе v 12

Матрицы специального вида 13

Матрицы специального вида 14

Вычисления с элементами массивов • Простейшие операции над элементами массивов: – sum: сумма элементов – prod: произведение элементов – max: нахождение максимального элемента – min: нахождение минимального элемента – sort: сортировка элементов 15

Вычисления с элементами массивов • Рассмотрим работу некоторых из этих функций на примере sum • Для векторов эта функция возвращает сумму элементов • Для массивов – сумму элементов по каждому из столбцов – результат – вектор-строка • Остальные функции работают по этому же принципу 16

Вычисления с элементами массивов 17

Вычисления с элементами массивов • Максимальный и минимальный элементы: 18

Вычисления с элементами массивов • Вызов функций max/min с двумя выходными параметрами позволяет определить и индекс найденного элемента: 19

Вычисления с элементами массивов • Функция sort производит сортировку элементов матрицы по столбцам: 20

Поиск в массиве • find: определяет индексы элементов, удовлетворяющих заданному условию 21

Поиск в массиве • Пример применения команды find к массивам: 22

Математические матричные операции • det – вычисление определителя квадратной матрицы 23

Матричные и поэлементные операции • При работе с матрицами можно использовать два вида операторов: – матричные: производят действия по матричные: правилам матричной алгебры – поэлементные: производят действия над поэлементные: соответствующими элементами матриц • размеры матриц должны быть одинаковыми • от матричных операций отличаются точкой перед знаком операции 24

Матричные и поэлементные операции • ‘ транспонирование • матричное деление • + матричное (и «слева» поэлементное) • . * поэлементное сложение умножение • - матричное (и • . / поэлементное) деление вычитание • . ^ поэлементное • * матричное умножение возведение в степень • / матричное деление • . поэлементное • ^ матричное деление «слева» возведение в степень 25

Матричные и поэлементные операции 26

Матричные и поэлементные операции • Такие операции часто используются, если нужно применить какую либо функцию ко всем элементам матрицы. 27

Матричные и поэлементные операции • Некоторые операции по умолчанию считаются поэлементными: 28

Операции «деления» слева и справа • Применяются для решения систем линейных уравнений (СЛУ) • Деление слева () – для квадратных матриц реализует метод Гаусса – для прямоугольных матриц – метод наименьших квадратов 29

Заполнение матриц при помощи индексации Генерация матрицы Т осуществляется в три этапа: • 1. Создание массива T размера пять на пять, состоящего из нулей. • 2. Заполнение первой строки единицами. • 3. Заполнение части последней строки минус единицами до последнего элемента. 30

» A(1: 5, 1: 5) = 0 A= 0 0 0 0 0 0 0 » A(1, : ) = 1 A= 1 1 1 0 0 0 0 0 » A(end, 3: end) = -1 A= 1 1 1 0 0 0 0 0 -1 -1 -1 31

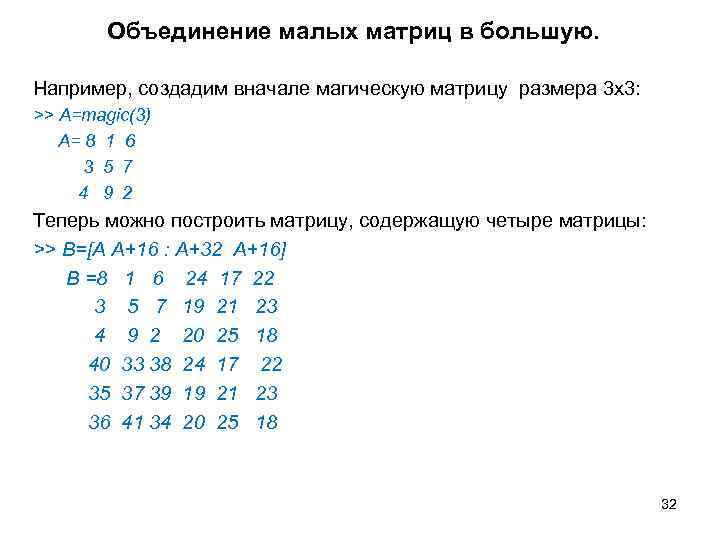
Объединение малых матриц в большую. Например, создадим вначале магическую матрицу размера 3 x 3: >> A=magic(3) А= 8 1 6 3 5 7 4 9 2 Теперь можно построить матрицу, содержащую четыре матрицы: >> В=[А А+16 : А+32 А+16] В =8 1 6 24 17 22 3 5 7 19 21 23 4 9 2 20 25 18 40 33 38 24 17 22 35 37 39 19 21 23 36 41 34 20 25 18 32

Ведение дневника. Загрузка рабочей области сессии. • diary filename – ведет запись на диск всех команд в строках ввода и полученных результатов в виде текстового файла с указанным именем; • diary off – приостанавливает запись в файл; • diary on – вновь начинает запись в файл. Таким образом, чередуя команды diary off и diary on, можно сохранять нужные фрагменты сессии в их формальном виде. Команду diary можно задать и в виде функции diary('file'), где строка 'file' задает имя файла. Например: >> diary myfile. m >> 1+2 ans = 3 >> diary off >> 2+3 ans = 5 >> diary on sin(l) ans = 0. 8415 33 >> diary off