Функції АКТУАЛЬНІСТЬ РОЗРОБЛЕНОЇ ТЕМИ Функції це

Функції

АКТУАЛЬНІСТЬ РОЗРОБЛЕНОЇ ТЕМИ: Функції – це одна з основних і найскладніших тем математики. Важко назвати якийсь розділ алгебри чи математичного аналізу, де б ми не мали справу з функціями, їх властивостями. Тому досконале знання цієї теми – один з найуспішніших кроків при підготовці до ЗНО. Крім того, немає жодної галузі людського знання куди б не входило поняття про функції та їх графічне зображення. Функція – зручна модель для дослідження багатьох процесів. Для того, щоб дослідити процеси і явища навколишнього світу, слід спочатку навчитися встановлювати характерні особливості відповідних математичних моделей. Перед усім це стосується функцій.

МЕТА НАУКОВО-ДОСЛІДНИЦЬКОЇ РОБОТИ: Досконале вивчення функції при різних способах її задання, детальне дослідження всіх її властивостей та застосування цих знань при дослідженні та побудові графіків функцій.

ЗАВДАННЯ: v З’ясувати основні способи задання функцій. v Детально проаналізувати кожну властивість функції. v Розглянути дослідження й побудову графіків на прикладі тригонометричних функцій, побудова цілої і дробової частини.

Функції. Властивості функцій. Графіки функцій. Функції, задані формулою.

Робота складається з п’яти основних розділів. В першому коротко розглянута історія розвитку поняття функції, в другому – сталі та змінні величини і показаний перехід до поняття функціональної залежності, в третьому – способи задання функції. Четвертий розділ присвячений властивостям функцій, які детально описані та дослідженні, і показано їх практичне застосування. У п’ятому розділі за загальною схемою проведено дослідження тригонометричних функцій, цілої та дробової частини числа, побудовано їх графіки. Розглянуто основні перетворення графіків функцій.

Означення функції, яким ми користуємось на даному етапі вивчення математики, з’явилося порівняно недавно – у першій половині XIX ст. Воно формувалося більш 200 років під впливом бурхливих суперечок видатних математиків кількох поколінь. Дослідженням функціональних залежностей між величинами почали займатися ще стародавні вчені. Прикладами табличного задання функцій можуть слугувати астрономічні таблиці вавилонян, стародавніх греків і арабів.

Проте лише в першій половині XVII ст. своїм відкриттям методу координат видатні французькі математики П. Ферма і Р. Декарт заклали основи для виникнення поняття функції. Значну роль у формуванні цього поняття відіграли роботи великого англійського вченого Ісаака Ньютона. Під функцією він розумів величину, яка змінює своє значення з плином часу.

П’єр Ферма Рене Декарт Ісаак Ньютон

Георг Лейбніц і його учень швейцарський математик Йоганн Бернуллі під функцією розуміли формулу, яка пов’язую одну змінну з іншою, тобто вони ототожнювали функцію з одним із способів її задання. Подальшому розвиткові поняття функції багато в чому сприяло з’ясування істини в багаторічному спорі видатних математиків Леонарда Ейлера і Жана Лерона Д’Аламбера. У результаті було сформовано більш загальний погляд на функцію як залежність однієї змінної величини від іншої, у якому це поняття жорстко не пов’язувалося зі способом задання функції.

Георг Лейбніц Йоганн Бернуллі

Леонард Ейлер Жан Лерон Д’Аламбер

У 30 -х роках XIX ст. ідеї Ейлера набули подальшого розвитку в роботах видатних учених: російського математика Миколи Лобачевського і німецького математика Петера Діріхле. Саме тоді з’явилося таке означення: змінну величину у називають функцією змінної величини х, якщо кожному значенню величини х відповідає єдине значення величини у. Коли на межі XIX і XX століть виникла теорія множин і стало зрозумілим, що елементами області визначення і області значень зовсім не обов’зково мають бути числа, то під функцією стали розуміти правило, яке кожному елементу множини Х ставить у відповідність єдиний елемент множини Y.

Микола Лобачевський Петер Діріхле

ØАналітичний спосіб. ØГрафічний спосіб. ØТабличний спосіб. ØСловесний спосіб

Властивості функції 1) Знайти області визначення і значень даної функції f. 2) З'ясувати, чи має функція особливості, що полегшують дослідження, тобто чи є функція f: а) парною чи непарною; б) періодичною. 3) Обчислити координати точок перетину графіка з осями координат. 4) Знайти проміжки знакосталості функції f. 5) З'ясувати, на яких проміжках функція f зростає, а на яких спадає. 6) Знайти точки екстремума, вид екстремума (максимум чи мінімум) і обчислити значення f у цих точках. 7) Вияснити, чи має функція вертикальні, горизонтальні та похилі асимптоти.

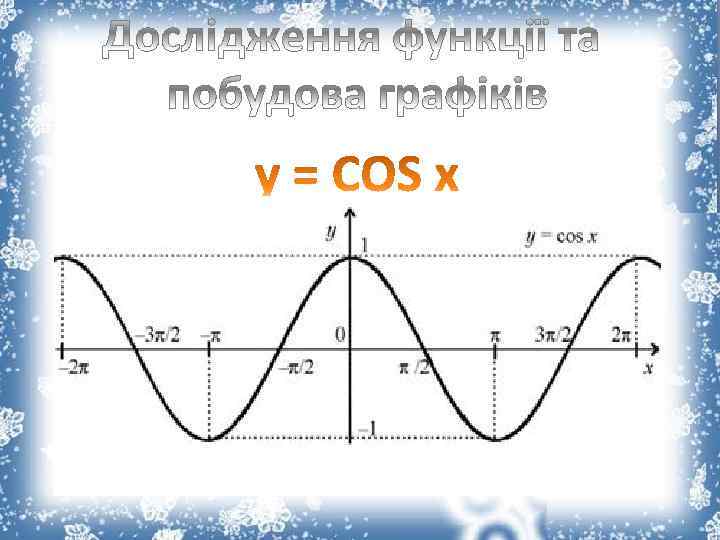
1) D(x) = R. E(y) = [-1; +1]. 2) a) Парна, f(-x) = f(x). б) Періодична, T = 2∏. 3) x = 0, y = 1. y = 0, x = ∏/2 + ∏n, n є Z. 4) y > 0, x є (- ∏/2 + 2∏n; ∏/2 + 2∏n), n є Z. y < 0, x є (∏/2 + 2∏n; 3∏/2 + 2 ∏n), n є Z. 5) Зростає (- ∏ + 2∏n; 0 + 2 ∏n), n є Z. Спадає (0 + 2 ∏n; ∏ + 2∏n), n є Z. 6) max y(x) = 0 + 2∏n, n є Z. 7) min y(x) = (∏ + 2∏n), n є Z.

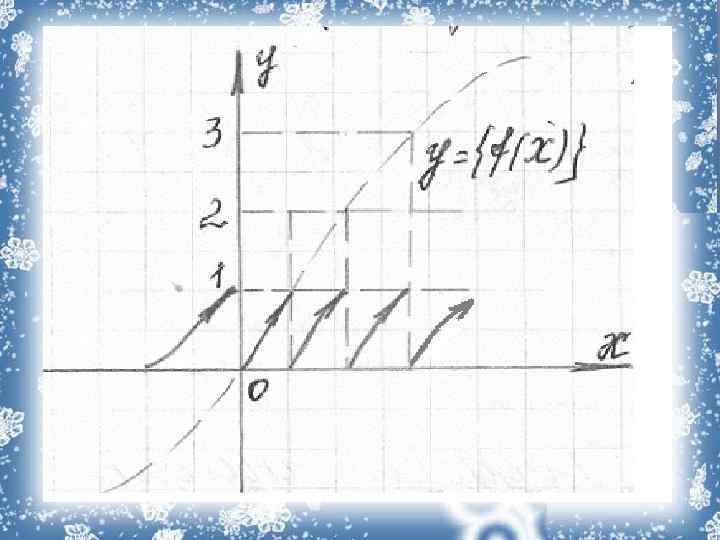
Для побудови графіків виду y = {f(x)} розбиваємо координатну площину з побудованим в ній допоміжним графіком y = f(x) на горизонтальні смуги прямими y = n (n є Z). Через точки перетину проведених прямих з графіком, функцій y = f(x) проводимо ще одну серію прямих, паралельних осі ОУ. Ті частини графіка, що попали в утворені прямокутники, будуть відповідати шуканому графіку, якщо змістити їх в напрямі осі абсцис на n одиниць з верхньої півплощини та на n+1 – з нижньої.

Я в своїй роботі детально описав кожну властивість функції. Показав на конкретних прикладах, як знаходити область визначення та область значення, перевіряти функцію на парність та непарність і чи є вона періодичною, знаходити точки перетину графіка з осями координат, проміжки знакосталості та монотонності, екстремуми та чи має вона асимптоти. За даною схемою дослідив і побудував графіки тригонометричних функцій. Розглянув схему побудови графіків цілої та дробової частини та різні способи перетворення графіків функцій.

Практичне застосування: На уроках математики, фізики, при підготовці до ЗНО, районних та обласних олімпіадах.

Теоретико-методологічна база дослідження: Праці Мерзляка А. Г. , Полонського В. Б. , Якіра М. С. Нелін Є. П. , Колмогорова А. Н.

Під час виконання даної роботи я закріпив і поглибив теоретичні знання з основних проблем цієї навчальної дисципліни. З’ясував свій рівень теоретичної підготовки, вміння самостійно і творчо працювати з науковою літературою, правильно аналізувати, тлумачити і застосовувати вивчений матеріал. Над даною темою я планую працювати далі. Зокрема вивчати обернені тригонометричні функції та застосування їх властивостей при розв’язуванні тригонометричних рівнянь та нерівностей. Більш детально познайомлюсь із застосуванням функцій при вивченні інших предметів (біології, хімії, фізики, географії) та різних галузях народного господарства.