9c9c05dee868c4ac02ec72522f4c8b28.ppt
- Количество слайдов: 28
 Fundamentals of Imaging Tao Zhou Chapter 1 Light Source 1. 1 Different kind of light sources and their mechanisms 1. 2 Intensity and color of light sources
Fundamentals of Imaging Tao Zhou Chapter 1 Light Source 1. 1 Different kind of light sources and their mechanisms 1. 2 Intensity and color of light sources
 1. 2. 1 Light Characterization: Intensity and Power Radiometry vs. Photometry Radiometry radiant flux or radiant power is the measure of the total power of electromagnetic radiation (including visible light). Photometry luminous flux or luminous power is the measure of the perceived power of light by human eye.
1. 2. 1 Light Characterization: Intensity and Power Radiometry vs. Photometry Radiometry radiant flux or radiant power is the measure of the total power of electromagnetic radiation (including visible light). Photometry luminous flux or luminous power is the measure of the perceived power of light by human eye.
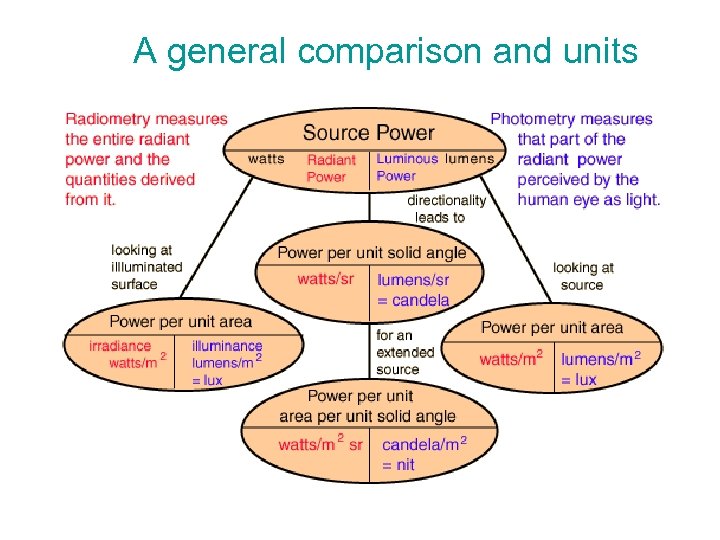 A general comparison and units
A general comparison and units
 Radiant vs. Luminous Power (Flux) The radiant power is the total radiated power in watts, also called radiant flux. This power must be factored by the sensitivity of the human eye to determine luminous flux in lumens. The standard definition is as follows:
Radiant vs. Luminous Power (Flux) The radiant power is the total radiated power in watts, also called radiant flux. This power must be factored by the sensitivity of the human eye to determine luminous flux in lumens. The standard definition is as follows:
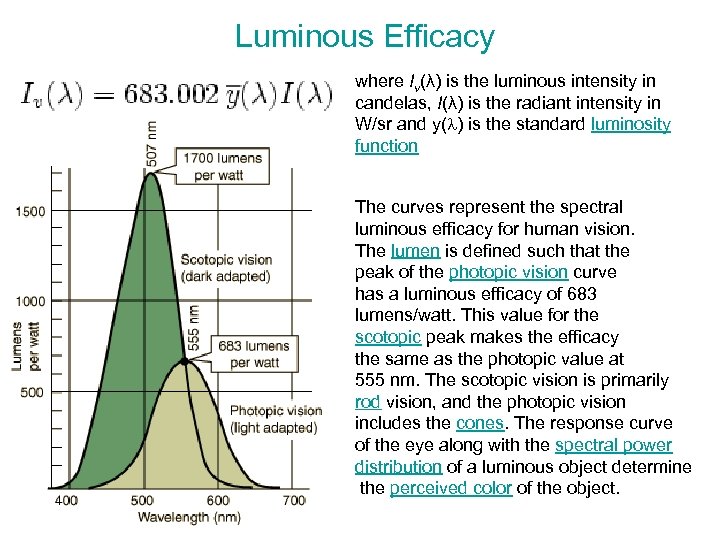 Luminous Efficacy where Iv(λ) is the luminous intensity in candelas, I(λ) is the radiant intensity in W/sr and y(l) is the standard luminosity function The curves represent the spectral luminous efficacy for human vision. The lumen is defined such that the peak of the photopic vision curve has a luminous efficacy of 683 lumens/watt. This value for the scotopic peak makes the efficacy the same as the photopic value at 555 nm. The scotopic vision is primarily rod vision, and the photopic vision includes the cones. The response curve of the eye along with the spectral power distribution of a luminous object determine the perceived color of the object.
Luminous Efficacy where Iv(λ) is the luminous intensity in candelas, I(λ) is the radiant intensity in W/sr and y(l) is the standard luminosity function The curves represent the spectral luminous efficacy for human vision. The lumen is defined such that the peak of the photopic vision curve has a luminous efficacy of 683 lumens/watt. This value for the scotopic peak makes the efficacy the same as the photopic value at 555 nm. The scotopic vision is primarily rod vision, and the photopic vision includes the cones. The response curve of the eye along with the spectral power distribution of a luminous object determine the perceived color of the object.
 Luminous Efficacy Table Wavelength l (nm) Photopic Luminous Efficacy Vl Photopic Conversion lm/W Scotopic Luminous Efficacy Vl Scotopic Conversion lm/W 380 0. 000039 0. 027 0. 000589 1. 001 390 0. 000120 0. 082 0. 002209 3. 755 390 0. 000120 0. 082 0. 002209 3. 755 400 0. 000396 0. 270 0. 009290 15. 793 410 0. 001210 0. 826 0. 034840 59. 228 420 0. 004000 2. 732 0. 096600 164. 220 430 0. 011600 7. 923 0. 199800 339. 660 440 0. 023000 15. 709 0. 328100 557. 770 450 0. 038000 25. 954 0. 455000 773. 500 460 0. 060000 40. 980 0. 567000 963. 900 470 0. 090980 62. 139 0. 676000 1149. 200 480 0. 139020 94. 951 0. 793000 1348. 100 490 0. 208020 142. 078 0. 904000 1536. 800 500 0. 323000 220. 609 0. 982000 1669. 400
Luminous Efficacy Table Wavelength l (nm) Photopic Luminous Efficacy Vl Photopic Conversion lm/W Scotopic Luminous Efficacy Vl Scotopic Conversion lm/W 380 0. 000039 0. 027 0. 000589 1. 001 390 0. 000120 0. 082 0. 002209 3. 755 390 0. 000120 0. 082 0. 002209 3. 755 400 0. 000396 0. 270 0. 009290 15. 793 410 0. 001210 0. 826 0. 034840 59. 228 420 0. 004000 2. 732 0. 096600 164. 220 430 0. 011600 7. 923 0. 199800 339. 660 440 0. 023000 15. 709 0. 328100 557. 770 450 0. 038000 25. 954 0. 455000 773. 500 460 0. 060000 40. 980 0. 567000 963. 900 470 0. 090980 62. 139 0. 676000 1149. 200 480 0. 139020 94. 951 0. 793000 1348. 100 490 0. 208020 142. 078 0. 904000 1536. 800 500 0. 323000 220. 609 0. 982000 1669. 400
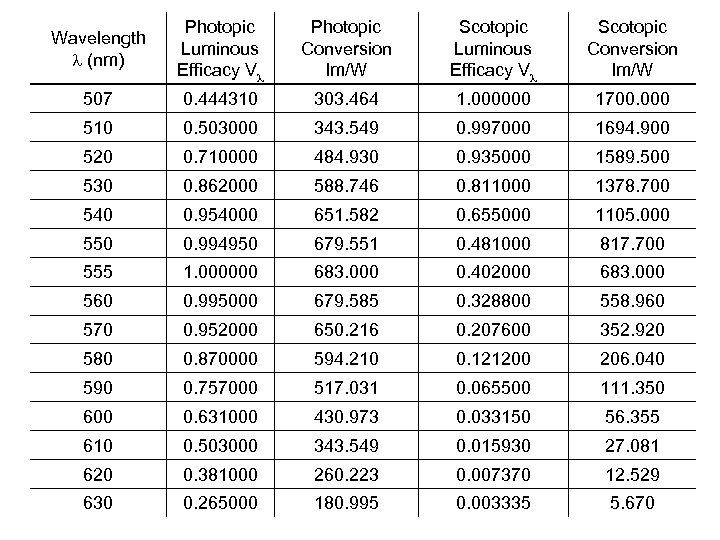 Wavelength l (nm) Photopic Luminous Efficacy Vl Photopic Conversion lm/W Scotopic Luminous Efficacy Vl Scotopic Conversion lm/W 507 0. 444310 303. 464 1. 000000 1700. 000 510 0. 503000 343. 549 0. 997000 1694. 900 520 0. 710000 484. 930 0. 935000 1589. 500 530 0. 862000 588. 746 0. 811000 1378. 700 540 0. 954000 651. 582 0. 655000 1105. 000 550 0. 994950 679. 551 0. 481000 817. 700 555 1. 000000 683. 000 0. 402000 683. 000 560 0. 995000 679. 585 0. 328800 558. 960 570 0. 952000 650. 216 0. 207600 352. 920 580 0. 870000 594. 210 0. 121200 206. 040 590 0. 757000 517. 031 0. 065500 111. 350 600 0. 631000 430. 973 0. 033150 56. 355 610 0. 503000 343. 549 0. 015930 27. 081 620 0. 381000 260. 223 0. 007370 12. 529 630 0. 265000 180. 995 0. 003335 5. 670
Wavelength l (nm) Photopic Luminous Efficacy Vl Photopic Conversion lm/W Scotopic Luminous Efficacy Vl Scotopic Conversion lm/W 507 0. 444310 303. 464 1. 000000 1700. 000 510 0. 503000 343. 549 0. 997000 1694. 900 520 0. 710000 484. 930 0. 935000 1589. 500 530 0. 862000 588. 746 0. 811000 1378. 700 540 0. 954000 651. 582 0. 655000 1105. 000 550 0. 994950 679. 551 0. 481000 817. 700 555 1. 000000 683. 000 0. 402000 683. 000 560 0. 995000 679. 585 0. 328800 558. 960 570 0. 952000 650. 216 0. 207600 352. 920 580 0. 870000 594. 210 0. 121200 206. 040 590 0. 757000 517. 031 0. 065500 111. 350 600 0. 631000 430. 973 0. 033150 56. 355 610 0. 503000 343. 549 0. 015930 27. 081 620 0. 381000 260. 223 0. 007370 12. 529 630 0. 265000 180. 995 0. 003335 5. 670
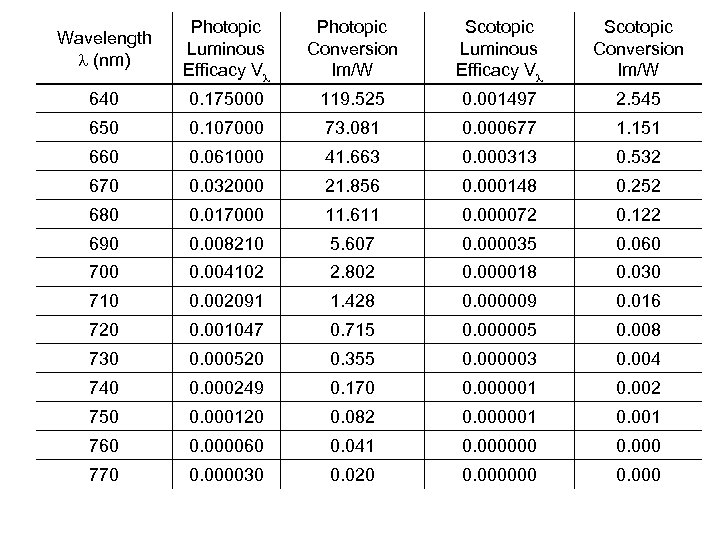 Wavelength l (nm) Photopic Luminous Efficacy Vl Photopic Conversion lm/W Scotopic Luminous Efficacy Vl Scotopic Conversion lm/W 640 0. 175000 119. 525 0. 001497 2. 545 650 0. 107000 73. 081 0. 000677 1. 151 660 0. 061000 41. 663 0. 000313 0. 532 670 0. 032000 21. 856 0. 000148 0. 252 680 0. 017000 11. 611 0. 000072 0. 122 690 0. 008210 5. 607 0. 000035 0. 060 700 0. 004102 2. 802 0. 000018 0. 030 710 0. 002091 1. 428 0. 000009 0. 016 720 0. 001047 0. 715 0. 000005 0. 008 730 0. 000520 0. 355 0. 000003 0. 004 740 0. 000249 0. 170 0. 000001 0. 002 750 0. 000120 0. 082 0. 000001 0. 001 760 0. 000060 0. 041 0. 000000 0. 000 770 0. 000030 0. 020 0. 000000 0. 000
Wavelength l (nm) Photopic Luminous Efficacy Vl Photopic Conversion lm/W Scotopic Luminous Efficacy Vl Scotopic Conversion lm/W 640 0. 175000 119. 525 0. 001497 2. 545 650 0. 107000 73. 081 0. 000677 1. 151 660 0. 061000 41. 663 0. 000313 0. 532 670 0. 032000 21. 856 0. 000148 0. 252 680 0. 017000 11. 611 0. 000072 0. 122 690 0. 008210 5. 607 0. 000035 0. 060 700 0. 004102 2. 802 0. 000018 0. 030 710 0. 002091 1. 428 0. 000009 0. 016 720 0. 001047 0. 715 0. 000005 0. 008 730 0. 000520 0. 355 0. 000003 0. 004 740 0. 000249 0. 170 0. 000001 0. 002 750 0. 000120 0. 082 0. 000001 0. 001 760 0. 000060 0. 041 0. 000000 0. 000 770 0. 000030 0. 020 0. 000000 0. 000
 Power Per Unit Solid Angle The power (flux) per unit solid angle (sometimes called pointance) is the nearest precise terminology to the common term intensity. It expresses the directionality of the radiated energy and is appropriate for the description of point sources. In the case of radiant power, it is expressed in watts per steradian. In photometry it is expressed in lumens per steradian = candela. The candela is the foundation unit for the measurement of visible light. It is one of the seven foundation SI units. It's formal definition is: The candela is the luminous intensity, in a given direction. of a source that emits monochromatic radiation of frequency 540 x 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian. The candela is abbreviated cd and its Standard symbol is Iv. The candela is then used to define the lumen and other quantities used in the measurement of visible light.
Power Per Unit Solid Angle The power (flux) per unit solid angle (sometimes called pointance) is the nearest precise terminology to the common term intensity. It expresses the directionality of the radiated energy and is appropriate for the description of point sources. In the case of radiant power, it is expressed in watts per steradian. In photometry it is expressed in lumens per steradian = candela. The candela is the foundation unit for the measurement of visible light. It is one of the seven foundation SI units. It's formal definition is: The candela is the luminous intensity, in a given direction. of a source that emits monochromatic radiation of frequency 540 x 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian. The candela is abbreviated cd and its Standard symbol is Iv. The candela is then used to define the lumen and other quantities used in the measurement of visible light.
 Power Per Unit Area Per Unit Solid Angle The power per unit area per unit solid angle is sometimes called sterance. In the radiant case it is measured in watts/m 2 steradian and is also called radiance. In the luminous case it is measured in lumens/m 2 steradian which is equivalent to candela/m 2 = nit. This quantity is also called luminance. Power Per Unit Area of Surface The power per unit area on an illuminated surface, sometimes called areance, is distinguished from the similar quantity for the source. In radiometry the surface areance may be called irradiance and luminous areance may be called illuminance. This is the quantity of practical importance in judging whether an area is lighted well enough for reading or other activities. The illuminance is measured in lux. The lux is defined as a lumen per square meter and is a unit of illuminance. An equivalent term is luminous flux density. Illuminance Ev = Luminous intensity Iv /radius 2
Power Per Unit Area Per Unit Solid Angle The power per unit area per unit solid angle is sometimes called sterance. In the radiant case it is measured in watts/m 2 steradian and is also called radiance. In the luminous case it is measured in lumens/m 2 steradian which is equivalent to candela/m 2 = nit. This quantity is also called luminance. Power Per Unit Area of Surface The power per unit area on an illuminated surface, sometimes called areance, is distinguished from the similar quantity for the source. In radiometry the surface areance may be called irradiance and luminous areance may be called illuminance. This is the quantity of practical importance in judging whether an area is lighted well enough for reading or other activities. The illuminance is measured in lux. The lux is defined as a lumen per square meter and is a unit of illuminance. An equivalent term is luminous flux density. Illuminance Ev = Luminous intensity Iv /radius 2
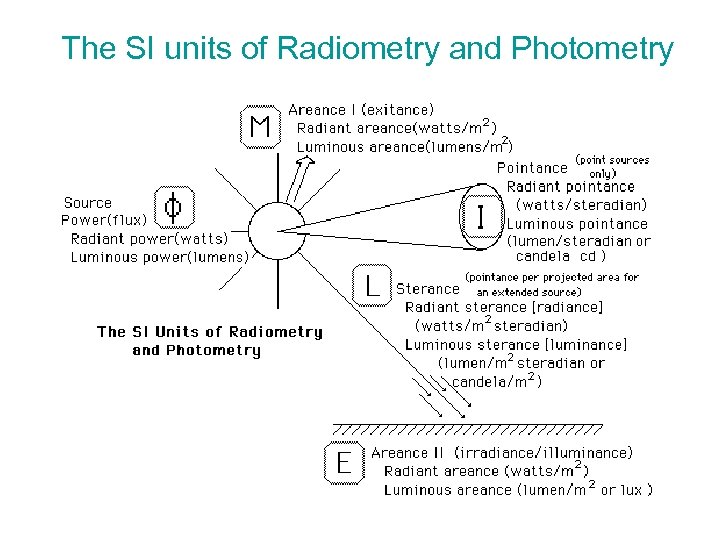 The SI units of Radiometry and Photometry
The SI units of Radiometry and Photometry
 Radiometry Summary Quantityr Abbr. Notes SI radiometry units Radiant energy J energy Radiant flux W radiant energy per unit time, also called radiant power Radiant intensity W·sr− 1 power per unit solid angle Radiance W·sr− 1·m− 2 power per unit solid angle per unit projected source area. Sometimes confusingly called "intensity". Irradiance W·m− 2 power incident on a surface. Radiant emittance / Radiant exitance W·m− 2 Sometimes confusingly called "intensity". power emitted from a surface. Spectral radiance W·sr− 1·m− 3 Sometimes confusingly called "intensity". commonly measured in W·sr− 1·m− 2·nm− 1 or W·sr− 1·m− 2· Hz− 1 Spectral irradiance W·m− 3 or W·m− 2·Hz− 1 commonly measured in W·m− 2·nm− 1
Radiometry Summary Quantityr Abbr. Notes SI radiometry units Radiant energy J energy Radiant flux W radiant energy per unit time, also called radiant power Radiant intensity W·sr− 1 power per unit solid angle Radiance W·sr− 1·m− 2 power per unit solid angle per unit projected source area. Sometimes confusingly called "intensity". Irradiance W·m− 2 power incident on a surface. Radiant emittance / Radiant exitance W·m− 2 Sometimes confusingly called "intensity". power emitted from a surface. Spectral radiance W·sr− 1·m− 3 Sometimes confusingly called "intensity". commonly measured in W·sr− 1·m− 2·nm− 1 or W·sr− 1·m− 2· Hz− 1 Spectral irradiance W·m− 3 or W·m− 2·Hz− 1 commonly measured in W·m− 2·nm− 1
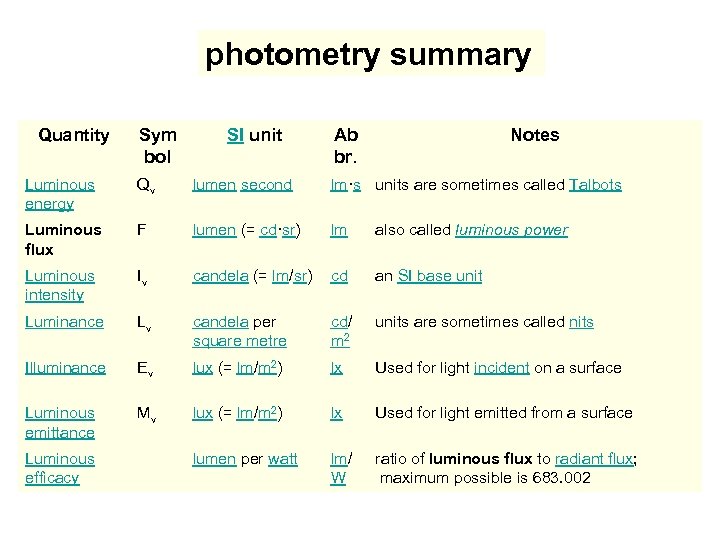 photometry summary Quantity Sym bol SI unit Ab br. Notes Luminous energy Qv lumen second lm·s units are sometimes called Talbots Luminous flux F lumen (= cd·sr) lm also called luminous power Luminous intensity Iv candela (= lm/sr) cd an SI base unit Luminance Lv candela per square metre cd/ m 2 units are sometimes called nits Illuminance Ev lux (= lm/m 2) lx Used for light incident on a surface Luminous emittance Mv lux (= lm/m 2) lx Used for light emitted from a surface Luminous efficacy lumen per watt lm/ W ratio of luminous flux to radiant flux; maximum possible is 683. 002
photometry summary Quantity Sym bol SI unit Ab br. Notes Luminous energy Qv lumen second lm·s units are sometimes called Talbots Luminous flux F lumen (= cd·sr) lm also called luminous power Luminous intensity Iv candela (= lm/sr) cd an SI base unit Luminance Lv candela per square metre cd/ m 2 units are sometimes called nits Illuminance Ev lux (= lm/m 2) lx Used for light incident on a surface Luminous emittance Mv lux (= lm/m 2) lx Used for light emitted from a surface Luminous efficacy lumen per watt lm/ W ratio of luminous flux to radiant flux; maximum possible is 683. 002
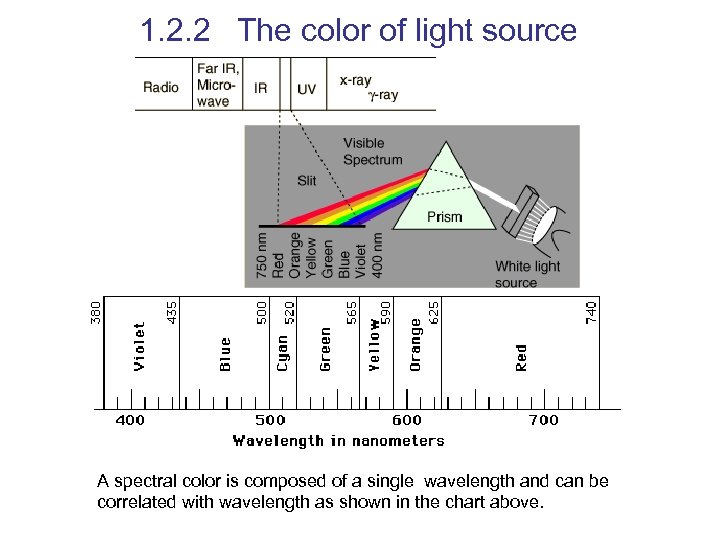 1. 2. 2 The color of light source A spectral color is composed of a single wavelength and can be correlated with wavelength as shown in the chart above.
1. 2. 2 The color of light source A spectral color is composed of a single wavelength and can be correlated with wavelength as shown in the chart above.
 The characteristics of color: hue, saturation, and brightness It is common practice to define pure colors in terms of the wavelengths of light as shown. This works well for spectral colors but it is found that many different combinations of light wavelengths can produce the same perception of color. The inherently distinguishable characteristics of color are hue, saturation, and brightness. Color measurement systems characterize colors in various parameters which relate to hue, saturation, and brightness. They include the subjective Munsell and Ostwald systems and the quantitative CIE color system.
The characteristics of color: hue, saturation, and brightness It is common practice to define pure colors in terms of the wavelengths of light as shown. This works well for spectral colors but it is found that many different combinations of light wavelengths can produce the same perception of color. The inherently distinguishable characteristics of color are hue, saturation, and brightness. Color measurement systems characterize colors in various parameters which relate to hue, saturation, and brightness. They include the subjective Munsell and Ostwald systems and the quantitative CIE color system.
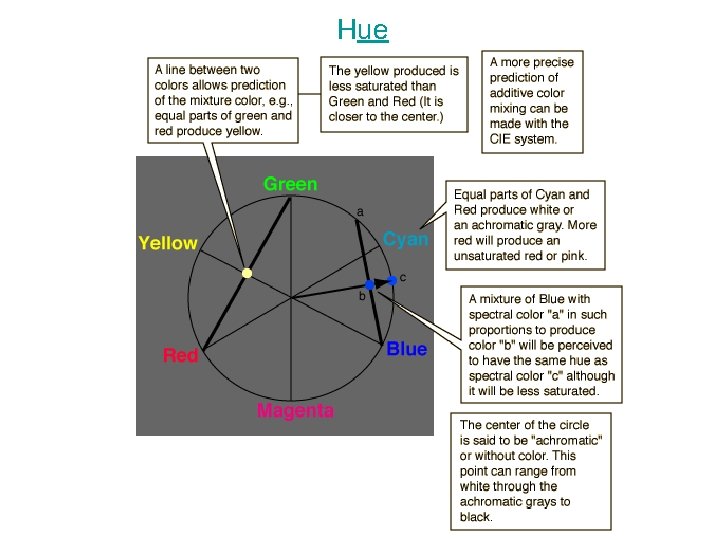
 Hue The Newton Color Circle The terms "red" and "blue“ primarily describe hue – hue is related to wavelength for spectral colors. It is convenient to arrange the saturated hues around a Newton Color Circle. Starting from red and proceeding clockwise around the circle below to blue proceeds from long to shorter wavelengths. However it shows that not all hues can be represented by spectral colors since there is no single wavelength of light which has the magenta hue - it may be produced by an equal mixture of red and blue. Newton's color circle is a convenient way to summarize the additive mixing properties of colors. R, G, B are thought of as the additive primary colors, and their complementary colors are placed across from them on the circle. The colors then fall on the circle in the order of the wavelengths of the corresponding spectral colors. Magenta is not a spectra color.
Hue The Newton Color Circle The terms "red" and "blue“ primarily describe hue – hue is related to wavelength for spectral colors. It is convenient to arrange the saturated hues around a Newton Color Circle. Starting from red and proceeding clockwise around the circle below to blue proceeds from long to shorter wavelengths. However it shows that not all hues can be represented by spectral colors since there is no single wavelength of light which has the magenta hue - it may be produced by an equal mixture of red and blue. Newton's color circle is a convenient way to summarize the additive mixing properties of colors. R, G, B are thought of as the additive primary colors, and their complementary colors are placed across from them on the circle. The colors then fall on the circle in the order of the wavelengths of the corresponding spectral colors. Magenta is not a spectra color.
 Hue
Hue
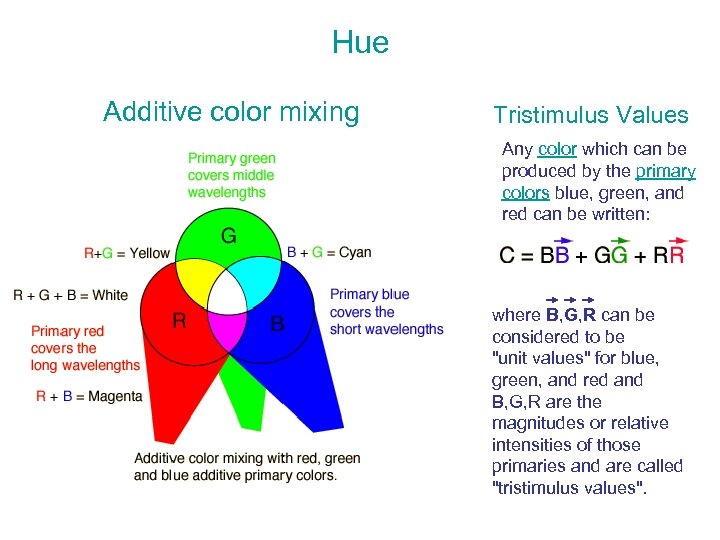 Hue Additive color mixing Tristimulus Values Any color which can be produced by the primary colors blue, green, and red can be written: where B, G, R can be considered to be "unit values" for blue, green, and red and B, G, R are the magnitudes or relative intensities of those primaries and are called "tristimulus values".
Hue Additive color mixing Tristimulus Values Any color which can be produced by the primary colors blue, green, and red can be written: where B, G, R can be considered to be "unit values" for blue, green, and red and B, G, R are the magnitudes or relative intensities of those primaries and are called "tristimulus values".
 saturation Pink may be thought of as having the same hue as red but being less saturated. A fully saturated color is one with no mixture of white. A spectral color consisting of only one wavelength is fully saturated, but one can have a fully saturated magenta which is not a spectral color. Note that the blue of the sky is more saturated when you look further from the sun. The almost white scattering near the sun can be attributed to Mie scattering, which is not very wavelength dependent. The mixture of white light with the blue gives a less saturated blue.
saturation Pink may be thought of as having the same hue as red but being less saturated. A fully saturated color is one with no mixture of white. A spectral color consisting of only one wavelength is fully saturated, but one can have a fully saturated magenta which is not a spectral color. Note that the blue of the sky is more saturated when you look further from the sun. The almost white scattering near the sun can be attributed to Mie scattering, which is not very wavelength dependent. The mixture of white light with the blue gives a less saturated blue.
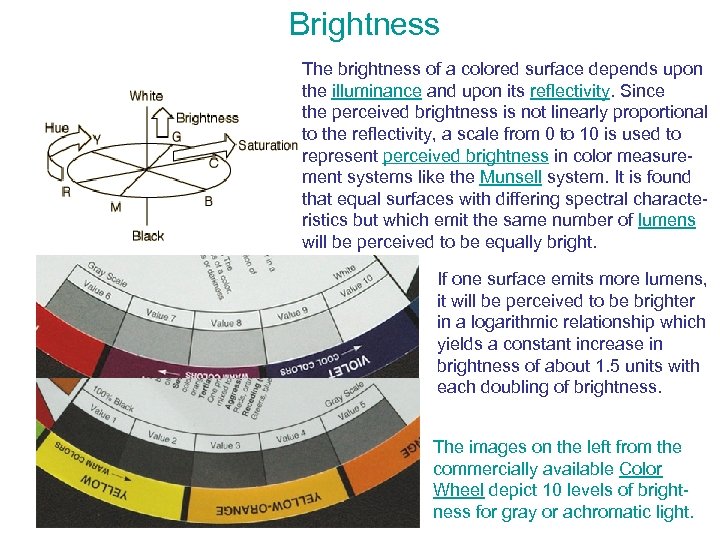 Brightness The brightness of a colored surface depends upon the illuminance and upon its reflectivity. Since the perceived brightness is not linearly proportional to the reflectivity, a scale from 0 to 10 is used to represent perceived brightness in color measurement systems like the Munsell system. It is found that equal surfaces with differing spectral characteristics but which emit the same number of lumens will be perceived to be equally bright. If one surface emits more lumens, it will be perceived to be brighter in a logarithmic relationship which yields a constant increase in brightness of about 1. 5 units with each doubling of brightness. The images on the left from the commercially available Color Wheel depict 10 levels of brightness for gray or achromatic light.
Brightness The brightness of a colored surface depends upon the illuminance and upon its reflectivity. Since the perceived brightness is not linearly proportional to the reflectivity, a scale from 0 to 10 is used to represent perceived brightness in color measurement systems like the Munsell system. It is found that equal surfaces with differing spectral characteristics but which emit the same number of lumens will be perceived to be equally bright. If one surface emits more lumens, it will be perceived to be brighter in a logarithmic relationship which yields a constant increase in brightness of about 1. 5 units with each doubling of brightness. The images on the left from the commercially available Color Wheel depict 10 levels of brightness for gray or achromatic light.
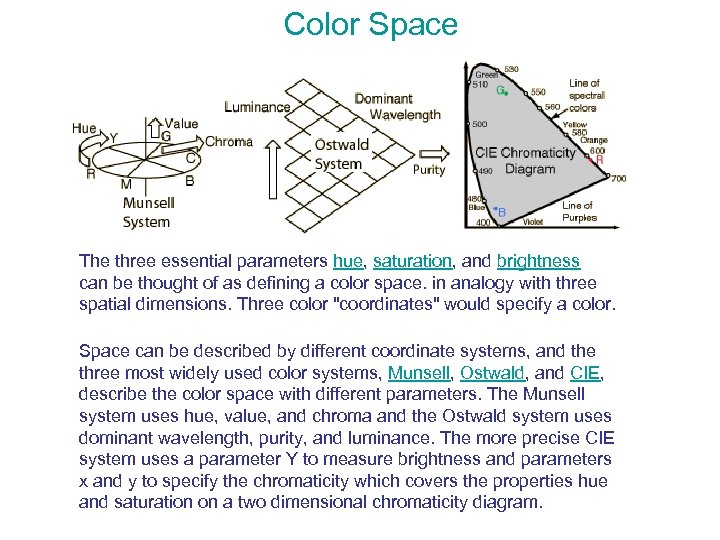 Color Space The three essential parameters hue, saturation, and brightness can be thought of as defining a color space. in analogy with three spatial dimensions. Three color "coordinates" would specify a color. Space can be described by different coordinate systems, and the three most widely used color systems, Munsell, Ostwald, and CIE, describe the color space with different parameters. The Munsell system uses hue, value, and chroma and the Ostwald system uses dominant wavelength, purity, and luminance. The more precise CIE system uses a parameter Y to measure brightness and parameters x and y to specify the chromaticity which covers the properties hue and saturation on a two dimensional chromaticity diagram.
Color Space The three essential parameters hue, saturation, and brightness can be thought of as defining a color space. in analogy with three spatial dimensions. Three color "coordinates" would specify a color. Space can be described by different coordinate systems, and the three most widely used color systems, Munsell, Ostwald, and CIE, describe the color space with different parameters. The Munsell system uses hue, value, and chroma and the Ostwald system uses dominant wavelength, purity, and luminance. The more precise CIE system uses a parameter Y to measure brightness and parameters x and y to specify the chromaticity which covers the properties hue and saturation on a two dimensional chromaticity diagram.
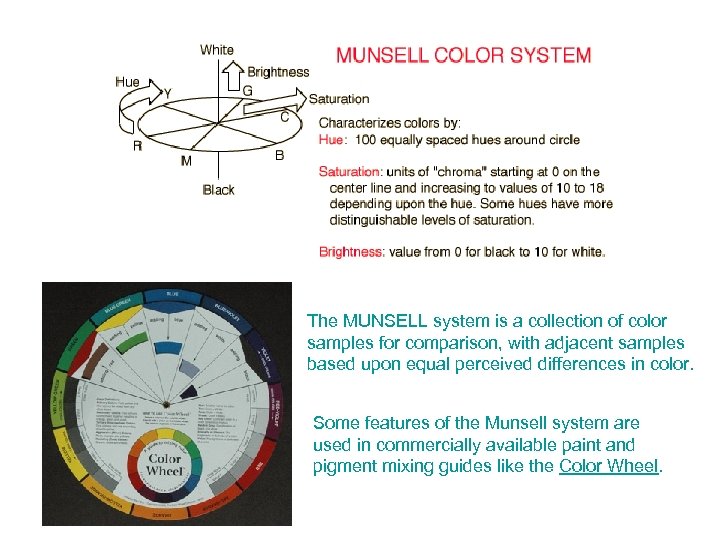 The MUNSELL system is a collection of color samples for comparison, with adjacent samples based upon equal perceived differences in color. Some features of the Munsell system are used in commercially available paint and pigment mixing guides like the Color Wheel.
The MUNSELL system is a collection of color samples for comparison, with adjacent samples based upon equal perceived differences in color. Some features of the Munsell system are used in commercially available paint and pigment mixing guides like the Color Wheel.
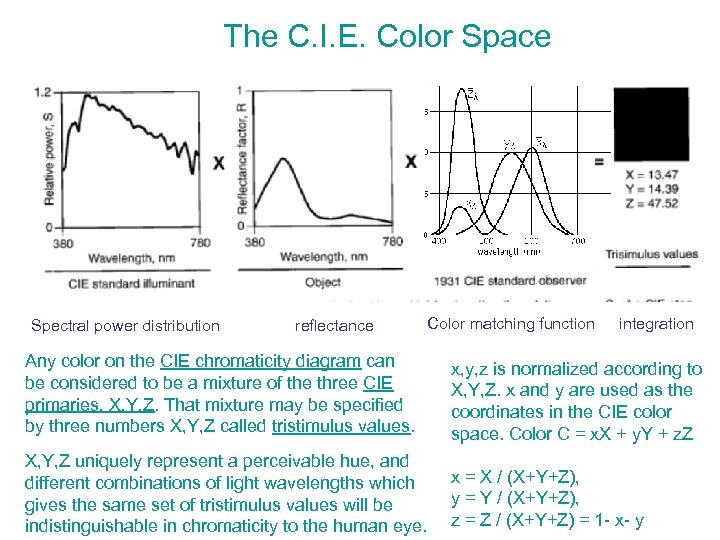 The C. I. E. Color Space Spectral power distribution reflectance Color matching function integration Any color on the CIE chromaticity diagram can be considered to be a mixture of the three CIE primaries, X, Y, Z. That mixture may be specified by three numbers X, Y, Z called tristimulus values. x, y, z is normalized according to X, Y, Z. x and y are used as the coordinates in the CIE color space. Color C = x. X + y. Y + z. Z X, Y, Z uniquely represent a perceivable hue, and different combinations of light wavelengths which gives the same set of tristimulus values will be indistinguishable in chromaticity to the human eye. x = X / (X+Y+Z), y = Y / (X+Y+Z), z = Z / (X+Y+Z) = 1 - x- y
The C. I. E. Color Space Spectral power distribution reflectance Color matching function integration Any color on the CIE chromaticity diagram can be considered to be a mixture of the three CIE primaries, X, Y, Z. That mixture may be specified by three numbers X, Y, Z called tristimulus values. x, y, z is normalized according to X, Y, Z. x and y are used as the coordinates in the CIE color space. Color C = x. X + y. Y + z. Z X, Y, Z uniquely represent a perceivable hue, and different combinations of light wavelengths which gives the same set of tristimulus values will be indistinguishable in chromaticity to the human eye. x = X / (X+Y+Z), y = Y / (X+Y+Z), z = Z / (X+Y+Z) = 1 - x- y
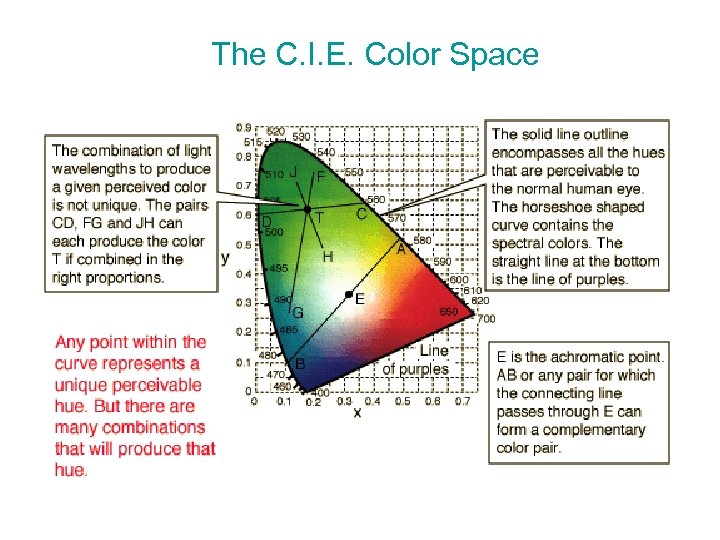 The C. I. E. Color Space
The C. I. E. Color Space
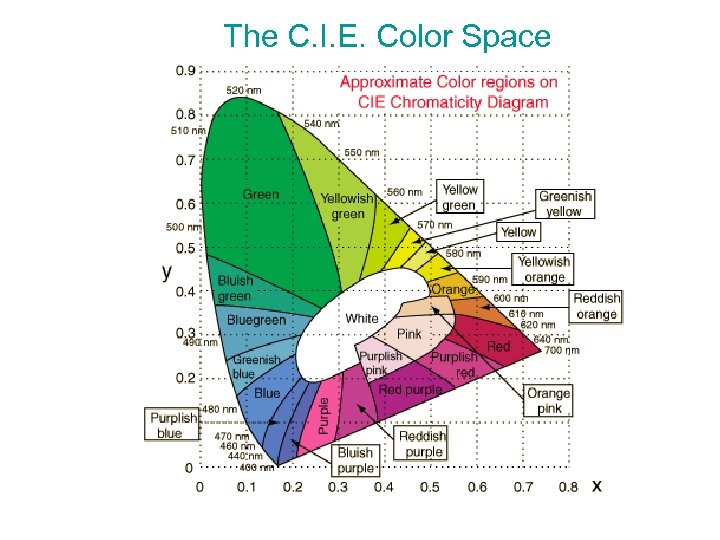 The C. I. E. Color Space
The C. I. E. Color Space
 Color Temperature An incandescent light is very close to being a black-body radiator. Of all colors based on the black body blue is the "hotter" color, while red is actually the "cooler" color. This is the opposite of the associations both colors have taken on, with "red" as "hot", and "blue" as "cold". A proof of this is that while incandescent bulbs glow a reddish to yellowish color throughout their lifetimes, when one blows out, the flash of light is noticeably bluish. The filament is hotter when it burns out. 5000 K and 6500 K are also called respectively D 50 (US standard) and D 65 (Europe standard) in all professions working with light (photographers, publishers, etc). It is a temperature similar to the black body temperature but not strictly identical.
Color Temperature An incandescent light is very close to being a black-body radiator. Of all colors based on the black body blue is the "hotter" color, while red is actually the "cooler" color. This is the opposite of the associations both colors have taken on, with "red" as "hot", and "blue" as "cold". A proof of this is that while incandescent bulbs glow a reddish to yellowish color throughout their lifetimes, when one blows out, the flash of light is noticeably bluish. The filament is hotter when it burns out. 5000 K and 6500 K are also called respectively D 50 (US standard) and D 65 (Europe standard) in all professions working with light (photographers, publishers, etc). It is a temperature similar to the black body temperature but not strictly identical.
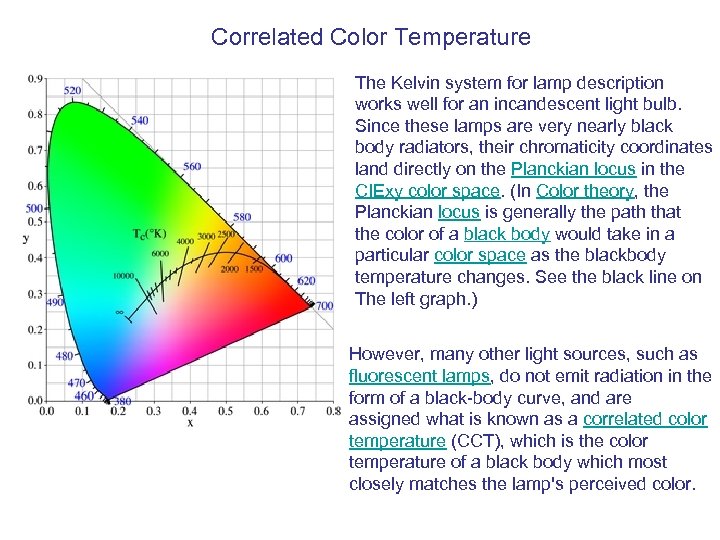 Correlated Color Temperature The Kelvin system for lamp description works well for an incandescent light bulb. Since these lamps are very nearly black body radiators, their chromaticity coordinates land directly on the Planckian locus in the CIExy color space. (In Color theory, the Planckian locus is generally the path that the color of a black body would take in a particular color space as the blackbody temperature changes. See the black line on The left graph. ) However, many other light sources, such as fluorescent lamps, do not emit radiation in the form of a black-body curve, and are assigned what is known as a correlated color temperature (CCT), which is the color temperature of a black body which most closely matches the lamp's perceived color.
Correlated Color Temperature The Kelvin system for lamp description works well for an incandescent light bulb. Since these lamps are very nearly black body radiators, their chromaticity coordinates land directly on the Planckian locus in the CIExy color space. (In Color theory, the Planckian locus is generally the path that the color of a black body would take in a particular color space as the blackbody temperature changes. See the black line on The left graph. ) However, many other light sources, such as fluorescent lamps, do not emit radiation in the form of a black-body curve, and are assigned what is known as a correlated color temperature (CCT), which is the color temperature of a black body which most closely matches the lamp's perceived color.
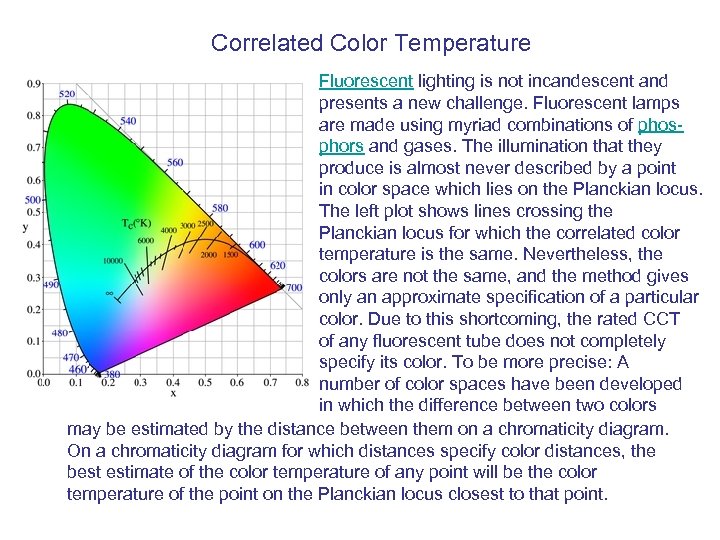 Correlated Color Temperature Fluorescent lighting is not incandescent and presents a new challenge. Fluorescent lamps are made using myriad combinations of phosphors and gases. The illumination that they produce is almost never described by a point in color space which lies on the Planckian locus. The left plot shows lines crossing the Planckian locus for which the correlated color temperature is the same. Nevertheless, the colors are not the same, and the method gives only an approximate specification of a particular color. Due to this shortcoming, the rated CCT of any fluorescent tube does not completely specify its color. To be more precise: A number of color spaces have been developed in which the difference between two colors may be estimated by the distance between them on a chromaticity diagram. On a chromaticity diagram for which distances specify color distances, the best estimate of the color temperature of any point will be the color temperature of the point on the Planckian locus closest to that point.
Correlated Color Temperature Fluorescent lighting is not incandescent and presents a new challenge. Fluorescent lamps are made using myriad combinations of phosphors and gases. The illumination that they produce is almost never described by a point in color space which lies on the Planckian locus. The left plot shows lines crossing the Planckian locus for which the correlated color temperature is the same. Nevertheless, the colors are not the same, and the method gives only an approximate specification of a particular color. Due to this shortcoming, the rated CCT of any fluorescent tube does not completely specify its color. To be more precise: A number of color spaces have been developed in which the difference between two colors may be estimated by the distance between them on a chromaticity diagram. On a chromaticity diagram for which distances specify color distances, the best estimate of the color temperature of any point will be the color temperature of the point on the Planckian locus closest to that point.


