Fundamentals of Data Analysis Four Types of

Fundamentals of Data Analysis

Four Types of Data • Alphabetical / Categorical / Nominal data: – Information falls only in certain categories, not in-between categories – No inferences possible between groups except that one group may contain more / less observations than the other – Only reporting frequencies, percentages and mode makes sense (descriptive statistics) – Chi Square measure of Association (inferential Statistics) – Examples: gender, age groups, income groups, etc.

Four Types of data • Rank order data: – Ranked according to some logic, e. g. preference, etc. – Again an in-between rank does not make sense. – Difference between say rank 1 and 2 need not necessarily be of the same magnitude as the difference between rank 3 and 4. – Only reporting frequencies, percentages and mode makes sense (descriptive statistics); Spearman Rho coefficient of correlation (Inferential statistics) – Examples: brand preferences, class rank on test, etc.

Four Types of data • Interval Level – Numerical data in which the numbers denote the amount of presence / absence of a trait. – zero point does not necessarily mean complete absence of the trait – In-between numbers make sense – Magnitude of difference between numbers on the scale is constant. – All descriptive and inferential statistics possible – Examples: attitude, satisfaction, temperature, etc.

Four Types of data • Ratio level data – Interval level data with a meaningful zero point meaning complete absence of the trait – Magnitude of the difference between numbers of the scale is constant AND the zero point denotes complete absence of the trait being measured. – All descriptive and inferential statistics possible – Examples: sales, profits, weight, height, etc.

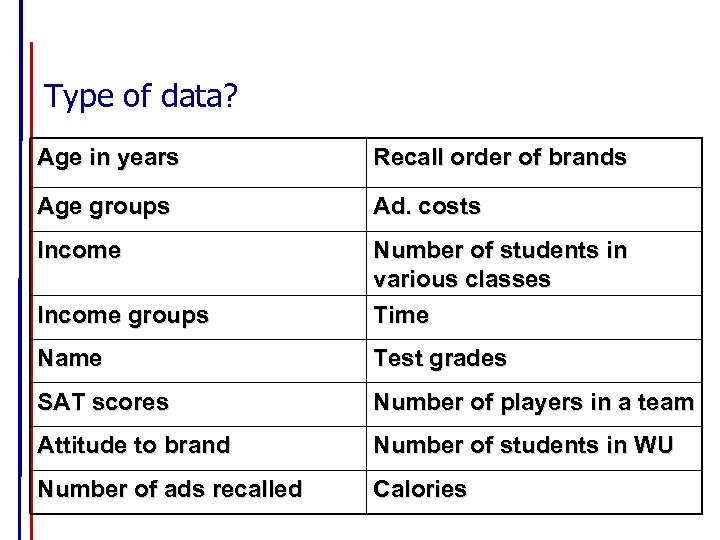Type of data? Age in years Recall order of brands Age groups Ad. costs Income groups Number of students in various classes Time Name Test grades SAT scores Number of players in a team Attitude to brand Number of students in WU Number of ads recalled Calories

Preparing the Data for Analysis • Data editing – the process of identifying omissions, ambiguities and errors in the responses • Coding – process of assigning numerical values to responses according to a pre-defined system • Statistically adjusting the data – the process of modifying the data to enhance its quality for analysis – Weighting, transformations, variable re-specification

Preparing the Data for Analysis Problems Identified With Data Editing • Omissions – some unanswered questions • Ambiguity – illegible response, choosing two boxes when only one has to be chosen • Inconsistencies – logically inconsistent response • Lack of Cooperation – checking the same response regardless of the question • Ineligible Respondent – ignoring a filter question

Preparing the Data for Analysis • Solutions to such problems – – – Contact the respondent again and make corrections Throw out the whole questionnaire as unusable Disregard questions with missing values in the analysis Code illegible or missing responses as ‘don’t know’ Compute missing values on the basis of means

Preparing the Data for Analysis Coding • closed-ended questions – Relatively simple and straightforward • open-ended questions – Define all possible responses and categorize each response and then assign a numerical code – If judgment calls are needed then have several coders do the same task and check inter-coder reliability

Statistical adjustment of data • Weighting – – process of enhancing / reducing the importance of certain data by assigning a number – Usually done to increase the representativeness of the sample or achieve study objectives – E. g. a sports drink survey would weigh younger respondents higher than older respondents • Scale transformations – Manipulation of scales to make them comparable with other scales e. g. converting lbs to kgs. etc. – Z-scores (standardized scales)

Preparing the Data for Analysis • Variable Re-specification – Existing data modified to create new variables – Large number of variables collapsed into fewer variables – Creates variables that are consistent with research questions • Determine if the variable is categorical, rankorder, interval level or ratio level.

Categorical Data Analysis - Objectives • Describing the sample distribution for the variable (e. g. gender) • Frequencies, percentages, quartiles, percentiles, graphs (bar, line, histogram, pie) • What are the typical characteristics of the sample? • Mode • Does the categorical variable bear any relationship with a distribution of another categorical variable (e. g. gender w. r. t. buy the product or not) • Cross tabs and chi-square as a measure of association

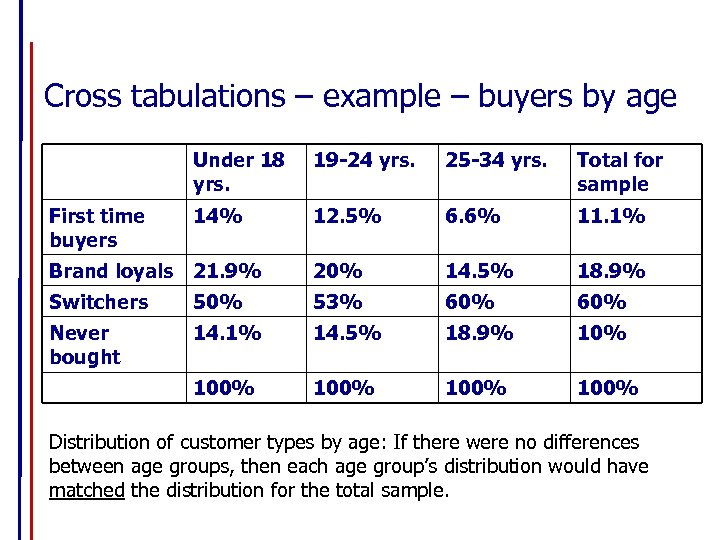Cross tabulations – example – buyers by age Under 18 yrs. 19 -24 yrs. 25 -34 yrs. Total for sample First time buyers 14% 12. 5% 6. 6% 11. 1% Brand loyals 21. 9% 20% 14. 5% 18. 9% Switchers 50% 53% 60% Never bought 14. 1% 14. 5% 18. 9% 100% 100% Distribution of customer types by age: If there were no differences between age groups, then each age group’s distribution would have matched the distribution for the total sample.

Crosstabs - conclusions • The 25 -34 yrs. Group is least likely to be first time buyers than the sample average • The under 18 year group is more likely to be a brand loyal than the sample average

Rank order data analysis - Objectives • What are respondent preferences amongst several competing alternatives? (e. g. rank your preferences amongst ten different brands of cars) – Frequencies, Percentages, Graphs • What is the typical preference pattern in the sample (e. g. which car does the sample prefer the most and which one the least? ) – Mode

Rank order data analysis - Objectives • Are two sets of respondent preferences correlated? (e. g. wrist watches brand preferences with car brand preferences) – Spearman’s rank correlation coefficient

Interval level / Ratio level data analysis - Objectives • What is the average response in the sample (e. g. what is the mean attitude to the brand? ) – Mean / Median • What is the average variability of the response in the sample (e. g. On an average, how dispersed are the sample’s attitudes to the brand from the mean? ) – Standard deviation

Interval level / Ratio level data analysis - Objectives • Do two or more subgroups in the sample differ from each other on the response / differ from a previously known / hypothesized value • E. g. do males like the brand significantly more than the females? (t tests, z tests) • E. g. Does attitude to WU vary by student status (freshman, sophomore, junior, senior) – ANOVA

Interval level / Ratio level data analysis - Objectives • Are sample responses on two variables correlated? (e. g. are sales related to the advertising expenditure? ) – Pearson correlation • Can we determine the value of the sample’s response on a variable, if we know the value on another variable? (e. g. If we need to achieve 1 million dollars in sales next year, how much should we spend on advertising? ) – Regression analysis