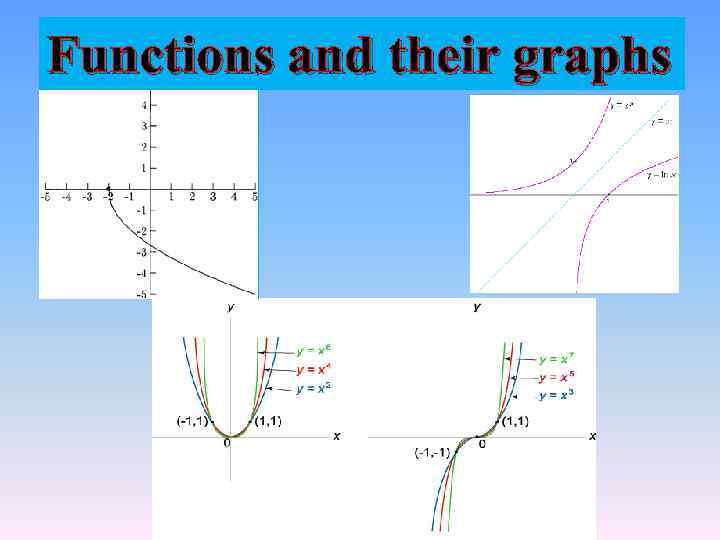
Functions and their graphs Quadratic function Field

Functions and their graphs

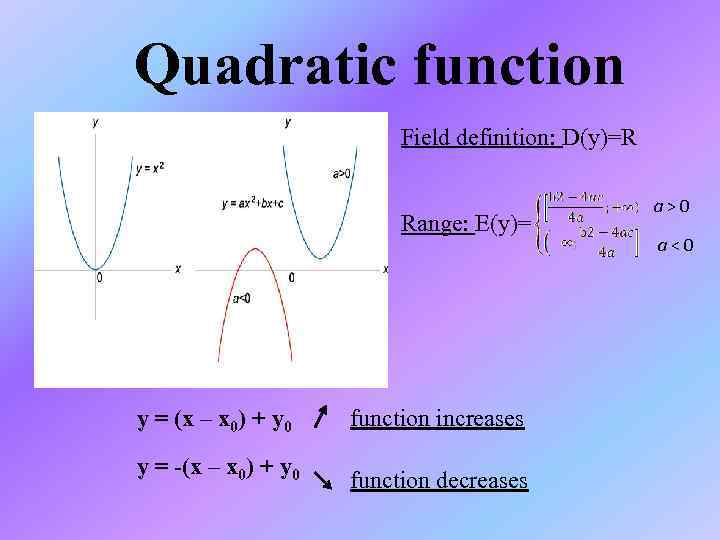Quadratic function Field definition: D(y)=R Range: E(y)= y = (x – x 0) + y 0 function increases y = -(x – x 0) + y 0 function decreases a > 0 a < 0

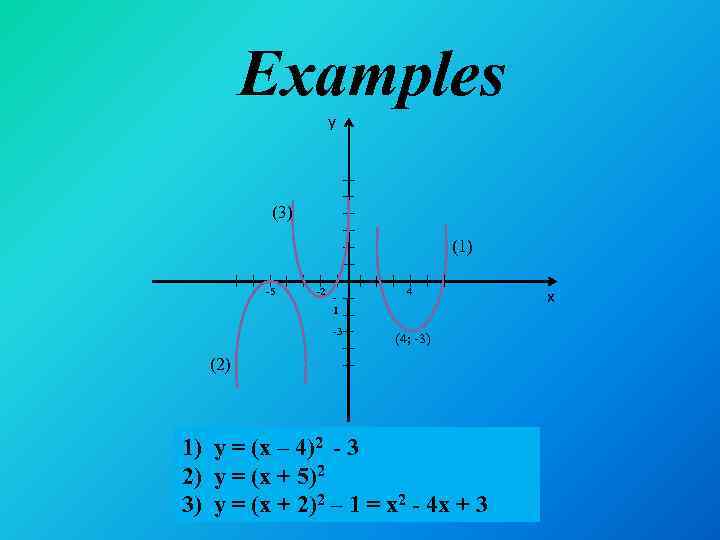Examples y (3) (1) -5 -2 1 -3 4 (4; -3) (2) 1) y = (x – 4)2 - 3 2) y = (x + 5)2 3) y = (x + 2)2 – 1 = x 2 - 4 x + 3 x

Exponential functions look somewhat similar to functions you have seen before, in that they involve exponents, but there is a big difference, in that the variable is now the power, rather than the base. Previously, you have dealt with such functions as f(x) = x 2, where the variable x was the base and the number 2 was the power. In the case of exponentials, however, you will be dealing with functions such as g(x) = 2 x, where the base is the fixed number, and the power is the variable.

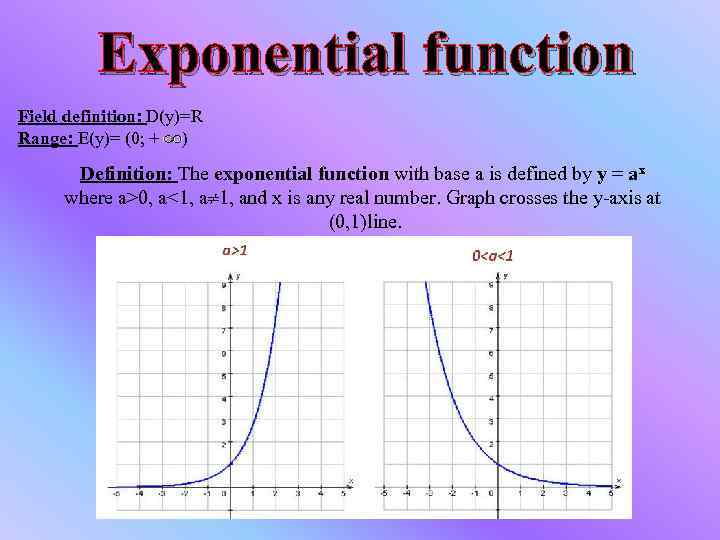Exponential function Field definition: D(y)=R Range: E(y)= (0; + ) Definition: The exponential function with base a is defined by y = ax where a>0, a<1, and x is any real number. Graph crosses the y-axis at (0, 1)line.

Examples y y = 5 x 5 1 -1 1 x

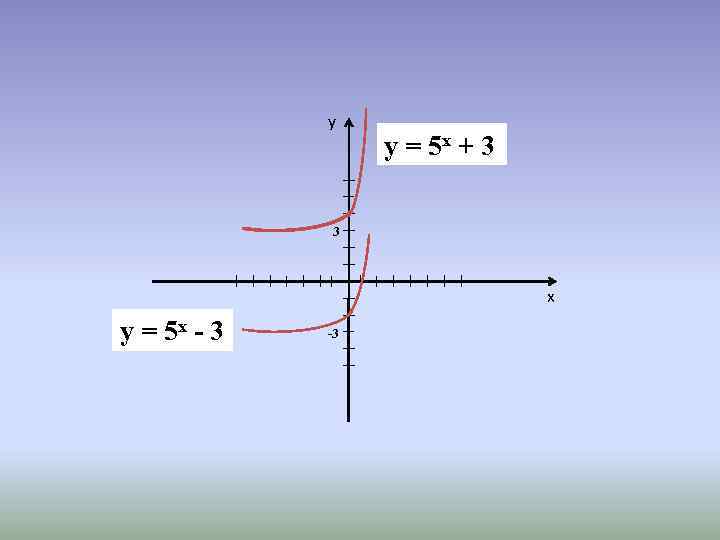y y = 5 x + 3 3 x y = 5 x - 3 -3

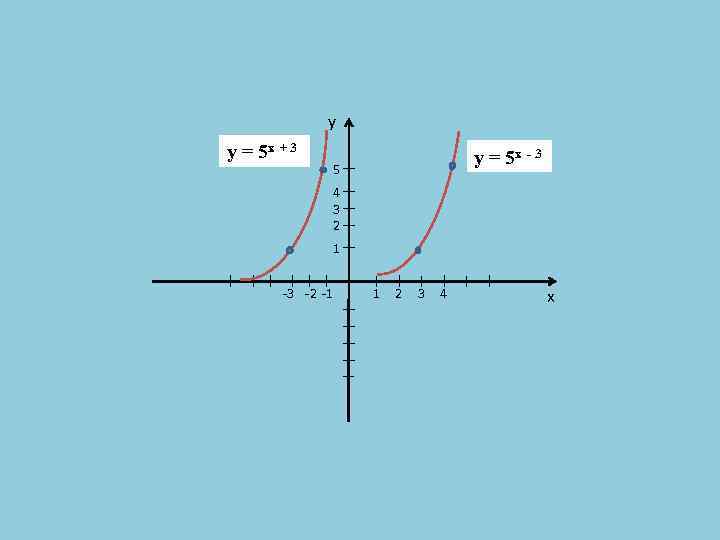y y = 5 x + 3 y = 5 x - 3 5 4 3 2 1 -3 -2 -1 1 2 3 4 x

y 8 7 6 5 4 3 2 1 -3 -2 -1 1 -1 -2 -3 2 3 4 x

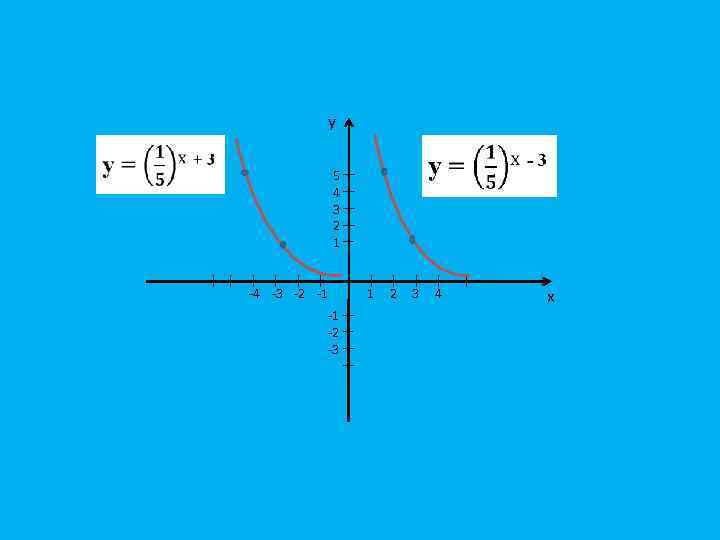y 5 4 3 2 1 -4 -3 -2 -1 -1 -2 -3 1 2 3 4 x

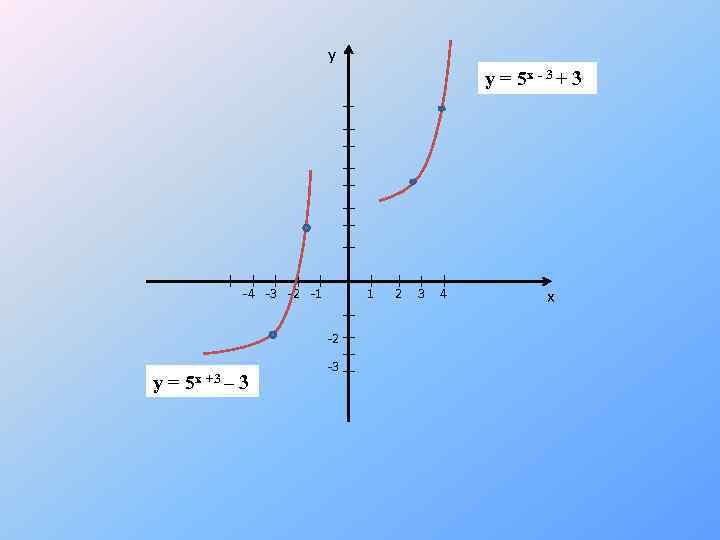y y = 5 x - 3 + 3 -4 -3 -2 -1 1 -2 y = 5 x +3 – 3 -3 2 3 4 x