Functional Programming Putting the fun in programming At

Functional Programming Putting the fun in programming At least I think so Kris. Aerts@kuleuven. be

Me, Myself & Functional Programming • • • 1991: Prolog 1992: sociology in LLN 1993: Haskell 1994: paper of Hudak 1999: paper Games provide fun(ctional programming tasks) in Functional and declarative programming in education, FDPE’ 99 • 2001: finished my Ph. D and started at KHLim Diepenbeek • Teaching ICT in master in industrial sciences (ing. ) o Capable in Java, not so much in. NET o Bit of functional programming in master 2/72

Hudak’s Paper • Experiment in 1994 3/72

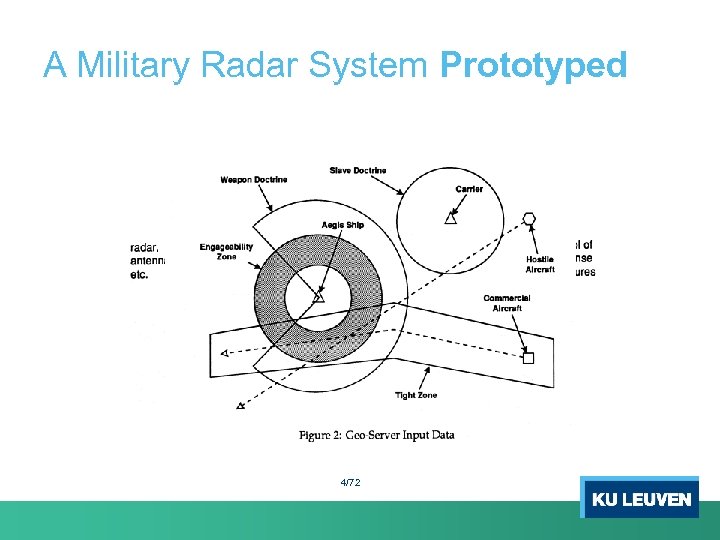A Military Radar System Prototyped 4/72

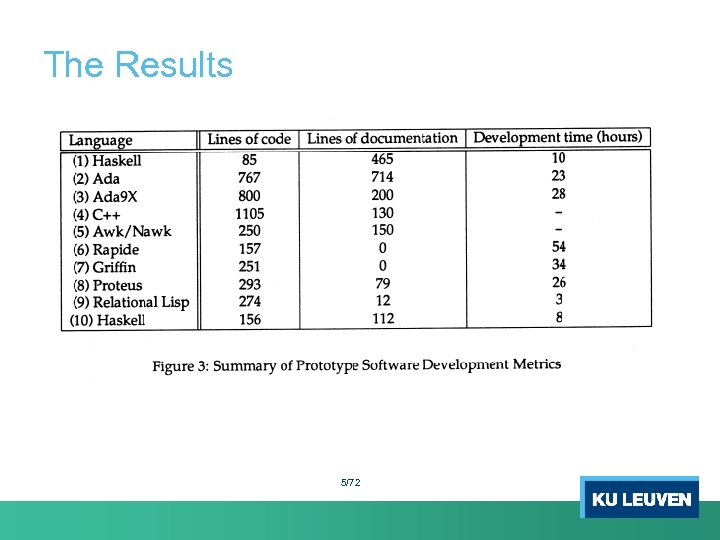The Results 5/72

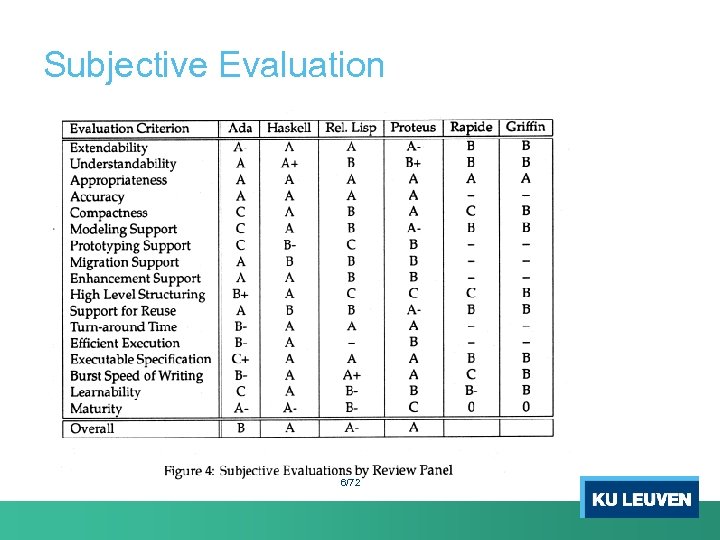Subjective Evaluation 6/72

Research in Functional Programming • • • Dia van Tom’s inaugurale Lisp: 1958 Haskell: Erlang Common Lisp: 1 e ANSI gestandaardiseerde taal met OO + FP 7/72

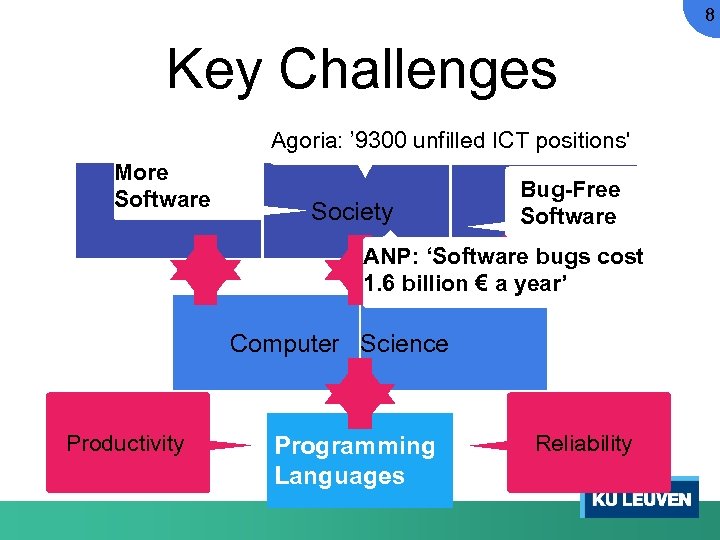8 Key Challenges Agoria: ’ 9300 unfilled ICT positions' More Software Society Bug-Free Software ANP: ‘Software bugs cost 1. 6 billion € a year’ Computer Science Productivity Programming Languages Reliability

9 Meeting the Challenges Incremental Research Mainstream languages Fundamental Research A different approach to languages

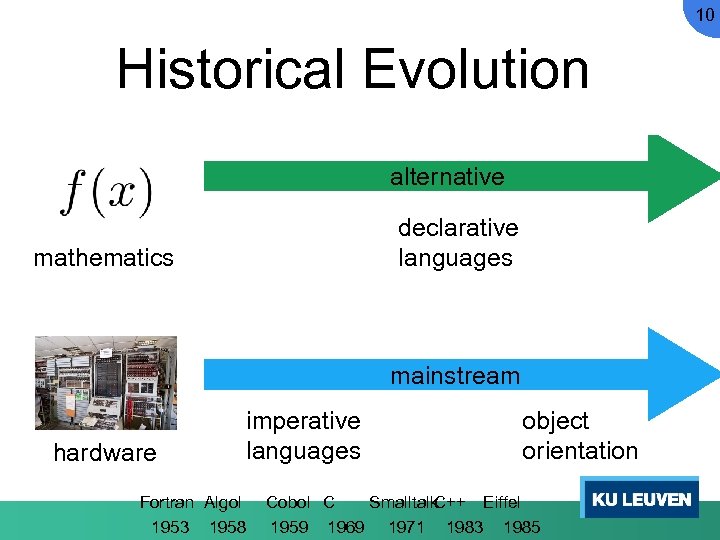10 Historical Evolution alternative declarative languages mathematics mainstream hardware imperative languages Fortran Algol 1953 1958 object orientation C++ Eiffel Cobol C Smalltalk 1959 1969 1971 1983 1985

11 Declarative Languages Functional Programming Haskell Constraint Programming Mini. Zinc Logic Programming Prolog

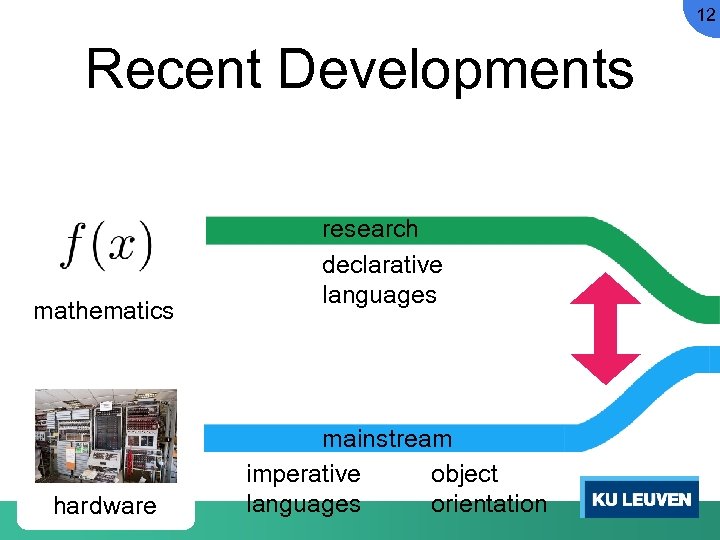12 Recent Developments mathematics hardware research declarative languages mainstream imperative object languages orientation

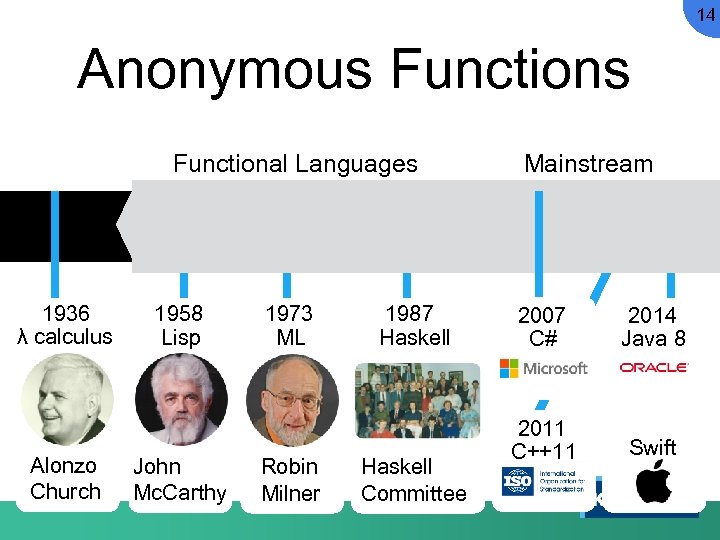14 Anonymous Functional Languages 1936 λ calculus Alonzo Church 1958 Lisp John Mc. Carthy 1973 ML Robin Milner 1987 Haskell Committee Mainstream 2007 C# 2014 Java 8 2011 C++11 Swift

Is there a doctor FP-programmer in the audience? 15/72

16 Early Adopters Haskell Language + GHC Compiler Finance Telecom Many Others

Productivy and Functional Programmin • http: //simontylercousins. net/does-the-language-you-usemake-a-difference-revisited/ • The problem 17/72

Solution in C# 18/72

Solution in F# 19/72

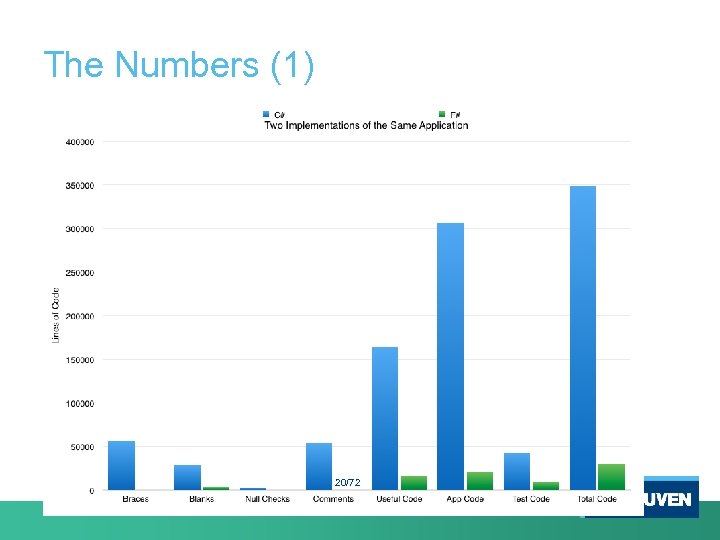The Numbers (1) 20/72

The Numbers (2) 21/72

The Numbers (3) 22/72

Rest of the presentation • Some concepts of Functional Programming o With examples in Haskell, F# and C# 23/72

Declarative Programming Describing the what instead of the how What • Derivation from ‘input’values to ‘output’-values • Or expressing properties o How • What machine to use • When to use which features of machine • What steps to set Often mathematically sound • (but still fun to do ; -) • Intelligent execution o • Programmer considered intelligent verifiable o 24 Mostly not verifiable

Declarative Programming Examples What = Expressions • SQL • Linq (mostly) • Logic Programming o How = Statements • Imperative programming • Manipulation of v ariables • What machine to use o Constraint Programming von Neumann architecture • When to use which • Functional Programming features of machine o Different mindset! Variables = registers • What steps to set o 25 o Order of execution Outer loops (for, while)

Logic Programming = Prolog (1 a) ancestor(x, y) : - parent(x, y). ancestor(x, y) : - ancestor(x, z), parent(z, y). female. Ancestor(x, y) : - ancestor(x, y), female(x). ? - female. Ancestor(Kris, Lars). ? - female. Ancestor(Celine, Lars). ? - female. Ancestor(x, Lars). 26/72 => no => yes => Celine, Liesbet

Logic Programming = Prolog (1 b) female(Celine). female(Liesbet). female(Hanne). male(Kris). male(Lars). parent(Celine, Kris). parent(Kris, Lars). parent(Liesbet, Lars). 27/72

Logic Programming = Prolog (2) even. Number([]). even([_, _|T]): - even. Number(T). palindrome(L): - reverse(L, L). reverse([], []). reverse([H|T], R): - reverse(T, T 1), append(T 1, [H], R). 28/72

(Pure) Functional Programming • Much closer to “real” programming o o Logic Programming = (partial) instantation = more magic Functional Programming • functions with parameters returning values • Much like functions and/or methodes • But o No side effects • Referential transparency • An expression is a value with always the same value • “no (hidden or far distant) state messing with things” • Strongly typed with type inference “Strongly typed programs can’t go wrong” 29/72 • Polymorf: a function can have many types o

Lambda calculus • Each expression has a never-changing-value o o z = 18 y = sin(z) • Complex expressions are calculated by evaluating and substituting subexpressions o (z + sin(z))*(y+cos(y)) • Function calls behave exactly the same o o o Always call by value Always return value No pointer- or out variables 30/72

Lambda Calculus (2) • f x = g(3+x)+x • g y = y+1 • z=5 • fz+gz 31/72

How to express new state? • Never o No mutable variables! (in pure FP-languages) • in general no side effects o Confusing for imperative programmers • F# allows for explicit declaration of mutable variables • C# allows for explicit declaration of readonly (instance) variables • But actually always o A new state is a new value • May be stored explicitly in a variable • Or may be stored temporarily in memory 32/72

Explicit new values! let y = a + b y. Plus 1 = y + 1 f x = (x+y)/y. Plus 1 in f a + f b No confusion between x++ and ++x etc. 33/72

Advantages of having no mutable variables • Referential transparancy A reference always refers to the same value o Mathematically sound • Implicit parallellism o Order of execution can be chosen, both at compile and run time o Synchronisation: locking issues when dependencies • Formal reasoning o Automated correctness and equivalence proofs o More transparant code o No underlying dependency from mutable states o 34/72

35 Side Effects Traditional Mainstream Languages Oops, unexpected interference

36 No Side Effects Traditional Declarative Languages Traditional Mainstream Languages No Side-Effects, No Problem No Side-Effects, No Party ✓ Mathematical Elegance ✓ Predictable ✓ No Interference

37 Explicit Side Effects State-of-the-Art Declarative Languages Explicit Side-Effects, No Problem ✓ Mathematical Elegance ✓ Predictable ✓ Explicit Interference

How to return many values? • Imperative programs Return 1 value from function o And others as ‘out’ parameters (using call by reference) • OO programs using only call by value o Define a container class for each combination of types o Cumbersome… o • FP-languages use tuples (x, y) , (x, y, z) , (a, b, c, d), … o o Flexible in number of elements Flexible in composing types 38/72

Recursion = “looping” (1) From definition to code n! = n*(n-1)! With base case 1! = 1 • Non-recursive C# • Haskell o o public long fac(int n) { long value = 1; for (int i=2; i<=n; n++) { value = value * i; } return value ; } fac 1 = 1 fac n = n * fac (n-1) 39

Recursion = “looping” (2) From definition to code n! = n*(n-1)! With base case 1! = 1 • F# • Recursive C# let rec fact x = if x < 1 then 1 else x * fact (x - 1) public long fac(int n) { if (n==1) return 1; return n * fac (n-1); } 40

Recursion = “looping” (3) Stack. Over. Flow error? • “Real” functional languages use more optimisation techniques for recursive programs • F# • Recursive C# let rec fact x = if x < 1 then 1 else x * fact (x - 1) public Big. Integer fac(int n) { if (n==1) return 1; return n * fac (n-1); } 41

Tail recursion Taking care of useless stack frames • Haskell • F# fac n = fac’ n 1 let fac n = fac. T n 1 fac‘ 1 acc = acc fac‘ n acc = fac’ (n-1) (n*acc) let rec fac. T n acc = if n = 1 then acc else fac. T (n-1) (n*acc) 42

Tail recursion (2) Taking care of useless stack frames • C# Big. Integer Factorial(int n, Big. Integer product) { if (n < 2) return product; return Factorial(n - 1, n * product); } 43

Exercises in my master class ; -) 1. Hermite sum 1/n + 1/(n-1)+… 1/2+1/1 2. Mysterious function (presumption of Fermat) Reduce n to 1 with the following steps o • • Odd n => continue with 3 n+1 Even n => continue with n/2 3. Calculate number. Of. Divisors and is. Priem 44/72

Solutions in Haskell herm 1 = 1 herm n = 1/n + (herm (n-1)) myst 1 = [1] myst n | mod n 2 == 0 | otherwise = n: (myst (div n 2)) = n: (myst (3*n+1)) number. Of. Divisors … is. Prime n = (number. Of. Divisors n) == 2 45/72

Recursive Programming: conclusion • Not exclusively for functional programming • But very typical for FP o And efficient • Interesting pattern also for non FP-languages! 46/72

Lists in Functional Programming • Omnipresent feature o o In most languages But very strong support in FP • Especially when combined with pattern matching • And recursive programming • Remember basic concept of recursion: Define primitive/base expression(s) Reduce complex expression to more simple expression 1. 2. • • N reduces to n-1, n/2, … List reduces to list with fewer elements 47/72

Pattern matching in Haskell fac 1 = 1 fac n = n * fac (n-1) find. Value [] y = False find. Value (x: xs) y = if x == y then True else find. Value xs y even. Elems [] = True even. Elems [x] = False even. Elems (x: y: ys) = even. Elems ys 48/72

Pattern matching in F# find. Value [] y = False find. Value (x: xs) y = if x == y then True else find. Value xs y let rec find. Value list x = match list with | [] -> False | y: : ys -> if x == y then True else find. Value x ys 49/72

Pattern Matching in C# • Proposition for Roslyn in 8/2014 o o https: //roslyn. codeplex. com/discussions/560339 http: //www. infoq. com/news/2014/08/Pattern-Matching if (expr is Type v) { // code using v } // try-cast var c = Cartesian(3, 4); if (c is Polar(var R, *)) Console. Write. Line(R); var a = new Location(1, 2, 3); //x=1, y=2, z=3 50/72 if (a is Location(1, var y, *))

Defining (recursive) types in Haskell • • • data Examenvorm = M | S | P data Sexe= M | V data Human = Mens Integer String Geslacht data Point = Point Integer data Generic. Point a = Pt a a data Tree a = Leaf a | Branch (Tree a) • Perfect for pattern matching! 51/72

Defining (recursive) types (2) • Comparable to structs and even classes • data Human = Human { age : : Integer, name : : String, sexe : : Sexe } • Creates automatically the following functions o o Human : : Integer -> String -> Sexe -> Human age : : Human -> Integer name : : Human -> String sexe : : Human -> Sexe 52/72

Insert sort in Haskell isort [ ] = [ ] isort (x: xs) = insert x (isort xs) insert x [ ] = [x] insert x (y: ys) = if (x

Insert sort in F# let rec insert x l = match l with | [] -> [x] | y: : ys -> if x <= y then x: : ys else y: : insert x ys and insertsort l = match l with | [] -> [] | x: : xs -> insert x (insertsort xs) Source: http: //www. codex. com/wiki/Insertion_sort 54/72

Insert sort in C# (non-functional) static void Insert. Sort(IComparable[] array) { int i, j; for (i = 1; i < array. Length; i++) { IComparable value = array[i]; j = i - 1; while ((j >= 0) && (array[j]. Compare. To(value) > 0)) { array[j + 1] = array[j]; j=j-1; } array[j + 1] = value; } } 55/72

Type Classes and type inference • Note the explicit IComparable[] array in function type o static void Insert. Sort(IComparable[] array) • In Haskell implicit and auto-detected 56/72

Polymorfic: look at the types • Typ “: i isort” at command prompt of Haskell Interpreter o isort : : Ord a => [a] -> [a] • Similar o o o half. List : : [a] -> [a] find. Value : : Eq a => [a] -> a -> Bool fac : : (Num a, Eq a) => a -> a 57/72

Strongly typed programs can’t go wrong • Type inference tries to find the most general type of function o Depending on the functions that are being used • Programmer doesn’t need to define types o o o But a type mismatch results in a compile time error Indicating a mistake in the reasoning Whenever type inference succeeds most programs run correctly 58/72

Type inference in. NET • More and more available 59/72

List Comprehensions in Haskell Very declarative constructor -- give all even numbers of a list evens list = [x | x <- list, even x] in. Both list 1 list 2 = [x | x <- list 1, find. Value x list 2] combine list 1 list 2 = [(x, y) | x <- list 1, y <- list 2] 60/72

List Comprehensions in Haskell Very declarative constructor -- give all even numbers of a list evens list = [x | x <- list, even x] in. Both list 1 list 2 = [x | x <- list 1, find. Value x list 2] combine list 1 list 2 = [(x, y) | x <- list 1, y <- list 2] 61/72

List Comprehensions in F# [for x in collection do. . . yield expr] seq { for x in 0. . 100 do if x*x > 3 then yield 2*x } ; ; evens list = [x | x <- list, even x] in. Both list 1 list 2 = [x | x <- list 1, find. Value x list 2] combine list 1 list 2 = [(x, y) | x <- list 1, y <- list 2] 62/72

List Comprehensions in C# from x in Enumerable. Range(0, 100) where x * x > 3 select x * 2 63/72

Quicksort: even more beautiful ; -) • Concept of quicksort 1. 2. Take “a” element of the list: the “spil” Split the list in two 1. Elements smaller than spil 2. Elements bigger than spil 3. 4. Quicksort each sublist (recursively ; -) Join the sorted lists together 64/72

Quicksort in Haskell qsort [] = [] qsort [x] = [x] qsort (x: xs) = let smaller = qsort([y | y <- xs, y < x]) larger = qsort([y | y <- xs, y > x]) in smaller ++ (x: larger) 65/72

Quicksort in F# let rec qsort: int list -> int list = function | [] -> [] | x: : xs -> let smaller = [for a in xs do if a<=x then yield a] let larger = [for b in xs do if b>x then yield b] qsort smaller @ [x] @ qsort larger let rec qsort = function | [] -> [] | x: : xs -> let smaller, larger = List. partition (fun y -> y<=x) xs qsort smaller @ [x] @ qsort larger 66/72

Higher order functions • Functions taking other functions as parameters • Simple list functions map & filter map fac [3, 6, 2, 4] o filter odd [1, 2, 3, 4, 5, 6, 7] • More Complex list functies foldr & foldl o Reduce a list to one value o • Using a combining function • And a starting value o Foldr (+) 0 [1, 2, 3, 4, 5, 6] 67/72

Recursion over functions repeat. Fun 0 f value = value repeat. Fun n f value = repeat. Fun (n-1) f (f value) bubble. Sort list = repeat. Fun(length list) bubble list bubble [] = [] bubble [x] = [x] bubble (x: y: ys) | x < y = x: (bubble (y: ys)) | otherwise = y: (bubble (x: ys)) 68/72

Anonymous functions • Lambda abstractions 69/72

Currying • Functions of n arguments • Are actually functions of 1 argument o Returning a function of (n-1) argument • Which is actually of function of 1 argument • Returning a function of (n-2) arguments - … • Specialisation of functions contains 2 = contains 2 70/72

Open your mind! • Become a Better Developer with Functional Programming o http: //www. oscon. com/oscon 2011/public/schedule/detail /19191 Questions? 71/72

More info about the TETRA-project? • http: //www. vlambda. be/ • Contact Kris. Aerts@kuleuven. be or Tom Schrijvers . NET-productiviteit verhogen met een gepast gebruikt van lambda's en F# (en natuurlijk ook in Java ; -) Vlaamse software vlamt met lambda’s 72/72