Fully Anonymous Group Signatures without Random Oracles Jens

Fully Anonymous Group Signatures without Random Oracles Jens Groth University College London

Agenda • Introduction – Group signatures – Full anonymity – Previous work and our results • Generic construction – – Certified signatures Anonymization through NIZK proofs Opening through CCA 2 -secure encryption Generic group signature • Pairing-based construction – – GS proofs BB signatures and ZL certificates Tag-based CCA 2 -secure encryption Our group signature

Issuer Member Anonymous signature Group

Issuer Opener Group manager Group signature Group

Anonymity? • Can group signatures made by the same member be linked? • What happens if somebody loses his secret group membership key, are all his signatures suddenly identifiable? • What happens if somebody gets the opener to trace the signers of selected group signatures? (think chosen ciphertext attack)

Full anonymity Issuer is corrupt All members’ group signature keys are exposed Opener is honest (otherwise anonymity not possible) but willing to open group signatures • Two honest members’ group signatures on the same message are indistinguishable Unlinkable, key-exposure resilient, CCA-anonymous

Agenda • Introduction – Group signatures – Full anonymity – Previous work and our results • Generic construction – – Certified signatures Anonymization through NIZK proofs Opening through CCA 2 -secure encryption Generic group signature • Pairing-based construction – – GS proofs BB signatures and ZL certificates Tag-based CCA 2 -secure encryption Our group signature

Previous work • Many papers [ACJT 00, CL 02, CL 04 BBS 04, CG 04, FI 05, KY 05, etc. ] Random oracle model • Boyen, Waters 06, 07 CPA-anonymous • Ateniese, Camenisch, Hohenberger, de Medeiros 06 Key-exposure • Bellare, Micciancio, Warinschi 03 Bellare, Shi, Zhang 05 Groth 06 Fully anonymous inefficient group signatures

Our contribution • • Fully anonymous group signature Separate Issuer and Opener Partially dynamic – the group can grow Efficient Group signature is around 2 k. B 50 group elements from elliptic curve • Based on bilinear groups Decisional linear assumption [BBS 04] More efficient schemes exist in the q-Strongrandom oracle model Diffie Hellman assumption [BB 04] q-Unfakeability assumption [ZL 06]

Agenda • Introduction – Group signatures – Full anonymity – Previous work and our results • Generic construction – – Certified signatures Anonymization through NIZK proofs Opening through CCA 2 -secure encryption Generic group signature • Pairing-based construction – – GS proofs BB signatures and ZL certificates Tag-based CCA 2 -secure encryption Our group signature

New member joining the group Issuer Member Signature key pair: (vk, sk) Issuer’s certificate on vk: cert

Signature – not anonymous cert, vk, signsk(m) Member

Anonymous signature NIZK(cert, vk, signsk(m)) Member Non-interactive zero-knowledge proof of knowledge of (cert, vk, signsk(m)) - guarantees certified signature exists - reveal nothing about contents

Anonymous signature NIWI(cert, vk, signsk(m)) Member Non-interactive witness-indistinguishable proof of knowledge of (cert, vk, signsk(m)) - guarantees certified signature exists - does not reveal signer

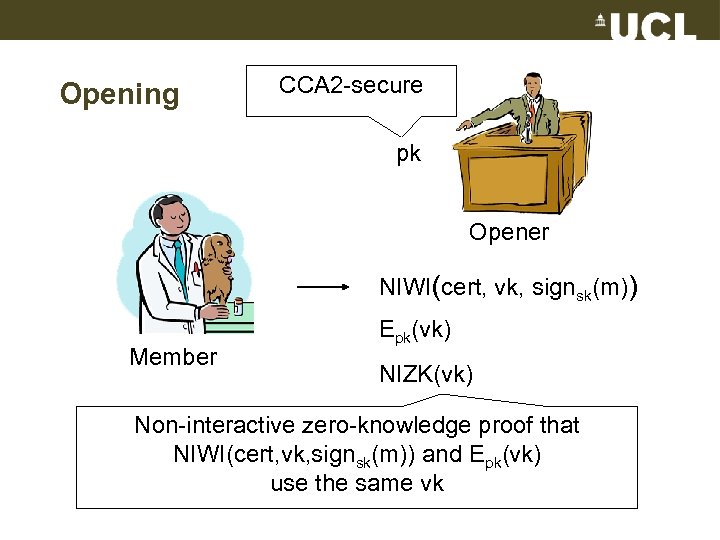Opening CCA 2 -secure pk Opener NIWI(cert, vk, signsk(m)) Member Epk(vk) NIZK(vk) Non-interactive zero-knowledge proof that NIWI(cert, vk, signsk(m)) and Epk(vk) use the same vk

Group signature vksots NIWI(cert, vk, signsk(m)sots)) (vk ) Member Epk(vk) NIZK(vk) Signsots(vksots, m, NIWI, E, NIZK) Strong one-time signature on message and everything else

Agenda • Introduction – Group signatures – Full anonymity – Previous work and our results • Generic construction – – Certified signatures Anonymization through NIZK proofs Opening through CCA 2 -secure encryption Generic group signature • Pairing-based construction – – GS proofs BB signatures and ZL certificates Tag-based CCA 2 -secure encryption Our group signature

Bilinear groups • • Prime p Groups G, GT of order p g generates G Bilinear map e: G × G → GT - e(g, g) generates GT - e(ga, gb) = e(g, g)ab • Efficiently computable group operations, group membership, bilinear map, etc.

GS proofs [Groth, Sahai 06] Efficient NIZK and NIWI proofs for bilinear-group statements Statements of the form x, y, z, . . . G φ, θ, . . . Zp e(a, x) e(y, z) = T bφ y 5θ+2 z = t 3φ + 2φθ = 8 mod p Security based on Decisional Linear Assumption

Agenda • Introduction – Group signatures – Full anonymity – Previous work and our results • Generic construction – – Certified signatures Anonymization through NIZK proofs Opening through CCA 2 -secure encryption Generic group signature • Pairing-based construction – – GS proofs BB signatures and ZL certificates Tag-based CCA 2 -secure encryption Our group signature

Signature BB signature [Boneh, Boyen 04] vk = gsk signsk(m) = g 1/(sk+m) Verify e(sig, gmvk) = e(g, g) Use BB signature for both vksots, signsots(vk, m, NIWI, E, NIZK) vk, signsk(vksots) Security based on q-Strong Diffie Hellman Assump.

Certified signature Certificate [Zhou, Lin 06] Public issuer key: f, h G , T GT Certificate on vk: (a, b) so e(a, hvk) e(f, b) = T Certified in combination with BB Unforgeablesignature Forgeable! signature [Boldyreva, Fischlin, VK = vk 2 h. Hellman and Palacio, Security based on q-Strong Diffie. Warinschi 07] e(a 1/2, h. VK) e(f, b) = T Hard to assumptions q-Unfakeabilityforge both certificate and signature at the same time

Agenda • Introduction – Group signatures – Full anonymity – Previous work and our results • Generic construction – – Certified signatures Anonymization through NIZK proofs Opening through CCA 2 -secure encryption Generic group signature • Pairing-based construction – – GS proofs BB signatures and ZL certificates Tag-based CCA 2 -secure encryption Our group signature

Selective-tag weak CCA-secure encryption Instead of full-blown CCA 2 -secure encryption, use selective-tag weak CCA-secure encryption [Kiltz 06] We use tag = hash(vksots) pk = (F, H, K, L) Epk(tag, m) = ( Fr, Hs , gr+sm , (gtag. K)r , (gtag. L)s ) Security based on the Decisional Linear Assumption

Agenda • Introduction – Group signatures – Full anonymity – Previous work and our results • Generic construction – – Certified signatures Anonymization through NIZK proofs Opening through CCA 2 -secure encryption Generic group signature • Pairing-based construction – – GS proofs BB signatures and ZL certificates Tag-based CCA 2 -secure encryption Our group signature

Fully anonymous group signature vksots NIWI(cert, vk, signsk(vksots)) tag=vksots Epk(tag, vk) NIZK(same vk) signsots(m, above) BB-key certified sign. [ZL] + GS proof Use bilinear groups for all tools to get efficient NIWI and NIZK proofs Group signature size 50 group elements from elliptic curve Kiltz-encryption GS-proof BB-signature

Thank you • Conclusion – – – Pairing based group signature Fully anonymous Separate Issuer and Opener Partially dynamic group Size: 50 elements from elliptic curve Standard type cryptographic assumptions (no random oracles)