From Punched Cards to Modular and Multilayer Modeling

From Punched Cards to Modular and Multilayer Modeling – Forty Years of Computer Based Problem Solving in Chemical Engineering. Part II. Mordechai Shacham Department of Chemical Engineering Ben-Gurion University of the Negev Beer-Sheva, Israel May 21, 2012

Semi-Batch Distillation - Problem Statement Consider the semi-batch steam distillation of an n-octane (comp. 1) and n-decane (comp. 2) mixture. The data provided by Ingham et al. are the following. Initially M = 0. 015 kmol of organics with composition x 1 = 0. 725 is charged into the still. The initial temperature in the still is T 0 = 25 °C. Starting at time t = 0, steam at a temperature Tsteam = 99. 2 °C is bubbled continuously through the organic phase at the rate of MS = 3. 85 e 5 kmol/s. All the steam is assumed to condense during the heating period. The ambient temperature is TE = 25 °C and the heat transfer coefficient between the still and the surrounding is U = 1. 05 J/s-K. The ambient pressure is P = 9. 839 E+04 Pa.

Semi-Batch Distillation - Problem Statement a. Calculate and plot the still temperature (T), component mole fractions inside the still (x 1, x 2, y 1, and y 2) and the component mole fractions in the distillate (x 1 dist and x 2 dist) using the data and the initial values provided. b. Determine the lowest n-octane mole fraction in the feed that can yield a distillate concentration of 90% of n-octane. Compute the percent recovery of n-octane in the distillate as function of its concentration in the feed. Vary the feed concentration in the range where the requirement for the n-octane concentration in the distillate is attainable. Reference: Shacham et al. "Semi-Batch Steam Distillation of a Binary Organic Mixture ", Chem. Eng. Edu. , In press (2012)

Semi-Batch Distillation - Heating Period Equations Mass balance on the water phase yields Stopping Criterion

Semi-Batch Distillation - Distillation Period Equations Solving with Polymath the “controlled integration technique” is used for adjusting the temperature to follow the bubble point curve where

Semi-Batch Distillation - Physical Property Needs and Sources for the Original Reference* *Prenosil, J. E. , Chem. Eng. J. 12, 59 -68 (1976)

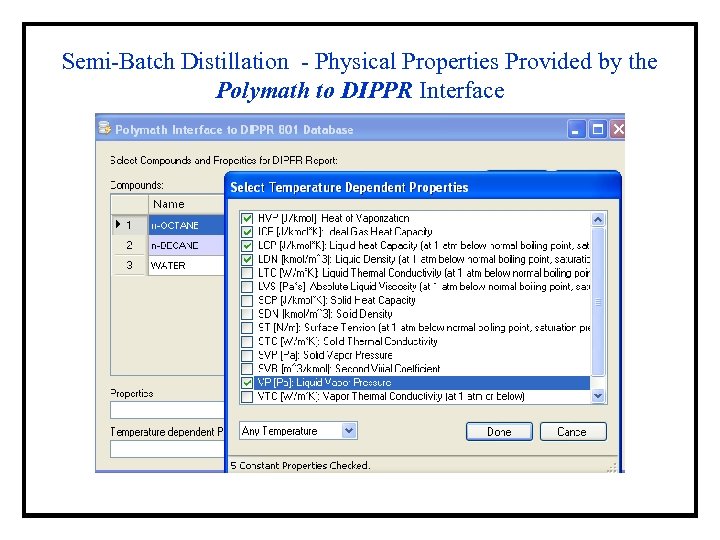Semi-Batch Distillation - Physical Properties Provided by the Polymath to DIPPR Interface

Semi-Batch Distillation - Physical Properties Provided by the Polymath to DIPPR Interface Unique variable name Units and uncertainty in comments Valid temperature range Ideal gas enthalpy equation in a “comment”

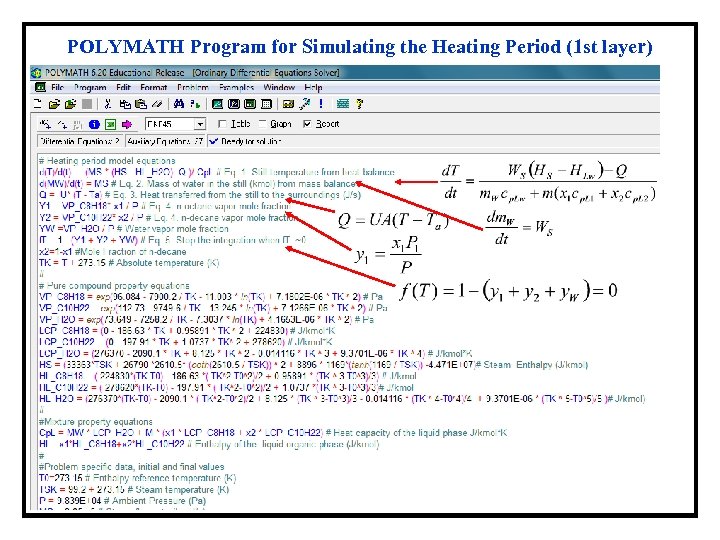POLYMATH Program for Simulating the Heating Period (1 st layer)

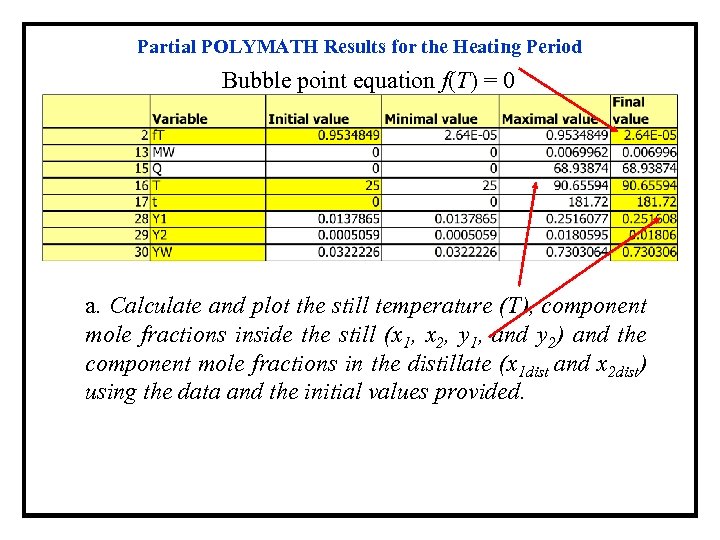Partial POLYMATH Results for the Heating Period Bubble point equation f(T) = 0 a. Calculate and plot the still temperature (T), component mole fractions inside the still (x 1, x 2, y 1, and y 2) and the component mole fractions in the distillate (x 1 dist and x 2 dist) using the data and the initial values provided.

POLYMATH Program for Simulating the Distillation Period ( 1 st layer) Following the bubble point curve with controlled integration

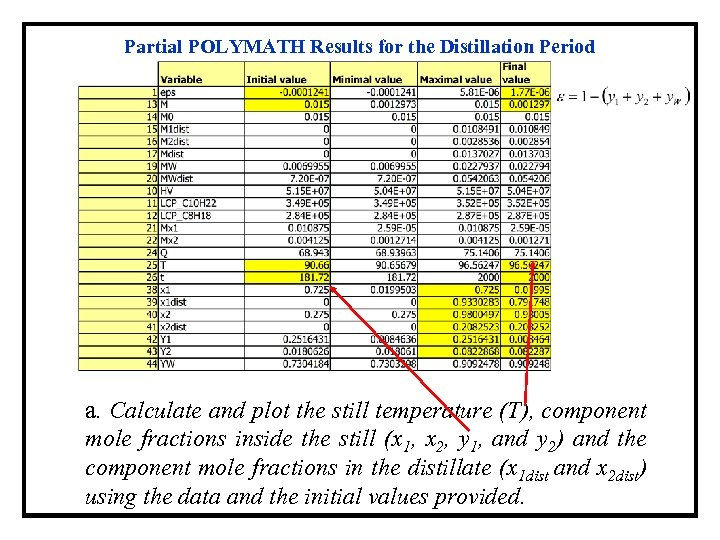Partial POLYMATH Results for the Distillation Period a. Calculate and plot the still temperature (T), component mole fractions inside the still (x 1, x 2, y 1, and y 2) and the component mole fractions in the distillate (x 1 dist and x 2 dist) using the data and the initial values provided.

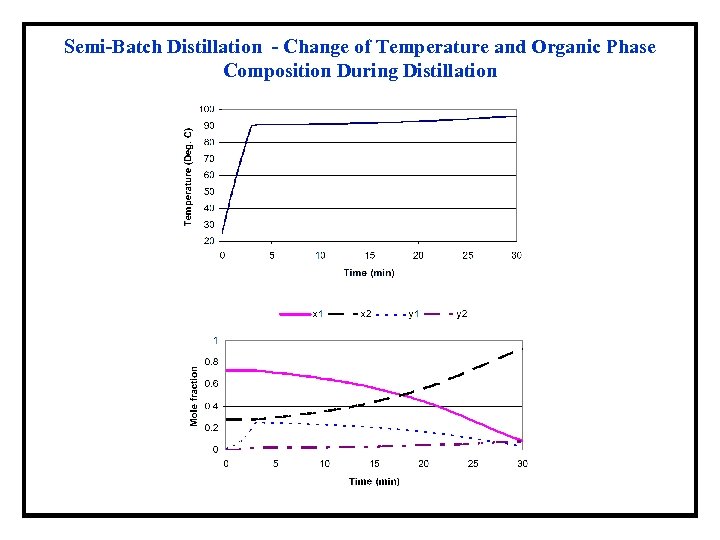Semi-Batch Distillation - Change of Temperature and Organic Phase Composition During Distillation

Polymath Generated MATLAB Formatted Model the Distillation Period

MATLAB Main Program – Heating Period Calculations for Various Initial n-octane Mole Fractions Upper layer 2 nd layer 1 st layer

MATLAB Main Program – Distillation Period Calculations 2 nd layer

Distillation Period Calculations – Converting the Differential Equations to Implicit Algebraic Equations for solving the DEA System

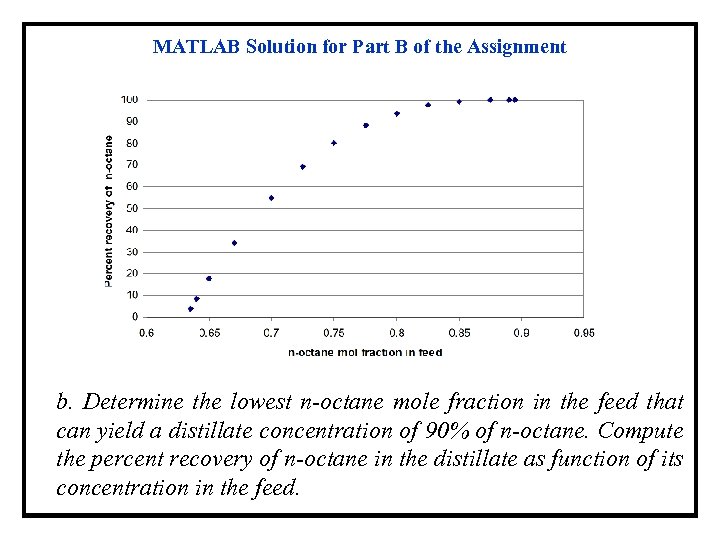MATLAB Solution for Part B of the Assignment b. Determine the lowest n-octane mole fraction in the feed that can yield a distillate concentration of 90% of n-octane. Compute the percent recovery of n-octane in the distillate as function of its concentration in the feed.

Conclusions In the ~25 years of the use of the mathematical software packages they have essentially replaced all the traditional problem solving techniques for SMSA problems. The modular multilayer technology presented here enables students to progress gradually, as they gain more experience in modeling, into solution of more complex MMSA, SMMA and MMMA problems. In addition to reducing the time and effort required for building the process models, the proposed approach yields modular programs that are well documented and easily modified. State of the art modeling requires the use of property databases which provide up to date property data with validated uncertainty and temperature range of applicability values

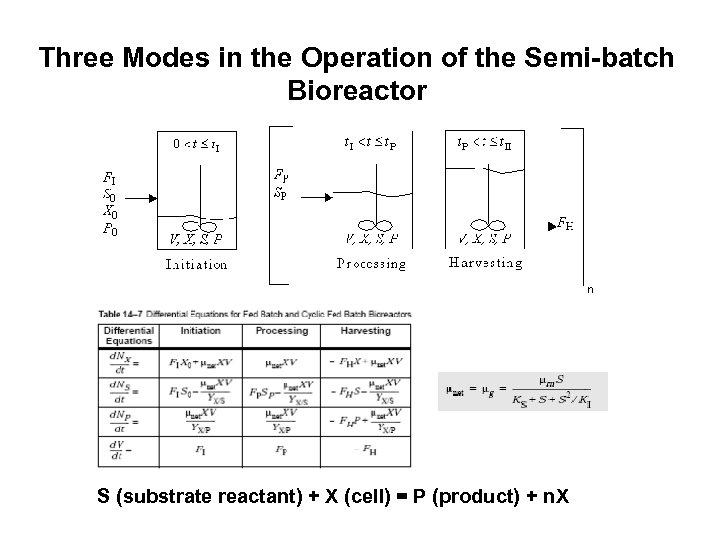Three Modes in the Operation of the Semi-batch Bioreactor S (substrate reactant) + X (cell) = P (product) + n. X

Three Modes in the Operation of the Semi-batch Bioreactor Substrate feed rate FI Substrate feed rate FP Discharge flow rate FH Final volume VI Final Volume VH Final Volume VI S (substrate reactant) + X (cell) = P (product) + n. X The biochemical reaction is inhibited by the substrate Optimal substrate feed concentration is required with fixed set of operating conditions n – cycle number n = 1 fedbatch operation

POLYMATH Model for the Initiation Mode of the Semi-batch Bioreactor

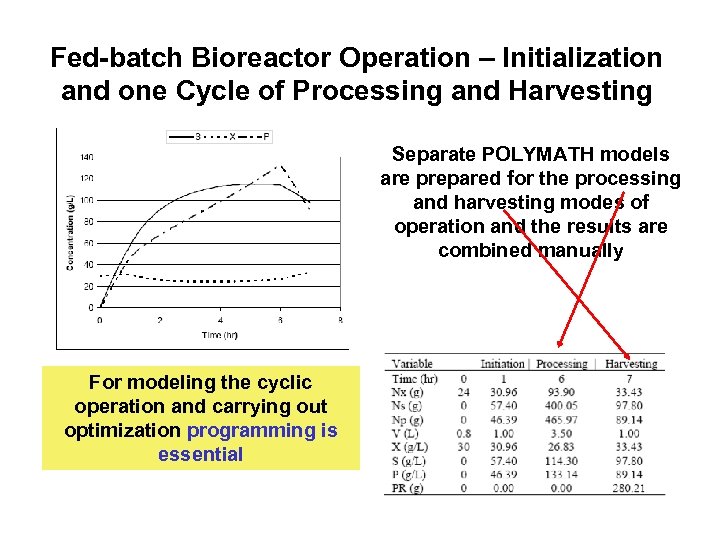Fed-batch Bioreactor Operation – Initialization and one Cycle of Processing and Harvesting Separate POLYMATH models are prepared for the processing and harvesting modes of operation and the results are combined manually For modeling the cyclic operation and carrying out optimization programming is essential

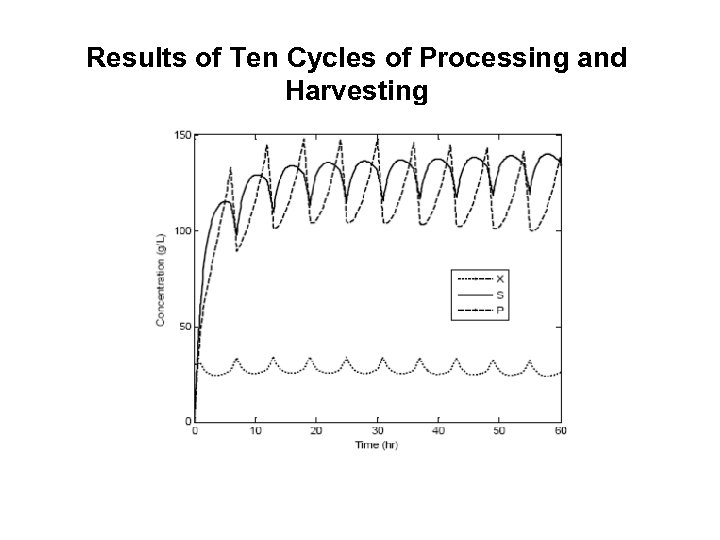Results of Ten Cycles of Processing and Harvesting

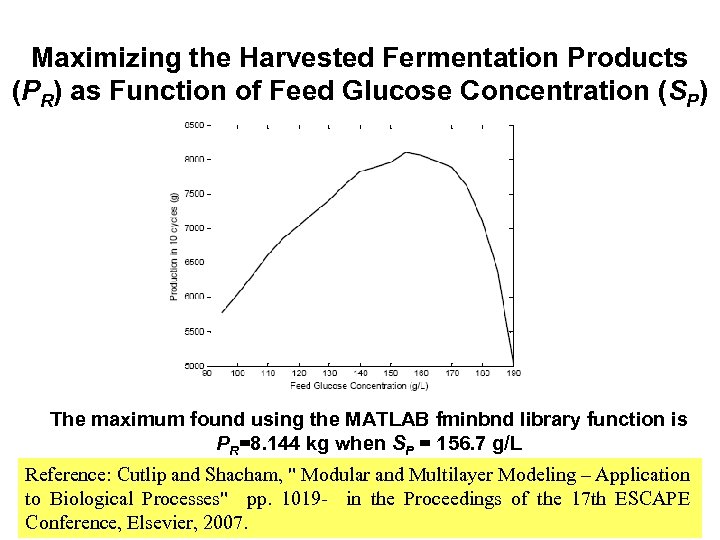Maximizing the Harvested Fermentation Products (PR) as Function of Feed Glucose Concentration (SP) The maximum found using the MATLAB fminbnd library function is PR=8. 144 kg when SP = 156. 7 g/L Reference: Cutlip and Shacham, " Modular and Multilayer Modeling – Application to Biological Processes" pp. 1019 - in the Proceedings of the 17 th ESCAPE Conference, Elsevier, 2007.

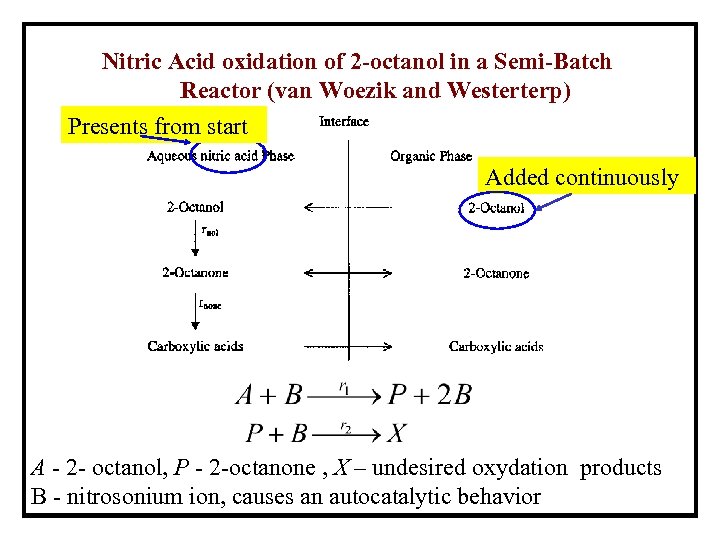Nitric Acid oxidation of 2 -octanol in a Semi-Batch Reactor (van Woezik and Westerterp) Presents from start Added continuously A - 2 - octanol, P - 2 -octanone , X – undesired oxydation products B - nitrosonium ion, causes an autocatalytic behavior

Semi-batch Reactor Model Representation in Polymath Format (3) Critical Parameters Reference: Eizenberg et al. "Combining HAZOP with Dynamic Simulation Applications for Safety Education", Journal of Loss Prevention in the Process Industries 19, 754– 761(2006)

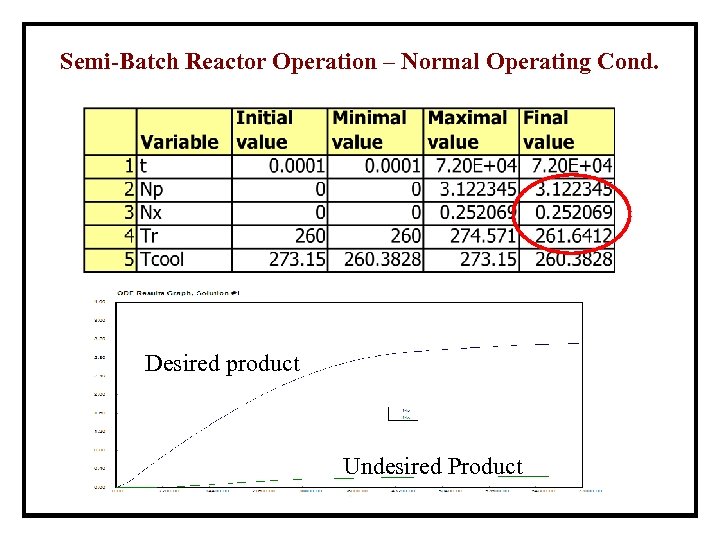Semi-Batch Reactor Operation – Normal Operating Cond. Desired product Undesired Product

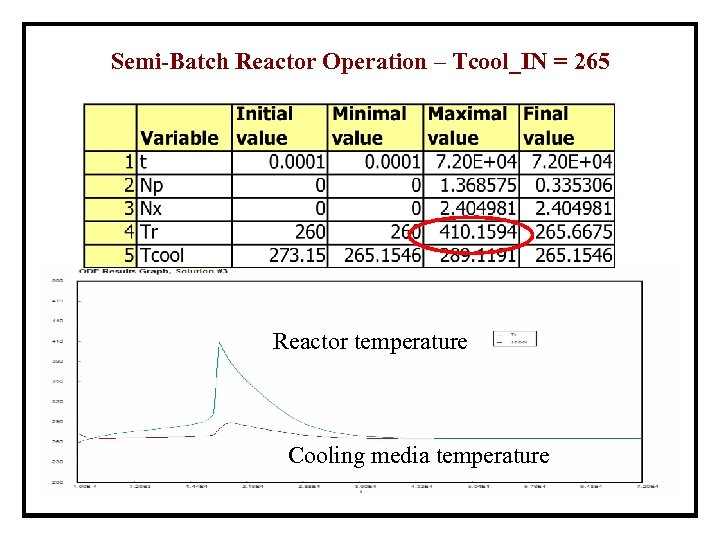Semi-Batch Reactor Operation – Tcool_IN = 265 Reactor temperature Cooling media temperature

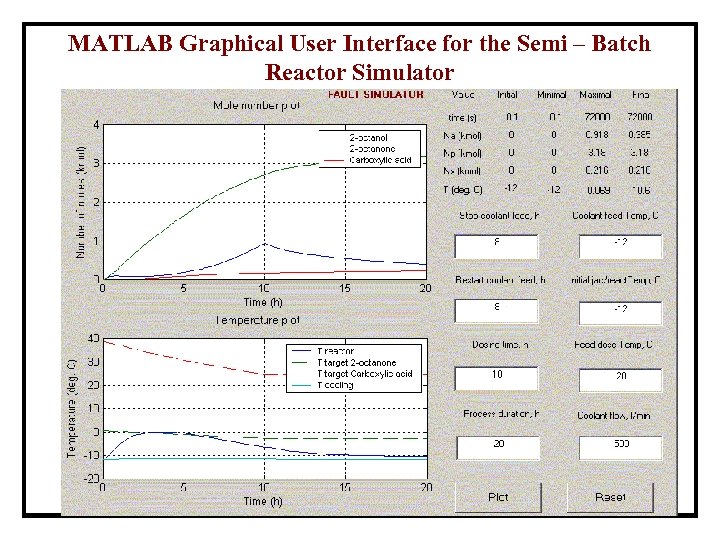MATLAB Graphical User Interface for the Semi – Batch Reactor Simulator

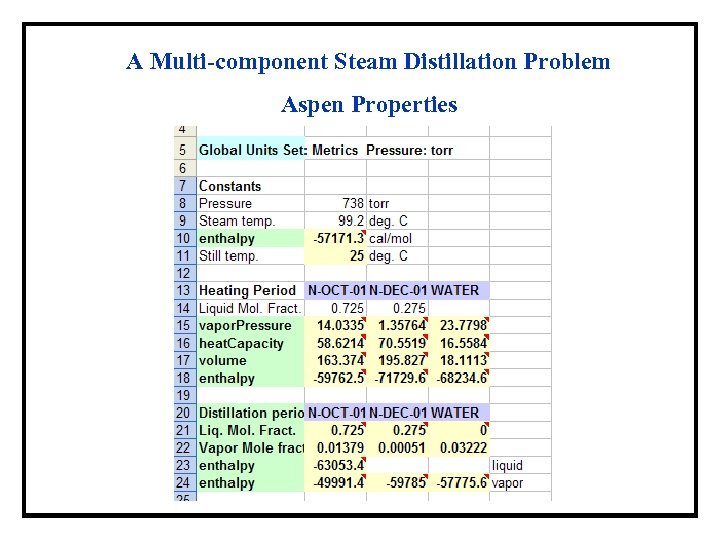A Multi-component Steam Distillation Problem Aspen Properties

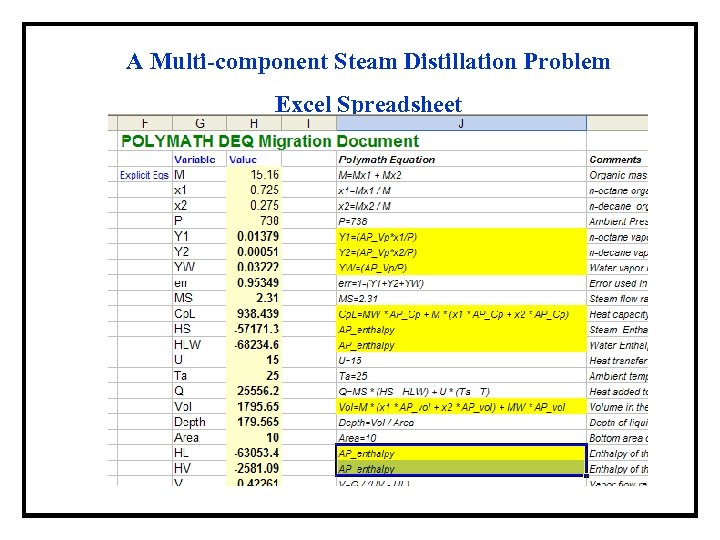A Multi-component Steam Distillation Problem Excel Spreadsheet

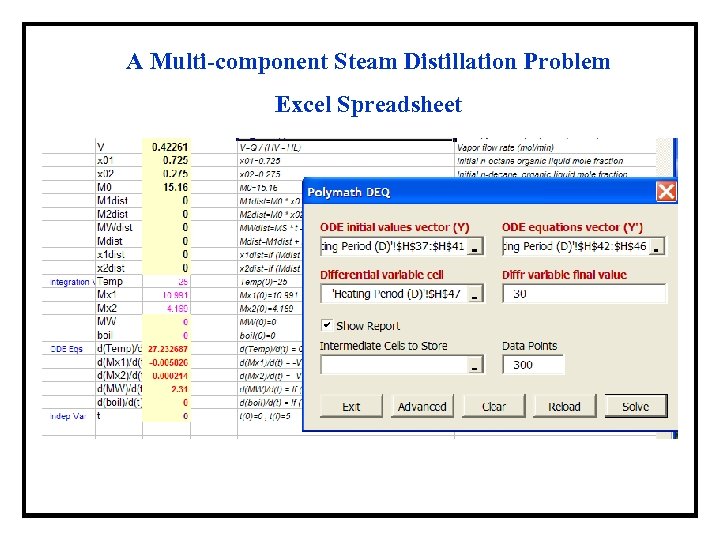A Multi-component Steam Distillation Problem Excel Spreadsheet