From Numerical Problem Solving to Model Based Experimentation

From Numerical Problem Solving to Model Based Experimentation – Incorporating Computer Based Tools of Multiscale Modeling into the Ch. E Curriculum Mordechai Shacham Chem. Eng. Dept. , Ben-Gurion University, Beer-Sheva 84105, Israel Michael B. Cutlip Chem. Eng. Dept. , University of Connecticut, Storrs, CT 06269, USA Neima Brauner Faculty of Engineering, Tel-Aviv University, Tel-Aviv, 69978, Israel

Description of the Engineer’s Main Tasks* Engineers are fundamentally problem solvers, seeking to achieve some objective or design among technical, social economic, regulatory and environmental constraints. *Edgar, T. F. , ASEE Presentation, Salt Lake City, UT, 2004

The Computer as a Problem Solving Tool – The Early Days ØComputer language (Fortran, Pascal, C) programming ØUse of programs prepared by the instructor and included in textbooks for problem solving (Henley and Rosen, Material and Energy Balance Computation, 1969). ØUse of flowsheeting programs (CHESS, Flowtran, etc. ) in a few courses. ØUse of dynamic modeling languages (CSMP) in “process dynamics and control” courses.

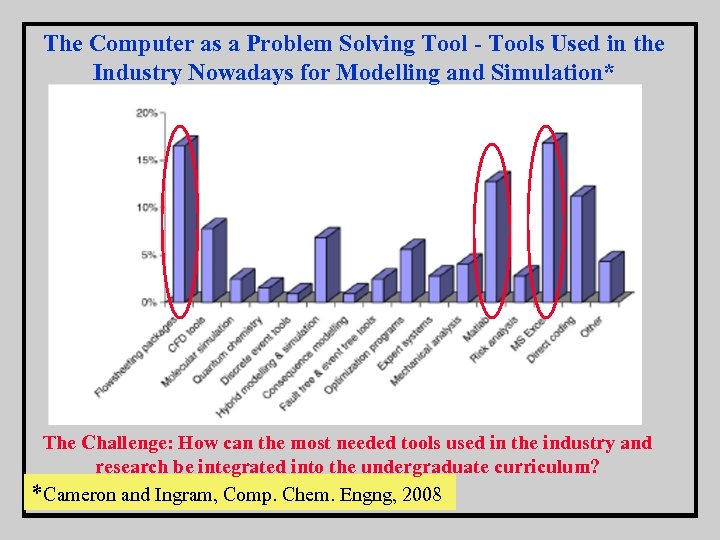
The Computer as a Problem Solving Tool - Tools Used in the Industry Nowadays for Modelling and Simulation* The Challenge: How can the most needed tools used in the industry and research be integrated into the undergraduate curriculum? *Cameron and Ingram, Comp. Chem. Engng, 2008

Presentation Outline - Incorporating Computer Based Tools of Multiscale Modeling into the Ch. E Curriculum Solution of Single-Model, Single-Algorithm (SMSA) Problems An Introductory Course on Computer Based Problem Solving Solution of Multiple-Model, Multiple-Algorithm (MMMA) Problems. Example: Optimization of a Bioreactor Operating in a Cyclic Mode Use of Data Bases and Large Scale Programs in Mini-Projects in Various Courses Use of Large Scale Programs and Instructor Prepared Demonstration Programs for Model-Based and Virtual Experimentation and Visualization

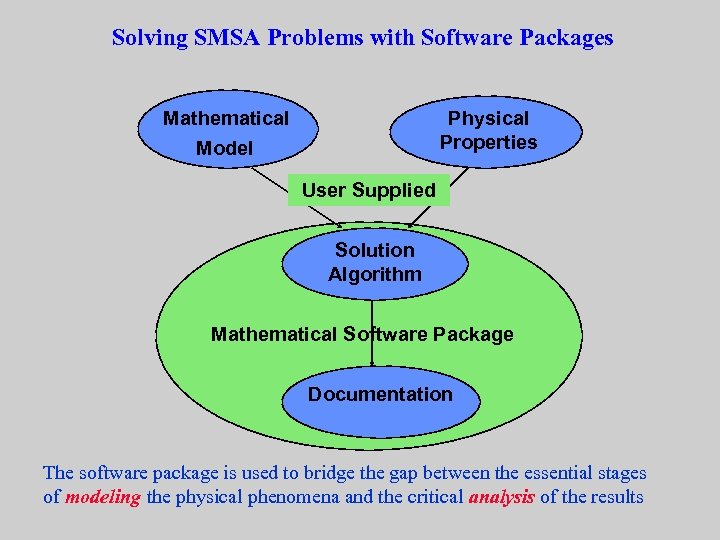
Solving SMSA Problems with Software Packages Mathematical Physical Properties Model User Supplied Solution Algorithm Mathematical Software Package Documentation The software package is used to bridge the gap between the essential stages of modeling the physical phenomena and the critical analysis of the results

A Single-Model, Single-Algorithm Problem (ODE) - Adiabatic Operation of a Tubular Reactor for Cracking of Acetone The irreversible, vapor-phase cracking of acetone (A) to ketene (B) and methane (C) that is given by the reaction: CH 3 COCH 3→CH 2 CO + CH 4 is carried out adiabatically in a tubular reactor. The reaction is first order with respect to acetone and the specific reaction rate can be expressed by The acetone feed flow rate to the reactor is FA mol/s, the inlet temperature is T = 1150 K and the reactor operates at the constant pressure of P = 162 k. Pa (1. 6 atm). The volume of the reactor is V = 4 m 3. Inert gas (nitrogen) is fed at the rate of FN mol/s.

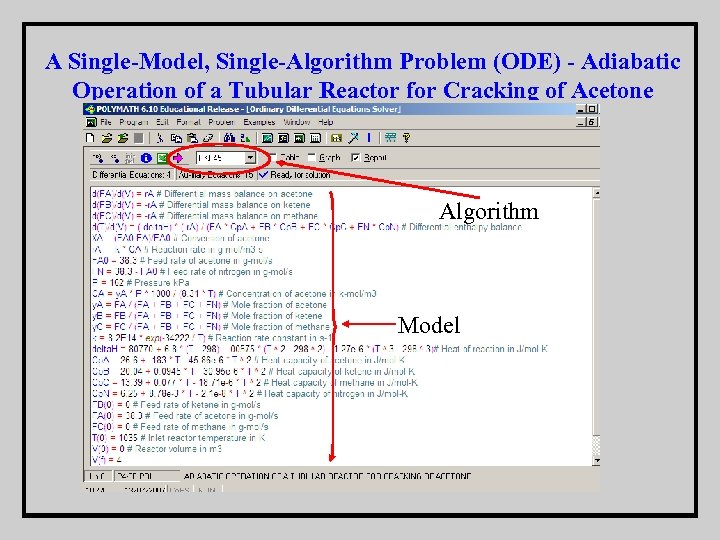
A Single-Model, Single-Algorithm Problem (ODE) - Adiabatic Operation of a Tubular Reactor for Cracking of Acetone Algorithm Model

A Single-Model, Single-Algorithm Problem (NLE) Complex Chemical Equilibrium The following reactions are taking place in a constant volume, gas-phase batch reactor: A system of algebraic equations describes the equilibrium of the preceding reactions. The nonlinear equilibrium relationships utilize thermodynamic equilibrium expressions, and the linear relationships have been obtained from the stoichiometry of the reactions.

A Single-Model, Single-Algorithm Problem (NLE) Complex Chemical Equilibrium The equilibrium coefficients KC 1, KC 2 and KC 3 can be expressed as function of the temperature (T) as where T is the temperature (K) the coefficients KC 1 and KC 2 are dimensionless, KC 3 has units of L/g-mol.

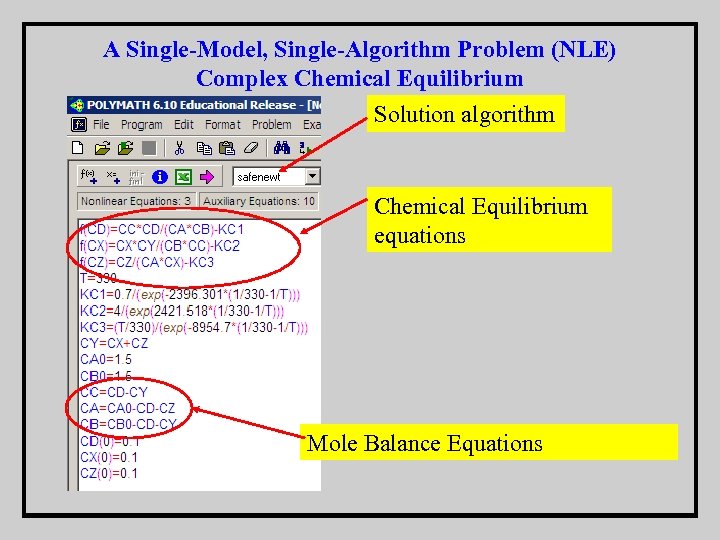
A Single-Model, Single-Algorithm Problem (NLE) Complex Chemical Equilibrium Solution algorithm Chemical Equilibrium equations Mole Balance Equations

POLYMATH – A Friendly Solver for SMSA Problems, Serves Also as a Ladder in Climbing to More Complex Tools and Tasks. Ø Nonlinear Equations - up to 300 simultaneous nonlinear and 300 explicit algebraic equations Ø Differential Equations - up to 300 simultaneous ordinary differential and 300 explicit algebraic equations Ø Data analysis and Regression - up to 1200 data points with capabilities for linear, multiple linear, and nonlinear regressions Ø Automatic Migration of Models to Excel Ø Generation of MATLAB functions of the Models

POLYMATH – A Long History in Engineering Computations

Problem Solving in Chemical and Biochemical Engineering Chapters CBPS Course 1. Introduction 2. Basic Principles and Calculations 3. Regression and Correlation of Data 4. Problem Solving with Excel 5. Problem Solving with MATLAB 6. Advanced Techniques in Problem Solving. Subject Matter Specific Examples 7. Thermodynamics 8. Fluid Mechanics 9. Heat transfer 10. Mass Transfer 11. Chemical Reaction Engineering 12. Phase Equilibria and Distillation 13. Process Dynamics and Control 14. Biochemical Engineering

Contents of the Computer-Based Problem Solving Course 1. Introduction 2. Historical perspective on problem solving 3. Categorizing problems according to the solution technique used 2. Basic Principles and Calculations Solution of simple problems involving linear and nonlinear algebraic equations, ordinary differential equations and multiple linear and polynomial regressions using POLYMATH 3. Regression and Correlation of Data Correlation of various properties with strong emphasis on validation and comparison of different regression models

Contents of the Computer-Based Problem Solving Course 4. Problem Solving with Excel Exporting the POLYMATH model to Excel. Exploiting Excels capabilities for parametric runs, tabular and graphical presentation of the results and well organized documentation of the model, the data and the results 5. Problem Solving with MATLAB Exporting the POLYMATH model to MATLAB. Programming in MATLAB to enable carrying out parametric runs, storage of the results in appropriate arrays and tabular and graphical presentation of the results.

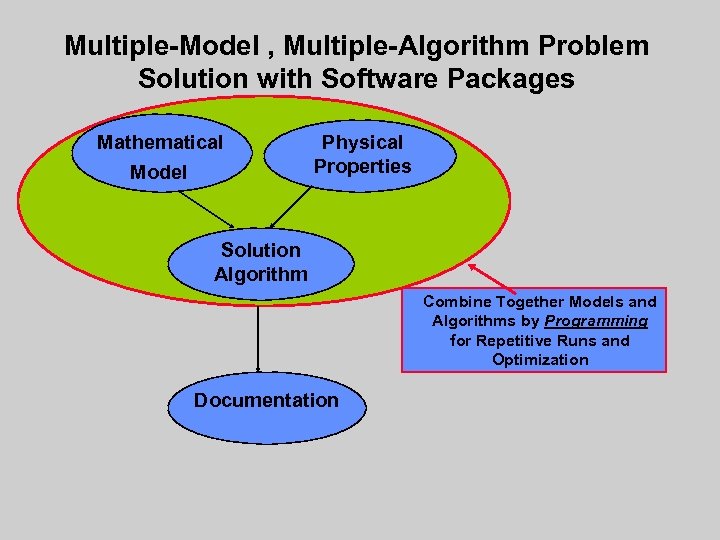
Multiple-Model , Multiple-Algorithm Problem Solution with Software Packages Mathematical Model Physical Properties Solution Algorithm Combine Together Models and Algorithms by Programming for Repetitive Runs and Optimization Documentation

Three Modes in the Operation of the Semi-batch Bioreactor S (substrate, reactant) + X (cell) = P (product) + n. X

Three Modes in the Operation of the Semi-batch Bioreactor Substrate feed rate FI Substrate feed rate FP Discharge flow rate FH Final volume VI Final Volume VH Final Volume VI S (substrate, reactant) + X (cell) = P (product) + n. X The biochemical reaction is inhibited by the substrate Optimal substrate feed concentration is required with fixed set of operating conditions n – cycle number n = 1 fedbatch operation

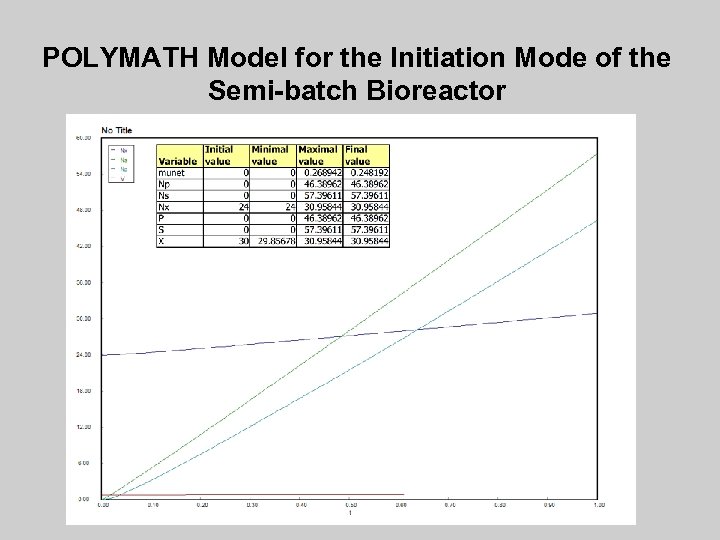
POLYMATH Model for the Initiation Mode of the Semi-batch Bioreactor

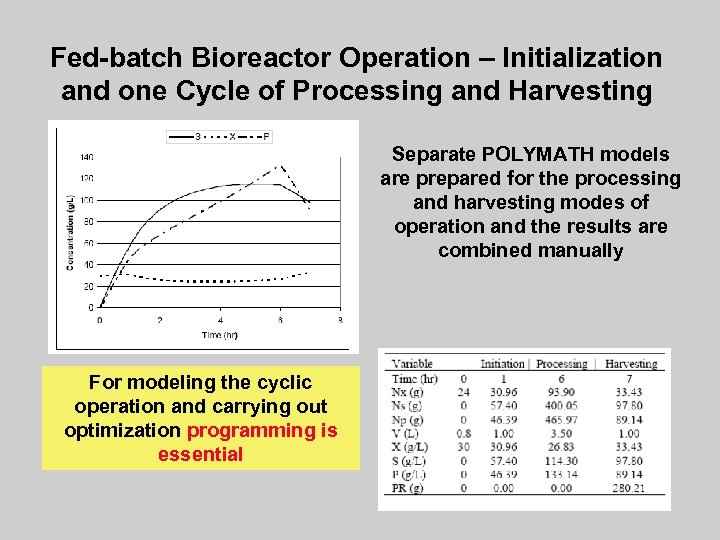
Fed-batch Bioreactor Operation – Initialization and one Cycle of Processing and Harvesting Separate POLYMATH models are prepared for the processing and harvesting modes of operation and the results are combined manually For modeling the cyclic operation and carrying out optimization programming is essential

POLYMATH generated MATLAB Function for the Initiation Mode Operation of the Bioreactor Conversion of vector contents to variable names Collection of the variables into a column vector

Part of the MATLAB “Main Program” for Simulation of Ten Process Cycles Initialization Processing Harvesting

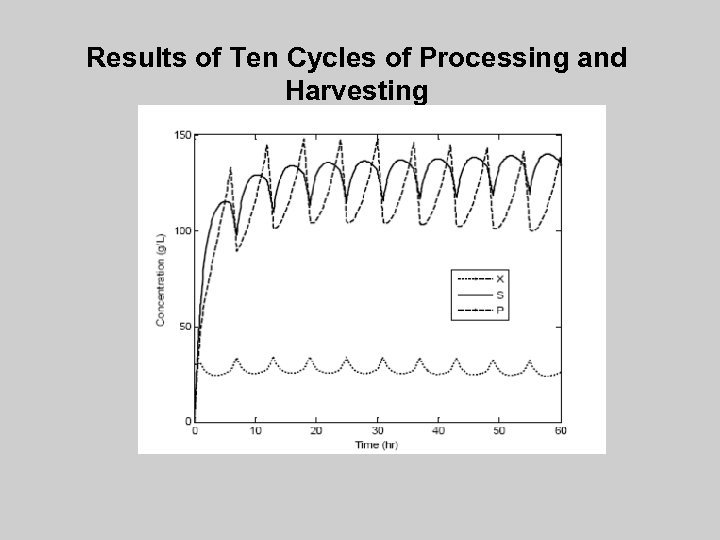
Results of Ten Cycles of Processing and Harvesting

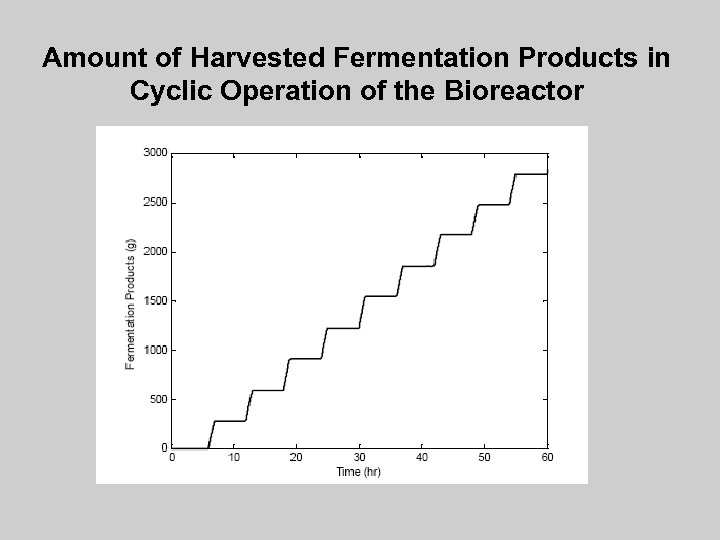
Amount of Harvested Fermentation Products in Cyclic Operation of the Bioreactor

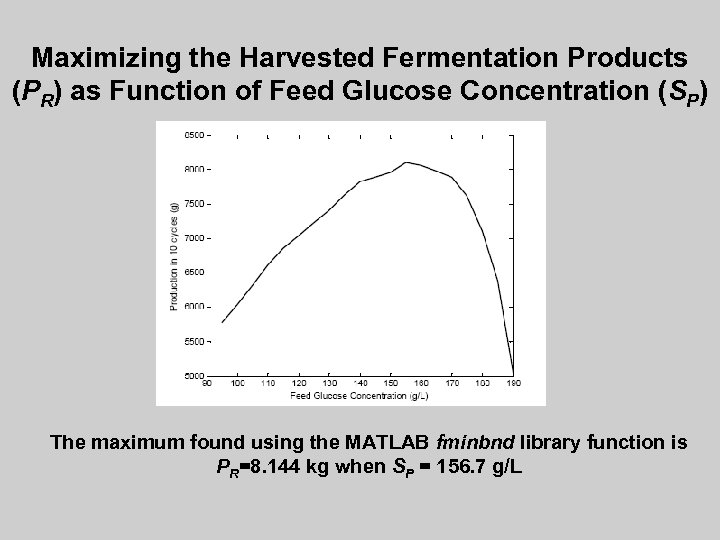
Maximizing the Harvested Fermentation Products (PR) as Function of Feed Glucose Concentration (SP) The maximum found using the MATLAB fminbnd library function is PR=8. 144 kg when SP = 156. 7 g/L

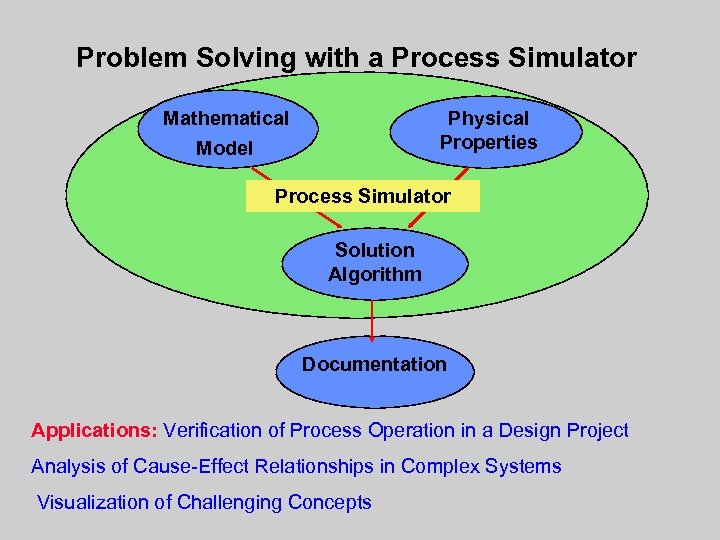
Problem Solving with a Process Simulator Mathematical Physical Properties Model Process Simulator Solution Algorithm Documentation Applications: Verification of Process Operation in a Design Project Analysis of Cause-Effect Relationships in Complex Systems Visualization of Challenging Concepts

CONCLUSIONS Ø Software tools of various levels of complexity and sophistication enable dividing the problem solving tasks between the user and the software package so that the goals of the problem solving can be most efficiently achieved Ø Using the programs effectively enables gaining good working ability with the basic tools (such as POLYMATH, Excel and MATLAB) and familiarity on some level with the more complex tools of process simulation, CFD and molecular simulation programs, within the framework of the undergraduate curriculum

Software References • Excel is a product of Microsoft Corporation http: //www. microsoft. com/ • MATLAB is a product of Mathworks http: //www. mathworks. com • Polymath is a product of Polymath Software http: // www. polymath-software. com/