cc1cc1ef31cc568e1bce14fd0b10b521.ppt
- Количество слайдов: 43
 From Linear Systems to Discrete-Event Systems W. M. Wonham Systems Control Group ECE Department University of Toronto Update 2006. 07. 01
From Linear Systems to Discrete-Event Systems W. M. Wonham Systems Control Group ECE Department University of Toronto Update 2006. 07. 01
 What is a Discrete-Event System? • Structure with ‘states’ having duration in time, ‘events’ happening instantaneously and asynchronously. • States: e. g. a machine is idle, is operating, is broken down, is under repair. • Events: machine starts work, breaks down, completes work or repair. • State space discrete in time and space. • State transitions ‘labeled’ by events.
What is a Discrete-Event System? • Structure with ‘states’ having duration in time, ‘events’ happening instantaneously and asynchronously. • States: e. g. a machine is idle, is operating, is broken down, is under repair. • Events: machine starts work, breaks down, completes work or repair. • State space discrete in time and space. • State transitions ‘labeled’ by events.
 Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
 Systems Control Concepts (c. 1980) • State space framework well-established: Controllability Observability Optimality (Quadratic, Lvarious, H ) • Qualitative synthesis via controlled dynamic invariants • Use of geometric constructs and partial order: Controllability subspaces (c. s. ) - supremal subspaces!
Systems Control Concepts (c. 1980) • State space framework well-established: Controllability Observability Optimality (Quadratic, Lvarious, H ) • Qualitative synthesis via controlled dynamic invariants • Use of geometric constructs and partial order: Controllability subspaces (c. s. ) - supremal subspaces!
 Discrete-Event Systems (c. 1980) • Practical problems • Programming languages for modeling & simulation • Queues, Markov chains • Petri nets • Boolean models • Formal languages • Process algebra (CSP, CCS)
Discrete-Event Systems (c. 1980) • Practical problems • Programming languages for modeling & simulation • Queues, Markov chains • Petri nets • Boolean models • Formal languages • Process algebra (CSP, CCS)
 Discrete-Event Systems Control (c. 1980) • Control problems implicit in the literature (enforcement of resource constraints, synchronization, . . . ) But • Emphasis on modeling, simulation, verification • Little formalization of control synthesis • Absence of control-theoretic ideas • No standard model or approach to control
Discrete-Event Systems Control (c. 1980) • Control problems implicit in the literature (enforcement of resource constraints, synchronization, . . . ) But • Emphasis on modeling, simulation, verification • Little formalization of control synthesis • Absence of control-theoretic ideas • No standard model or approach to control
 Needed (1980): DES Control Theory • System model Discrete in time and (usually) space Asynchronous (event-driven) Nondeterministic - support transitional choices • Amenable to formal control synthesis - exploit control concepts • Applicable: manufacturing, traffic, logistic, . . .
Needed (1980): DES Control Theory • System model Discrete in time and (usually) space Asynchronous (event-driven) Nondeterministic - support transitional choices • Amenable to formal control synthesis - exploit control concepts • Applicable: manufacturing, traffic, logistic, . . .
 Proposed (1982): Supervisory Control Theory (Ramadge & Wonham) • Automaton representation - internal state descriptions for concrete modeling and computation • Language representation - external i/o descriptions for implementation-independent concept formulation • Simple control ‘technology’
Proposed (1982): Supervisory Control Theory (Ramadge & Wonham) • Automaton representation - internal state descriptions for concrete modeling and computation • Language representation - external i/o descriptions for implementation-independent concept formulation • Simple control ‘technology’
![Community Response Anonymous Referees (1983 -86) • [Automatic control journal] “Automata have no place Community Response Anonymous Referees (1983 -86) • [Automatic control journal] “Automata have no place](https://present5.com/presentation/cc1cc1ef31cc568e1bce14fd0b10b521/image-9.jpg) Community Response Anonymous Referees (1983 -86) • [Automatic control journal] “Automata have no place in control engineering. ” Reject! • [Mathematical systems journal] “Finite automata and regular languages are nothing new at best and trivial at worst. ” Reject! • SIAM J. Control & Optimization “So this is optimal control? Well. . . ” Accept
Community Response Anonymous Referees (1983 -86) • [Automatic control journal] “Automata have no place in control engineering. ” Reject! • [Mathematical systems journal] “Finite automata and regular languages are nothing new at best and trivial at worst. ” Reject! • SIAM J. Control & Optimization “So this is optimal control? Well. . . ” Accept
 Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
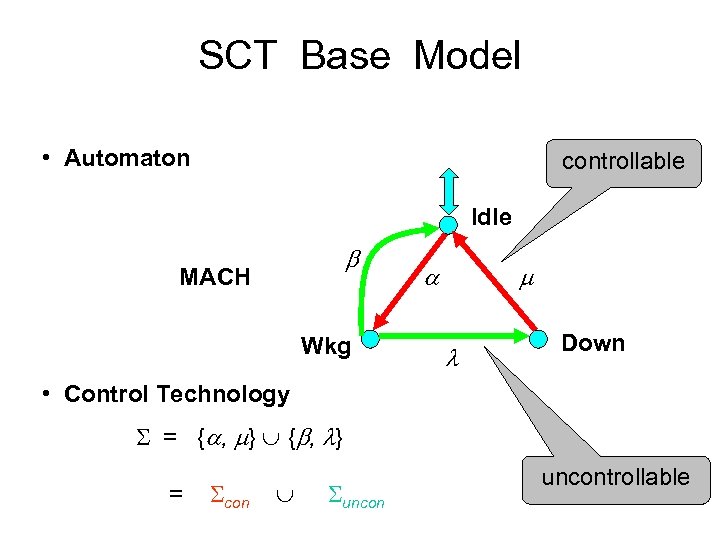 SCT Base Model • Automaton controllable Idle MACH Wkg Down • Control Technology = { , } = con uncontrollable
SCT Base Model • Automaton controllable Idle MACH Wkg Down • Control Technology = { , } = con uncontrollable
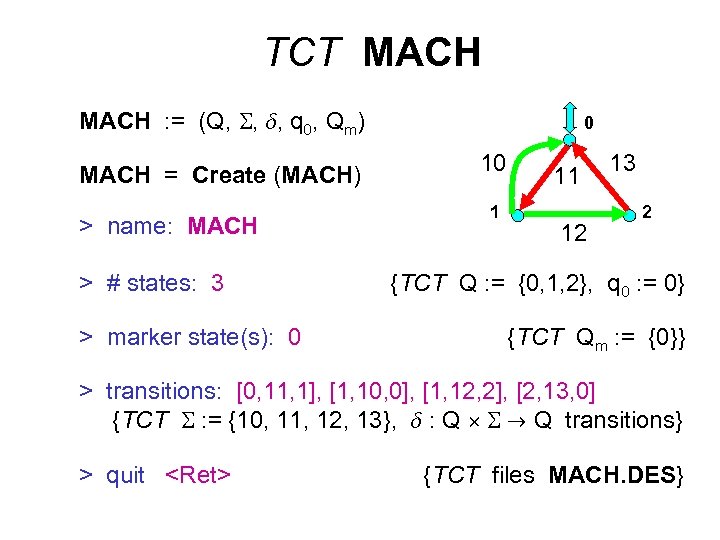 TCT MACH : = (Q, , , q 0, Qm) MACH = Create (MACH) > name: MACH > # states: 3 > marker state(s): 0 0 10 1 11 12 13 2 {TCT Q : = {0, 1, 2}, q 0 : = 0} {TCT Qm : = {0}} > transitions: [0, 11, 1], [1, 10, 0], [1, 12, 2], [2, 13, 0] {TCT : = {10, 11, 12, 13}, : Q Q transitions} > quit
TCT MACH : = (Q, , , q 0, Qm) MACH = Create (MACH) > name: MACH > # states: 3 > marker state(s): 0 0 10 1 11 12 13 2 {TCT Q : = {0, 1, 2}, q 0 : = 0} {TCT Qm : = {0}} > transitions: [0, 11, 1], [1, 10, 0], [1, 12, 2], [2, 13, 0] {TCT : = {10, 11, 12, 13}, : Q Q transitions} > quit
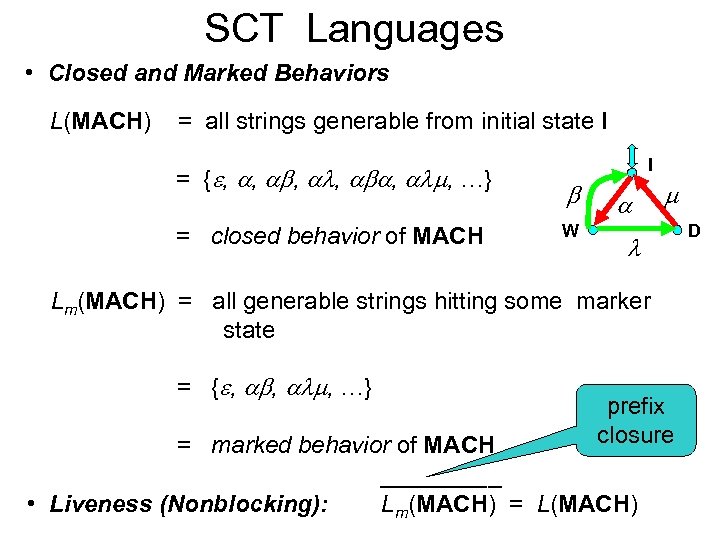 SCT Languages • Closed and Marked Behaviors L(MACH) = all strings generable from initial state I = { , , , , …} = closed behavior of MACH I W Lm(MACH) = all generable strings hitting some marker state = { , , , …} prefix closure = marked behavior of MACH _____ • Liveness (Nonblocking): Lm(MACH) = L(MACH) D
SCT Languages • Closed and Marked Behaviors L(MACH) = all strings generable from initial state I = { , , , , …} = closed behavior of MACH I W Lm(MACH) = all generable strings hitting some marker state = { , , , …} prefix closure = marked behavior of MACH _____ • Liveness (Nonblocking): Lm(MACH) = L(MACH) D
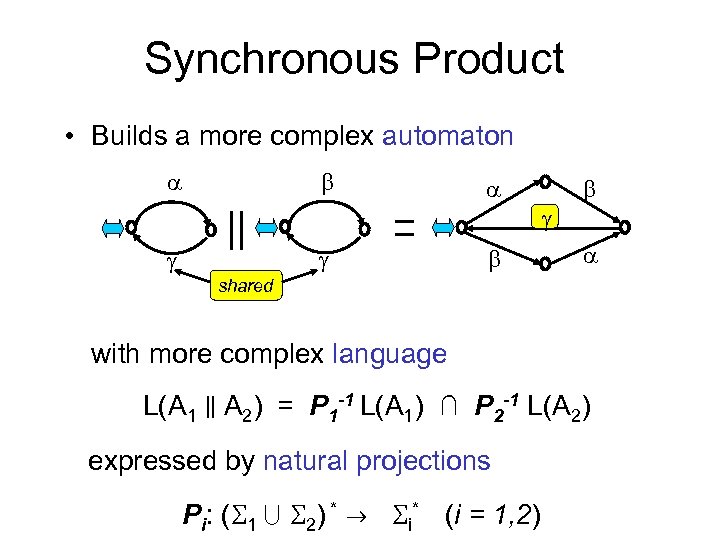 Synchronous Product • Builds a more complex automaton shared with more complex language L(A 1 A 2) = P 1 -1 L(A 1) P 2 -1 L(A 2) expressed by natural projections Pi: ( 1 2) * i* (i = 1, 2)
Synchronous Product • Builds a more complex automaton shared with more complex language L(A 1 A 2) = P 1 -1 L(A 1) P 2 -1 L(A 2) expressed by natural projections Pi: ( 1 2) * i* (i = 1, 2)
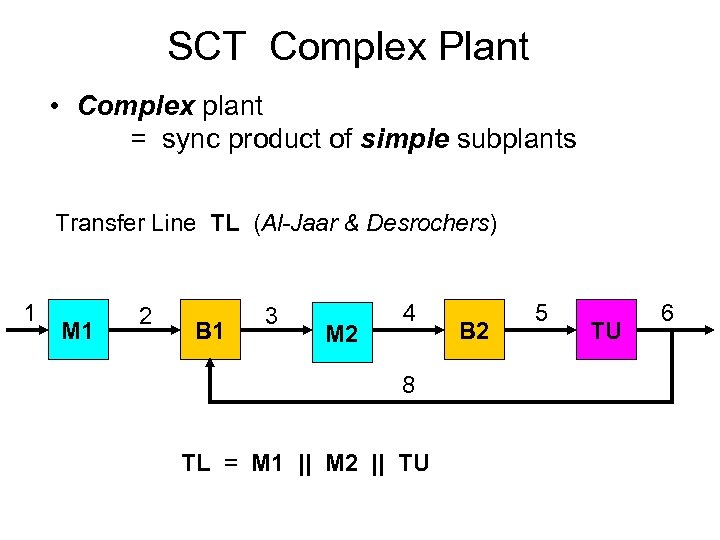 SCT Complex Plant • Complex plant = sync product of simple subplants Transfer Line TL (Al-Jaar & Desrochers) 1 M 1 2 B 1 3 M 2 4 8 TL = M 1 || M 2 || TU B 2 5 TU 6
SCT Complex Plant • Complex plant = sync product of simple subplants Transfer Line TL (Al-Jaar & Desrochers) 1 M 1 2 B 1 3 M 2 4 8 TL = M 1 || M 2 || TU B 2 5 TU 6
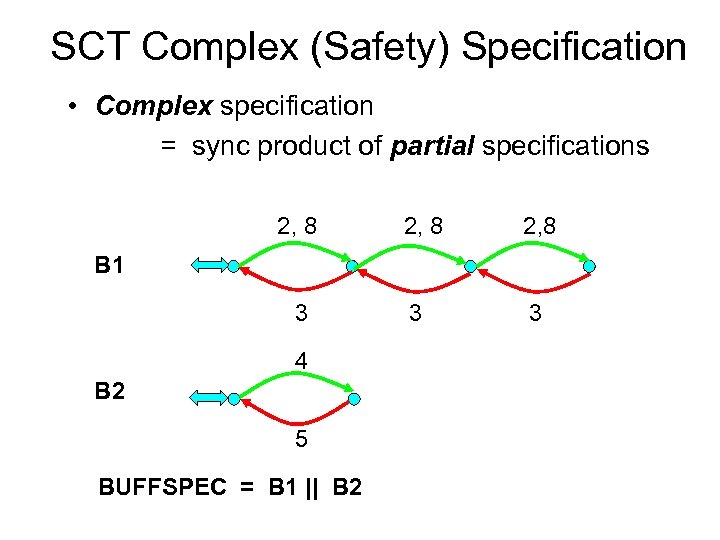 SCT Complex (Safety) Specification • Complex specification = sync product of partial specifications 2, 8 3 3 B 1 3 4 B 2 5 BUFFSPEC = B 1 || B 2
SCT Complex (Safety) Specification • Complex specification = sync product of partial specifications 2, 8 3 3 B 1 3 4 B 2 5 BUFFSPEC = B 1 || B 2
 General Control Issues • Is there a control that enforces both safety, and liveness (nonblocking), and which is maximally permissive ? • If so, can its design be automated ? • If so, with acceptable computing effort ?
General Control Issues • Is there a control that enforces both safety, and liveness (nonblocking), and which is maximally permissive ? • If so, can its design be automated ? • If so, with acceptable computing effort ?
 SCT Synthesis - Problem E. g. for TL, let Con. TL = ‘TL under control’ Must guarantee 1. Safety: Lm(Con. TL) Lm(BUFFSPEC) 2. Liveness (nonblocking): Lm(Con. TL) = L(Con. TL) 3. Maximal permissiveness: Lm(Con. TL) = maximum subject to safety and liveness
SCT Synthesis - Problem E. g. for TL, let Con. TL = ‘TL under control’ Must guarantee 1. Safety: Lm(Con. TL) Lm(BUFFSPEC) 2. Liveness (nonblocking): Lm(Con. TL) = L(Con. TL) 3. Maximal permissiveness: Lm(Con. TL) = maximum subject to safety and liveness
 SCT Synthesis - Solution E. g. for TL: 1. Fundamental definition A sublanguage K Lm(TL) is controllable if _ _ K uncon L(TL) K “Once in K, you can’t skid out on an uncontrollable event. ” 2. Fundamental result There exists a (unique) supremal controllable sublanguage Ksup Lm(TL) Lm(BUFFSPEC) Furthermore Ksup can be effectively computed.
SCT Synthesis - Solution E. g. for TL: 1. Fundamental definition A sublanguage K Lm(TL) is controllable if _ _ K uncon L(TL) K “Once in K, you can’t skid out on an uncontrollable event. ” 2. Fundamental result There exists a (unique) supremal controllable sublanguage Ksup Lm(TL) Lm(BUFFSPEC) Furthermore Ksup can be effectively computed.
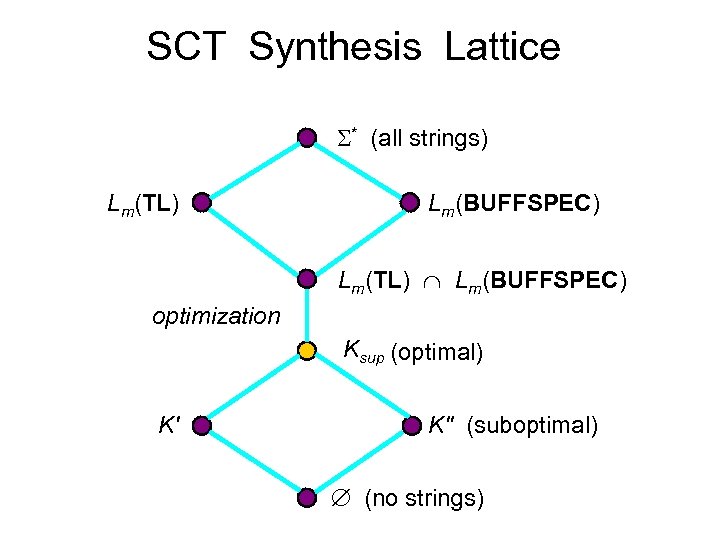 SCT Synthesis Lattice * (all strings) Lm(TL) Lm(BUFFSPEC) Lm(TL) Lm(BUFFSPEC) optimization Ksup (optimal) K' K" (suboptimal) (no strings)
SCT Synthesis Lattice * (all strings) Lm(TL) Lm(BUFFSPEC) Lm(TL) Lm(BUFFSPEC) optimization Ksup (optimal) K' K" (suboptimal) (no strings)
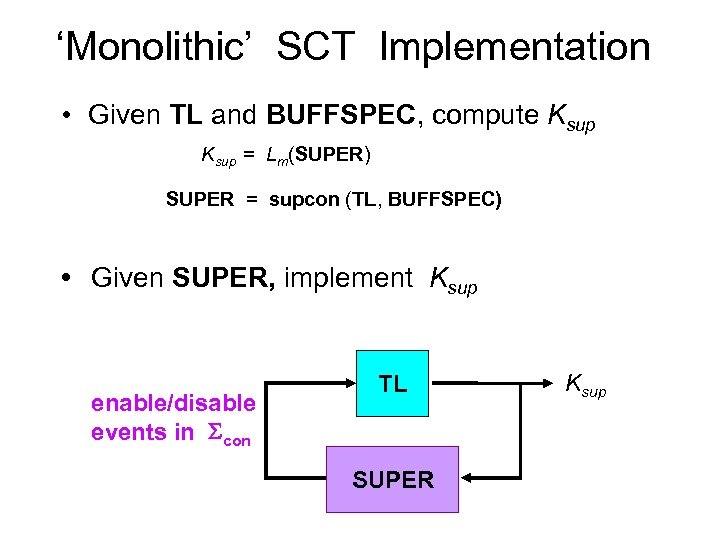 ‘Monolithic’ SCT Implementation • Given TL and BUFFSPEC, compute Ksup = Lm(SUPER) SUPER = supcon (TL, BUFFSPEC) • Given SUPER, implement Ksup enable/disable events in con TL SUPER Ksup
‘Monolithic’ SCT Implementation • Given TL and BUFFSPEC, compute Ksup = Lm(SUPER) SUPER = supcon (TL, BUFFSPEC) • Given SUPER, implement Ksup enable/disable events in con TL SUPER Ksup
 TCT TRANSFER LINE (TL) M 1 = Create (M 1), M 2 = Create (M 2), TU = Create (TU) TL = Sync (M 1, M 2, TU) B 1 = Create (B 1), {synchronous product} B 2 = Create (B 2) BUFFSPEC = Sync (B 1, B 2) {synchronous product} SUPER (. DES) = Sup. Con (TL, BUFFSPEC) {optimization} SUPER (. DAT) = Con. Dat (TL, SUPER(. DES)) {control data} SIMSUP = Sup. Reduce (TL, SUPER(. DES), SUPER(. DAT)) {supervisor reduction} SIMSUP (. DAT) = Con. Dat (TL, SIMSUP) {control data}
TCT TRANSFER LINE (TL) M 1 = Create (M 1), M 2 = Create (M 2), TU = Create (TU) TL = Sync (M 1, M 2, TU) B 1 = Create (B 1), {synchronous product} B 2 = Create (B 2) BUFFSPEC = Sync (B 1, B 2) {synchronous product} SUPER (. DES) = Sup. Con (TL, BUFFSPEC) {optimization} SUPER (. DAT) = Con. Dat (TL, SUPER(. DES)) {control data} SIMSUP = Sup. Reduce (TL, SUPER(. DES), SUPER(. DAT)) {supervisor reduction} SIMSUP (. DAT) = Con. Dat (TL, SIMSUP) {control data}
 Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
 Large DES PLANT = sync (PLANT. 1, … , PLANT. m) SPEC = sync (SPEC. 1, … , SPEC. n) SUPER = supcon (PLANT, SPEC) State size of SUPER ~ (Constant) m+n Exponential state space explosion ! ‘Extensional’ listing of ‘flat’ transition structures is impossible !
Large DES PLANT = sync (PLANT. 1, … , PLANT. m) SPEC = sync (SPEC. 1, … , SPEC. n) SUPER = supcon (PLANT, SPEC) State size of SUPER ~ (Constant) m+n Exponential state space explosion ! ‘Extensional’ listing of ‘flat’ transition structures is impossible !
 What To Do ? • In state representations, retain product structure PLANT state vector x = [x 1, . . . , xm] SPEC state vector y = [y 1, … , yn] • Express SUPER as a predicate Predsup (x, y, , x , y ) = 0 or 1 • Algorithmize representation of Predsup using Integer Decision Diagrams (IDDs)
What To Do ? • In state representations, retain product structure PLANT state vector x = [x 1, . . . , xm] SPEC state vector y = [y 1, … , yn] • Express SUPER as a predicate Predsup (x, y, , x , y ) = 0 or 1 • Algorithmize representation of Predsup using Integer Decision Diagrams (IDDs)
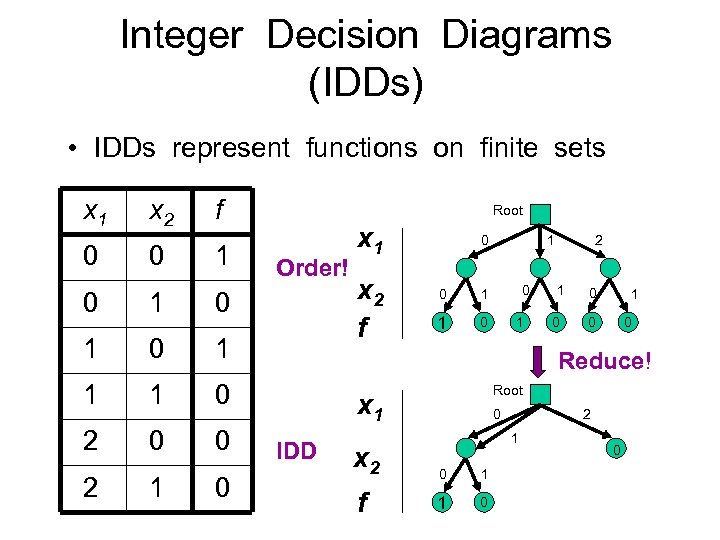 Integer Decision Diagrams (IDDs) • IDDs represent functions on finite sets x 1 0 x 2 0 f 1 0 1 1 1 0 2 0 0 Order! 0 1 Root 2 1 0 x 1 x 2 f 0 0 0 1 1 1 0 1 2 1 0 0 Reduce! Root x 1 IDD 0 2 1 x 2 0 1 f 1 0 0
Integer Decision Diagrams (IDDs) • IDDs represent functions on finite sets x 1 0 x 2 0 f 1 0 1 1 1 0 2 0 0 Order! 0 1 Root 2 1 0 x 1 x 2 f 0 0 0 1 1 1 0 1 2 1 0 0 Reduce! Root x 1 IDD 0 2 1 x 2 0 1 f 1 0 0
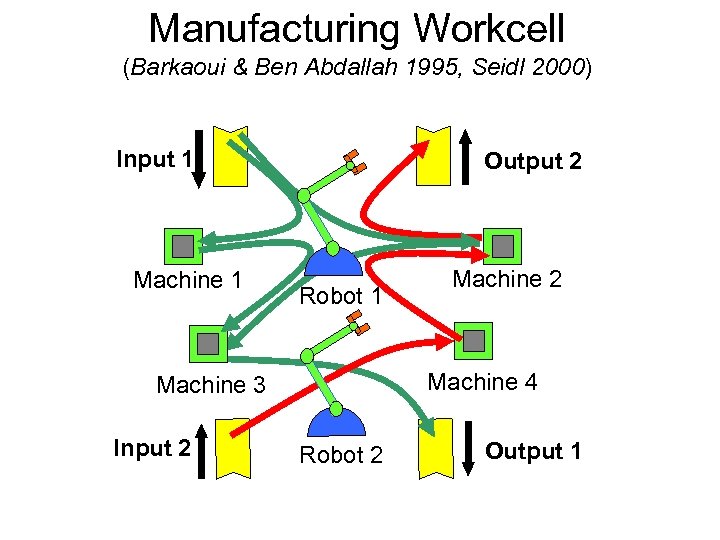 Manufacturing Workcell (Barkaoui & Ben Abdallah 1995, Seidl 2000) Input 1 Machine 1 Output 2 Robot 1 Machine 4 Machine 3 Input 2 Machine 2 Robot 2 Output 1
Manufacturing Workcell (Barkaoui & Ben Abdallah 1995, Seidl 2000) Input 1 Machine 1 Output 2 Robot 1 Machine 4 Machine 3 Input 2 Machine 2 Robot 2 Output 1
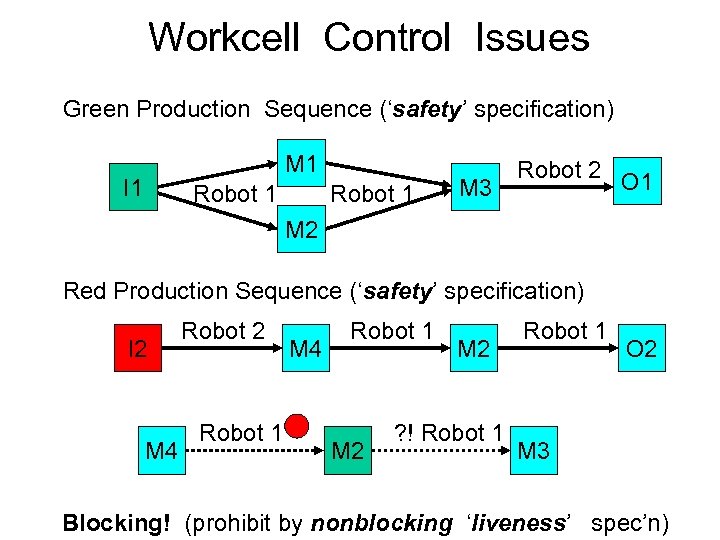 Workcell Control Issues Green Production Sequence (‘safety’ specification) M 1 I 1 Robot 1 M 3 Robot 2 O 1 M 2 Red Production Sequence (‘safety’ specification) I 2 M 4 Robot 2 Robot 1 M 4 Robot 1 M 2 ? ! Robot 1 O 2 M 3 Blocking! (prohibit by nonblocking ‘liveness’ spec’n)
Workcell Control Issues Green Production Sequence (‘safety’ specification) M 1 I 1 Robot 1 M 3 Robot 2 O 1 M 2 Red Production Sequence (‘safety’ specification) I 2 M 4 Robot 2 Robot 1 M 4 Robot 1 M 2 ? ! Robot 1 O 2 M 3 Blocking! (prohibit by nonblocking ‘liveness’ spec’n)
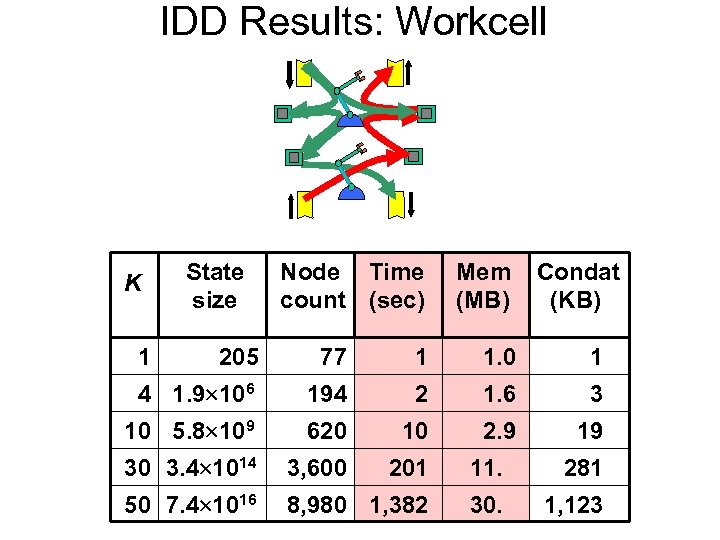 IDD Results: Workcell K State size Node Time count (sec) Mem (MB) Condat (KB) 205 77 1 1. 0 1 4 1. 9 106 194 2 1. 6 3 10 5. 8 109 620 10 2. 9 19 30 3. 4 1014 3, 600 201 11. 281 50 7. 4 1016 8, 980 1, 382 30. 1, 123 1
IDD Results: Workcell K State size Node Time count (sec) Mem (MB) Condat (KB) 205 77 1 1. 0 1 4 1. 9 106 194 2 1. 6 3 10 5. 8 109 620 10 2. 9 19 30 3. 4 1014 3, 600 201 11. 281 50 7. 4 1016 8, 980 1, 382 30. 1, 123 1
 Computing Effort vs. |Nodes| • Computing time ~ |Nodes|1. 5 << |States| • Memory usage ~ |Nodes| K • For ‘loosely coupled’ practical systems |Nodes| ~ N K C where N = number of system components (m+n) K state size of individual automata C = coupling coefficient 2 • |Nodes| linear (not exponential!) in N
Computing Effort vs. |Nodes| • Computing time ~ |Nodes|1. 5 << |States| • Memory usage ~ |Nodes| K • For ‘loosely coupled’ practical systems |Nodes| ~ N K C where N = number of system components (m+n) K state size of individual automata C = coupling coefficient 2 • |Nodes| linear (not exponential!) in N
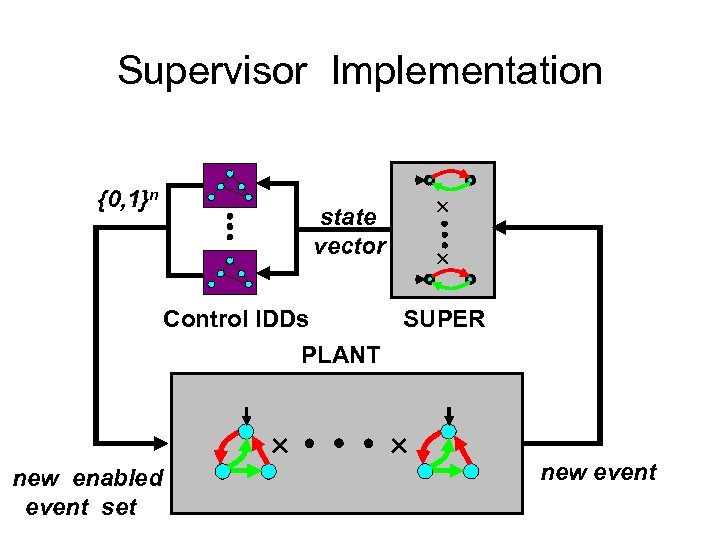 Supervisor Implementation {0, 1}n state vector Control IDDs SUPER PLANT new enabled event set new event
Supervisor Implementation {0, 1}n state vector Control IDDs SUPER PLANT new enabled event set new event
 Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
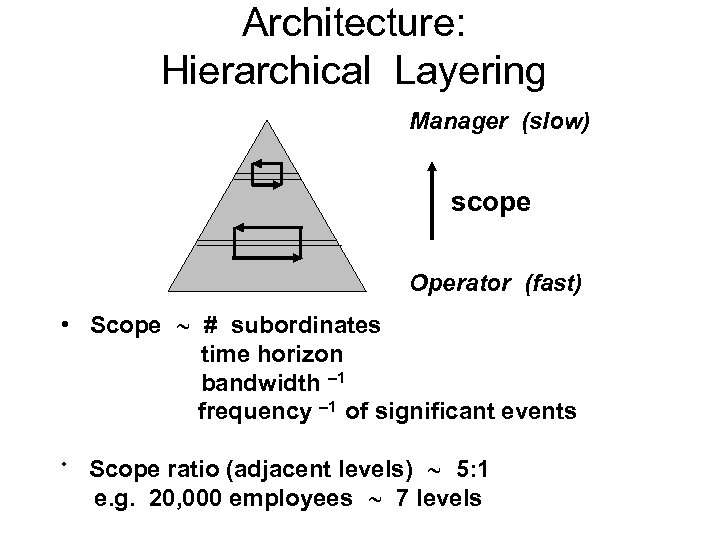 Architecture: Hierarchical Layering Manager (slow) scope Operator (fast) • Scope # subordinates time horizon bandwidth – 1 frequency – 1 of significant events • Scope ratio (adjacent levels) 5: 1 e. g. 20, 000 employees 7 levels
Architecture: Hierarchical Layering Manager (slow) scope Operator (fast) • Scope # subordinates time horizon bandwidth – 1 frequency – 1 of significant events • Scope ratio (adjacent levels) 5: 1 e. g. 20, 000 employees 7 levels
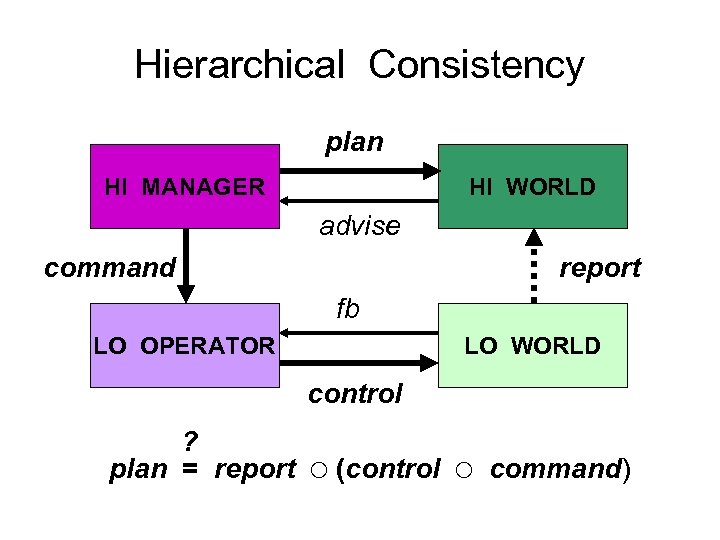 Hierarchical Consistency plan HI MANAGER HI WORLD advise command report fb LO OPERATOR LO WORLD control ? plan = report (control command)
Hierarchical Consistency plan HI MANAGER HI WORLD advise command report fb LO OPERATOR LO WORLD control ? plan = report (control command)
 Report and Command PLANThi T T* M report PLANTlo * L (M) command -1 (L) report is modelled by : L T *, (L) =: M command is modelled by -1 : (M) (L)
Report and Command PLANThi T T* M report PLANTlo * L (M) command -1 (L) report is modelled by : L T *, (L) =: M command is modelled by -1 : (M) (L)
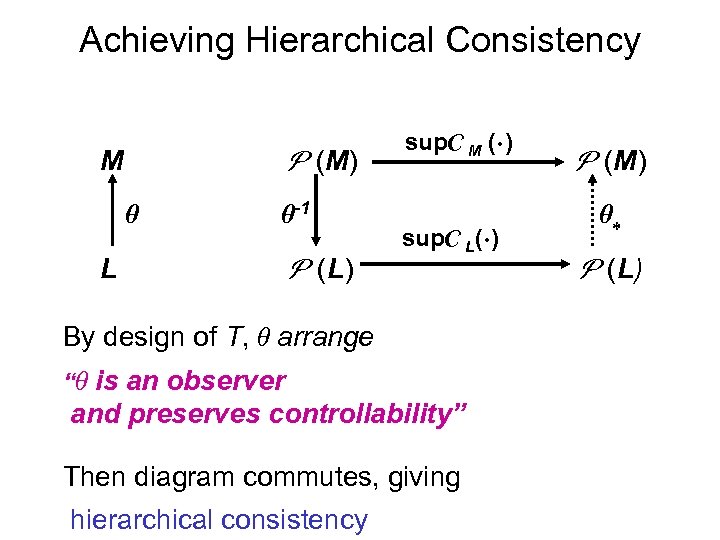 Achieving Hierarchical Consistency (M) M -1 L (L) sup M ( ) sup L( ) By design of T, arrange “ is an observer and preserves controllability” Then diagram commutes, giving hierarchical consistency (M) (L)
Achieving Hierarchical Consistency (M) M -1 L (L) sup M ( ) sup L( ) By design of T, arrange “ is an observer and preserves controllability” Then diagram commutes, giving hierarchical consistency (M) (L)
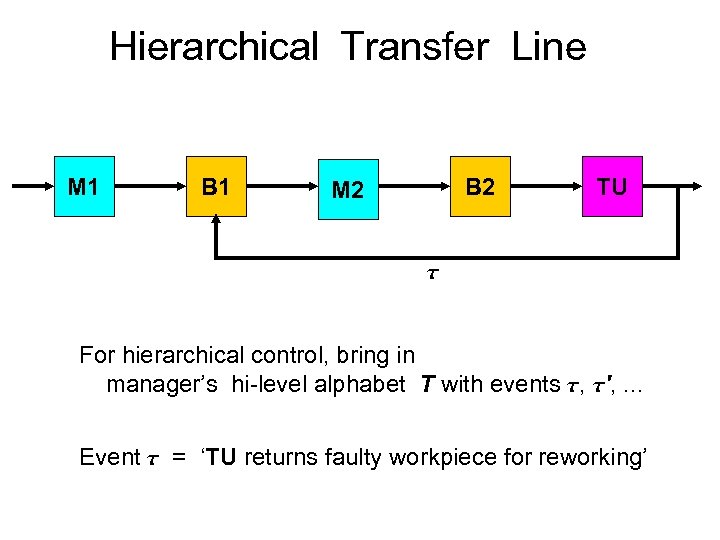 Hierarchical Transfer Line M 1 B 2 M 2 TU For hierarchical control, bring in manager’s hi-level alphabet T with events , ', . . . Event = ‘TU returns faulty workpiece for reworking’
Hierarchical Transfer Line M 1 B 2 M 2 TU For hierarchical control, bring in manager’s hi-level alphabet T with events , ', . . . Event = ‘TU returns faulty workpiece for reworking’
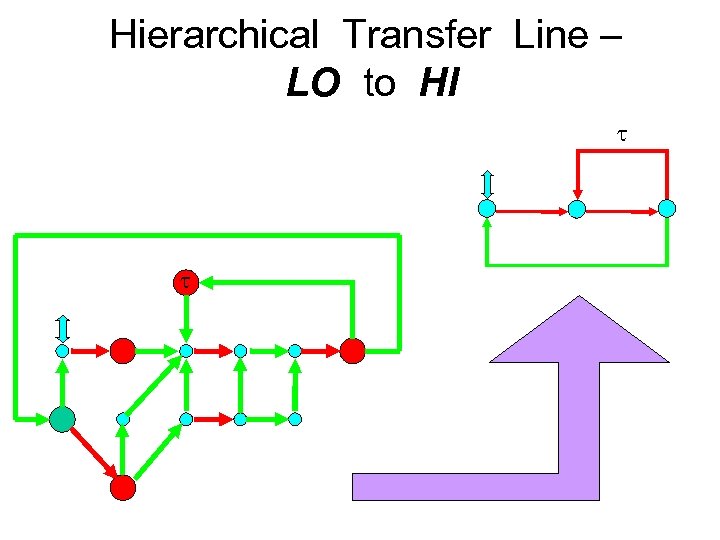 Hierarchical Transfer Line – LO to HI
Hierarchical Transfer Line – LO to HI
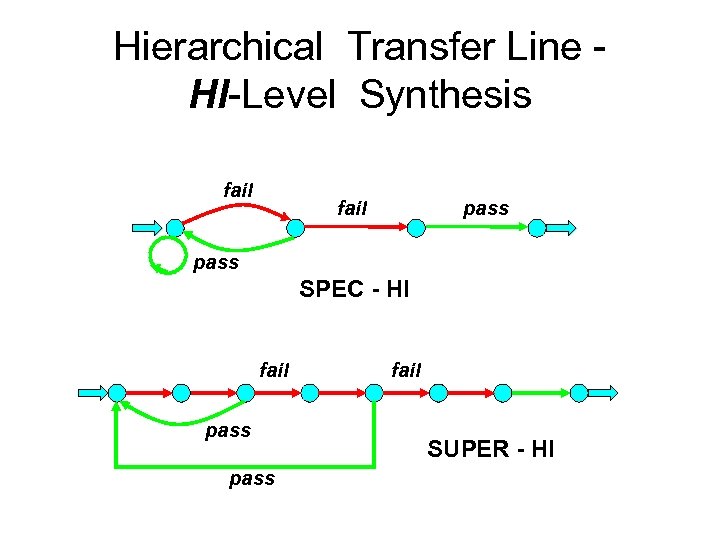 Hierarchical Transfer Line HI-Level Synthesis fail pass SPEC - HI fail pass fail SUPER - HI
Hierarchical Transfer Line HI-Level Synthesis fail pass SPEC - HI fail pass fail SUPER - HI
 Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
Summary • • • Some history Supervisory Control Theory (SCT) Large systems (using IDDs) Hierarchy Extensions and Applications Conclusions
 Extensions to Base Model • Forced (preemptive) events • Timed events (delays, deadlines, forcing) - Brandin, Saadatpoor • Liveness (= eventuality), temporal logic – infinite-string ( - languages) - Fusaoka, Thistle, Ramadge • Liveness (fairness, -calculus) - Thistle, Ziller • Algebraically hybrid (? ) – X = Q 1 . . . Qk n m
Extensions to Base Model • Forced (preemptive) events • Timed events (delays, deadlines, forcing) - Brandin, Saadatpoor • Liveness (= eventuality), temporal logic – infinite-string ( - languages) - Fusaoka, Thistle, Ramadge • Liveness (fairness, -calculus) - Thistle, Ziller • Algebraically hybrid (? ) – X = Q 1 . . . Qk n m
 Some Applications • Communication protocol specification (Rudie 1990) • Rapid thermal multiprocessor (Hoffmann 1991) • Robotic agents (Kosecka 1994) • AIP automated manufacturing system (Brandin 1994, Leduc 2001, Ma 2003) • Telephone feature interaction (Thistle 1995) • Chemical process control (Sanchez 1996, Alsop 1996) • Truck dispatching (Blouin 2001) • Telephone directory assistance call center (Seidl 2004)
Some Applications • Communication protocol specification (Rudie 1990) • Rapid thermal multiprocessor (Hoffmann 1991) • Robotic agents (Kosecka 1994) • AIP automated manufacturing system (Brandin 1994, Leduc 2001, Ma 2003) • Telephone feature interaction (Thistle 1995) • Chemical process control (Sanchez 1996, Alsop 1996) • Truck dispatching (Blouin 2001) • Telephone directory assistance call center (Seidl 2004)
 Conclusions • Achievements of SCT: * Synthetic and general * Results correct by construction and computable for large systems * Modular architecture for management of complexity * Easy to teach and use (e. g. materials on Internet) • Challenges for SCT: * How to interpret and modify controller structure (e. g. IDDs linear inequalities) ? * How to find general laws of architecture ?
Conclusions • Achievements of SCT: * Synthetic and general * Results correct by construction and computable for large systems * Modular architecture for management of complexity * Easy to teach and use (e. g. materials on Internet) • Challenges for SCT: * How to interpret and modify controller structure (e. g. IDDs linear inequalities) ? * How to find general laws of architecture ?


