b85266f1b01c890226a04efd24227aee.ppt
- Количество слайдов: 9

Free Riders and Distortionary Zoning by Local Communities Thomas J. Miceli Department of Economics @ The University of Connecticut Journal of Urban Economics 30, 112 -122 (1991) Jacquelyn R. Martin Economics 8500 – Fall 2002 – December 18 th Dr. Goodman, Professor

Introduction This paper is an analysis of the distortionary impacts of zoning policies that regulate housing consumption. It examines a community’s motivation for enacting zoning. -Basis Notions: * Newcomers to community will ‘free-ride’ in the consumption of public services by under-consuming housing that is less than the community average without zoning. -Two important reasons for imposing zoning is: (1) to increase the community’s tax base (2) to prevent free-riding

Suppose: - That a community was established by competitive, profit maximizing developers who ensured that resources were allocated efficiently within that community. ** That is…that the level of public services are Pareto-efficient. -Homogenous community consisting of N identical residents -Each with utility function V = V (x, h, g) x = a composite consumption good h = housing service g = level of public good …denoted h*, that satisfies the condition of Vh / Vx = p, where p is opportunity cost of a unit of housing …g @ constant cost c, makes g a private good So, that the community budget is shown by cg. N.

Miceli first considered the two types of tax assessment practices for property taxes: 1. Purchase Price Assessment 2. Uniform Assessment. Purchase Price Assessment Uniform Tax Assessment - Tax assessment based on the purchase price of the house, tph -Tax assessment based on the product assessment rate, a, (let a = 1) and the quantity of housing service, h; tah -In a homogenous community, tph*N -Solving for t t = cg / ph* Resident budget constraint is y = x + ph* (1 + t), where gph = p(1 + t) -In a homogenous community, th*N -Solving for t t = cg / h* Resident budget constraint is y = x + (p + t) h*, where p + t is gph
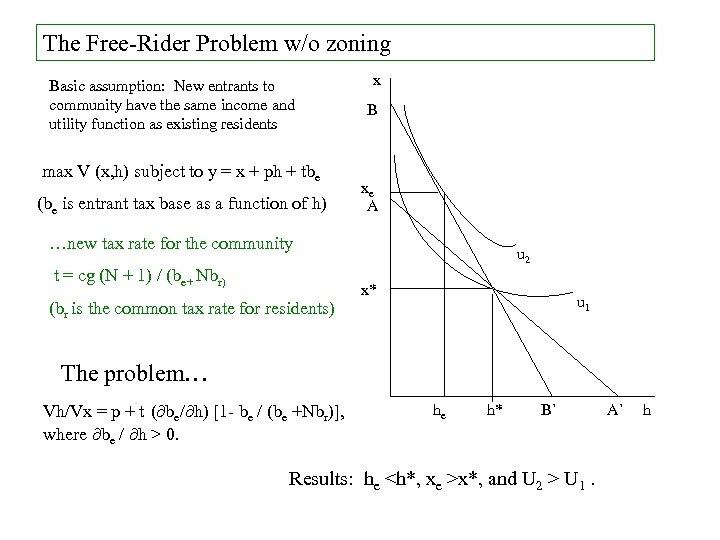
The Free-Rider Problem w/o zoning Basic assumption: New entrants to community have the same income and utility function as existing residents max V (x, h) subject to y = x + ph + tbe (be is entrant tax base as a function of h) x B xe A …new tax rate for the community t = cg (N + 1) / (be+ Nbr) (br is the common tax rate for residents) u 2 x* u 1 The problem… Vh/Vx = p + t ( be/ h) [1 - be / (be +Nbr)], where be / h > 0. he h* B` Results: he <h*, xe >x*, and U 2 > U 1. A` h
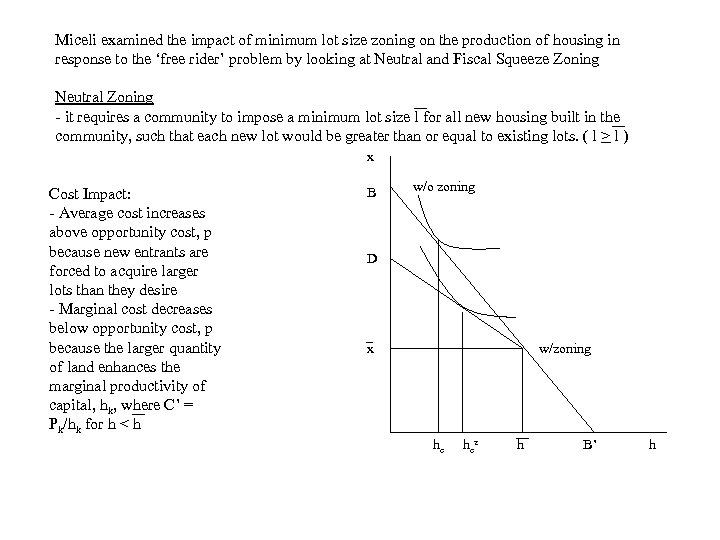
Miceli examined the impact of minimum lot size zoning on the production of housing in response to the ‘free rider’ problem by looking at Neutral and Fiscal Squeeze Zoning Neutral Zoning - it requires a community to impose a minimum lot size l for all new housing built in the community, such that each new lot would be greater than or equal to existing lots. ( l > l ) x Cost Impact: - Average cost increases above opportunity cost, p because new entrants are forced to acquire larger lots than they desire - Marginal cost decreases below opportunity cost, p because the larger quantity of land enhances the marginal productivity of capital, hk, where C’ = Pk/hk for h < h B w/o zoning D x w/zoning he hez h B’ h
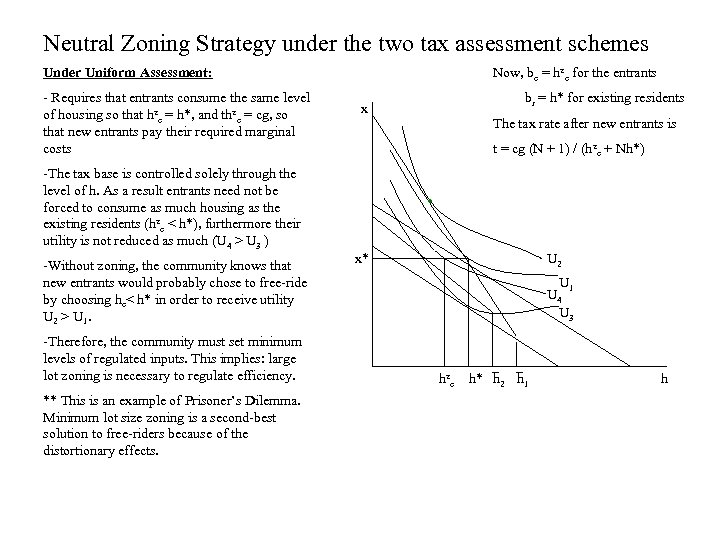
Neutral Zoning Strategy under the two tax assessment schemes Now, be = hze for the entrants Under Uniform Assessment: - Requires that entrants consume the same level of housing so that hze = h*, and thze = cg, so that new entrants pay their required marginal costs -Therefore, the community must set minimum levels of regulated inputs. This implies: large lot zoning is necessary to regulate efficiency. ** This is an example of Prisoner’s Dilemma. Minimum lot size zoning is a second-best solution to free-riders because of the distortionary effects. The tax rate after new entrants is t = cg (N + 1) / (hze + Nh*) -The tax base is controlled solely through the level of h. As a result entrants need not be forced to consume as much housing as the existing residents (hze < h*), furthermore their utility is not reduced as much (U 4 > U 3 ) -Without zoning, the community knows that new entrants would probably chose to free-ride by choosing he< h* in order to receive utility U 2 > U 1. br = h* for existing residents x • x* U 2 U 1 U 4 U 3 hze h* h 2 h 1 h
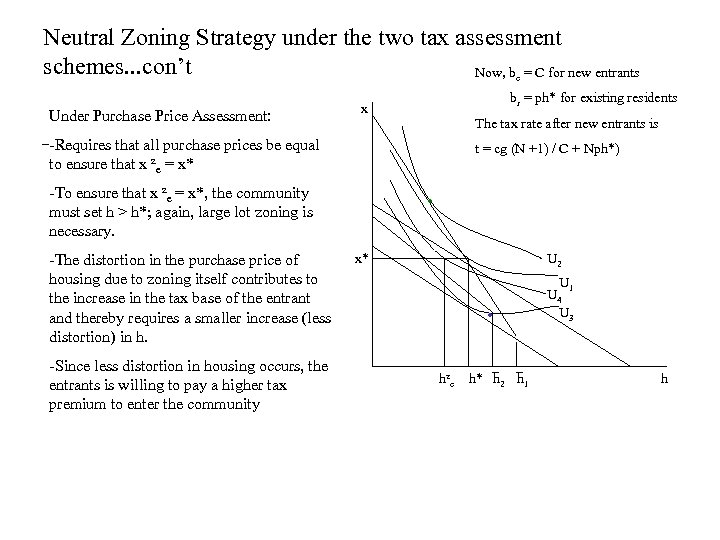
Neutral Zoning Strategy under the two tax assessment schemes. . . con’t Now, b = C for new entrants e Under Purchase Price Assessment: br = ph* for existing residents x The tax rate after new entrants is -Requires that all purchase prices be equal to ensure that x ze = x* t = cg (N +1) / C + Nph*) -To ensure that x ze = x*, the community must set h > h*; again, large lot zoning is necessary. -The distortion in the purchase price of housing due to zoning itself contributes to the increase in the tax base of the entrant and thereby requires a smaller increase (less distortion) in h. -Since less distortion in housing occurs, the entrants is willing to pay a higher tax premium to enter the community • x* U 2 • hze h* h 2 h 1 U 4 U 3 h

Conclusions PREVENTING FREE-RIDERS? Zoning is distortionary, so that even neutral zoning requires setting lot sizes larger than the average to prevent free-riders. * This was true in both the level of housing consumption or the purchase price of housing. However, the purchase price tax assessment strategy is much less distortionary than the uniform assessment strategy. RAISING TAX BASE? Using uniform assessment strategy, where be = h, minimum lot size zoning does not succeed in raising the tax base of newcomers, even when their alternatives are restricted. This does not hold true when using the purchase price assessment, since be = C is always increasing in l.
b85266f1b01c890226a04efd24227aee.ppt