Foundational Certified Code in a Metalogical Framework Karl

Foundational Certified Code in a Metalogical Framework Karl Crary and Susmit Sarkar Carnegie Mellon University

Motivation: Grid Computing Make use of idle computing cycles over the network [e. g. SETI] n Computer owners download and execute code from developers n A key issue: Unknown developers, so consumers are concerned about safety n 2

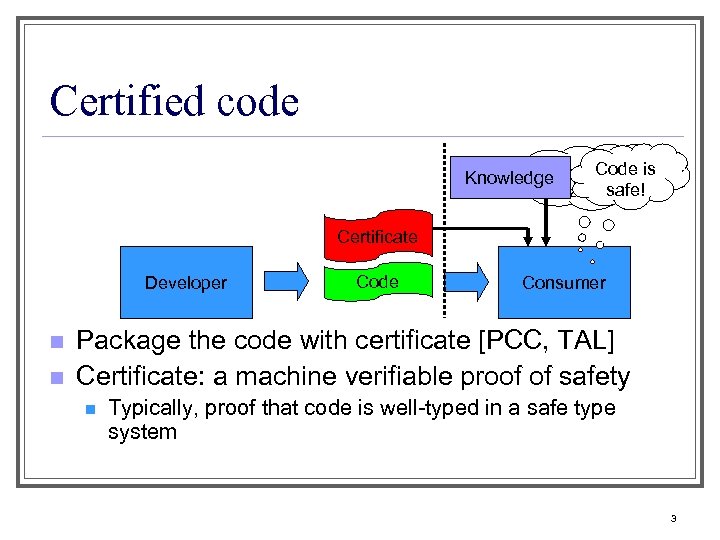Certified code Code is Knowledge Is code safe ? safe! Certificate Developer n n Code Consumer Package the code with certificate [PCC, TAL] Certificate: a machine verifiable proof of safety n Typically, proof that code is well-typed in a safe type system 3

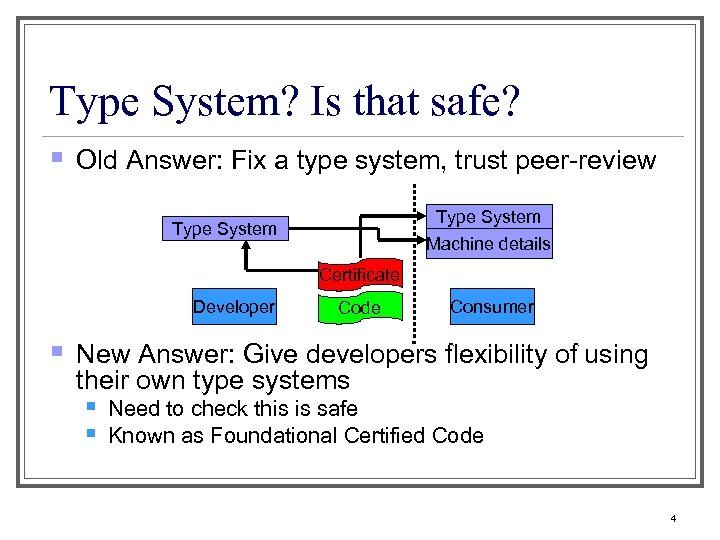Type System? Is that safe? § Old Answer: Fix a type system, trust peer-review Type System Machine details Certificate Developer § Code Consumer New Answer: Give developers flexibility of using their own type systems § Need to check this is safe § Known as Foundational Certified Code 4

Roadmap § Our system § Metalogics § Safety Policy § A Safety Proof § Related and future work 5

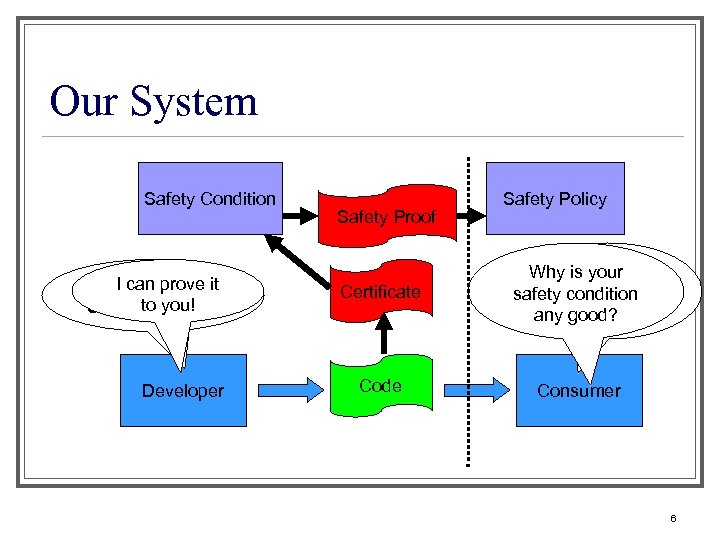Our System Safety Condition I satisfies my Code can prove it Safety to you! Condition Developer Safety Proof Certificate Code Safety Policy Why. Does Code is your safety condition satisfy the any good? Safety Policy? Consumer 6

Metalogic : meta theorems n We use LF to express logics n n n e. g. , operational semantics producer’s safety conditions We care about meta theorems: n n If some input derivation exists, then an output derivation exists e. g. , Safety Theorem 7

How to check meta theorems? Choice 1: reflect metalogical reasoning in the framework n Choice 2: use a logic designed for metalogical reasoning n n e. g. Twelf [Schurmann] 8

Programming in Meta logics n We write logic programs relating derivations n limited to -1 reasoning, authors plan stronger system Need to do induction on structure of derivation n System can check these logic programs are total (user annotations required) n 9

Roadmap Our system n Metalogics n Safety policy n A safety proof n Related and future work n 10

Safety policy - Preliminaries Formalize operational semantics of the IA 32 architecture n Formalize machine states: memory, register files, stack, instruction pointer n Formalize transitions from state to state n Remove transitions deemed unsafe n 11

Example: transition for addition n addl $5, (%eax) n n n n load 4 bytes from (%eax), load immediate operand 5, add them, store result back in (%eax), update EFLAGS and advance EIP This can go wrong, e. g. if eax points to protected memory Solution: The formal load and store relations do not apply in such cases 12

Safety Policy Define initial state on loading program P n We never get to a state where the (formal) machine does not have a transition n Another way of stating: the formal machine is never stuck n n Halt state treated specially 13

Why is this safe? Real machine’s transitions according to formal machine’s transitions: real machine is performing safe operations n To perform unsafe operations, real machine takes a transition not in formal machine n This does not happen in a safe machine n 14

Roadmap Our system n Metalogics n Safety policy n A safety proof n Related and future work n 15

Example Safety Proof n n A particular safety proof Our safety proof is for TALT [Crary] n n n Type system for an assembly language Fairly low-level, but still abstract Our foundational safety proof is syntactic [Hamid et al. ] 16

Safety n Our conditions will isolate a set of safe states n Safe states cannot transition to stuck states Safe State M 1 State M 2 17

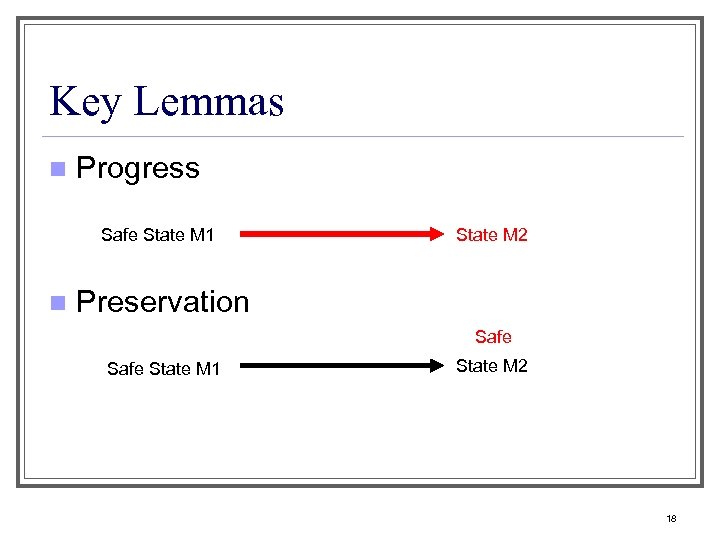Key Lemmas n Progress Safe State M 1 n State M 2 Preservation Safe State M 1 State M 2 18

Putting it together – Safety Theorem n Transitions from a safe state cannot go to a stuck state Safe State M 1 State M 2 19

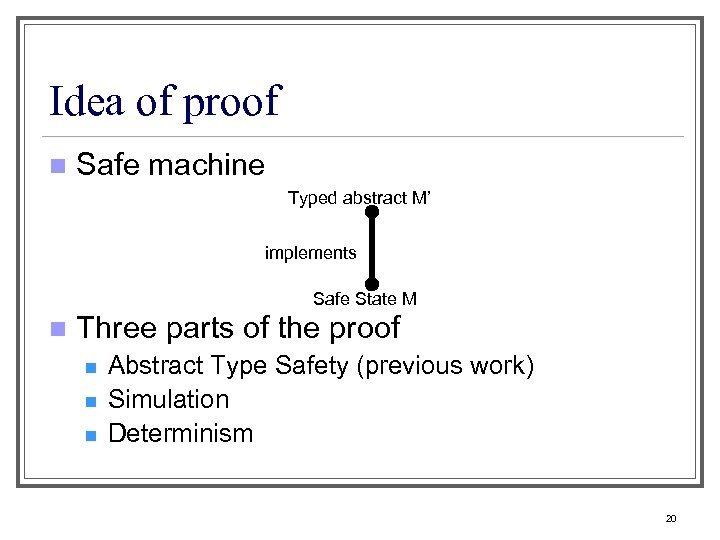Idea of proof n Safe machine Typed abstract M’ implements Safe State M n Three parts of the proof n n n Abstract Type Safety (previous work) Simulation Determinism 20

TALT safety proof [Crary] This has two top level lemmas: n Progress: A well typed abstract machine makes a transition n Preservation: If a well typed abstract machine makes a transition, the resulting (abstract) machine is well typed n 21

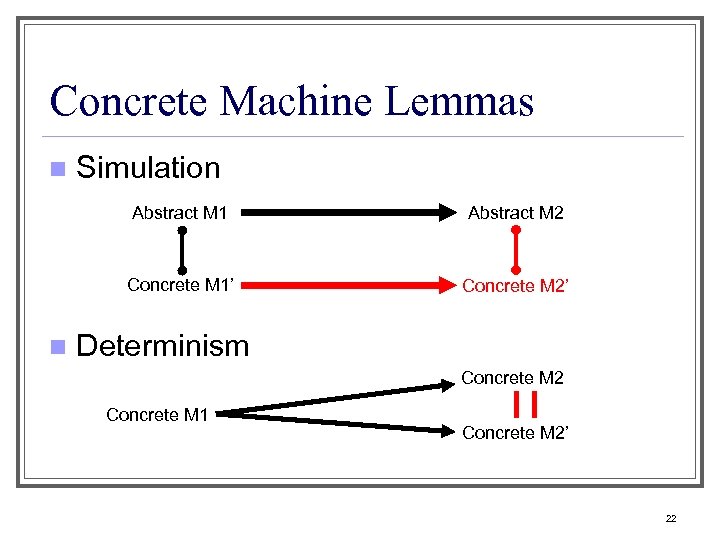Concrete Machine Lemmas n Simulation Abstract M 1 Concrete M 1’ n Abstract M 2 Concrete M 2’ Determinism Concrete M 2 Concrete M 1 Concrete M 2’ 22

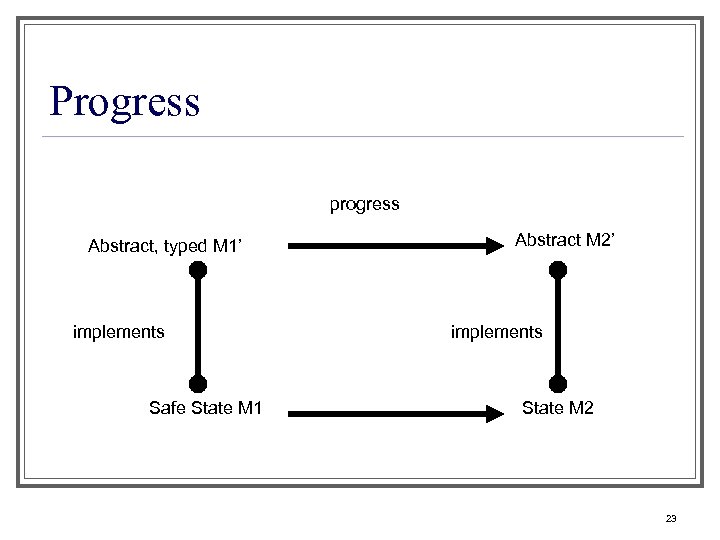Progress progress Abstract, typed M 1’ implements Safe State M 1 Abstract M 2’ implements State M 2 23

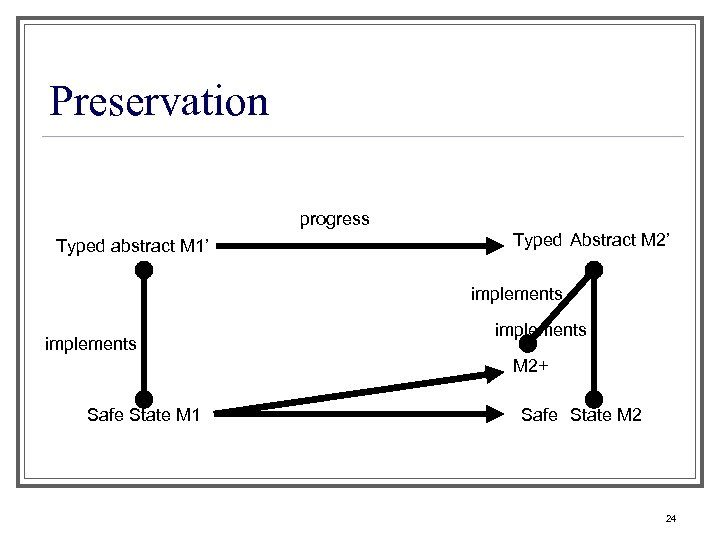Preservation progress Typed abstract M 1’ Typed Abstract M 2’ implements M 2+ Safe State M 1 Safe State M 2 24

Implementation Statistics Safety Policy : 2, 081 lines of code n Safety Proof : 44, 827 lines of code n Time to check : 75 sec n Number of lemmas : 1, 466 n Man years : 1 and 1/2 n 25

Related work Foundational PCC - Appel et al n FTAL - Hamid et al n Temporal Logic PCC - Bernard and Lee n 26

Future Work Develop a compiler from Standard ML to TALT n Expand the target language to include many more IA 32 instructions n Specify and prove other properties, e. g. Running time bounds n 27

28

Indeterminism The data may be indeterminate, due to e. g. input n Safety demands that any instance be safe n We have an oracle that the semantics consults to determine what to do n Oracle is quantified in safety theorem n 29