Фотохимия Надточенко Виктор Андреевич 79152269347 nadtochenko gmail com

Фотохимия Надточенко Виктор Андреевич +79152269347 nadtochenko@gmail. com

Фотохимическая реакция • Химическая реакция при условии возбуждения квантом света реагента.

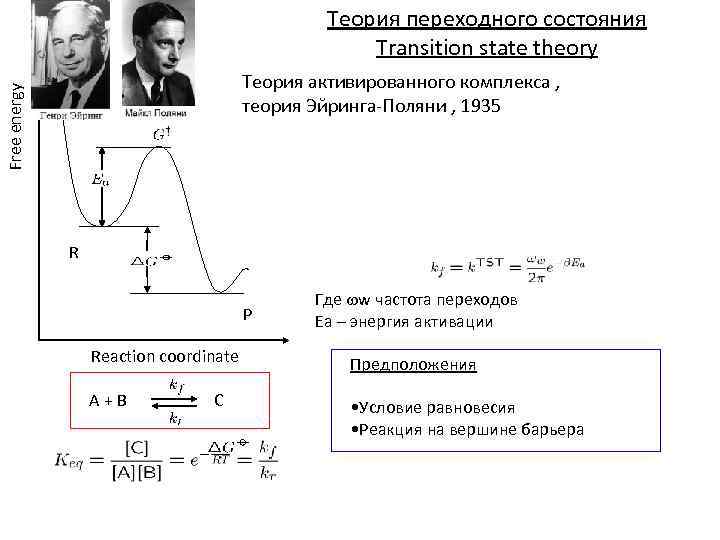Теория переходного состояния Transition state theory Free energy Теория активированного комплекса , теория Эйринга-Поляни , 1935 R P Где w частота переходов Еа – энергия активации Reaction coordinate Предположения A + B • Условие равновесия • Реакция на вершине барьера C

Пусть δ – область состояний вблизи вершины потенциального барьера. Большинство экспериментальных реакций преодолевают эту область протяженностью δ за конечный интервал времени τ.

В неадибатических процессах и реакциях с образованием одною частицей при малых давлениях учитывается вероятность достижения переходного состояния. С этой целью вводится коэффициент прохождения или трансмиссионный коэффициент χ и основная формула метода активированного комплекса записывается:

Reaction rates and Marcus theory (2) Теория Крамерса В теории Крамерса сохраняется предположение о равновесии H. A. Kramers (1894 -1952) b частота m – масса реакционной частицы - трение The Kramers rate is always lower than the rate В теории Крамерса скорость всегда ниже скорости calculated with TST. The reason is that now it рассчитанной по TST. Требуется не только достичь is not sufficient for the particle to reach the top вершины но и иметь достаточно скорости, чтобы of the barrier, it has to have sufficient velocity преодолеть её to go over it, or it will be sent back to the reactant well. Reaction coordinate http: //www. chem. msu. su/rus/teaching/vorob'ev/3. html

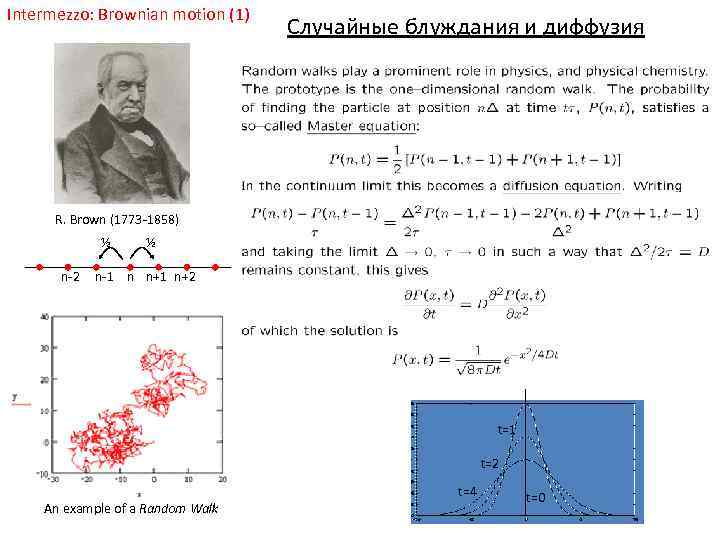Intermezzo: Brownian motion (1) Случайные блуждания и диффузия R. Brown (1773 -1858) ½ n-2 ½ n-1 n n+1 n+2 t=1 t=2 An example of a Random Walk t=4 t=0

Intermezzo: Brownian motion (2) P. Langevin (1872 -1946) v A particle drawn through a fluid experiences drag Уравнение Ланжевена

Теория Крамерса Другой метод явного учета процесса обмена энергией между реакционным комплексом и средой используется в модели Крамерса. Представим себе реакцию достаточно крупной молекулы в вязкой жидкости. Движение по координате реакции фрагментов молекулы со значительными массами не может быть очень быстрым. Молекулы растворителя, окружающие реакционный комплекс, находятся все время в контакте с ним и, таким образом, время релаксации, т. е. время обмена энергией со средой, мало. Реакционная система в жидкости характеризуется еще большим числом степеней свободы, чем реакционная система в газе. К внутренним степеням свободы молекулы необходимо прибавить степени свободы, характеризующие положение, ориентацию и колебания молекул среды, находящихся в контакте с реакционным комплексом. Выделим тем не менее степень свободы, отвечающую координате реакции. Остальные степени свободы будем рассматривать как тепловой резервуар, который находится в равновесии с реакционной степенью свободы. Появление на реакционной степени свободы необходимой энергии будем рассматривать как возникновение флуктуации. Крамерс предложил применить к движению изображающей точки по координате реакции формализм, предложенный для описания броуновской диффузии частицы в вязкой среде. Этот процесс описывается уравнением Ланжевена:

Если левую часть этого уравнения приравнять нулю, полученное выражение будет описывать затухающее движение в вязкой среде. Например, если потенциал параболический (для маятника, погруженного в жидкость), то движение будет периодическим затухающим колебанием. При любых начальных условиях такое движение очень быстро прекращается и достигается стационарное состояние системы. Ясно, что этот случай не может описать броуновскую диффузию, т. е. стохастический флуктуационный процесс, который никогда не останавливается. В связи с этим, в уравнение введена случайная сила f(t). Величина силы различна в различные моменты времени. Такая функция задается следующим образом: =0 = ( 1) = ( 1, 2) Случайная сила =k. T. -1. ( 1)

Константа скорости через с≠ . . Большое трение >>2 m .

Большое трение >> 2 m ≠ мало В случае большого трения коэффициент трения в уравнении Ланжевена достаточно велик, для установления максвеллбольцмановского равновесия. Тогда величина будет та же, что в теории переходного состояния c≠

Среднее трение ~ 2 m ≠ Будем считать, однако, что коэффициент трения достаточно велик, чтобы поддерживать максвелл-больцмановское распределение, т. е. остается справедливым c≠=c≠TST Это означает, что частота перехода и константа скорости реакции совпадут с предсказаниями теории переходного состояния.

Теперь пусть коэффициент трения настолько мал, что максвелл-больцмановское распределение не успевает установиться. Это означает, что величина меньше, чем предсказывает теория переходного состояния. Точное решение уравнения дает зависимость константы скорости реакции от коэффициента трения, которая качественно показана на Рис. Можно разбить эту зависимость на три области. В области большого трения (I) константа скорости реакции обратно пропорциональна коэффициенту трения. Это означает, что среда настолько вязкая, что мешает продвижению изображающей точки по координате реакции. В таких условиях протекают реакции крупных частиц в вязких растворителях. В области среднего трения (II) константа скорости химической реакции в жидкости приближается к величине, предсказанной теорией переходного состояния для газа kтпс, однако не достигает этой величины. Это означает, что два приближения, лежащие в основе теории переходного состояния, в действительности не выполняются строго. В области малого трения (III) взаимодействие со средой недостаточно эффективно для поддержания равновесного распределения по энергии.

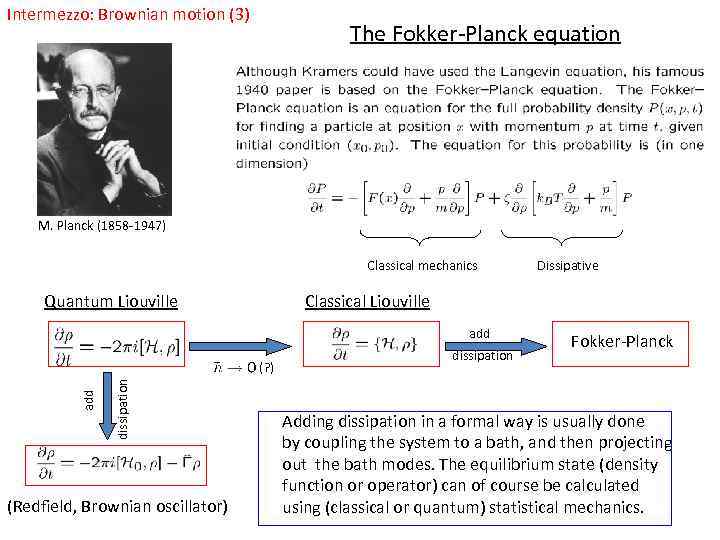Intermezzo: Brownian motion (3) The Fokker-Planck equation M. Planck (1858 -1947) Classical mechanics Quantum Liouville Classical Liouville add dissipation add (? ) (Redfield, Brownian oscillator) Dissipative dissipation Fokker-Planck Adding dissipation in a formal way is usually done by coupling the system to a bath, and then projecting out the bath modes. The equilibrium state (density function or operator) can of course be calculated using (classical or quantum) statistical mechanics.

Возбуждение электронновозбужденных атомов и молекул • Радиационное возбуждение • Электронные возбуждения за счет неупругих столкновений с частицами. • Перенос энергии • Экзотермические химические процессы

Химия возбужденных состояний Электронные возбуждения приводят к: изменению молекулярных орбиталей увеличение энергии изменение характеристик связей и, возможно, к изменению геометрии распределения заряда • возможным изменениям суммарного спина электрона и орбитальной симметрии • • + Þ Изменение связаны с: Þ Временами жизни Þ Электронно донорной / акцепторной способности Þ Кислотности / основности Þ Симметрийными ограничениями на кинетику реакцию Þ Или ограничениями на кинетику реакцию из-за энергии

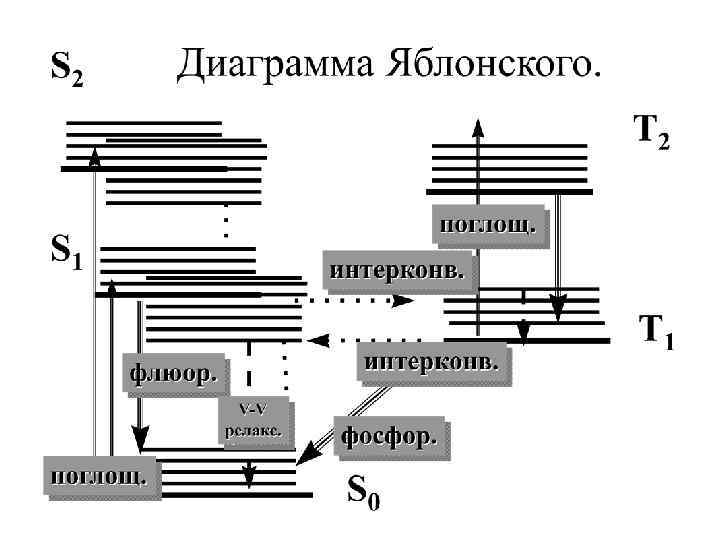
A. Jabłoński Nature 1933, 839

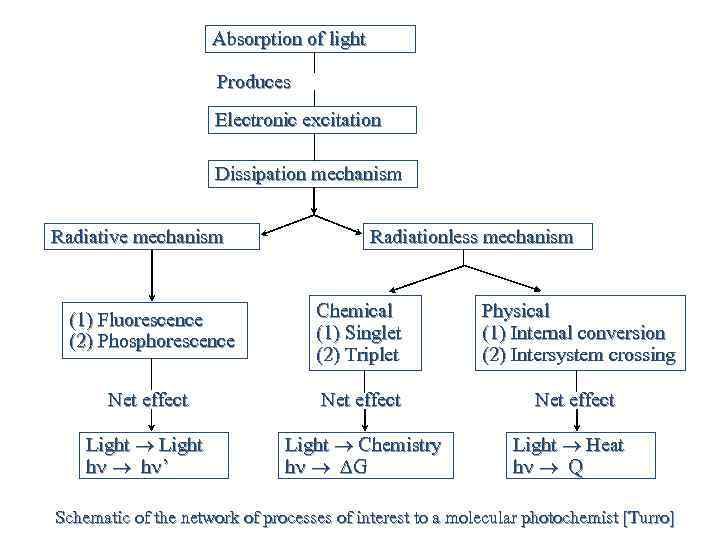Absorption of light Produces Electronic excitation Dissipation mechanism Radiative mechanism Radiationless mechanism (1) Fluorescence (2) Phosphorescence Chemical (1) Singlet (2) Triplet Physical (1) Internal conversion (2) Intersystem crossing Net effect Light h h ’ Light Chemistry h DG Light Heat h Q Schematic of the network of processes of interest to a molecular photochemist [Turro]

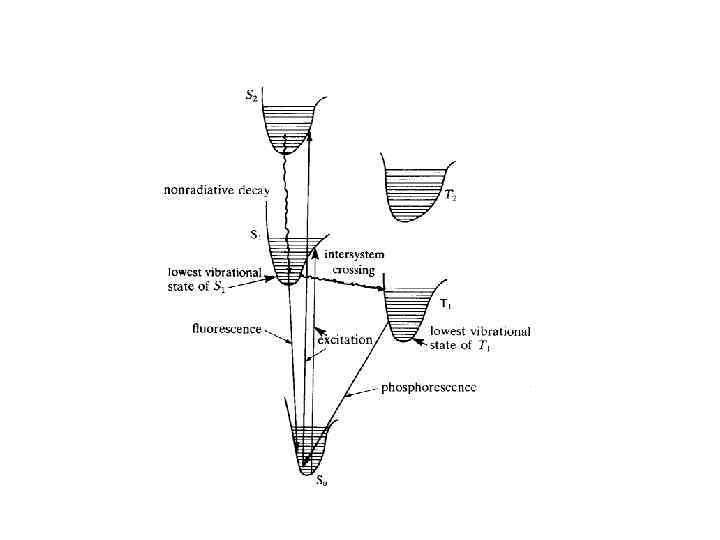10. General principles of photochemistry

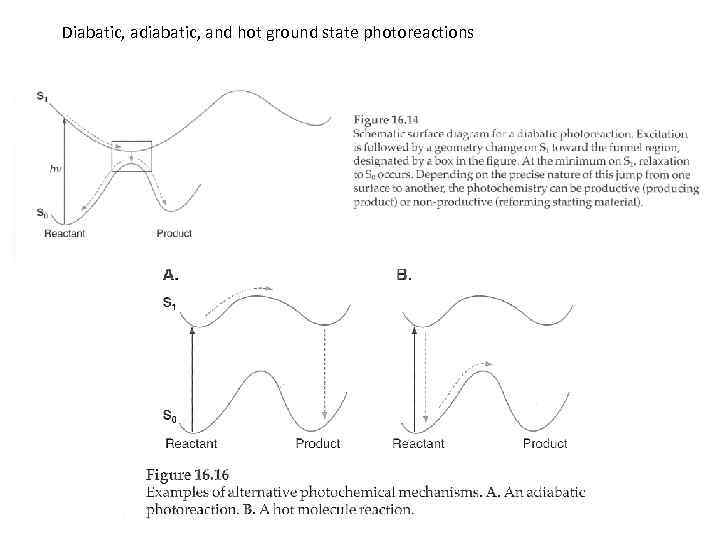Diabatic, adiabatic, and hot ground state photoreactions

Фотохимические процессы • • • Atmospheric and astrophysical chemistry Photosynthesis Lasers Solar energy Semiconductor etching Biological damage – skin cancer etc Vision New chemistry Chemical Dynamics

Всю работу выполняют зеленые растения Перенос энергии фотосинтез Конец активности

зрение

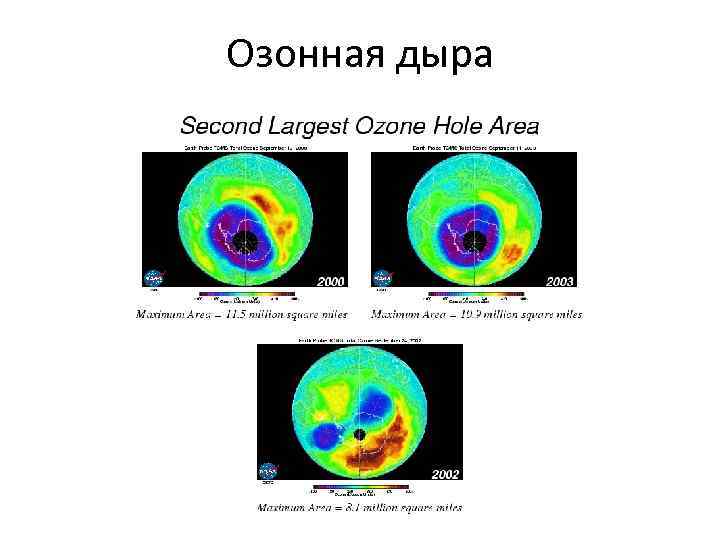Озонная дыра

Здоровье Витамин Д