Фото н — элементарная частица, квант электромагнитного излучения

Фото н — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Заряд фотона также равен нулю. Фотону как элементарной частице свойственен корпускулярно-волновой дуализм, он проявляет одновременно свойства частицы и волны. В вакууме энергия и импульс фотона зависят только от его частоты (или, что эквивалентно, от длины волны): = с/ [м] E = h [Дж] p = h/ =E/c [кг·м/c]

Электромагнитные волны — это поперечные волны, в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, но они существенно отличаются от волн на воде и от звука тем, что их можно передать от источника к приёмнику в том числе и через вакуум.

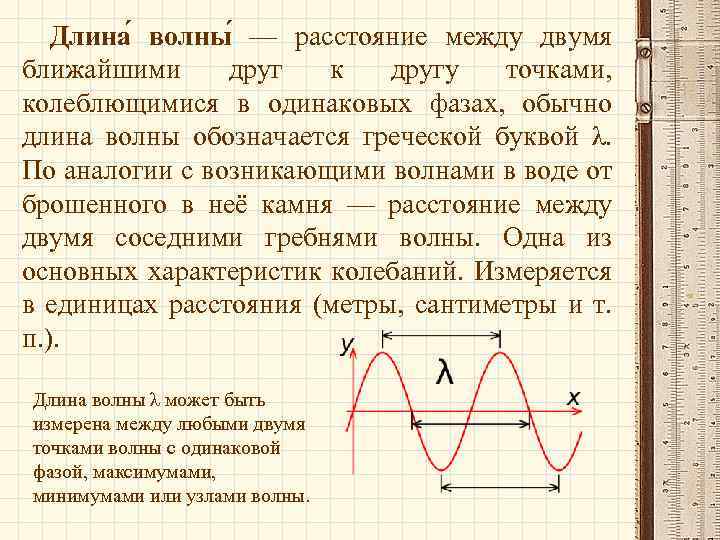Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой λ. По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п. ). Длина волны λ может быть измерена между любыми двумя точками волны с одинаковой фазой, максимумами, минимумами или узлами волны.

Энергетический уровень — возможные значения энергии квантовых систем, то есть систем, состоящих из микрочастиц (электронов, протонов и других элементарных частиц, атомных ядер, атомов и т. д. ) и подчиняющихся законам квантовой механики. Характеризует определённое состояние системы. Различают электронные и внутриядерные энергетические уровни. Современное понятие об орбитальной модели атома, при котором электроны переходят с одного энергетического уровня на другой, а разница между энергетическими уровнями определяет размер выделяемого или поглощаемого кванта света. При этом в промежутках между энергетическими уровнями электроны находиться не могут. Эти промежутки получили название запрещённая энергетическая зона. В качестве примера можно привести электрон в орбитальной модели атома — в зависимости от значений главного квантового числа n и орбитального квантового числа l изменяется уровень энергии, которой обладает электрон. Соответственно каждой паре значений чисел n и l соответствует определённый энергетический уровень.

Статистика Максвелла-Больцмана

Термодинамическое равновесие (тепловое, или статистическое, равновесие) - состояние, в которое приходит любая замкнутая макроскопическая система по истечении достаточно большого промежутка времени. Из детального баланса процессов следует, что при Т. р. реализуется: Максвелла распределение частиц по скоростям, Больцмана распределение частиц по энергиям, Саха формула для степени ионизации атомов и молекул, закон действующих масс для хим. равновесия, Планка закон излучения, Кирхгофа закон излучения, Стефана-Больцмана закон излучения и т. д. Термодинамически равновесное поле излучения можно получить внутри замкнутой полости с теплоизолирующими стенками. Внутри такой полости фотоны распределены однородно и изотропно, интенсивность излучения определяется формулой Планка , а поток излучения строго равен нулю.

Распределение Больцмана - распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия. Согласно Б. р. , число частиц ni с полной энергией Еi равно: где gi - статистич. вес (число возможных состояний частицы с энергией Еi). Постоянная А находится из условия, что сумма ni по всем возможным значениям i равна заданному полному числу частиц N в системе (условие нормировки): В случае, когда движение частиц подчиняется классич. механике, энергию Е i можно считать состоящей из кинетич. энергии Еi(кин) частицы (молекулы или атома), её внутр. энергии Еi(вн) (напр. , энергии возбуждения электронов) и потенциальной энергии Еi(пот) во внешнем поле, зависящей от положения частицы в пространстве: Еi = Еi(кин) + Еi(вн) + Еi(пот)

В астрофизике, особенно в теории звездных спектров, распределение Больцмана используется для определения относительной заселенности электронами различных уровней энергий. Если обозначить индексами 1 и 2 два энергетич. состояния атома, то из Б. р. следует: Формула Больцмана Распределение частиц по скоростям (Максвелла распределение) является частным случаем распределения Больцмана. Оно имеет место, когда можно пренебречь внутренней энергией возбуждения Еi(вн) и влиянием внеш. полей Еi(пот). k = 1, 380658 10 -23 Дж/K – постоянная Больцмана

Распределение Максвелла - распределение частиц (молекул, атомов) идеального газа но скоростям в условиях термодинамического (теплового) равновесия. Согласно данному распределению, среднее число частиц, имеющих абсолютную величину скорости в интервале от v до v, определяется выражением: где N - полное число частиц в системе. М. р. получило прямое подтверждение в серии опытов с молекулярными пучками. Кроме того, закономерности протекания целого ряда физ. процессов в газах убедительно свидетельствуют о справедливости М. р. (напр. , доплеровское уширение спектр. линий, особенности ионизации атомов и диссоциации молекул). Частицы с таким распределением по скоростям подчиняются классической статистике или статистики Максвелла-Больцмана.

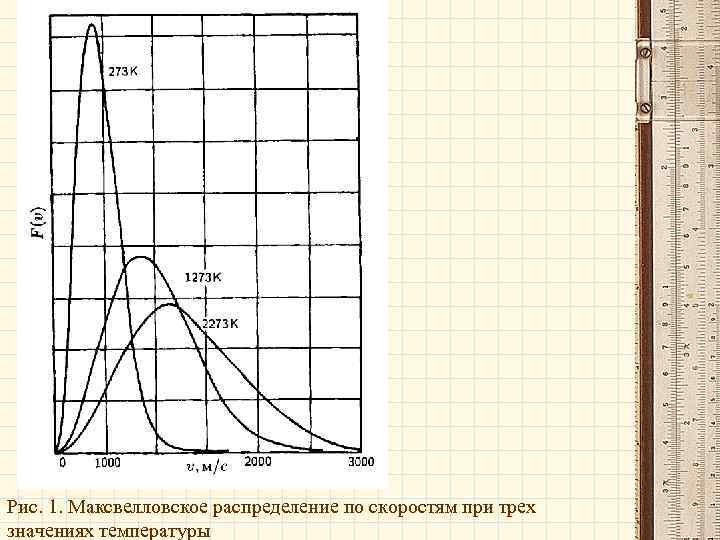Рис. 1. Максвелловское распределение по скоростям при трех значениях температуры

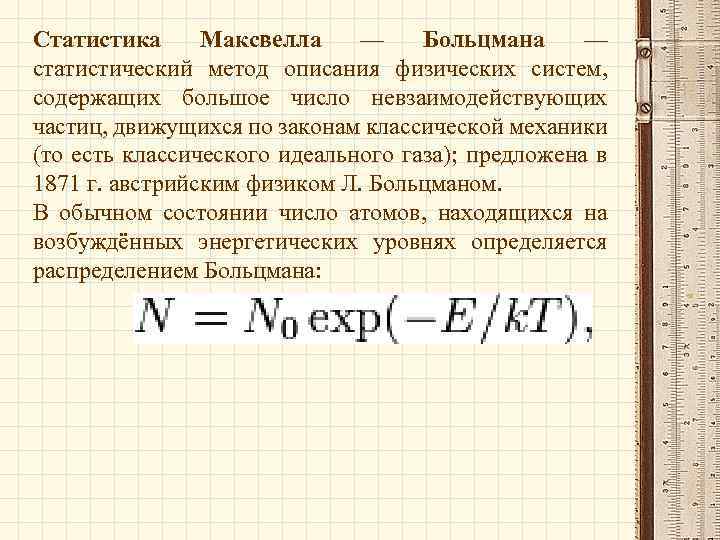Статистика Максвелла — Больцмана — статистический метод описания физических систем, содержащих большое число невзаимодействующих частиц, движущихся по законам классической механики (то есть классического идеального газа); предложена в 1871 г. австрийским физиком Л. Больцманом. В обычном состоянии число атомов, находящихся на возбуждённых энергетических уровнях определяется распределением Больцмана:

№ 1 Задачи: Найдите относительную заселенность верхнего энергетического уровня по сравнению с нижним, если они находятся в термодинамическом равновесии и если энергетический зазор между уровнями соответствует частоте генерации CO 2 лазера ( = 10, 6 мкм) в случае температуры 300 К. Учесть, что h /k = 14, 3 10 -3/ , K, где в микрометрах.

№ 2 Задачи: В условиях теплового равновесия при Т = 300 К отношение населенностей n 2/n 1 некоторой пары уровней равно 1/е. Рассчитайте частоту перехода между ними. В какой диапазон спектра электромагнитных волн она попадает?

№ 3 Задачи: Уровни 1 и 2 находятся на таком расстоянии по энергии, что частота соответствующего перехода попадает в середину видимого диапазона. Рассчитайте равновесное отношение населенностей этих двух уровней при комнатной температуре.