Формулы структурной кристаллографии Представление кристалла в обратном пространстве

Зарегистрируйтесь, чтобы просмотреть полный документ!

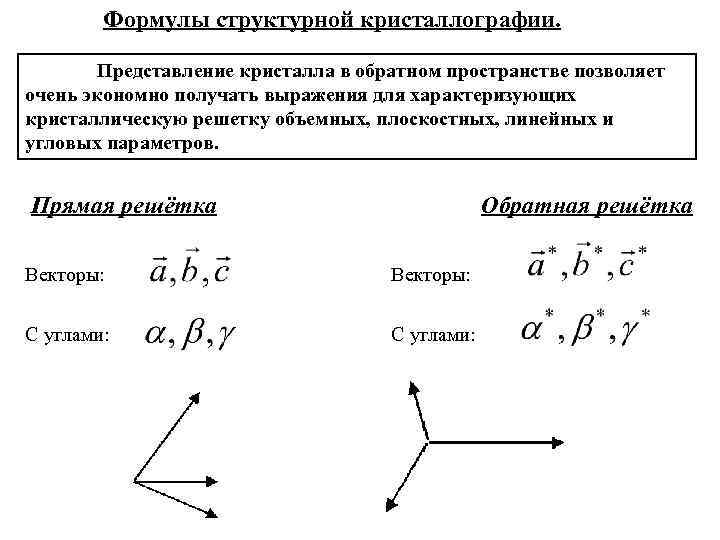
Формулы структурной кристаллографии. Представление кристалла в обратном пространстве позволяет очень экономно получать выражения для характеризующих кристаллическую решетку объемных, плоскостных, линейных и угловых параметров. Прямая решётка Обратная решётка Векторы: С углами:

1. Определение межплоскостного расстояния обратной решетки ghkl. dhkl по вектору Для кубической сингонии

2. Определение периода идентичности Iuvw вдоль направления [uvw]. - прямой вектор Для кубической сингонии

3. Определение расстояния между двумя узлами решетки, заданными их базисами: В уравнение для периода идентичности подставим вместо индексов прямой, соединяющей эти узлы разности их базисов. Для кубической сингонии

4. Определение площади элементарной петли плоской узловой сетки (hkl) Для кубической сингонии

5. Определение угла между плоскими узловыми сетками (h 1 k 1 l 1), (h 2 k 2 l 2) Скалярное произведение Для кубической сингонии

6. Определение угла между двумя узловыми прямыми [u 1 v 1 w 1], [u 2 v 2 w 2] Скалярное произведение Для кубической сингонии

7. Определение угла между направлением [uvw] Для кубической сингонии и плоскостью (hkl)

8. Связь между индексами плоскости (hkl) и индексами лежащего в нем направлении [uvw]. 9. Определение индексов плоскости (hkl) по индексам лежащих в ней направлений [u 1 v 1 w 1], [u 2 v 2 w 2].

10. Определение индексов направления [uvw] по индексам плоскостей, пересекающихся по этому направлению. (h 1 k 1 l 1) [uvw] (h 2 k 2 l 2) Правило для определения индексов: h 1 k 1 l 1 k 1 l 1 h 1 k 1 h 2 k 2 l 2 k 2 l 2 h 2 k 2 (k 1 l 2 –k 2 l 1): (l 1 h 2 –l 2 h 1): (h 1 k 2 –h 2 k 1) u v w

Скачать презентацию Формулы структурной кристаллографии Представление кристалла в обратном пространстве

Крист_лк17.ppt

Количество слайдов: 10