Формулы позволяющие выразить sin 2 x cos 2

Формулы, позволяющие выразить sin 2 x, cos 2 x, tg 2 x через sin x, cos x, tg x, называют формулами двойного аргумента.

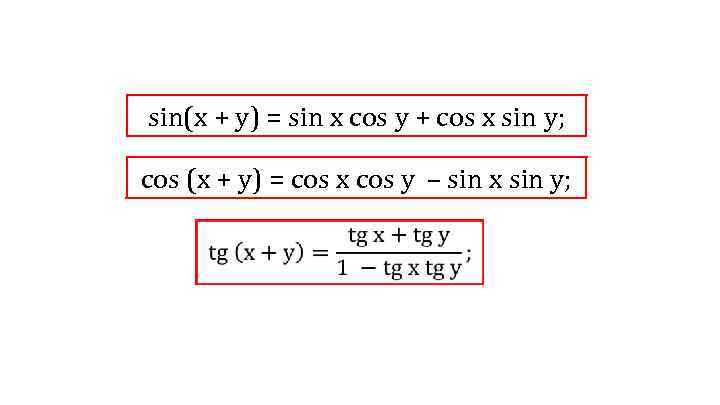sin(x + y) = sin x cos y + cos x sin y; cos (x + y) = cos x cos y – sin x sin y;

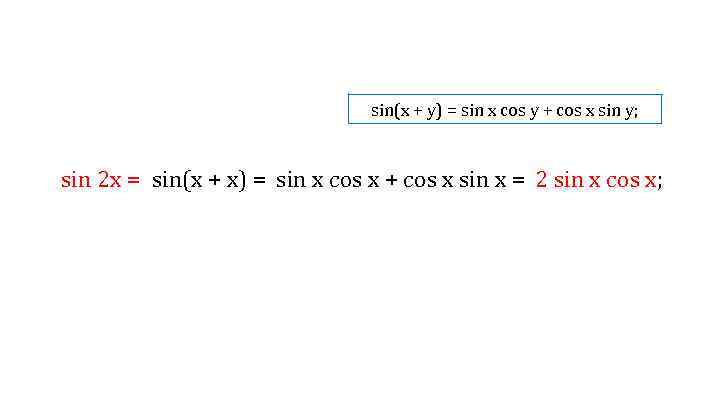sin(x + y) = sin x cos y + cos x sin y; sin 2 x = sin(х + х) = sin х cos x + cos x sin х = 2 sin х cos x;

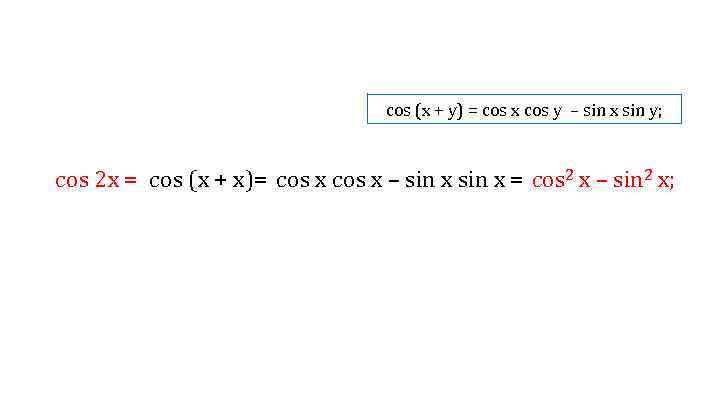cos (x + y) = cos x cos y – sin x sin y; cos 2 x = cos (х + х)= cos х – sin х = cos 2 х – sin 2 х;

tg 2 x = tg (х + х) =

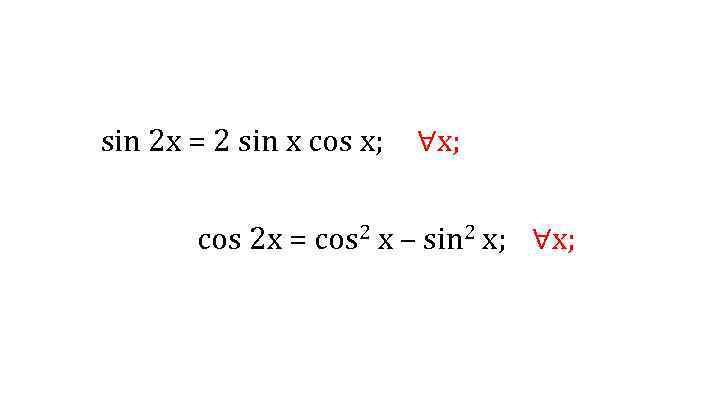sin 2 x = 2 sin х cos x; ∀x; cos 2 x = cos 2 х – sin 2 х; ∀x;

Решение. 1 = cos 2 х + sin 2 х; а 2 – b 2 = (a – b)(a + b) а 2 – 2 ab + b 2 = (a – b)2

Решение. cos 2 х + sin 2 х=1

Решение. 15° = 90° – 750;

Пример 4. Решить уравнение sin 6 x + cos 3 x = 0. Решение. sin 6 x = sin 2 ∙ 3 x; sin 2 ∙ 3 x + cos 3 x = 0; 2 sin 3 x cos 3 х + cos 3 x = 0; cos 3 x (2 sin 3 х + 1) = 0; cos 3 x = 0; или 2 sin 3 х + 1 = 0; 2 sin 3 х = – 1;