Формулы комбинаторики Лекция 3 Комбинаторные задачи Задачи

Формулы комбинаторики Лекция 3

Комбинаторные задачи Задачи, в которых из элементов некоторого конечного множества нужно составить комбинации, обладающие теми или иными свойствами, и посчитать число таких комбинаций, называются комбинаторными. Раздел математики, в котором они рассматриваются, называется комбинаторикой.

Основные правила комбинаторики Правило суммы Правило произведения

Правило суммы Если элемент a можно выбрать m способами, а элемент b – n способами, причем любой выбор элемента a отличен от любого выбора элемента b, то выбор « a или b » можно выполнить m+n способами.

Пример На первой полке книжного шкафа расположено 40 книг, а на второй – 30. Все книги различны. Сколькими способами можно выбрать одну книгу с этих 2 полок? Ответ: 40+30=70

Правило суммы Теорема 1 Если конечные множества и не пересекаются, то число элементов в их объединении равно сумме элементов этих множеств

Правило произведения Если элемент a можно выбрать m способами, а элемент b – n способами, то число способов выбрать пару (a, b) равно mn.

Декартово произведение Пусть Декартовым произведением множеств и называется

Правило произведения Теорема 2 Для конечных множеств и

Доказательство Для множеств и элементы : … выпишем все

Доказательство Получили

Правила суммы и произведения могут быть обобщены на случай большего числа множеств и доказаны методом математической индукции.

Пример Сколько существует пятизначных чисел? Решение. Первая цифра любого пятизначного числа может быть любой, кроме нуля, то есть выбирается из множества

Решение Вторая, третья, четвертая и пятая цифры выбираются из множества всех цифр Каждое пятизначное число – упорядоченный набор 5 цифр числа, то есть число пятизначных чисел равно количеству элементов множества , то есть

Пример Сколько существует пятизначных чисел, кратных 5? Решение. Первая цифра любого пятизначного числа может быть любой, кроме нуля, то есть выбирается из множества

Вторая, третья и четвертая цифры выбираются из множества всех цифр Пятая цифра может быть либо 5, либо 0, то есть выбирается из множества Поэтому число пятизначных чисел равно

Замечание Приведенные решения демонстрируют, как используется правило произведения при решении задач. Обычно множества, из которых выбираются некоторые элементы, даже не вводятся, нужно просто знать число элементов этих множеств.

Существуют и другие решения рассмотренных задач. Число всех пятизначных чисел может быть найдено как разность между числом всех чисел от 1 до 99999 и числом чисел от 1 до 9999 (не являющимися пятизначными), то есть 99999 -9999=90000.

Число пятизначных чисел, кратных 5, равно так как на 5 делится каждое пятое число.

Выборки Пусть. Любой набор n элементов из множества A будем называть выборкой объема n. Если элементы в выборке не повторяются, то выборка называется бесповторной, в противном случае – с повторениями.

Выборка называется упорядоченной, если в выборке важен порядок расположения элементов, в противном случае выборка называется неупорядоченной. Например, любое трехзначное число является упорядоченной выборкой объема 3 из множества.

Любое пятибуквенное слово, записанное на русском языке, является упорядоченной выборкой объема 5 из множества, содержащего все буквы русского алфавита. Если буквы в слове не повторяются – выборка бесповторная (например, слово «цифра» ), если же есть хотя бы 2 одинаковых буквы, то выборка с повторениями (например, слово «холод» ).

Сочетания и размещения Неупорядоченные выборки в комбинаторике называются сочетаниями, упорядоченные – размещениями.

Размещения Упорядоченные выборки объема n из множества, содержащего m элементов, называются размещениями из m элементов по n.

Число размещений из m элементов по n без повторений обозначается (А – первая буква французского слова arrangement – размещение, приведение в порядок). Число размещений из m элементов по n с повторениями обозначается.

Пример Составить размещения без повторений из элементов множества по 3 элемента. Решение

Теорема 3 Число размещений без повторений из m элементов по n определяется по формуле

Доказательство Число равно числу всех бесповторных упорядоченных выборок объема n из m элементов. В качестве первого элемента можно взять любой элемент множества, поэтому число способов выбрать первый элемент равно m.

Второй элемент из оставшихся элементов можно выбрать числом способов и т. д. ; n - й элемент можно выбрать из оставшихся элементов числом способов. По правилу произведения, получаем

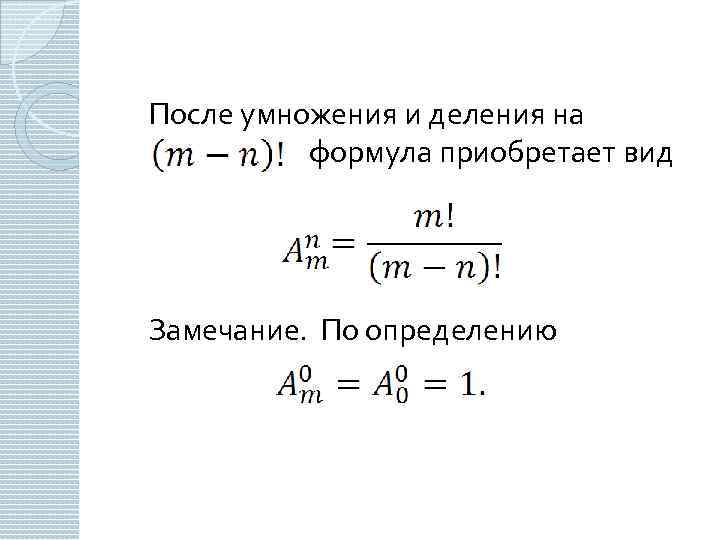
После умножения и деления на формула приобретает вид Замечание. По определению

Пример Сколькими способами можно составить расписание из 6 различных уроков, если всего изучается 10 предметов? Расписание – упорядоченная бесповторная выборка объема 6 из 10 предметов, то есть размещение из 10 по 6.

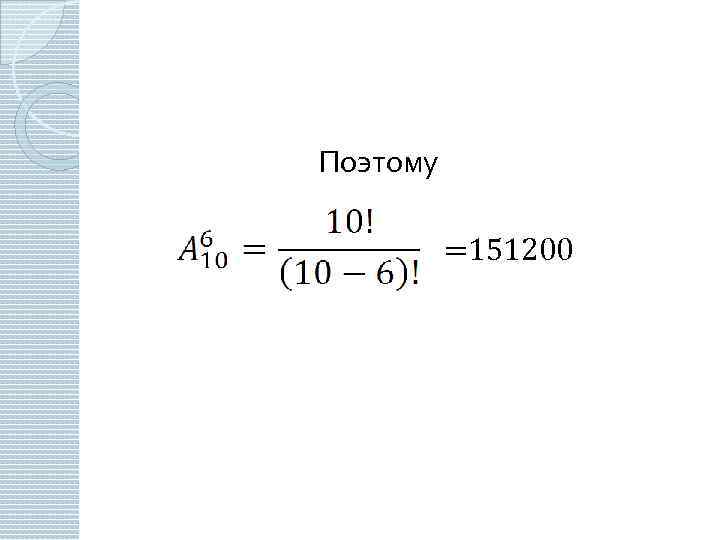
Поэтому =151200

Теорема 4 Число размещений с повторениями из m элементов по n определяется по формуле

Доказательство Число способов выбрать каждый элемент выборки равно m. Поэтому в соответствии с правилом произведения

Пример На рояле 88 клавиш. Сколькими способами можно последовательно извлечь 3 звука? Ответ:

Перестановки без повторений Размещения без повторений из m элементов по m называются перестановками без повторений из m элементов. Число перестановок без повторений из m элементов обозначается (буква P – первая буква французского слова permutation – перестановка). По определению

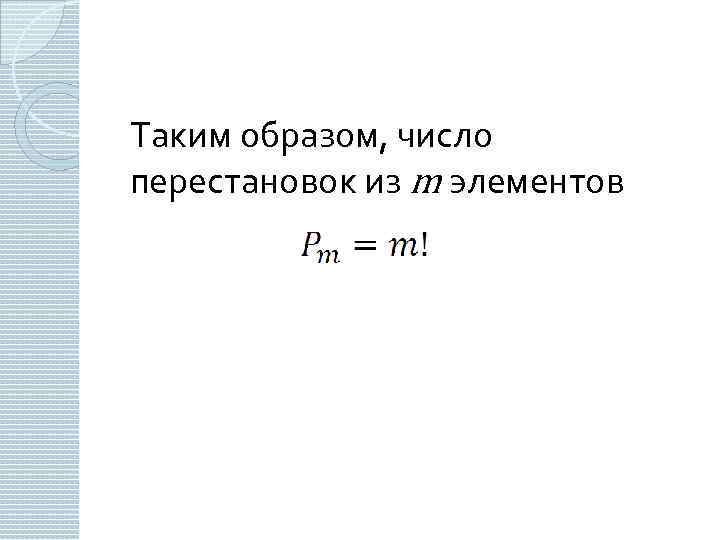
Таким образом, число перестановок из m элементов

Пример Сколько перестановок без повторений можно получить из букв, составляющих слово «апельсин» ? Ответ: 8!=40320

Пример Собрание сочинений Джека Лондона состоит из 7 томов. Сколькими способами можно разместить эти 7 томов на книжной полке? Сколькими способами их можно расставить так, чтобы первый и второй тома стояли рядом?

Решение Ответ: 7!=5040; 2!6!=1440. Указание. «Склеиваем» первые два тома (это можно сделать 2! числом способов), расставляем 6 книг на полке.

Сочетания без повторений Неупорядоченные бесповторные выборки объема n , составленные из элементов множества, содержащего m элементов, называются сочетаниями без повторений из m элементов по n. Число сочетаний без повторений из m элементов по n обозначается (C – первая буква французского слова combination – сочетание).

Пример Составить сочетания без повторений из элементов множества по 3 элемента. Ответ:

Теорема 5 Число сочетаний без повторений из m элементов по n определяется по формуле

Доказательство Если составить все неупорядоченные выборки объема n из m элементов без повторений и совершить в каждой всевозможные перестановки, то получим все размещения из m элементов по n. Поэтому

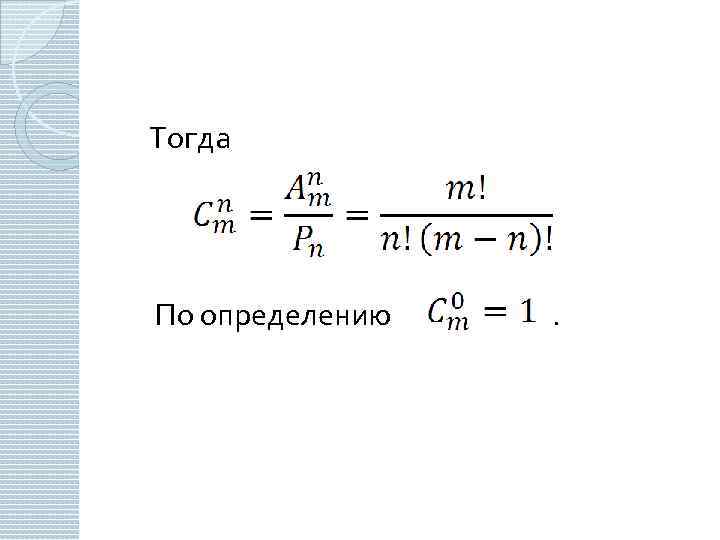
Тогда По определению .

Пример Сколькими способами можно составить команду из четырех человек для участия в соревнованиях по бегу, если имеется 7 спортсменов? Ответ:

Свойства чисел 1. Свойство симметрии 2. Свойство Паскаля 3. Бином Ньютона.

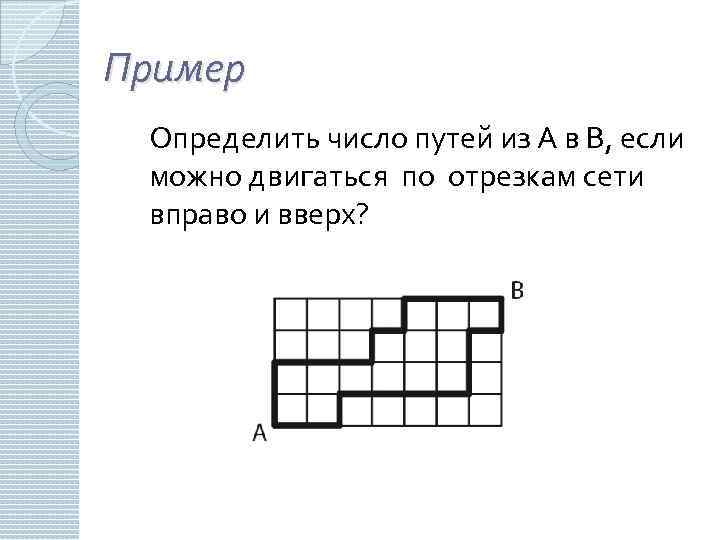
Пример Определить число путей из А в В, если можно двигаться по отрезкам сети вправо и вверх?

Решение Обозначим один шаг вправо x, вверх – y. Тогда любой путь из А в В – последовательность из 11 букв, каждая из которых либо x, либо y. Тогда выделенным на рисунке путям соответствуют последовательности xxyxxxxyyxy; yyxxxyxyxxx. Число различных путей равно числу сочетаний из 11 по 4.