Formal Verification Lecture 9 Formal Verification l

Formal Verification Lecture 9

Formal Verification l Formal verification relies on l l l Descriptions of the properties or requirements Descriptions of systems to be analyzed, and Verification techniques showing requirements are met by system description l Rely on underlying mathematical logic system and the proof theory of that system

Formal Approach l Formal Models use language of mathematics l Specification languages l l l For policies, models and system descriptions Well-defined syntax and semantics – based on maths Current trends - two general categories l l Inductive techniques Model checking techniques l Differences based on § Intended use, degree of automation, underlying logic systems, etc.

Verification techniques – Criteria for classifying l Proof-based vs model-based l Proof: Formula define premises / conclusions l l Model-based: l l Proof shows how to reach conclusions from premises Premises and conclusions have same truth tables Degree of automation l manual or automated (degree)

Propositional logic

Verification techniques – Criteria for classifying l Full verification vs property verification l l Does methodology model full system? Or just prove certain key properties? l l Intended domain of application l l Examples? HW/SW, reactive, concurrent Predevelopment vs post development l As design aid or after design

Inductive verification l l Typically more general Uses theorem provers l l l E. g. , uses predicate calculus A sequence of proof steps starting with premises of the formula and eventually reaching a conclusion May be used l l To find flaws in design To verify the properties of computer programs

Model-checking l Systems modeled as state transition systems l l l Properties are formulas in logic l l Truth values are dynamic Show: Model and the desired properties are semantically equivalent l l Formula may be true in some states and false in others Formulas may change values as systems evolve Model and properties express the same truth table Often used after development is complete but before a product is release to the general market l Primarily for reactive, concurrent systems

Formal Verification: Components l Formal Specification l defined in unambiguous (mathematical) language l Restricted syntax, and well-defined semantics based on established mathematical concepts § l l l Example: ? Implementation Language l Generally somewhat constrained Formal Semantics relating the two Methodology to ensure implementation ensures specifications met

Specification Languages l Specify WHAT, not HOW l l Valid states of system Postconditions of operations Non-Procedural Typical Examples: l l l Propositional / Predicate Logic Temporal Logic (supports before/after conditions) Set-based models (e. g. , formal Bell-La. Padula)

Specification Languages l Must support machine processing l l l Strong typing Model input/output/errors Example: SPECIAL l l First order logic based Strongly typed VFUN: describes variables (state) OFUN/OVFUN: describe state transitions

Example: SPECIAL l l l MODULE Bell_La. Padula_Model Give_read Types Subject_ID: DESIGNATOR; Object_ID: DESIGNATOR; Access_Model: {READ, APPEND, WRITE}; Access: STRUCT_OF(Subject_ID subject; Object_ID object; Access_Mode mode); Functions VFUN active (Object_ID object) -> BOOLEAN active: HIDDEN; INITIALLY TRUE; VFUN access_matrix() -> Access accesses: HIDDEN; INITIALLY FORALL Access a: a INSET accesses => active(a. object); OFUN give_access(Subject_ID giver; Access access); ASSERTIONS active(access. object) = TRUE; EFFECTS `access_matrix() = access_matrix() UNION (access); END_MODULE

Example: Enhanced Hierarchical Development Methodology l Based on HDM l l l A general purpose design and implementation methodology Goal was l To mechanize and formalize the entire development process l Design specification and verification + implementation specification and verification Proof-based method l Uses Boyer-Moore Theorem Prover

Example: Enhanced Hierarchical Development Methodology l Hierarchical approach l Abstract Machines defined at each level l specification written in SPECIAL Mapping Specifications define functionality in terms of machines at higher layers Consistency Checker validates mappings “match” l Compiler that maps a program into a theorem-prover understood form l Successfully used on MLS systems l Few formal policy specifications outside MLS domain

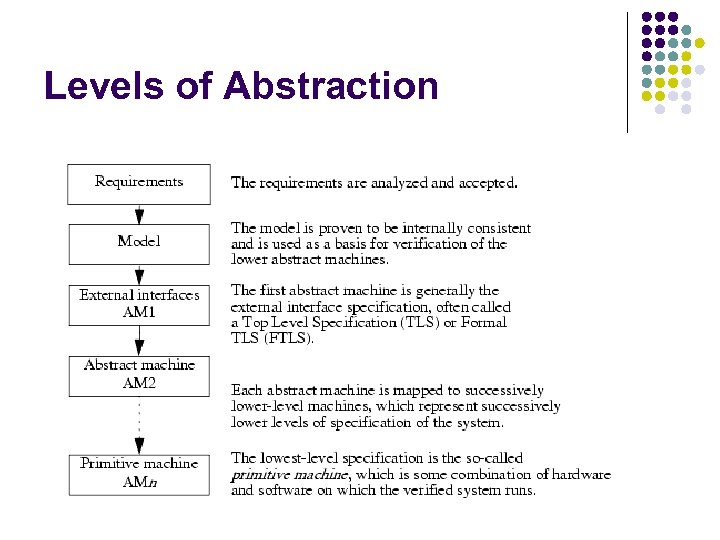Levels of Abstraction

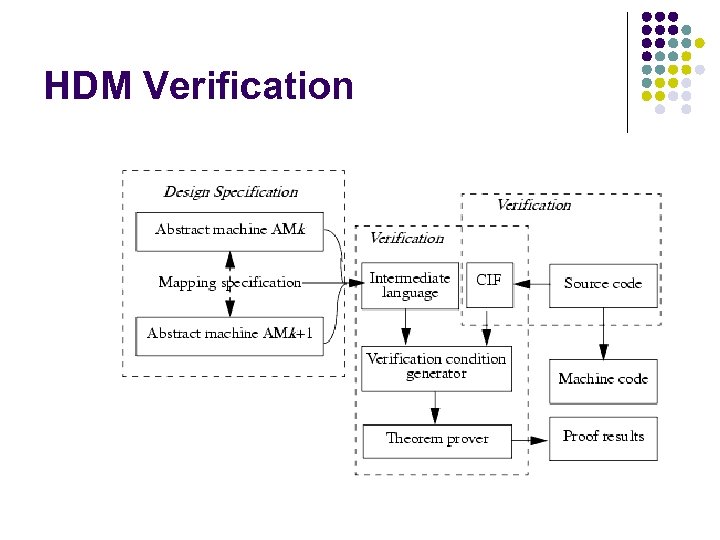HDM Verification

Boyer-Moore Theorem Prover l Fully automated l l No interface for comments or directions User provides all theorems, axioms, lemmata, assertions l l l LISP like notation Very difficult for proving complex theorems Key idea l l Used extended propositional calculus Efficiency – to find a proof.

Boyer-Moore Theorem Prover l Steps: l l l Simplify the formula Reformulate the formula with equivalent terms Substitute equalities Generalize the formula by introducing variables Eliminate irrelevant terms Induct to prove

Gypsy verification environment (GVE) l Based on Pascal l l Specifications defined on procedures l l Formal proof and runtime validation support Entry conditions, Exit conditions, Assertions Proof techniques ensure exit conditions / assertions met given entry conditions l Also run-time checking Examples: § § § Gypsy (in book) – uses theorem prover CLU Eiffel (and derivatives) – run-time checks

Other Examples l Prototype Verification System (PVS) l l l Based on EHDM Interactive theorem-prover Symbolic Model Verifier l l l Temporal logic based Notion of “path” – program represented as tree Statements that condition must hold at a future state, all future states, all states on one path, etc.

Other Examples l Formal verification of protocols l l l Verification of libraries l l l Key management Protocol development Entire system not verified But components known okay High risk subsystems

Protocol Verification l l Generating protocols that meet security specifications Assumes cryptography secure l But cryptography is not enough