Formal verification in Embedded System design Dr Abhik

Formal verification in Embedded System design Dr. Abhik Roychoudhury School of Computing abhik@comp. nus. edu. sg

Safety Critical Systems Ø Ø Ø Safety Ø Design invariants must always hold in all executions of the system. Critical Ø Violating invariants in any execution can be disastrous. Examples Ø Air traffic controller Ø Automobile parts.

Methodological view point Ø Ø Inject higher reliability in design life cycle. Safety critical systems often have a computer component. This trend is increasing with growth of embedded applications. What kind of computer systems are they ?

Reactive Systems Ø Ø Ø Continuously interacts with its environment. Interaction with env. is asynchronous. Often, its response to environment needs to obey time constraints. Often consists of a concurrent composition of processes. [Harel]

Why study them now ? Ø Embedded systems Ø Ø Many of them safety-critical Ø Ø Using a computer component as part of a bigger system becoming pervasive. e. g. automobile parts Difficulty in using Current verif. techniques Ø Ø Lack of tool support for reliable modeling. Perceived as intrusive to design process.

Validation Techniques Ø Ø In circuit Emulator (ICE) Logic Analyzer Model based simulation Formal verification techniques Ø Ø Ø Model Checking Deduction Combinations of the two

In circuit Emulator (ICE) 1. 2. 3. Used widely in industry for designs where a microproc. interacts with potpourri of peripherals. ICE is a dedicated hardware for a particular processor which allows its internals to be read. Response of processor (to environment) observed by physically replacing chip with ICE.

Logic Analyzer § § § Used for sampling many signals simultaneously in a complex design. Can snoop on a bus to observe interactions of a microprocessor with its environment. ICE and Logic Analyzer do not work when: § Processor, peripherals, bus all integrated in a chip. § System-on-Chip (So. C) – Current industry trend.

Model based simulation Ø Ø Ø Simulate and observe the behaviors of a system model, rather than the system itself. Takes validation/debugging higher in the design lifecycle. Since a model is validated, can take place prior to system integration Ø Hardware software co-simulation (POLIS) [Earlier lecture]

Model Checking – What ? n Same as model based simulation except that you check all possible behaviors. Needed for checking critical properties. Can be used if model has finite states. n Many realistic systems are infinite-state n n e. g. real-time systems. For these systems, extensions of model checking.

Spec. and Impl. n n n Need a specification language (property to be verified). Need an implementation language (system to be verified) Such a language describes reactive system behaviors. n Temporal Logic n n n Process Algebra/Calculus n n n Linear - LTL Branching - CTL CCS (Milner 1989) CSP (Hoare) Finite state automata over infinite inputs.

Model Checking – How ? n Inputs: n n n Output: n n n finite state concurrent system (implementation as FSM) Temporal logic formula (specification language) True if the specification holds A counterexample behavior if it does not Technique: n n Implementation FSM is a finite graph. Unfold and search this finite graph to check all behaviors.

State space explosion n n Model checking invariant properties = Reachability computation Requires visiting reachable set of states (state space). If a circuit has 100 latches, then maximum 2^100 states. Visiting and enumerating all these states is inefficient n n Space Time also. n Explicit state model checking quickly runs out of MM. n Need a symbolic representation of the state space.

Symbolic representation n Any state s is an True/false assignment of boolean variables. n n This induces a boolean function on these boolean vars. n n n ( X 1 X 2 X 3) ( X 1 X 2 X 3) A canonical representation of this boolean function implicitly encodes set of states (call it Binary Decision Diagram) n n X 1 X 2 X 3 Any set of states is also equivalent to a boolean function n n X 1 = false , X 2 = true, X 3 = false X 1 X 2 A similar encoding can be obtained for transition relation also. [Mc. Millan et. al. ]

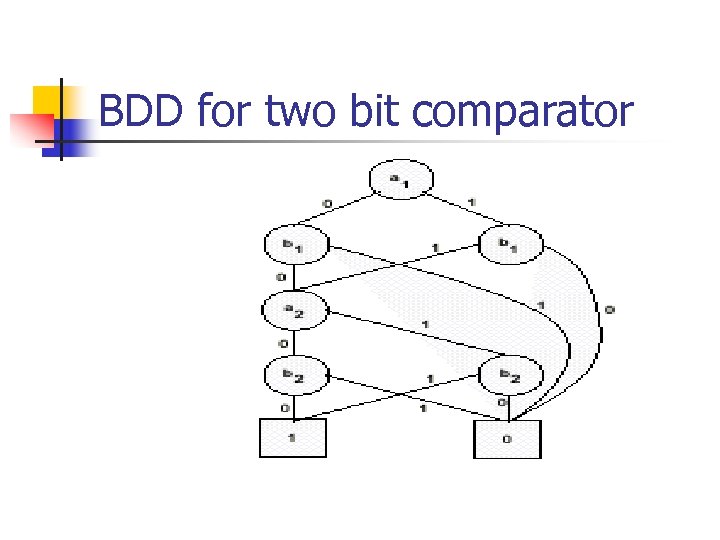
BDD for two bit comparator

Model Checkers n Formal. Check (Commercialized by Cadence) n n n Symbolic Model Verifier (CMU) n n Internal representation : BDD Mur (Stanford) n n n Synchronous input language Based on automata Asynchronous interaction via shared variables Explicit state model checker SPIN (Bell Labs) n Validation of Protocols/Software

Beyond finite state n Model Checking restricted to finite state systems. n Sources of non-finiteness in reactive emb. Sys. n n n Data values from unbounded domain - counters Unbounded data paths Real Variables, in particular timers Unbounded number of similar components Partial specification for some of the system components How to verify such systems ?

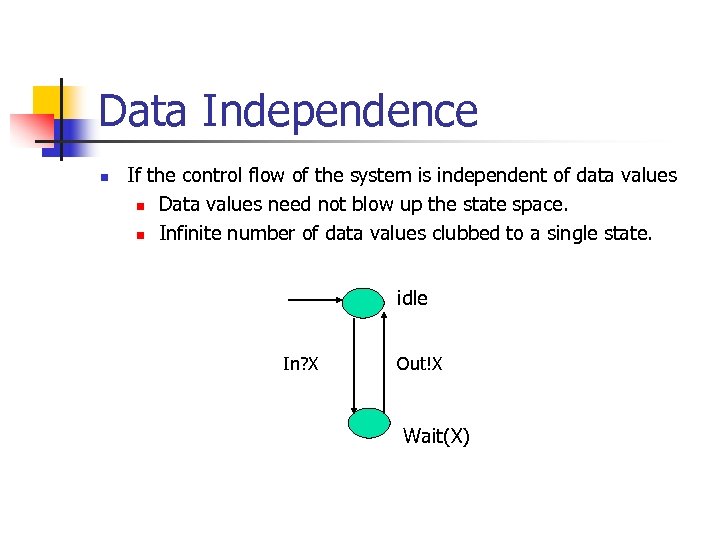
Data Independence n If the control flow of the system is independent of data values n Data values need not blow up the state space. n Infinite number of data values clubbed to a single state. idle In? X Out!X Wait(X)

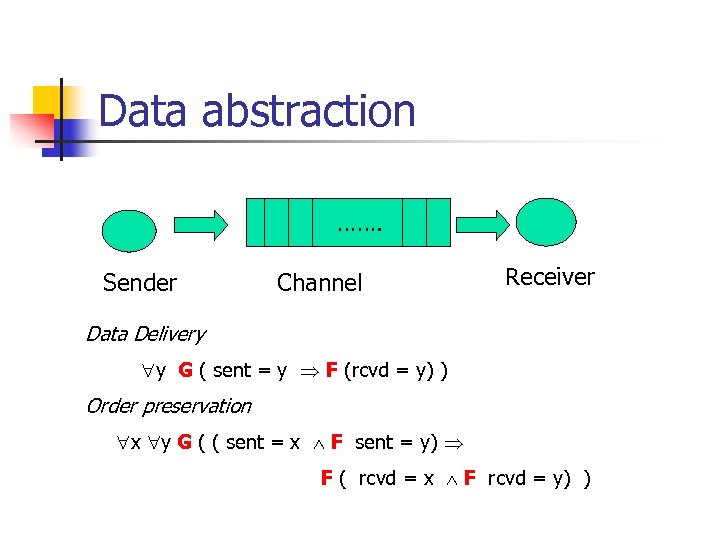
Data abstraction ……. Sender Channel Receiver Data Delivery y G ( sent = y F (rcvd = y) ) Order preservation x y G ( ( sent = x F sent = y) F ( rcvd = x F rcvd = y) )

Data abstraction n n Cannot collapse all data values into a single value. Choose the abstract data domain based on the property n n n Such data abstractions are routine and can be automated from n n n Data Delivery : { y, y} Order Preservation : { x, y, {x, y} } System to be verified Property to be verified (data delivery/ order preservation here) Abstraction techniques for unbounded data paths n The Channel in this example could be unbounded.

Real time systems n Popular representation : timed automata [Alur et. al. ] n n n n Finite state automata Augmented with finite set of real valued timers Transitions in the automata occur in zero time. Time can elapse in states : Delay transitions State space of a timed automata is infinite. Finite representation obtained by constructing “timer regions” Construct region graph where each node is a region. Model Checking via searching this region graph.

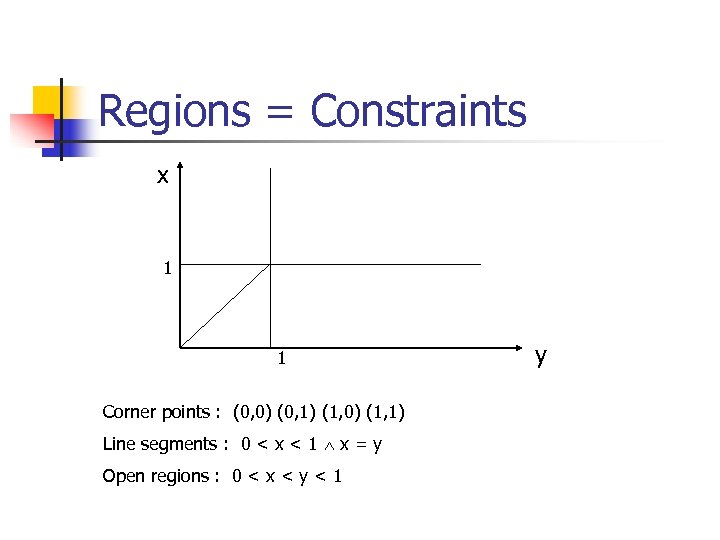
Regions = Constraints x 1 1 Corner points : (0, 0) (0, 1) (1, 0) (1, 1) Line segments : 0 < x < 1 x = y Open regions : 0 < x < y < 1 y

Parameterized systems n Infinite family of finite state systems n n n N process cache coherence protocol N process distributed algorithm (for mutual exclusion) A hardware arbiter for resource shared among N processes n Number of processes in the system to be verified is unbounded. n Non-finiteness is not due to data. n Verification is undecidable (no algorithm may exist).

That old trick ! n n A network of N similar processes. Each process has the same finite state automata n n { s 0, s 1, …, sk} Define a finite vector cnt 0, cnt 1, …, cntk n Cnt 0 = Number of processes in state s 0 n Such a vector defines a state of the entire network. Constraints on cnt 0, cnt 1, …, cntk now define regions. n If the number of regions in your problem is finite, n n Can construct and search finite region graph (Model Checking)

Induction n Example: System : n bit shift register Initial state : Data fed at left end property: F out (Data popped at right end) n Cannot construct a uniform proof ( for any n) Natural to induct on the number of bits. n Induction on process structure (not just number of processes) n n n Tree networks (e. g. System Buses arranged hierarchically) Combining limited induction with search (as in Model Checking).

FV for ES – The reality n Is it any different ? n Current verif. Techniques should scale up for ES Hardware. n Embodies hardware/software interaction: often real-time. n Reuse of vendor provided IP blocks n n Implementation not known for Intellectual property reasons No single person/team knows the entire design.

FV for ES – Consequences n Wealth of model checkers (with limited deduction) useful for ES hardware verification n n Handle state-of-the-art superscalar processors with n Out-of-order execution n Speculative execution ES component interaction is fairly detailed, low-level and often specified in hard-to-read manuals. n n Real-time verification is not yet a mature technology. Need to reliably model software-hardware interfaces.

FV for ES - Consequences n A realistic ES design typically consists of: n n Number of IP blocks Connected to one/more system bus via bridges n View an IP block as a hardware subroutine – Need REUSE. n Reuse IP blocks designed by others (and provided by vendors). n Each IP block comes with interface specification n n Input and output signals Some timing diagrams

FV for ES - Techniques n n Model Checking (Not the panacea) Abstraction n Data abstraction on integer counters useful n Routine control abstractions – based on symmetry etc. n A process of gradual refinement – not one shot. Deduction n Routine inductions – without hypothesis strengthening n Integrate such reasoning with the search Constraint solving n For real-time feature of ES.

FV for ES - Issues n Synthesizing component interfaces reliably. n n Need high level modeling (UML). Consistency of UML diagrams. Synthesize executable description from high level models. Still you might be using other’s components !! n Static verification of unknown components n n Assume guarantee reasoning (Deduction) Extract assumptions/guarantees from interface spec.

FV for ES - Issues n ES software subverts some of the problems of program verification. n Datatypes are often (arrays of) scalar types. Develop specialized provers (with limited theorem proving) n ES software verification should look at both: n n n control intensive, reactive applications Data intensive applications. Reasoning about: n Nested Loops. n Arrays.