79d2f9c99ac0223c68af70c3ce5fce72.ppt
- Количество слайдов: 65

Formal Specification Sets Based on chapter 2 of Formal Specification Using Z David Lightfoot

Problems in the creation of computer systems • There are long-standing problems in the development of computer systems: often they take too much time to produce, cost more than estimated and fail to satisfy the customer. Central to the problem is the fact that errors and inadequacies are more expensive to correct the later in the development process they are discovered. Furthermore, it is extremely difficult to clarify exactly what is required of a very complex system.

Formal Specifications • Formal specifications use mathematical notation to describe in a precise way the properties which an information system must have. • The process of producing a formal specification for an information system has three major steps: • 1) We try to understand what the user requires. • 2) This understanding is then translated into a ‘formal specification’. • 3) We attempt to show that the specification does indeed capture the user requirement. • Given the informal nature of user requirements we may not identify or translate them correctly into our formal specification. Often use our intuition and experience for these two tasks.

Formal Specifications • Since , by their very nature, user requirements must be expressed informally, there are no formal methods for showing that a specification satisfies the user requirements. However, we can convince ourselves that a specification is satisfactory by using the following techniques: • 1) Simply inspect the specification and see that it does meet the requirement. • 2)We can prove that the specification has certain properties which are are to be expected of a solution to the problem. • Both of these activities are much simpler if we have an abstract specification. An abstract specification supplies essential information and is not oriented towards implementation. • These techniques are analogous to how any formalization of a mathematical concept is checked.

Formal Specifications • When constructing a mathematical model of a real world systems there is a certain amount of arbitrariness in the information included in the mathematical formulation. This is just a matter of judgement; inevitably, we are sure to include either too much or too little detail in our specification, and so we will have to go back at some stage and modify it. Mathematics provides no solution to that problem all it can do is ensure that we do include is unambiguous.

Formal Specifications What rather than How • Formal specifications use mathematical notation to describe in a precise way the properties which an information system must have, without unduly constraining the way in which these properties are achieved. They describe what the system must do without saying how it is to be done. This abstraction makes formal specifications useful in the process of developing a computer system, because they allow questions about what the system does to be answered confidently, without the need to disentangle the information from a mass of detailed program code, or to speculate about the meaning of phrases in an imprecisely worded prose description.

Formal Specifications • A formal specification can serve as a single, reliable reference point for 1) those who investigate the customer's needs, 2) those who implement programs to satisfy those needs, 3) those who test the results, and 4) those who write instruction manuals for the system. Because it is independent of the program code, a formal specification of a system can be completed early in its development. Although it might need to be changed as the design team gains in understanding and the perceived needs of the customer evolve, it can be a valuable means of promoting a common understanding among all those concerned with the system.

Z Specifications • The language of Z specifications is grounded in mathematics, and we will give a description of the world in terms of mathematical objects. We describe what objects exist, and how relationships between them may be made into specifications. We will look at the Z language and how it can be used to express specifications, and extend the vocabulary of mathematical objects into a collection of powerful data types.

Z Specifications • The Z method uses the notation of predicate logic to describe abstractly the effect of each operation of our system, in a way that enables us to reason about its behaviour. The other main ingredient in Z is a way of decomposing a specification into small pieces called schemas. By splitting the specification into schemas, we can present it piece by piece. Each piece can be linked with a commentary which explains informally the significance of the formal mathematics.

Z Specifications • In Z, schemas are used to describe both static and dynamic aspects of a system. The static aspects include: • the states it can occupy; • the invariant relationships that are maintained as the system moves from state to state. • The dynamic aspects include: • the operations that are possible; • the relationship between their inputs and outputs; • the changes of state that happen.

Z Issues • Z specifications can appear excessively long in relation to their implementation. • Z needs software tools to keep track of the variables and schemas. • A Z specification is not easily communicated to the user. • Many software engineers do not have the mathematical training to write a Z specification. • The precision Z gives a very high degree of confidence in the fedility of the implementation, that is, that the implementation behaves precisely as the specification.

Z Issues • Verification provides an alternative to testing. To verify an implementation is to demonstrate that it will perform as specified in all cases. This can be done using mathemarical proof. Verification of large systems is not easy. The process of performing a proof is not something that can be completely automated. Although software tools can help, the task seems to be inherently creative in a way that cannot be caputred within a systematic procedure.

Sets • A set is a collection of elements or members. The Z notation uses typed set theory: All the possible values of a set are considered to have something in common, they are said to be the same type. For example sets of persons, sets of numbers. We are not too interested in sets that can contain any sort of element. We will concentrate on typed set theory.

Subsets • Any set is considered to be a subset of its type. Example even numbers are a subset of integers. • A subset is any collection of values from a set.

The Z built in types • The designated Integer symbol is: Z • …, 3, 2, 1, 0, 1, 2, 3… • The designated symbol for Natural numbers including zero is N • 0, 1, 2, 3… • The designated symbol for Natural numbers excluding zero is N 1 • 1, 2, 3. .

Operations on Integers Z • The following operators are defined for the type Integer (Z) and its subsets: • + * div mod

Relations on Integers • The following relational operators are applicable to Integers:

Basic Types • Basic types are called given types. The basic types of a specification are declared without concern for how the elements are represented. Example: • [REGISTRATION] the set of all possible car registrations • [PERSON] the set of all persons • Basic types are written completely in capital letters. It is assumed that the elements are uniquely identifiable. Combined types: • [REGISTRATION, PERSON]

Free Types • There is a need to invent names when creating a formal specification. The rules for constructing such identifiers are similar to those of computer programming languages. Sometimes it is convenient to introduce a type by listing the identifiers of its elements.

Free Types • The general format of a free type is: • free. Type : : = element 1 | element 2 |. . . | elementn • • Examples: RESPONSE : : = yes | no STATUS : : = in. Use | free | on. Hold The symbol : : = means ‘is defined as’

Declaring Variables • Each variable name designating a value must be declared. That means it must be introduced and the type of value it refers must be stated. For example, to introduce a variable chauffeur to the basic type PERSON we write: • chauffeur : PERSON • chauffeur is one of the set of values of PERSON

Example set • Let the set EU be the set of all countries in the European Union. It could have been declared as a basic type, a variable sized set • [EU] the set of all countries in the European Union. • It could also be declared as a fixed size free type: • EU : : = A | B | DK | F | SF | D | GB | GR | IRL | I | L | NL | P | E | S • The variable homeland can refer to one element in the set EU • homeland: EU

Set values • The value of a set can be written by listing its values within braces {}. For example: • benelux={B, NL, L} • Sets are not ordered. There are no duplicates, each element is unique.

The Empty Set Singleton • It is possible to have a set with no values, it is called the empty set and denoted as: 0 or { } • A set that contains only one element is called a singleton set. For example: {IRL} • Note the difference between the set {IRL} and element IRL.

Ranges of Integers • A range of values is denoted as m…n, where m and n are integers, stands for the set of integers m to n inclusive. • If m>n then m. . n = • Examples: • 3. . 5 = { 3, 4, 5} • 2. . 2 = {2} • 3. . 2 =

Set Operators • Set Equivalence • Two values of the same type can be tested to see if they are the same by using the equals sign, as in: • x=y • Two sets are equal if they contain exactly the same elements. For example the two sets below are equal: • {B, NL, L} = {NL, B, L}

Set Operators • Set Non-Equivalence • Two values of the same type can be tested to see if they are not the same by using the not equals sign Two sets are not equal if they do not contain exactly the same elements • {B, NL} {B, NL, L}

Set Operators • The membership operator is written: e • NL e {B, NL, L}it is true; the Netherlands is a Benelux country • General case below: . x S [X] S: PX x: X xe. S X

Set Operators • The non membership operator is written: • IRL {B, NL, L}it is true; Ireland is not a Benelux country [X] S: PX S X x: X . x x S General case

Set Operators • The validity of membership test. • The value to be tested for membership must be an element of the underlying type of the set. For example: • USA e {B, NL, L} • is illegal, since USA is not an element of the type EU.

Set Operators • Size Cardinality: The number of values in a set is called its size, or cardinality, and is signified with the has sign: • #{B, NL, L} = 3 • #{IRL} = 1 • #IRL illegal, IRL is not a set • #0 = 0

Set Operators • Powersets: The powerset of a set is written PS • It is the set of all subsets of S. For example the powerset of the Benelux countries is: P{B, NL, L} = { 0, {B}, {NL}, {B, L}, {NL, L}, {B, NL, L}}

Set Operators: Powersets • When a variable is to be declared to have a type that is a set of elements, the type is the powerset of the type of the elements: • benelux: PEU • This can be read as ‘the variable benelux is a subset of the set of countries EU’ or ‘the variable benelux is a set of EU countries’

Set Operators: Powersets • The size of the powerset of a set is equal to two raised to the power of the size of the set. • #(PS) = 2#s • #{B, NL, L} = 3 • #(P{B, NL, L}) = 8

Set Operators: Set inclusion • The ‘is a sub set of’ operator is: • set 1 z set 2 • The subset operator is true if the first set is included in the second set, that is every element of the first set must be in the second set

Set Operators: Set inclusion The following statements are true: {B, NL} z {B, NL, L} 0 z{B, NL, L} z {B, NL, L} [X] T S S: PX T: PX X Tz. S General case

Set Operators: Set inclusion • The empty set is a subset of every set, including itself. • The empty set is not a member of every set. • The empty set can only be a member of a set of sets. • Elements of set EU that border the Pacific (none) 0 z S is true for all sets S 0 z 0 is true • When checking for singleton inclusion: • ({x} z S) (xe. S)

Set Operators: Union • The union of two sets is the set containing all the elements that are in either the first set or the second set or both. [X] S: PX S T: PX T TUS=TUS X SU 0=S
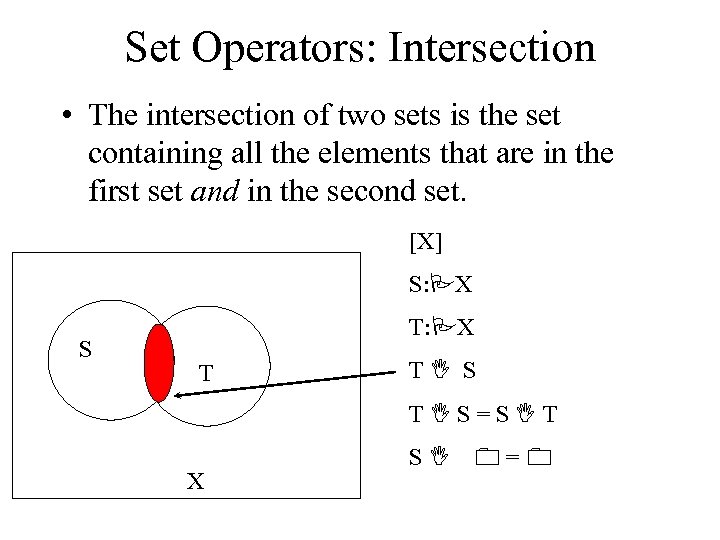
Set Operators: Intersection • The intersection of two sets is the set containing all the elements that are in the first set and in the second set. [X] S: PX S T: PX T TI S TIS=SIT X SI 0=0

Set Operators: Difference • The difference of two sets is the set containing all the elements that are in the first set and are not in the second set. The shaded area is the difference of S and T. [X] S: PX T: PX ST T S S� =S 0 S=0 S T X
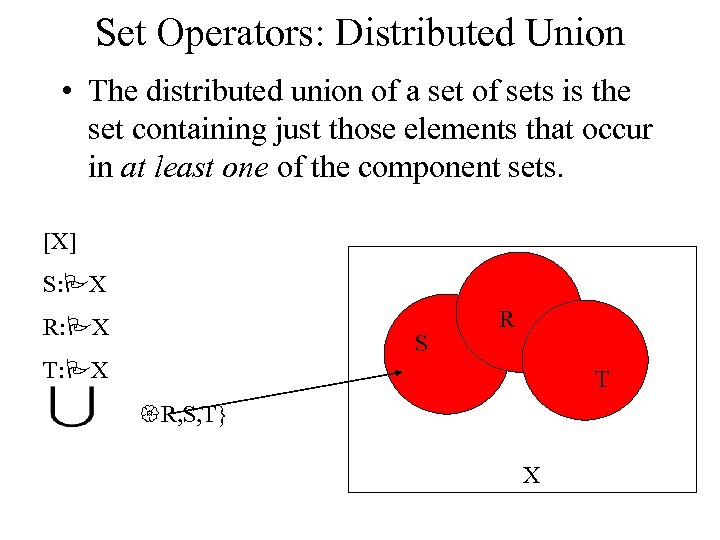
Set Operators: Distributed Union • The distributed union of a set of sets is the set containing just those elements that occur in at least one of the component sets. [X] S: PX R: PX S R T: PX T {R, S, T} X
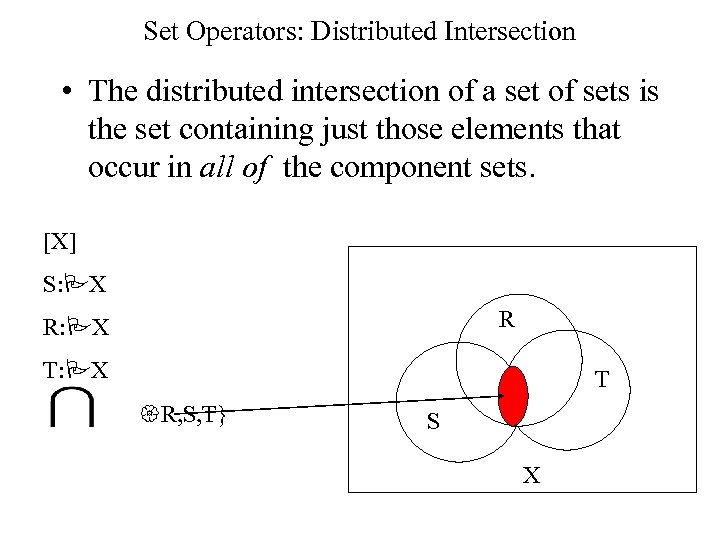
Set Operators: Distributed Intersection • The distributed intersection of a set of sets is the set containing just those elements that occur in all of the component sets. [X] S: PX R R: PX T {R, S, T} S X

Disjoint Sets • Sets that are disjoint have no elements in common; their intersection is the empty set. • For disjoint sets T and S the following expression is true: • T I S = 0.

More than 2 Disjoint Sets • For more that two sets it becomes longer, since every pair must have an empty intersection. For example for sets A, B and C to be disjoint the following must be true: • A I B = 0 and • B I C = 0 and • CIA=0

Disjoint Sets • In Z, we often write: • Example 1 • disjoint<S, T> disjoint<A, B, C> • Example 2 • [PERSON] • male, female: PERSON • disjoint<female, male>

Partition • A sequence of sets is said to partition another larger set if the sets are disjoint and their distributed union is the entire larger set if the sets are disjoint. For example: • if disjoint<A, B, C> and {A, B, C} = T • then <A, B, C> partition T • E. G. <male, female> partition PERSON.

Example • Edward, Fleur, and Gareth have each been given an assignment consisting of 7 questions. Edward has attempted the questions numbered 1, 2, and 4; Fleur has attempted all but questions 5 and 6; Gareth has attempted only those questions with even numbers.

Example • Express these facts using Z typed set theory. • Q 1 Which questions have been attempted by these three students. • Q 2 Which questions were attempted by all three students.
![Example • • Base types [Student] the set of all students (not actually needed) Example • • Base types [Student] the set of all students (not actually needed)](https://present5.com/presentation/79d2f9c99ac0223c68af70c3ce5fce72/image-49.jpg)
Example • • Base types [Student] the set of all students (not actually needed) [Questions] the set of all exam questions Variables edward, fleur gareth: Student edwards. Questions : PQuestions fluers. Questions : PQuestions gareths. Questions: PQuestions

Q 1 Which questions have been attempted by these three students. • edwards. Questions ={ 1, 2, 4} • fluers. Questions ={ 1, 2, 3, 4, 7} • gareths. Questions ={ 2, 4, 6 } Answer: The specification of Query 1 is: {edwards. Questions, fluers. Questions , gareths. Questions} The computed answer for Query 1 is: {1, 2, 3, 4, 6, 7}

Q 1 Which questions have been attempted by all three students. edwards. Questions ={ 1, 2, 4} • • fluers. Questions ={ 1, 2, 3, 4, 7} • gareths. Questions ={ 2, 4, 6 } Answer: The specification of Query 2 is: {edwards. Questions, fluers. Questions , gareths. Questions} The computed answer for Query 2 is: { 2, 4, }

Chapter 2 Exercise 1 • 1. Certain people are registered as users of a computer system. At any given time, some of these users are logged in to the computer. Describe the situation using the concepts of Z covered so far.
![Chapter 2 Solution 1 • [PERSON] the set of all uniquely identifiable persons • Chapter 2 Solution 1 • [PERSON] the set of all uniquely identifiable persons •](https://present5.com/presentation/79d2f9c99ac0223c68af70c3ce5fce72/image-53.jpg)
Chapter 2 Solution 1 • [PERSON] the set of all uniquely identifiable persons • logged. In, users: PPERSON • logged. In z users

Chapter 2 Exercises 2 • 2. Extend your description from Q 1 as follows: • There is a limit (unspecified) to the number of users logged in at any one time.

Chapter 2 SOLUTION 2 • limit: N • #logged. In limit

Chapter 2 Exercises 3 • 3. Extend your description from Q 1 as follows: • All users are either staff users or customers. •

Chapter 2 SOLUTION 3 • staff, customers: PPERSON staff customers = q staff customers = users OR <staff, customer> partition users

Chapter 2 Exercises 4 • Q 4. Express the following statements in Z notation: • All currently logged in users are staff. • There are more customer users than staff users.

Chapter 2 SOLUTION 4 • logged. In z staff • #customers > #staff

Chapter 2 Exercises 5 • Q 5. In a modular university course some modules are acceptable and others are compulsory. Use the names acceptables and compulsories for the sets of modules. Each student studies modules from two fields. The acceptable from the first field are called first. Acc and second. Acc for the second. first. Acc z acceptables second. Acc z acceptables

Chapter 2 Exercises 5 • Write an expression to state that all compulsory modules are also acceptable. • Write an expression that states that there are three compulsory modules. • Write an expression to state that the acceptables for the first field are not the same as the acceptables for the second field. • Write an expression to state that some modules are acceptable for both the first field and the second field.
![Chapter 2 Exercise 5(a) • The base type is [MODULES] the set of all Chapter 2 Exercise 5(a) • The base type is [MODULES] the set of all](https://present5.com/presentation/79d2f9c99ac0223c68af70c3ce5fce72/image-62.jpg)
Chapter 2 Exercise 5(a) • The base type is [MODULES] the set of all possible modules • Variables are • first. Acc, second. Acc, compulsories : PMODULES • Write an expression to state that all compulsory modules are also acceptable. • compulsories z acceptables

Chapter 2 Exercise 5(b) • Write an expression that states that there are three compulsory modules #compulsories = 3

Chapter 2 Exercise 5(c) • Write an expression to state that the acceptables for the first field are not the same as the acceptables for the second field first. Acc second. Acc

Chapter 2 Exercise 5(d) • Write an expression to state that some modules are acceptable for both the first field and the second field. first. Acc second. Acc
79d2f9c99ac0223c68af70c3ce5fce72.ppt