Formal Software Verification Christelle Scharff http www csis

Formal Software Verification Christelle Scharff http: //www. csis. pace. edu/~scharff May 2004 DPS, Pace University

References Use of the slides of Dr. Clark Barrett (with permission) ITR NSF Little Engines of Proof Stanford Research Institute with and Clarkson University, 2003 Automated Deduction with Constraints and Simplification in Equatio Theories, Christelle Scharff, Ph. D, 1999 ICS (I can Solve or Integrated Canonizer and Harald Ruess, Solver), 2002 Abstract Congruence Closure, Leo Bachmair, Ashish Laurent Tiwari and , Vigneron, 2003 Unsound Theorem Proving, Christopher Lynch, 2004 Direct Combination of Completion and Congruence Closure, Christelle Scharff and Leo Bachmair, 2002 and 2004 On prototyping Deduction with Constraints and Simplification in a Rewriting Language , Christelle Scharff, 2004

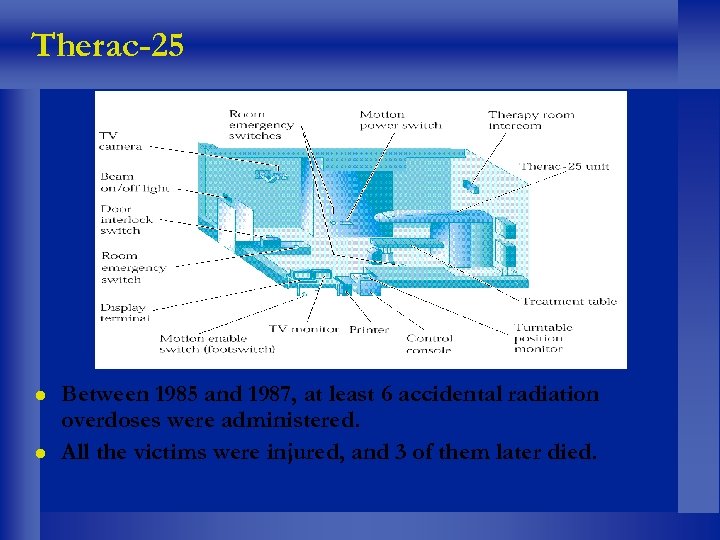Therac-25 Between 1985 and 1987, at least 6 accidental radiation overdoses were administered. All the victims were injured, and 3 of them later died.

Ariane 5 Rocket On June 4, 1996, an unmanned Ariane 5 rocket launched by the European Space Agency exploded just 40 seconds after its lift-off. Value of rocket and cargo: $500 million

Blackout In August, 2003, the largest blackout in our country’s history occurred. Estimated cost to New York City alone: $1. 1 billion.

What do these events have in common? Caused by Software Bugs! Each of the overdoses from the Therac-25 was the result of a bug in the controlling software. The Ariane 5 explosion was the result of an unsafe floating point to integer conversion in the rocket’s software system. A software bug caused an alarm system failure at First. Energy in Akron, Ohio. An early response to those alarms would likely have prevented the blackout.

More horror stories Software Reliability: Principles and Practice, p 25, by G. J. Myers Appolo 8 spacecraft erased part of the computer's memory. Eighteen errors were detected during the 10 -day flight of Apollo 14. An error in a single FORTRAN statement resulted in the loss of the first American probe to Venus.

Why must we suffer so? Engineers are supposed to be good at building things. When we build a building, we don’t expect it to crumble and have to be rebuilt twice a week. Why don’t we have software engineers who build better software? It’s not all Microsoft’s fault. Software may be the most complex thing ever created. Getting software right is a very, very difficult task. Existing engineering techniques are inadequate.

Outline What is Formal Verification? Model Checking Theorem Proving Systems and Tools Demonstrations (Eclipse, ICS, GACC) Conclusions and Future Work

What is Formal Verification? “[Formal] software verification … has been the Holy Grail of computer science for many decades” – Bill Gates Formal Verification (Proving) versus Validation (Testing) Create a mathematical model of the system An inaccurate model can introduce or mask bugs. Fortunately, this can often be done automatically. Specify formally what the properties of the system should be Prove that the model has the desired properties Much better than any testing method Covers all possible cases This is the hard part There a variety of tools and techniques

Proof techniques Model Checking Typically relies on low-level Boolean logic Proof is automatic Does not always scale to large systems Theorem Proving Typically uses more expressive logic (higher order logic) Proof is automatic in first order logic Proof is manually directed (in higher order logic) Unlimited scalability Advanced techniques combine elements of both

Outline What is Formal Verification? Model Checking Theorem Proving Systems and Tools Demonstrations (ICS, GACC, Eclipse) Conclusions and Future Work

Formal Models Typically, a formal model is a graph in which each vertex represents a stateof the program, and each edge represents a transition from one state to another. Consider this simple program: The states of this program are all possible pairs of the variables x and y. Fortunately, we can restrict our attention to the reachable states. int x, y; x = 0; y = 0; while (x < 4) { x++; y = y + x; }

Reachable States and Checking Properties We can check a property by verifying that it is truein every reachable state. If the property is false then there is a bug. , x≥ 0 0, 0 Initial State x≥y int x, y; x = 0; 1, 0 1, 1 y = 0; while (x < 4) { x++; 2, 1 2, 3 y = y + x; } 3, 3 3, 6 Final State

Outline What is Formal Verification? Model Checking Theorem Proving Systems and Tools Demonstrations (Eclipse, ICS, GACC) Conclusions and Future Work

Theorem Proving Theorem proving relies on human ingenuity and symbolic manipulations to prove that a program satisfies some properties. Typically, proving a single property about a program will require proving many other properties as well. Theorem Prover = Software based on Inference Rules + Strategy Inference Rules: How to deduce new data? How to remove data? Strategy: How to apply the inference rules?

Theorem Proving What are the properties of theorem provers? Soundness (Mandatory Property) Do not prove that True = False Prove only true formulae Completeness (Optional Property) If a formula is true, it can be proved. Termination (Undecidable Property) Does the application of the rules with the strategy terminate?

Theorem Proving One approach is to annotate the program with theorems to be proved (e. g. preconditions , post-conditions , invariants, assertions ), and then prove that each theorem really does hold. Hoare Logic Consider a simple program: Suppose we wish to prove that, if x = y before the execution of this program, then at the end of its execution, x = y. We can annotate the beginning and the end of the program with these properties. [x=y] x=x+1 y=y+1 [x=y]

Theorem Proving What is the condition that will guarantee that x = y after executing y = y + 1 ? To find out, propagate the assertions upward through the program. We imagine trying to prove x = y using primed variables to represent the values after the execution of y = y + 1, and unprimed variables for the values before it: (? ) y’ = y + 1 x’ = x x’ = y’ (? ) x = y + 1 [x=y] x=x+1 [x = y + 1] y=y+1 [x=y]

Theorem Proving What is the condition that will guarantee that x = y + 1 after executing x = x + 1 ? To find out, we imagine trying to prove x = y + 1 using primed variables to represent the values after the execution of x = x + 1, and unprimed variables for the values before it: (? ) x’ = x + 1 y’ = y x’ = y’ + 1 (? ) x + 1 = y + 1 [x=y] [x + 1 = y + 1] x=x+1 [x = y + 1] y=y+1 [x=y]

Theorem Proving We prove that the program is correct by proving that: x = y implies x + 1 = y + 1 using a theorem prover. [x=y] [x + 1 = y + 1] x=x+1 [x = y + 1] y=y+1 [x=y]

Outline What is Formal Verification? Model Checking Theorem Proving Systems and Tools Demonstrations (Eclipse, ICS, GACC) Conclusions and Future Work

Systems and Tools Model checkers SMV SPIN Theorem provers Little Engines of proof Automated domain-specific theorem provers (uninterpreted functions, linear arithmetic, arrays, bitvectors. . . ) ICS, CVC lite GACC (Graph-based Abstract Congruence Closure ) Other Engines of proof PVS, Isabelle, HOL Ba. CCS (Basic Completion with Constraint and Simplificati )

Microsoft SLAM Clever combination of model checking and automated theorem proving An abstract program is created in which all conditions are replaced with Boolean variables Resulting Boolean program is model checked If model checking fails, the potential error path is checked in the original program using an automated theorem prover Successfully used to find bugs in Windows drivers. …reducing the frequency of “Blue Screens of Death”!

Outline What is Formal Verification? Model Checking Theorem Proving Systems and Tools Demonstrations (Eclipse, ICS, GACC) Conclusions and Future Work

Eclipse is an open source IDE developed by IBM Eclipse is a “kind of universal tool platform – an open extensible IDE for anything and nothing in particular. ” Eclipse can be used to create applications as diverse as web sites, java programs, C++ programs. . . An extension to Eclipse is called a plugin. http: //www. eclipse. org

Demo of ICS (I can solve Integrated or Canonizer and Solver ) Developed at SRI. http: //www. ics. com Decides formulae in a useful combination of theories (non interpreted formulae, bitvectors, reals, arrays…) & means AND, | means OR, and ~ means NOT. Example 1: Ics> sat x = 2 & x = 3; Answer: unsat Example 2: Ics> sat [x = 2 | x = 3] & x < 3; Answer: sat, model [x = 2; 3 + - 1 * x > 0]

Demo of ICS (I can solve Integrated or Canonizer and Solver ) If we want to prove: p q, then we use refutational theorem proving. In fact, we assume that the hypotheses are true, and that the conclusion is false. Then, if p q is true, we will derive a contradiction (unsat). Otherwise, the resulting model provides us with a counter-example. Example 3: If x = 2 and y = 4, then x + y = 6 ? ? ics> sat x = 2 & y = 4 & ~ x + y = 6; Answer: unsat If x = 2 or x = 5, then x < 4 ? ? ics> sat [x = 2 | x = 5] & ~ x < 4; Answer: sat, model [-4 + x >= 0; x = 5]

Demo of GACC (Graph-based Abstract Congruence Closure ) Congruence Closure is a method for deciding ground equalities. Example: From f(a) = b and a = c, we can deduce f(c) =b. The system GACC implements a new algorithm of congruence closure based on the use of graph with labeled vertices and edges. GACC was implemented by Eugene Kipnis from Pace University under my supervision, and is available for online experimentation at: http: //www. csis. pace. edu/~scharff/SOFTWARE

Outline What is Formal Verification? Model Checking Theorem Proving Systems and Tools Demonstrations (Eclipse, ICS, GACC) Conclusions and Future Work

Conclusions Formal Software Verification is starting to become practical Still lots of work to be done How can it make you a better programmer? Document your code with the properties and invariants that you think should be true When you modify code, convince yourself that you are not breaking any invariants Hopefully, someday software will be as safe and reliable as the other objects built by engineers!

Environment CAFME Center create by Dr. Skevoulis CS 851: Software Validation and Verification New course offered in the Fall 2004 Part of the degree in Software Design and Development Validation = Testing Verification = Proving ITR NSF Grant “Little Engines of Proof” with Stanford Research Institute, and Clarkson University

Future Work 1: Eclipse Plugin A java program is annotated with assertions to be proved Assertions are written in the ICS syntax Some assertions are computed. Assertions are propagated up through the program line by line ICS will be called from the java program, and the assertions will be checked Parts of the program will be proved correct, or bugs will be discovered

Future Work 2: Strategies Rewriting languages (e. g. ELAN, MAUDE, OBJ, ASF+SDF) are very expressive, and very convenient to prototype theorem provers Rewriting languages share many features with functional programming languages (no side-effect, use of recursion, pattern matching…), but they are based on rewriting instead of lambda calculus Can we develop a Java API that would be used to prototype theorem provers? Can we define the strategy on the rules in an XML document?

Future Work 3: Correctness of Abstract Congruence Closure Abstract congruence closure is a framework that defines a set of inference rules and different strategies for congruence closure. These strategies include strategies that simulate Nelson-Oppen, Shostak and Downey-Sethi-Tarjan algorithms The rules and the strategies can be implemented easily using a rewriting language such as ELAN This implementation would be a formal framework to prove the correctness of the abstract congruence closure algorithm, and, besides, would permit intensive benchmarking on criteria to be defined

Future Work 4: Unsound Theorem Proving Many problems given to a theorem prover will be false conjectures. It is important to be able to find quickly bugs in programs. An inference system for unsound theorem proving (or theorem (dis)proving) has been defined by Christopher Lynch. The theorem (dis)prover can be prototyped in a rewriting language such as ELAN. This framework could be used to show the correctness of the procedure, and benchmark the method on criteria to be defined