ddf3633b8891d9f70dbf635a39c4b8ab.ppt
- Количество слайдов: 42

Formal Methods Quick Tutorial Ricky W. Butler Oct 22, 2003 http: //shemesh. larc. nasa. gov/fm 1

Outline • Motivation (3 minutes) • Formal Methods by way of example — Theorem Proving (12 minutes) — Model Checking state machines (12 minutes) • A Few More Thoughts (3 minutes) 2

“There are no stupid questions” 3

Motivation Say, I think I see where we went off. Isn’t eight times seven fifty-six? 4

Software Underpins Everything In Aviation • Increased Capabilities – Almost any breakthrough in any field will depend on advanced computer systems – And software is where most of the complexity goes • Software Costs Dominate – Development costs (More than half of the non-recurring development of the Boeing 777) – Integration (only way of testing it is all-up simulation) – Certification (based on process, not product) • Major Safety Concerns – – Reliability Correctness Man-machine interaction Certification (dealing with hardware failures) (no faults in its own design) (issue in majority of recent crashes) (complexity forces FAA to rely on DERs) 5
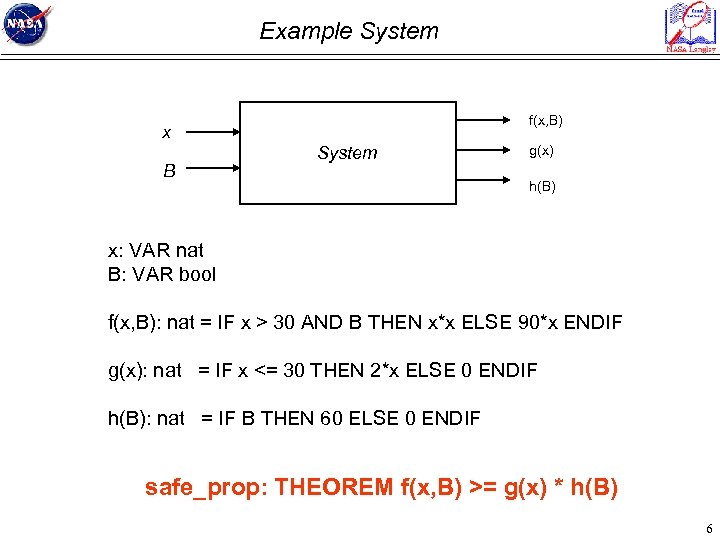
Example System f(x, B) x B System g(x) h(B) x: VAR nat B: VAR bool f(x, B): nat = IF x > 30 AND B THEN x*x ELSE 90*x ENDIF g(x): nat = IF x <= 30 THEN 2*x ELSE 0 ENDIF h(B): nat = IF B THEN 60 ELSE 0 ENDIF safe_prop: THEOREM f(x, B) >= g(x) * h(B) 6

Design Verification In the beginning, there was Simulation: • Build a model • Feed IT inputs • Analyze results 7

Verification by Simulation x: VAR nat B: VAR bool f(x, B): nat = IF x > 30 AND B THEN x*x ELSE 90*x ENDIF g(x): nat = IF x <= 30 THEN 2*x ELSE 0 ENDIF h(B): nat = IF B THEN 60 ELSE 0 ENDIF safe_prop: THEOREM f(x, B) >= g(x) * h(B) x B -----0 T 10 F 50 T 30 F 30 T f g h --------------0 0 60 1200 20 0 2500 0 60 3600 60 0 2700 60 60 safe_prop -------TRUE FALSE 8
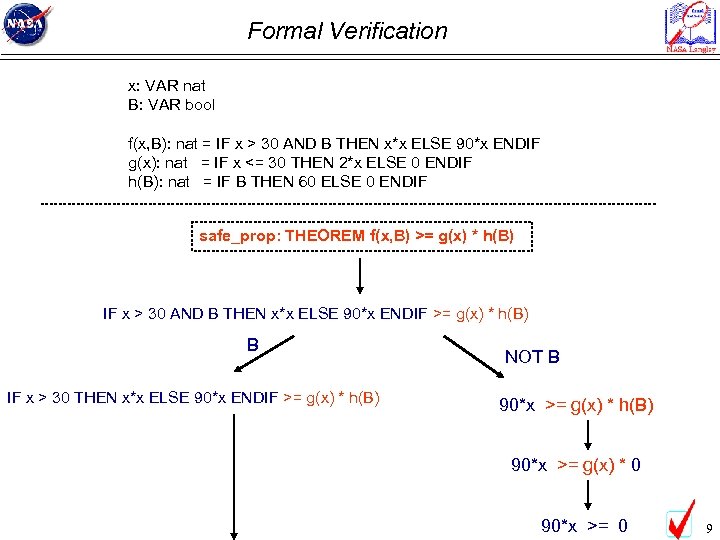
Formal Verification x: VAR nat B: VAR bool f(x, B): nat = IF x > 30 AND B THEN x*x ELSE 90*x ENDIF g(x): nat = IF x <= 30 THEN 2*x ELSE 0 ENDIF h(B): nat = IF B THEN 60 ELSE 0 ENDIF safe_prop: THEOREM f(x, B) >= g(x) * h(B) IF x > 30 AND B THEN x*x ELSE 90*x ENDIF >= g(x) * h(B) B IF x > 30 THEN x*x ELSE 90*x ENDIF >= g(x) * h(B) NOT B 90*x >= g(x) * h(B) 90*x >= g(x) * 0 90*x >= 0 9
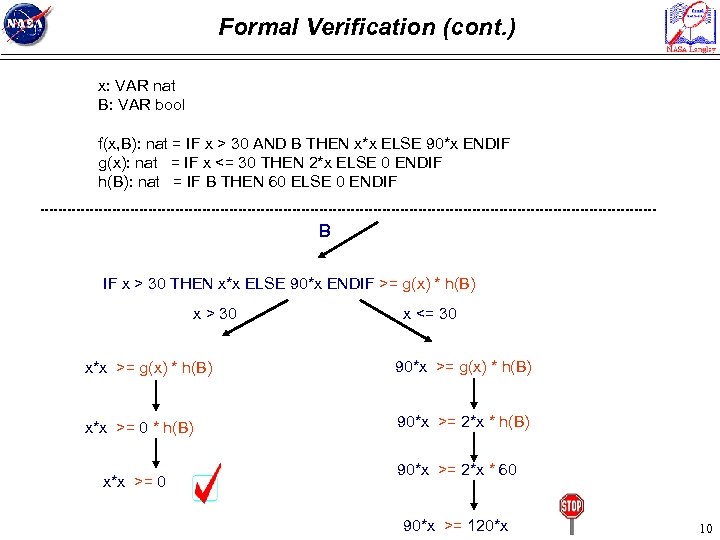
Formal Verification (cont. ) x: VAR nat B: VAR bool f(x, B): nat = IF x > 30 AND B THEN x*x ELSE 90*x ENDIF g(x): nat = IF x <= 30 THEN 2*x ELSE 0 ENDIF h(B): nat = IF B THEN 60 ELSE 0 ENDIF B IF x > 30 THEN x*x ELSE 90*x ENDIF >= g(x) * h(B) x > 30 x <= 30 x*x >= g(x) * h(B) 90*x >= g(x) * h(B) x*x >= 0 * h(B) 90*x >= 2*x * h(B) x*x >= 0 90*x >= 2*x * 60 90*x >= 120*x 10

Using a “Mechanical” Proof Checker (PVS) PVS SPECIFICATION OUTPUT FROM PVS THEOREM PROVER safe_prop : demo_incorrect: THEORY BEGIN x: VAR nat B: VAR bool f(x, B): nat = IF x > 30 AND B THEN x*x ELSE 90*x ENDIF g(x): nat = IF x <= 30 THEN 2*x ELSE 0 ENDIF h(B): nat = IF B THEN 60 ELSE 0 ENDIF safe_prop: THEOREM f(x, B) >= g(x) * h(B) END demo_incorrect |------{1} FORALL (B: bool, x: nat): f(x, B) >= g(x) * h(B) Rule? (grind) f rewrites f(x, B) to IF x > 30 AND B THEN x * x ELSE 90 * x ENDIF g rewrites g(x) to IF x <= 30 THEN 2 * x ELSE 0 ENDIF h rewrites h(B) to IF B THEN 60 ELSE 0 ENDIF Trying repeated skolemization, instantiation, and if-lifting, this simplifies to: safe_prop : {-1} x!1 >= 0 {-2} B!1 |------{1} x!1 > 30 {2} 90 * x!1 >= 120 * x!1 Rule? 11

Using a “Mechanical” Proof Checker (PVS) CORRECTED PVS SPECIFICATION OUTPUT FROM PVS THEOREM PROVER safe_prop : demo_correct: THEORY BEGIN x: VAR nat B: VAR bool f(x, B): nat = IF x > 30 AND B THEN x*x ELSE 90*x ENDIF g(x): nat = IF x <= 30 THEN 2*x ELSE 0 ENDIF h(B): nat = IF B THEN 40 ELSE 0 ENDIF safe_prop: LEMMA f(x, B) >= g(x) * h(B) |------{1} FORALL (B: bool, x: nat): f(x, B) >= g(x) * h(B) Rule? (grind) f rewrites f(x, B) to IF x > 30 AND B THEN x * x ELSE 90 * x ENDIF g rewrites g(x) to IF x <= 30 THEN 2 * x ELSE 0 ENDIF h rewrites h(B) to IF B THEN 40 ELSE 0 ENDIF Trying repeated skolemization, instantiation, and if-lifting, Q. E. D. Run time = 0. 35 secs. Real time = 3. 33 secs. END demo_correct 12

The Key Difference • Simulation/Testing only explores a small part of the state space • Formal Verification explores the entire state space The only way you can assure yourself that there are no safety-relevant bugs hidden in some dark corner of your software is to explore the entire state space. 13
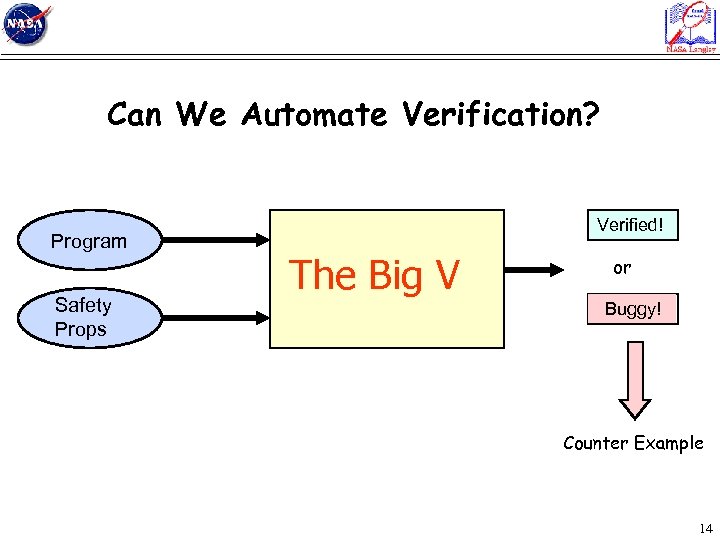
Can We Automate Verification? Program Safety Props Verified! The Big V or Buggy! Counter Example 14

Kurt Goedel (1906 -1978) Answer: NO! 15

Why Can’t We Automate Verification? • Algebra (in general) is undecidable (i. e. There is no terminating algorithm that can determine whether a formula is true) But some sub-theories are decidable (e. g. Presburger arithmetic): develop automated decision procedures • While loops in a program lead to induction proofs (Discovery of the induction invariant involves creativity: n: P(n) requires P(n) Q 1(n) … Qj(n)) • Modeling the environment that the program interacts with often involves continuous mathematics (e. g. calculus, trig) hybrid models • Finite-state models can be automatically analyzed via model-checking (execution times can be exorbitant) 16

Proof Checkers But we do use Proof Checkers! (aka Theorem Provers) -- because we make too many mistakes Why then do you call it a “theorem prover” if it can only check? Because it does help, it just can’t do the whole job. 17

State Machine Analysis State = (x: nat, y: nat) Events = {ex, ey, em , es} 18
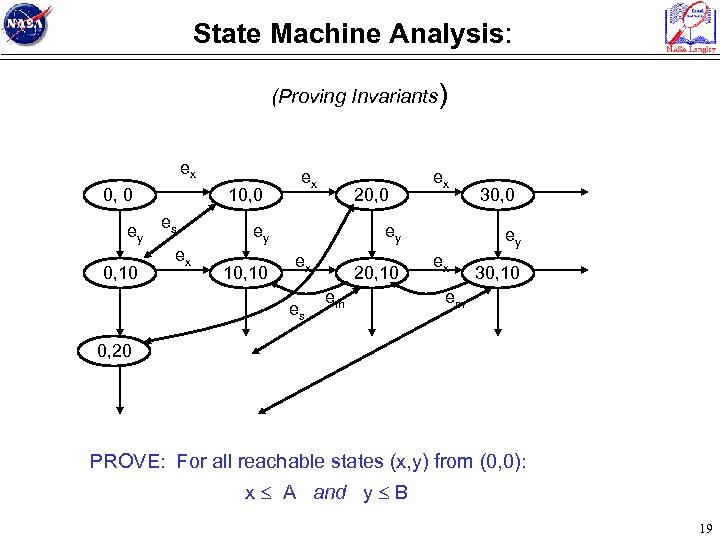
State Machine Analysis: (Proving Invariants) ex 0, 0 ey 0, 10 10, 0 es ex ex 20, 0 ey 10, 10 ex ey ex es 20, 10 em 30, 0 ey ex 30, 10 em 0, 20 PROVE: For all reachable states (x, y) from (0, 0): x A and y B 19

State Machine Analysis: (Proving Invariants) • Theorem proving – deduction – human directed • Model checking – exhaustive search – automatic – state space must be finite 20
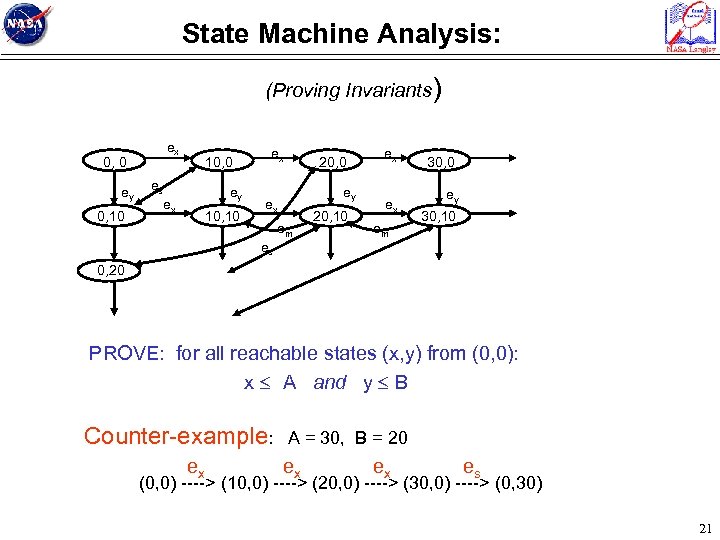
State Machine Analysis: (Proving Invariants) ex 0, 0 ey 0, 10 10, 0 es ey ex 10, 10 ex 20, 0 ey ex em 20, 10 ex ex em 30, 0 ey 30, 10 es 0, 20 PROVE: for all reachable states (x, y) from (0, 0): x A and y B Counter-example: ex A = 30, B = 20 ex ex es (0, 0) ----> (10, 0) ----> (20, 0) ----> (30, 0) ----> (0, 30) 21

State Machine Analysis: (Proving Invariants) INVARIANT: For all reachable states (x, y) from (0, 0) that x max(A, B) and y max(A, B) Proof Approach: Assume invariant holds in current state. Show each transition preserves the invariant. By induction true for all reachable states. 22

SMV Version of State Machine MODULE main VAR x : 0. . 50; y : 0. . 50; event: {ex, ey, em}; ASSIGN init(x) : = 0; init(y) : = 0; next(x) : = case event = ex & x <= AA - 10 : x + 10; event = ey & y <= BB - 10 : x; event = em & x > y & y > 0 : x - y; event = em & y > x & x > 0 : x; 1 : y; esac; next(y) : = case event = ex & x <= AA - 10 : y; event = ey & y <= BB - 10 : y + 10; event = em & x > y & y > 0 : y; event = em & y > x & x > 0 : y - x; 1 : x; esac; 23
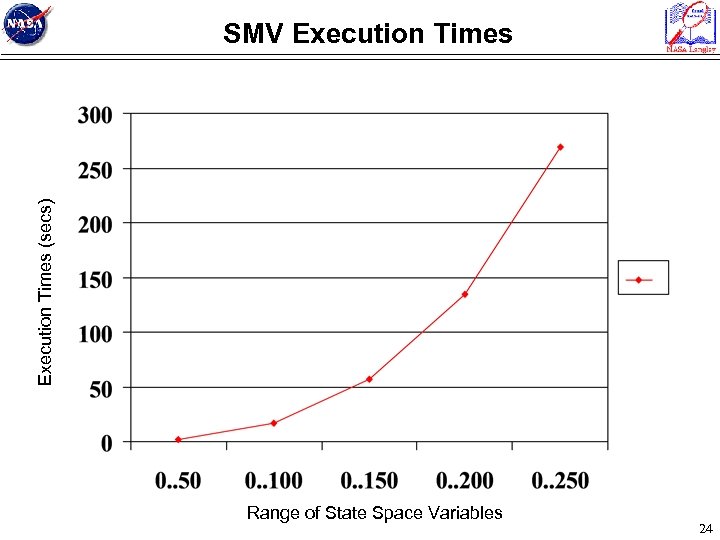
Execution Times (secs) SMV Execution Times Range of State Space Variables 24

25

Output From SMV Model Checker DEFINE AA : = 40; BB : = 50; invariant_1 : = AG (x <= AA & y <= BB); invariant_2 : = AG (x <= max_AB & y <= max_AB); -- specification invariant_1 is false -- as demonstrated by the following execution sequence state 1. 1: x=0 y=0 event = em state 1. 2: event = ey state 1. 3: y = 10 state 1. 4: y = 20 state 1. 5: y = 30 -- specification invariant_2 is true state 1. 6: y = 40 state 1. 7: y = 50 event = em state 1. 8: x = 50 y=0 26

Different perspectives on the Joys of Theorem Proving Ms. Miller, tell the verification team I will be a little late with that proof. Just two more lemmas and the proof of the KB 3 D CD&R algorithm will be complete! 27
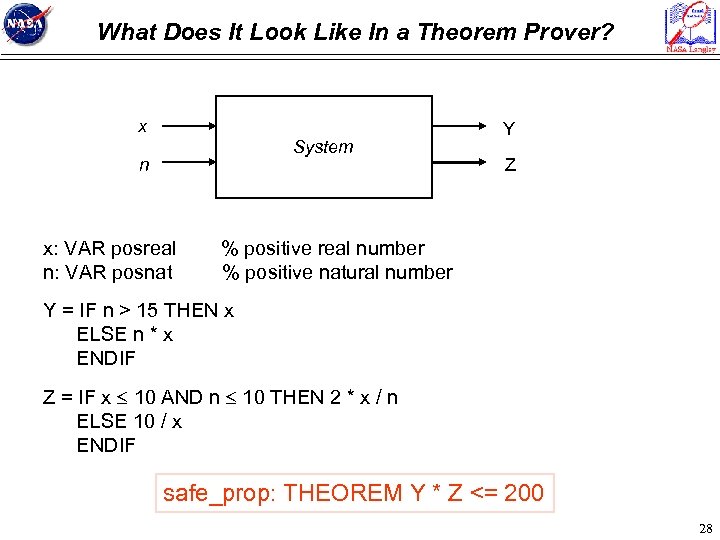
What Does It Look Like In a Theorem Prover? x System n x: VAR posreal n: VAR posnat Y Z % positive real number % positive natural number Y = IF n > 15 THEN x ELSE n * x ENDIF Z = IF x 10 AND n 10 THEN 2 * x / n ELSE 10 / x ENDIF safe_prop: THEOREM Y * Z <= 200 28
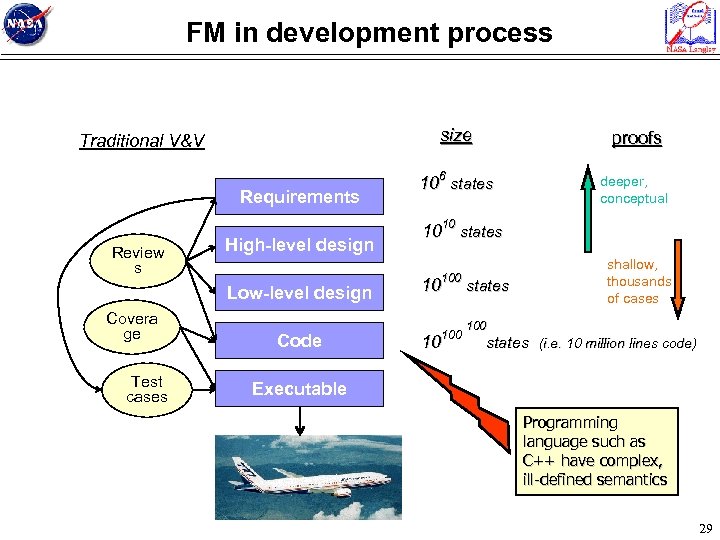
FM in development process size Traditional V&V Requirements Review s High-level design Low-level design Covera ge Test cases Code proofs 106 states deeper, conceptual 1010 states 100 10 states shallow, thousands of cases 100 states (i. e. 10 million lines code) Executable Programming language such as C++ have complex, ill-defined semantics 29
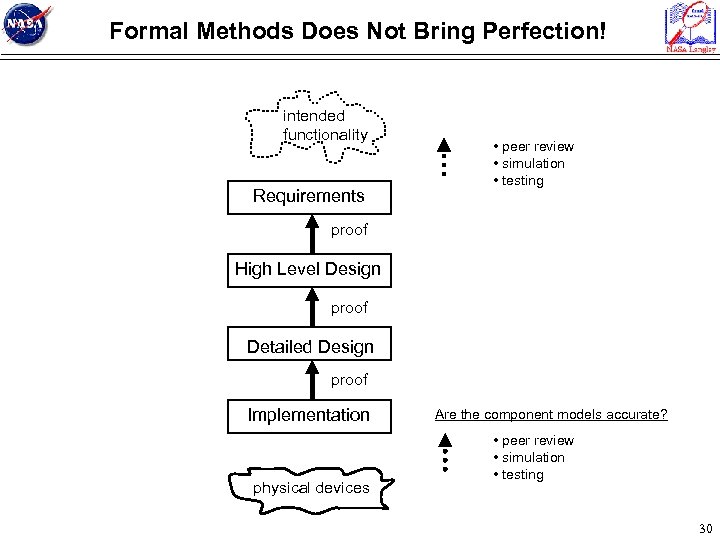
Formal Methods Does Not Bring Perfection! intended functionality Requirements • peer review • simulation • testing proof High Level Design proof Detailed Design proof Implementation physical devices Are the component models accurate? • peer review • simulation • testing 30

Warning: some of our team members are a little sensitive You guys are both my witnesses…He insinuated that ZFC set theory is superior to type theory! 31

The Research Challenge • Formal Methods are not a silver bullet: – Must be applied early in life cycle---not a band aid – Involves a significant learning curve – Each new application requires the development of new models and analysis techniques – Cost of using formal methods still high for some applications. • The software engineering community is dominated by the process management viewpoint (i. e. , that careful management of software development process is the key to quality) • Historically, disasters must occur before major changes are made. 32

EXTRA SLIDES 33

What Does It Look Like In a Theorem Prover? sys_lem: {-1} Y = IF n > 15 THEN x ELSE n * x ENDIF {-2} Z = IF x <= 10 AND n <= 10 THEN 2 * x / n ELSE 10 / x ENDIF |------[1] Y * Z <= 200 Rule? (case "n > 15") Case splitting on n > 15, this yields 2 subgoals 34

What Does It Look Like In a Theorem Prover? sys_lem. 1 {-1} n > 15 [-2] Y = IF n > 15 THEN x ELSE n * x ENDIF [-3] Z = IF x <= 10 AND n <= 10 THEN 2 * x / n ELSE 10 / x ENDIF |------[1] Y * Z <= 200 Rule? (assert) Simplifying, rewriting, and recording with decision procedures, This completes the proof of sys_lem. 1 What Happened? Well, assuming n > 15 we have: Y=x Z = 10 / x 35

What Does It Look Like In a Theorem Prover? sys_lem. 2 give us the other subgoal [-1] Y = IF n > 15 THEN x ELSE n * x ENDIF [-2] Z = IF x <= 10 AND n <= 10 THEN 2 * x / n ELSE 10 / x ENDIF {-3} n <= 15 |------[1] Y * Z <= 200 Rule? (assert) Simplifying, rewriting, and recording with decision procedures, 36

What Does It Look Like In a Theorem Prover? sys_lem. 2 {-1} Y = n * x [-2] Z = IF x <= 10 AND n <= 10 THEN 2 * x / n ELSE 10 / x ENDIF [-3] n <=15 |------[1] Y * Z <= 200 Rule? (replace -1) (hide -1) sys_lem. 2 [-1] Z = IF x <= 10 AND n <= 10 THEN 2 * x / n ELSE 10 / x ENDIF [-2] n <=15 |------[1] n*x* Z <= 200 37

What Does It Look Like In a Theorem Prover? Rule? (case "x <= 10 AND n <= 10") Case splitting on x <= 10 AND n <= 10, this yields 2 subgoals sys_lem. 2. 1 {-1} x <= 10 AND n <= 10 [-2] Z = IF x <= 10 AND n <= 10 THEN 2 * x / n ELSE 10 / x ENDIF [-3] n <=15 |------[1] n * x * Z <= 200 Rule? (replace -1) Replacing using formula -1, this simplifies to 38

What Does It Look Like In a Theorem Prover? sys_lem. 2. 1 {-1} Z = 2 * x / n [-2] n <= 10 [-3] x <= 10 |------[1] n * x * Z <= 200 Rule? (replace -1) (hide -1) [-1] n <= 10 [-2] x <= 10 |------{1} n * x * (2 * x / n) <= 200 Rule? (assert) hit it with the hammer 39
![What Does It Look Like In a Theorem Prover? sys_lem. 2. 1 [-1] n What Does It Look Like In a Theorem Prover? sys_lem. 2. 1 [-1] n](https://present5.com/presentation/ddf3633b8891d9f70dbf635a39c4b8ab/image-40.jpg)
What Does It Look Like In a Theorem Prover? sys_lem. 2. 1 [-1] n <= 15 [-2] x <= 10 |------{1} n * x * (2 * x / n) <= 200 But nothing happens! Rule? (mult-ineq -2 -2) {-1} x * x <= 10 * 10 [-2] n <= 15 [-3] x <= 10 |------{1} n * x * (2 * x / n) <= 200 hit it with the hammer again Rule? (assert) Simplifying, rewriting, and recording with decision procedures, This completes the proof of sys_lem. 2. 1. 40
![What Does It Look Like In a Theorem Prover? [-1] Z = IF x What Does It Look Like In a Theorem Prover? [-1] Z = IF x](https://present5.com/presentation/ddf3633b8891d9f70dbf635a39c4b8ab/image-41.jpg)
What Does It Look Like In a Theorem Prover? [-1] Z = IF x <= 10 AND n <= 10 THEN 2 * x / n ELSE 10 / x ENDIF {-2} NOT (x <= 10 AND n <= 10) {-3} n <= 15 |------[1] n * x * Z <= 200 Rule? (replace -1) (hide -1) {-1} x >10 OR n > 10 {-2} n <= 15 |------[1] n * x * 10 / x <= 200 Rule? (assert) This completes the proof of sys_lem 2. 2. This completes the proof of sys_lem. 2. Q. E. D. 41
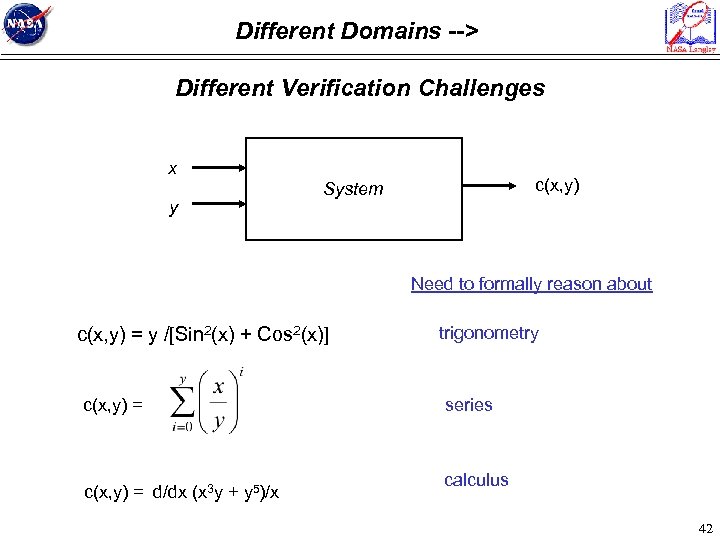
Different Domains --> Different Verification Challenges x y c(x, y) System Need to formally reason about c(x, y) = y /[Sin 2(x) + Cos 2(x)] c(x, y) = d/dx (x 3 y + y 5)/x trigonometry series calculus 42
ddf3633b8891d9f70dbf635a39c4b8ab.ppt