Forces in Magnetic Field • • • Force on Current in Magnetic Field Forces between Currents Force on Moving Charges in Magnetic Field Magnetic Flux. Gauss’s Theorem Work Done on Displacement of a Wire with Current in Magnetic Field • Laws of Magnetic Circuits
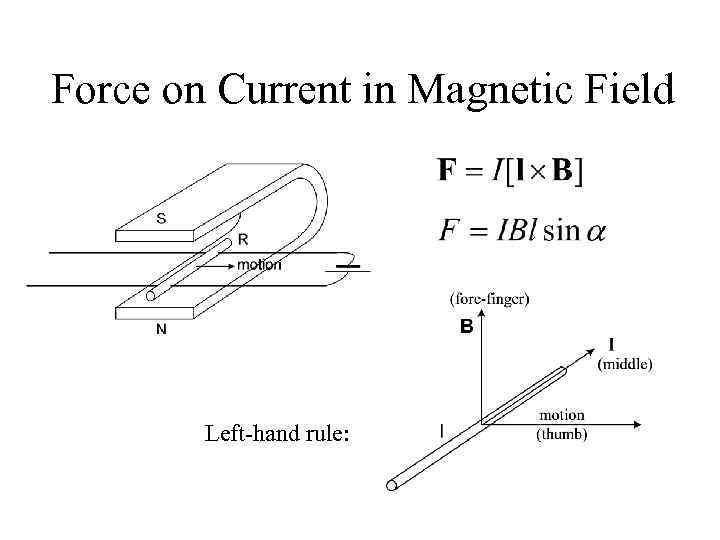Force on Current in Magnetic Field Left-hand rule:
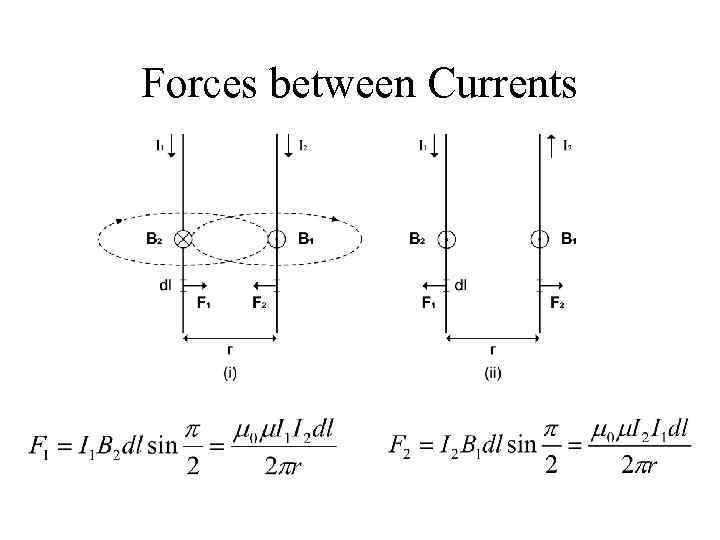Forces between Currents
Force on Moving Charges in Magnetic Field 1. Charge moves at a right angle to a magnetic field The direction of the force is given by the left-hand rule.
Charge moves at a right angle to a magnetic field A charged particle moving in a plane perpendicular to a magnetic field will move in a circular orbit with the magnetic force playing the role of centripetal force. Equating the centripetal force with the magnetic force and solving for R, the radius of the circular path, we get R = m v / q B
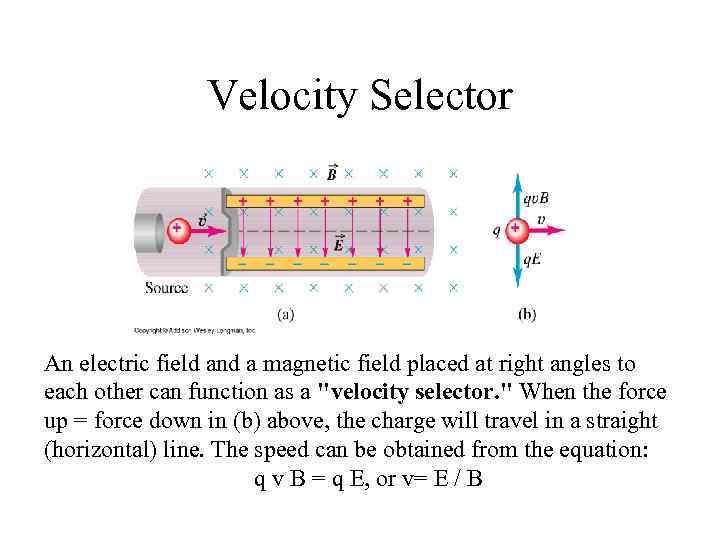Velocity Selector An electric field and a magnetic field placed at right angles to each other can function as a "velocity selector. " When the force up = force down in (b) above, the charge will travel in a straight (horizontal) line. The speed can be obtained from the equation: q v B = q E, or v= E / B
Mass Spectrometer Charged particles leaving a velocity selector (with a known velocity) can be inserted into a chamber with a magnetic field as shown. In the circular orbit equation above R = mv / q B we can substitute v = E / B to get R = m E / q B^2 from which we can solve for m / v, the mass-to-charge ratio. Knowing the charge (ionized state) and the measured radius we can find the mass of he particle.
Force on Moving Charges in Magnetic Field (cont. ) Force = 0
Earth’s surface is protected from dangerous cosmic radiation Electrons and protons are trapped by the terrestrial magnetic field, forming the Van Allen radiation belts, which loop above Earth’s atmosphere between magnetic poles. The trapped particles bounce back and forth, from end to end of the ‘magnetic bottle’, within a few seconds.
Polar Aurora When a large solar flare shoots additional energetic electrons and protons into the radiation belts, an electric field is produced in the region where electrons normally reflect. This field eliminates the reflection and drives electrons down into the atmosphere, where they collide with atoms and molecules of air, causing them to emit light. Birkeland’s experiment:
Torque on a Coil in a Uniform Magnetic Field dc motors operational principle: the couple produces a torque and the coil turns.
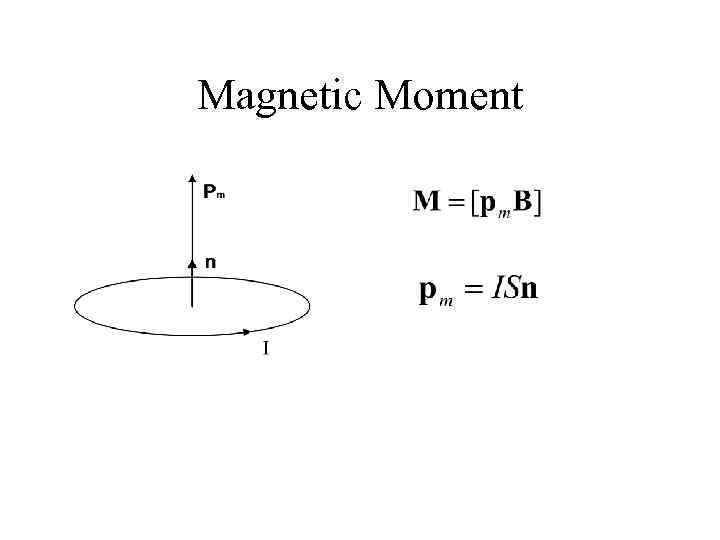Magnetic Moment
Magnetic Flux. Gauss’s Theorem The magnetic flux through any closed surface is zero. Magnetic flux density is the amount of magnetic flux per unit area of a section, perpendicular to the direction of flux.
Work Done on Displacement of a Wire with Current in Magnetic Field Work done by Ampere’s force on moving a wire with current in a magnetic field, is equal to the product of the current and the increase of the magnetic flux due to the displacement of the wire.
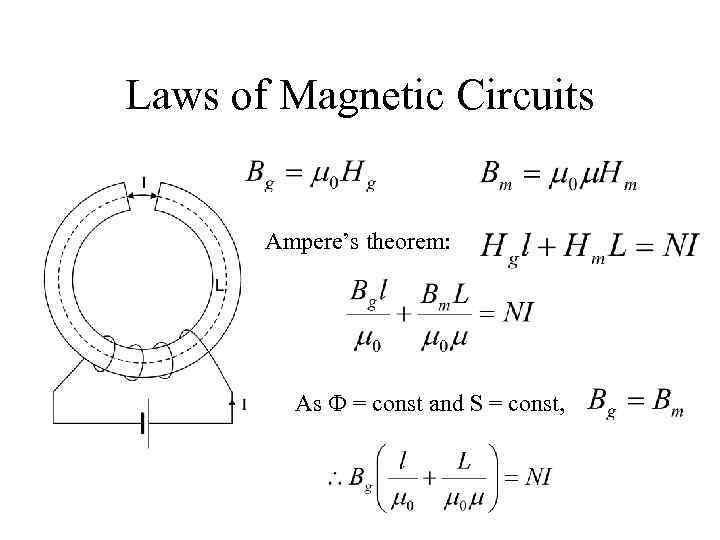Laws of Magnetic Circuits Ampere’s theorem: As Ф = const and S = const,
Laws of Magnetic Circuits (cont. ) NI is called usually the magnetomotive force, MMF. - is called the reluctance of the magnetic circuit.