L 29 E G Fields 1.pptx
- Количество слайдов: 27

Forces and Fields. By the end of the lecture… • Be able to quote Newton's Law of Universal Gravitation and Coulomb's Law • Know quantitative formulas which define the gravitational field strength, electric field strength. • Understand that field strength is a vector • Be familiar with the ideas of field lines, flux and flux density • Be able to perform a variety of calculations that demonstrate your understanding

Forces and Fields Gravitational Electric Strong nuclear (Weak nuclear) ^

Forces due to gravitation and charge Newton’s law of Gravitation Two particles m 1, m 2 distance r apart Coulomb’s law Two charges q 1, q 2 (in a vacuum) distance r apart

Force is along the line joining the masses or charges Each mass or charge experiences equal but opposite force (Newton’s 3 rd law) G is the Universal Gravitational constant G = 6. 67 x 10 -11 ε 0 is the permittivity of free space ε 0 = 8. 85 x 10 -12 Question: What are the units of G and ε 0 ?

Example 1: Suppose the electron and proton inside a hydrogen atom are point masses separated by 5. 29 x 10 -11 m. A) Find the Coulomb force FC and the gravitational force FG between them. B) What is the ratio of these forces? Data: electron charge = 1. 60 x 10 -19 C electron mass = 9. 11 x 10 -31 kg; proton mass = 1. 67 x 10 -27 kg

Example 2: A) For an electron orbiting the proton in the hydrogen atom, obtain an equation for the electron’s speed. B) Calculate the speed of the electron. C) Would we expect any relativistic effects at this speed?

Example 3: A satellite of mass ms is in a circular orbit of radius Rs around the Earth. If the Earth has mass M, show that the speed of the satellite is given by the expression:
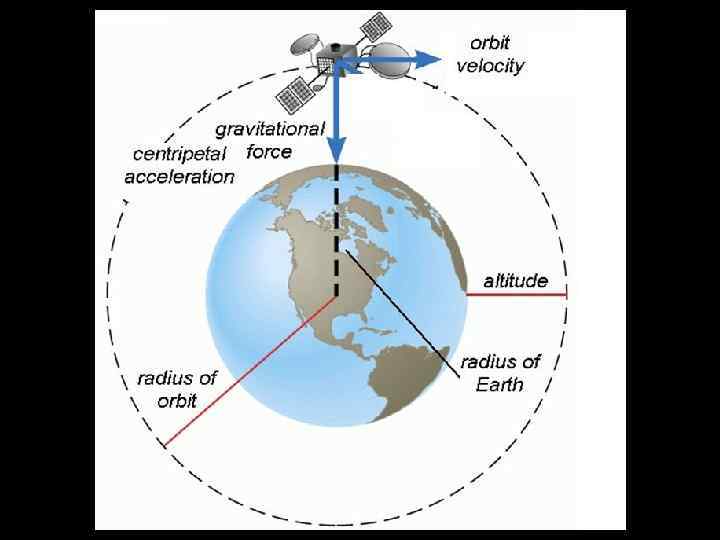

Fields – the concept A field means that we can assign a measurable physical property to every point in space (i. e. , 3 -D space). Question: Give examples of such measurable physical properties.

Temperature field

Pressure field

Magnetic field

Earth’s Magnetic Field

Electric Fields Consider we have 2 charges. Unlike the concept of direct interaction (Newton) we consider what happens in a two stage process: First, Q 1 changes the space around it; we say it creates a “field” around it (Faraday). Second, Q 2 interacts with the field of Q 1. Question: Is the force on Q 2 instantaneous?

How Do We Measure the Electric Field? We can detect the electric field by placing a small positive charge at any point in space, using:

Define “Electric Field” The E field is a vector whose magnitude is force per unit charge. The direction of the field is the direction of the force acting on a small positive “test” charge placed at that point.

Electric Field due to point charges For fields due to more than one charge, we use the principle of superposition. That is, at any given point in space, we add all E-fields as vectors.

Example 4: Two points charges, A of 2 n. C and B of -3 n. C are arranged as in the diagram. i) Find the magnitude and direction of the resultant electric field at P ii) If the charge at B is changed to + 3 n. C, at what distance from A on the line AB is the electric field strength zero?

Gravitational Field The force, FG, acting on a unit mass placed at each point in space. The gravitational field, g, due to a point mass

Uneven distribution of Earth’s gravitational field at surface.

Picturing E Field and G Fields • Electric Field lines or “lines of force”. • The tangent to a field line is the direction of the E field at that point. • The flux through an area is the total number of field lines that pass through the area. • The field lines are closer together where the field is greater, i. e. the flux density is greater. • Flux density is the number of lines of force per unit area where the area is perpendicular to the lines.

Field due to point charges − The flux density and therefore the E field obeys inverse square law. − Field lines start on positive charges and end on negative charges. − Field lines can never cross. pos neg


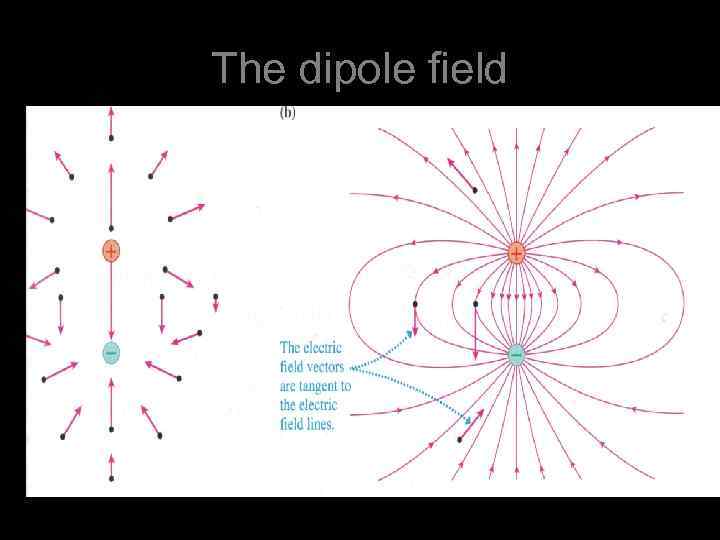
The dipole field

Example 5: Draw the field between two large parallel conducting plates (capacitor). - + + + http: //www. youtube. com/watch? v=DMz 3 Gte. Jf_4

Further Reading: Adams and Allday: 5. 1, 5. 2, 5. 7, 5. 9, 5. 14. Serway: 15. 1 -15. 5 • • • Be able to quote Newton's Law of Universal Gravitation and Coulomb's Law Know quantitative formulas which define the gravitational field strength, electric field strength, gravitational potential, electric potential. Understand that field strength is a vector Be familiar with the ideas of field lines, flux and flux density Know what an equipotential is Be able to perform a variety of calculations that demonstrate your understanding
L 29 E G Fields 1.pptx