dcc5a6823eb94398f362c0839cd04474.ppt
- Количество слайдов: 123

FOOD CHEMISTRYPractical-Demo BY DR BOOMINATHAN Ph. D. M. Sc. , (Med. Bio, JIPMER), M. Sc. , (FGS, Israel), Ph. D (NUS, SINGAPORE), PDF (USA) PONDICHERRY UNIVERSITY I lecture 6/7 August/2012 Source: Collected from different sources on the internet and presented by Dr L. Boominathan

PREPARING LABORATORY SOLUTIONS AND REAGENTS I THE BASICS

TOPICS • Where do solution recipes come from? • Concentration of solute: calculations • Preparing solutions – Making diluted solutions from concentrated ones – Buffers – Bringing solutions to proper p. H • Calculations for solutions with more than one solute, next lecture

WHERE DO SOLUTION "RECIPES" COME FROM? • Original Scientific Literature • Lab manuals (instructional) • Lab Manuals (professional) • Handbooks • Manufacturers and suppliers

INTERPRETING RECIPES DEFINITIONS: • SOLUTES -- substances that are dissolved • SOLVENTS -- substance in which solutes are dissolved (usually water) • AMOUNT -- how much

CONCENTRATION versus AMOUNT • CONCENTRATION -- amount / volume • Fraction where: – Numerator, the amount of solute – Denominator, usually volume of entire solution • solvent + solute(s)
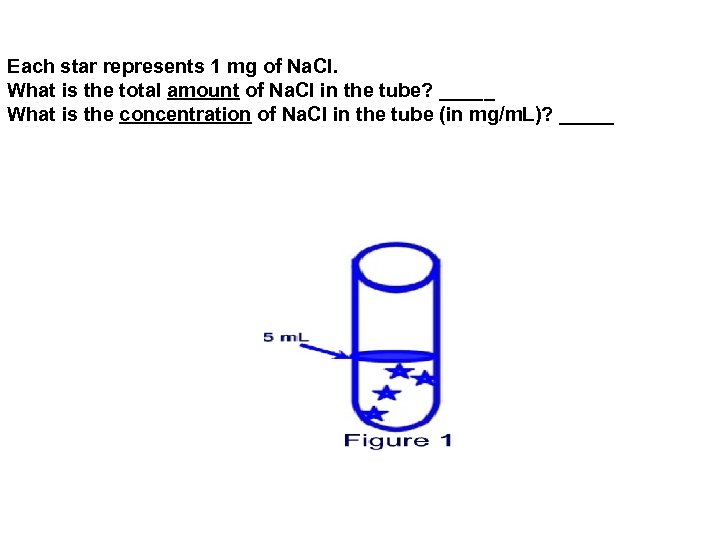
Each star represents 1 mg of Na. Cl. What is the total amount of Na. Cl in the tube? _____ What is the concentration of Na. Cl in the tube (in mg/m. L)? _____
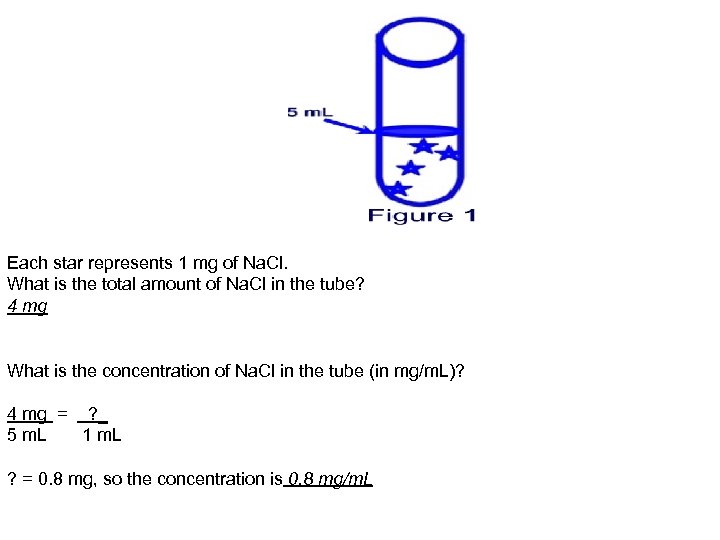
Each star represents 1 mg of Na. Cl. What is the total amount of Na. Cl in the tube? 4 mg What is the concentration of Na. Cl in the tube (in mg/m. L)? 4 mg = ? _ 5 m. L 1 m. L ? = 0. 8 mg, so the concentration is 0. 8 mg/m. L

WAYS TO EXPRESS CONCENTRATION OF SOLUTE • Source of confusion: more than one way to express concentration of solute in a solution

CONCENTRATION EXPRESSIONS 1. WEIGHT PER VOLUME 2. MOLARITY 3. PERCENTS a. Weight per Volume % (w/v %) b. Volume per Volume % (v/v %) c. Weight per Weight % (w/w %)

MORE CONCENTATION EXPRESSIONS 4. PARTS Amounts of solutes as "parts" a. Parts per Million (ppm) b. Parts per Billion (ppb) c. Might see ppt d. Percents are same category (pph %)

STILL MORE CONCENTRATION EXPRESSIONS TYPES NOT COMMON IN BIOLOGY MANUALS: 5. MOLALITY 6. NORMALITY • for Na. OH and HCl, molarity = normality, however, this is not always true for all solutes

WEIGHT / VOLUME • Means a fraction with: weight of solute in numerator total volume in denominator

EXAMPLE: • 2 mg/m. L proteinase K – 2 mg of proteinase K in each m. L of solution. • How much proteinase K is required to make 50 m. L of solution at a concentration of 2 mg/m. L?

PROPORTION PROBLEM 2 mg proteinase K 1 m. L solution = X 50 m. L solution X = 100 mg = amount proteinase K needed.

MOLARITY • Molarity is: number of moles of a solute that are dissolved per liter of total solution. • A 1 M solution contains 1 mole of solute per liter total volume.

MOLE • How much is a mole? From Basic Laboratory Methods for Biotechnology: Textbook and Laboratory Reference, Seidman and Moore, 2000

EXAMPLE: SULFURIC ACID For a particular compound, add the atomic weights of the atoms that compose the compound. H 2 SO 4: 2 hydrogen atoms 2 X 1. 00 g = 2. 00 g 1 sulfur atom 1 X 32. 06 g = 32. 06 g 4 oxygen atoms 4 X 16. 00 g = 64. 00 g 98. 06 g

EXAMPLE CONTINUED • A 1 M solution of sulfuric acid contains 98. 06 g of sulfuric acid in 1 liter of total solution. • "mole" is an expression of amount • "molarity" is an expression of concentration.

DEFINITIONS • "Millimolar", m. M, millimole/L. – A millimole is 1/1000 of a mole. • "Micromolar", µM, µmole/L. – A µmole is 1/1, 000 of a mole.

FORMULA HOW MUCH SOLUTE IS NEEDED FOR A SOLUTION OF A PARTICULAR MOLARITY AND VOLUME? (g solute ) X (mole) X (L) = g solute needed 1 mole L or FW X molarity x volume = g solute needed

EXAMPLE How much solute is required to make 300 m. L of 0. 8 M Ca. Cl 2?

ANSWER mole (111. 0 g) (0. 8 mole) (0. 3 L) = 26. 64 g L

From Basic Laboratory Methods for Biotechnology: Textbook and Laboratory Reference, Seidman and Moore, 2000

TO MAKE SOLUTION OF GIVEN MOLARITY AND VOLUME 1. Find the FW of the solute, usually from label. 2. Determine the molarity desired. 3. Determine the volume desired. 4. Determine how much solute is necessary by using the formula.

PROCEDURE CONT. 5. Weigh out the amount of solute. 6. Dissolve the solute in less than the desired final volume of solvent. 7. Place the solution in a volumetric flask or graduated cylinder. Add solvent until exactly the required volume is reached, Bring To Volume, BTV.

PERCENTS X % is a fraction numerator is X denominator is 100 Three variations on this theme.

WEIGHT/VOLUME TYPE I: Grams of solute 100 m. L total solution Most common in biology. %

EXAMPLE 20 g of Na. Cl in 100 m. L of total solution = 20% (w/v) solution.

EXAMPLE: BY PROPORTIONS How would you prepare 500 m. L of a 5 % (w/v) solution of Na. Cl?

ANSWER By definition: 5 % = 5 g 100 m. L 5 g = ? 100 m. L 500 m. L ? = 25 g = amount of solute BTV 500 m. L

BY EQUATION How would you prepare 500 m. L of a 5 % (w/v) solution of Na. Cl? 1. Total volume required is 500 m. L. 2. 5% = 0. 05 3. (0. 05) (500 m. L) = 25

% EXAMPLE CONTINUED 4. 25 is the amount of solute required in grams. 5. Weigh out 25 g of Na. Cl. Dissolve it in less than 500 m. L of water. 6. In a graduated cylinder or volumetric flask, bring the solution to 500 m. L.
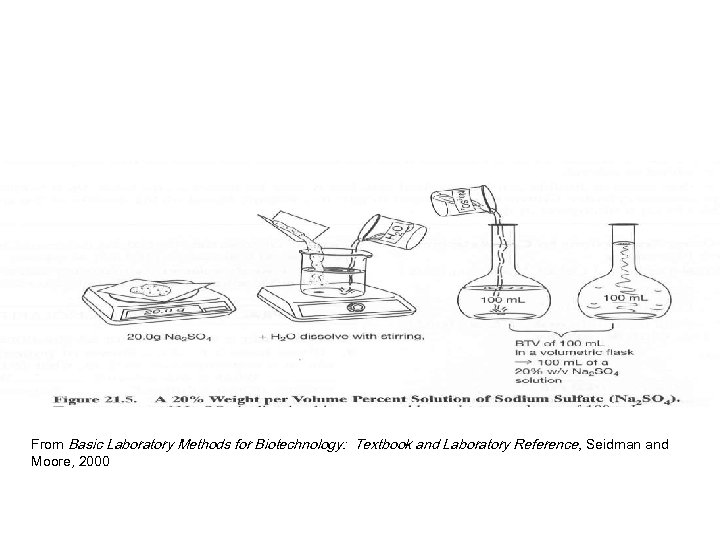
From Basic Laboratory Methods for Biotechnology: Textbook and Laboratory Reference, Seidman and Moore, 2000

TWO OTHER FORMS OF % v/v m. L solute 100 m. L solution w/w g solute 100 g solution

WEIGHT/WEIGHT • How would you make 500 g of a 5% solution of Na. Cl by weight (w/w)?

ANSWER 1. 2. Percent strength is 5% w/w, total weight desired is 500 g. 5% = 5 g/100 g 3. 5 g X 500 g = 25 g = Na. Cl needed 100 g 4. 500 g – 25 g = 475 g = amount of solvent needed 5. Dissolve 25 g of Na. Cl in 475 g of water.

PARTS Parts may have any units but must be the same for all components of the mixture.

EXAMPLE: A solution is 3: 2: 1 ethylene: chloroform: isoamyl alcohol Might combine: 3 liters ethylene 2 liters chloroform 1 liter isoamyl alcohol

PPM AND PPB • ppm: The number of parts of solute per 1 million parts of total solution. • ppb: The number of parts of solute per billion parts of solution.

PPM EXAMPLE: 5 ppm chlorine = 5 g of chlorine in 1 million g of solution, or 5 mg chlorine in 1 million mg of solution, or 5 pounds of chlorine in 1 million pounds of solution

CONVERSIONS To convert ppm or ppb to simple weight per volume expressions: 5 ppm chlorine = 5 g chlorine = 106 g water 5 g chlorine 106 m. L water = 5 mg/1 L water = 5 X 10 -6 g chlorine/ 1 m. L water = 5 micrograms/m. L

PPM TO MICROGRAMS/m. L For any solute: 1 ppm in water = 1 microgram m. L
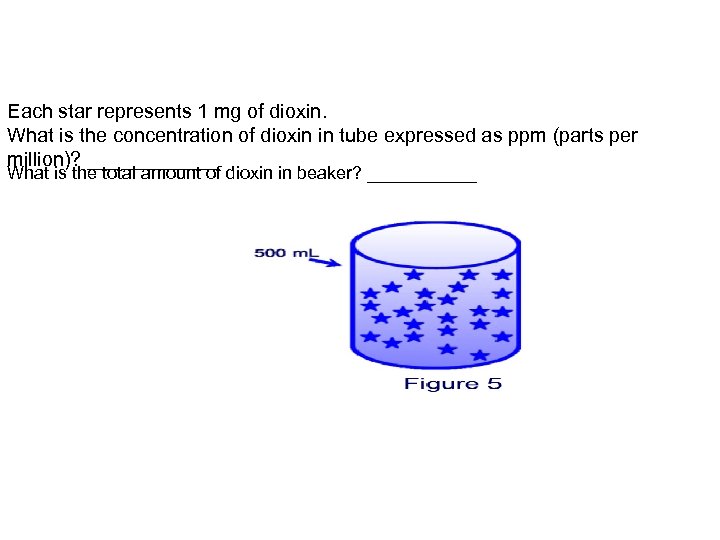
Each star represents 1 mg of dioxin. What is the concentration of dioxin in tube expressed as ppm (parts per million)? ______ What is the total amount of dioxin in beaker? ______
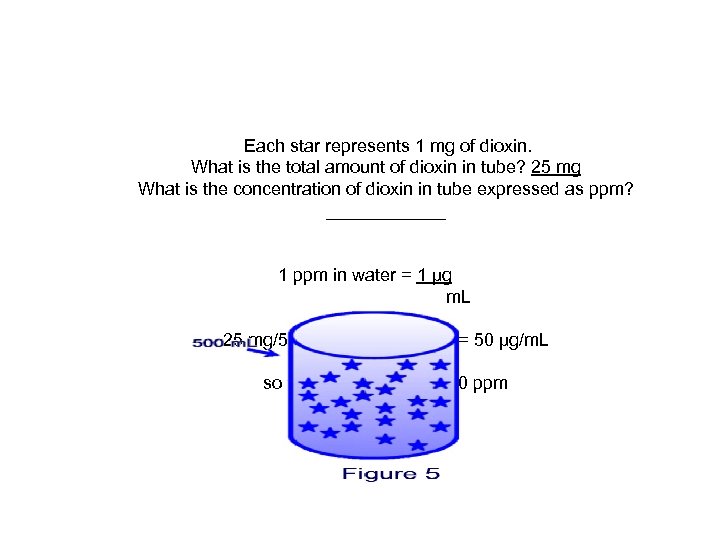
Each star represents 1 mg of dioxin. What is the total amount of dioxin in tube? 25 mg What is the concentration of dioxin in tube expressed as ppm? ______ 1 ppm in water = 1 μg m. L 25 mg/500 m. L = 0. 05 mg/m. L = 50 μg/m. L so the concentration is 50 ppm


PREPARATION OF SOLUTIONS • Preparing Dilute Solutions from Concentrated Ones (C 1 V 1=C 2 V 2) • Biological Buffers • Preparing Solutions with More Than One Solute • Assuring the Quality of a Solution

PREPARING DILUTE SOLUTIONS FROM CONCENTRATED ONES • Concentrated solution = stock solution • Use this equation to decide how much stock solution you will need: C 1 V 1=C 2 V 2 C 1 = concentration of stock solution C 2 = concentration you want your dilute solution to be V 1 = how much stock solution you will need V 2 = how much of the dilute solution you want to make

EXAMPLE • How would you prepare 1000 m. L of a 1 M solution of Tris buffer from a 3 M stock of Tris buffer? – The concentrated solution is 3 M, and is C 1. – The volume of stock needed is unknown, ? , and is V 1. – The final concentration required is 1 M, and is C 2. – The final volume required is 1000 m. L and is V 2.

SUBSTITUTING INTO THE EQUATION: C 1 V 1 = C 2 V 2 3 M (? ) 1 M (1000 m. L) ? = 333. 33 m. L So, take 333. 33 m. L of the concentrated stock solution and BTV 1 L.

“X” SOLUTIONS • The concentration of a stock solution is sometimes written with an “X”. • The “X” is how many more times the stock is than normal. • You generally want to dilute such a stock to 1 X, unless told otherwise.

EXAMPLE • A can of frozen orange juice is labeled 4 X. How would you dilute it to make 1 L of drinkable juice? • Using the C 1 V 1=C 2 V 2 equation: C 1 V 1 = C 2 V 2 4 X (? ) = 1 X (1 L) ? = 0. 25 L Use 0. 25 L of orange juice, BTV 1 L.

BIOLOGICAL BUFFERS • Laboratory buffers solutions to help maintain a biological system at proper p. H • p. Ka of a buffer the p. H at which the buffer experiences little change in p. H with addition of acids or bases = the p. H at which the buffer is most useful

TEMPERATURE • Some buffers change p. H as their temperature and/or concentration changes • Tris buffer, widely used in molecular biology, is very sensitive to temperature

DILUTION • Some buffers are sensitive to dilution • Phosphate buffer is sensitive to dilution

ADJUSTING THE p. H of a BUFFER • This is done to set the buffer to a p. H value which is. . . – somewhat close to its p. Ka – useful for the biological system the buffer is to be used with • Often adjust p. H using Na. OH or HCl – Not method used for phosphate buffer (see textbook)

BRINGING A SOLUTION TO THE PROPER p. H • Adjust the p. H when the solution is at the temperature at which you plan to use it. • Mix the solute(s) with most, but not all, the solvent. Do not bring the solution to volume. • Stir solution.

• Check the p. H. • Add a small amount of acid or base. – The recipe may specify which to use. – If not, HCl and Na. OH are commonly used. • Stir again and then check the p. H.


• Repeat until the p. H is correct, but don’t overshoot. • Bring the solution to volume and recheck the p. H.

ASSURING THE QUALITY OF A SOLUTION • Documentation, labeling, recording what was done • Traceability • SOPs • Maintenance and calibration of instruments • Stability and expiration date recorded • Proper storage

Solution Chemistry It’s all about the concentration

Common units of concentration % by mass – g solute /100 g solution % by volume – m. L solute/100 m. L solution % by mass-volume – g solute/100 m. L solution Molarity – moles solute/L solution Molality – moles solute/kg solvent Normality – equivalent moles of solute/L solution ppt – grams solute/thousand grams solution ppm –g solute/million g solution ppb – g solute/billion g solution lb solute/million gallons solution

Some conversion problems: Convert 136 μg Na. Cl/m. L pond water to lb Na. Cl/million gallons pond water.

Some conversion problems: 136 μg Na. Cl …. ? lb Na. Cl m. L pond water million gallons pond water What do we need to know?

Some conversion problems: 136 μg Na. Cl …. ? lb Na. Cl m. L pond water million gallons pond water What do we need to know? • • How many μg in a lb? How many m. L in a million gallons?

Some conversion problems: 136 μg Na. Cl …. ? lb Na. Cl ml pond water million gallons pond water 453. 6 g = 1 pound 1 μg = 10 -6 g 1 m. L = 10 -3 L 1. 057 L = 1 quart 4 quarts = 1 gallon

Some conversion problems: 136 μg Na. Cl * 10 -6 g * 1 lb = 2. 998 x 10 -7 lb m. L pond water 1 μg 453. 6 g m. L pond water 2. 998 x 10 -7 lb * 1 m. L * 1. 057 L = 3. 17 x 10 -4 lb m. L pond water 10 -3 L 1 qt qt 3. 17 x 10 -4 lb * 4 qt * 106 gal = 1. 26 x 103 lb qt 1 gal million gal

Some conversion problems: Convert 36% by mass of HCl to Molarity. How do we start?

Some conversion problems: Convert 36% by mass of HCl to Molarity. How do we start? Units!

Some conversion problems: Convert 36% by mass of HCl solution to Molarity. 36 g HCl ……. . 100 g solution Moles HCl 1 L solution What do we need to know?

Some conversion problems: Convert 36% by mass of HCl solution to Molarity. 36 g HCl ……. . 100 g solution Moles HCl 1 L solution What do we need to know? • Molar mass of HCl • Density of HCl solution

Some conversion problems: Convert 36% by mass of HCl solution to Molarity. 36 g HCl ……. . 100 g solution Moles HCl 1 L solution What do we need to know? • Molar mass of HCl (36. 46 g/mol – from Periodic table) • Density of HCl solution (from where? ? ? )

Density – your critical judgment For a solution, sometimes you know the density, sometimes you don’t. There are tables, but they are not all inclusive. You might, for example, find in a table that: Density (30% HCl) = 1. 12 g/m. L Density (40% HCl) = 1. 23 g/m. L Density (36% HCl) = ? ? ?

Interpolate or Assume Density (30% HCl) = 1. 12 g/m. L Density (40% HCl) = 1. 23 g/m. L Density (36% HCl) = ? ? ? You could assume that 36% is closest to 40% and use 1. 23 g/m. L. This is legitimate, although not 100% accurate. Results may vary, depending on how good the assumption is.

Interpolate or Assume Density (30% HCl) = 1. 12 g/m. L Density (40% HCl) = 1. 23 g/m. L Density (36% HCl) = ? ? ? You could assume that density changes linearly with concentration (it doesn’t, but it is pseudo-linear for small changes). In that case, you would “linearly interpolate” the density. 1. 23 g/m. L – 1. 12 g/m. L = 0. 011 g 40% HCl-30%HCl % m. L% 1. 12 g/m. L + 0. 011 g/m. L% * 6% = 1. 186 g/m. L = 1. 19 g/m. L This is legitimate, although still not 100% accurate, but probably better than the previous assumption.

If I don’t have Density tables… For dilute solutions, you can get pretty close by assuming the density of the solution is the same as the density of pure water. For concentrated solutions (like 36%), this is probably not a good assumption, but it is better than nothing!

Solving the problem (finally) Convert 36% by mass of HCl solution to Molarity. 36 g HCl ……. . 100 g solution Moles HCl 1 L solution What do we need to know? • Molar mass of HCl (36. 46 g/mol – from Periodic table) • Density of HCl solution (1. 19 g/m. L – by assuming linear change)

Solving the problem (finally) 36 g HCl * 1 mol * 1. 19 g * 1000 m. L 100 g sol 36. 46 g 1 m. L 1 L solution = 11. 7 mol HCl L solution = 11. 7 M HCl (if you don’t specify solvent, usually assumed to be water)

Common units of concentration % by mass – g solute /100 g solution % by volume – m. L solute/100 m. L solution % by mass-volume – g solute/100 m. L solution Molarity – moles solute/L solution Molality – moles solute/kg solvent Normality – equivalent moles of solute/L solution ppt – grams solute/thousand grams solution ppm –g solute/million g solution ppb – g solute/billion g solution lb solute/million gallons solution

All are important, but… Moles! Molarity – moles solute/L solution (most common) Molality – moles solute/kg solvent (not very common) Normality – equivalent moles of solute/L solution (specialized usage) What’s “equivalent moles”?

Normality vs. Molarity = moles solute/L solution - generic, just the moles folks Normality = equivalent moles of solute/L solution - specific, it takes into account the actual chemistry of the solute.

Acids What’s an acid?

Acids What’s an acid? Within the Bronsted-Lowry theory of acids/bases, an acid is a proton (H+) donor and a base is a proton acceptor. Can you think of examples of acids or bases?

Some acids and bases Na. OH – base Mg(OH)2 – base HCl – acid (hydrochloric acid) HF – acid (hydrofluoric acid) H 2 SO 4 – acid (sulfuric acid)

Acid – what’s it good for? ? ?

Acid – what’s it good for? Protons If we define an acid as a proton donor, the proton is what makes it what it is.

Consider two solutions: 1 M HCl 1 M H 2 SO 4 How are they the same? How are they different?

Consider two solutions: 1 M HCl 1 M H 2 SO 4 1 molecules/L

Consider two solutions: 1 M HCl 1 M H 2 SO 4 1 molecules/L H+ Cl- in solution 1 molecules/L H+ and SO 42 - in solution HCl(aq) → H+(aq) + Cl-(aq) H 2 SO 4 (aq) HCl(aq) + H 2 O(l) H 2 SO 4 (aq) + → H 3 O+(aq) + Cl-(aq) → 2 H+ (aq) + SO 42 -(aq) 2 H 2 O(l)→ 2 H 3 O+ (aq) + SO 42 -(aq)

Consider two solutions: 1 M HCl 1 M H 2 SO 4 1 molecules/L H+ Cl- in solution 1 molecules/L H+ and SO 42 - in solution HCl(aq) → H+(aq) + Cl-(aq) H 2 SO 4 (aq) HCl(aq) + H 2 O(l) H 2 SO 4 (aq) + → H 3 O+(aq) + Cl-(aq) 1 mol H+/L solution → 2 H+ (aq) + SO 42 -(aq) 2 H 2 O(l)→ 2 H 3 O+ (aq) + SO 42 -(aq) 2 mol H+/L solution

Consider two solutions: 1 M HCl 1 M H 2 SO 4 1 molecules/L 1 mole H+/L solution 1 molecules/L 2 mol H+/ L solution They are both acids, they are defined by their ability to donate protons. The protons are the “equivalents” for an acid. 1 N HCl 2 N H 2 SO 4

Lab Exercise 0 ne Carbohydrate Analysis: Estimation of Sugars Lab

Biochemical Assay • Biochemistry deals with the identification and quantification of bio-molecules from a variety of living systems • Rely on the chemical reactivity and physical properties of bio-molecules to make identification and quantification. • Primary tool is the spectrophotometer – Uses absorption of mono chromatic light
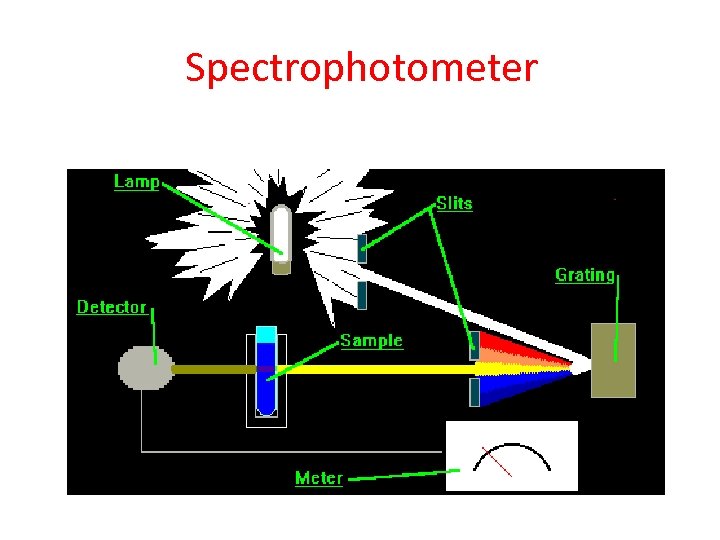
Spectrophotometer

Measure quantity • Some bio-molecules have properties which allow direct measurement. – proteins have aromatic amino acids (280 nm) – Nucleic acids have unsaturated ring structures (260 nm) • Other molecules have chemical properties which can be used in indirect measurement.

Introducing concept of standard curve • Uses dilutions of a solution of known concentration to determine concentration of unknown

Standard Curve • Assumes that unknown will respond in assay the same as the known – Valid in todays assay as they (the reactive groups. glucose) are the same – Problem in other assay as they may not contain same amount of reactive groups • Protein assays (have to choose) • But usually close

Our model carbohydrate is the sugar glucose We will exploit its ability to reduce other compounds to produce a product which can be measured optically
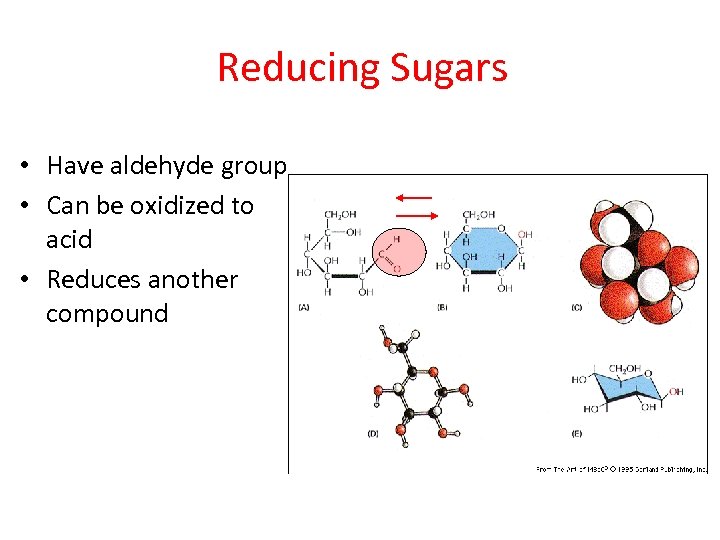
Reducing Sugars • Have aldehyde group • Can be oxidized to acid • Reduces another compound

Requirement placed on sugar • Must be an aldehyde – Ketones and hemiacetal configurations are not reducing • Conditions of reactions favor conversion to aldehyde by lowering aldehyde concentration
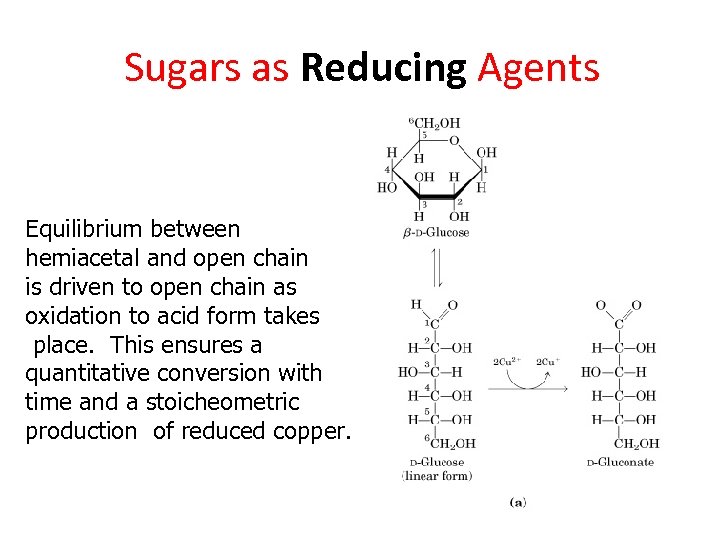
Sugars as Reducing Agents Equilibrium between hemiacetal and open chain is driven to open chain as oxidation to acid form takes place. This ensures a quantitative conversion with time and a stoicheometric production of reduced copper.

Nelson Assay (a two step Rx) • In the Nelson assay Cu+2 is reduced to Cu+1 by the reducing activity of the sugar (step 1) • Cu+1 is oxidized to Cu+2 by addition of arsenomolybdic acid (colorless) (step 2) • Results in blue (reduced) arsenomolybdous acid • Amount is directly related to [CU+1] • Will detect any reducing sugar (concentration of sugar must be limiting factor)

We will do the DNS assay • Is a direct assay • Measures the reducing capability of glucose • Uses a color conversion reaction from yellow to red brown @ A 540 • Conversion of moles of DNS equals moles of glucose.

3, 5 -dinitrosalicylic acid (DNS) • Sugar reduces the organic DNS which absorbs maximally at yellow wave length • Results in change (shift) in absorption spectrum from red/orange to red/brown at 540 nm – Different from Nelson reaction • Measured at 540 nm – Unreacted DNS not seen at this wavelength – Amount of absorbance directly related to amount of reducing sugar
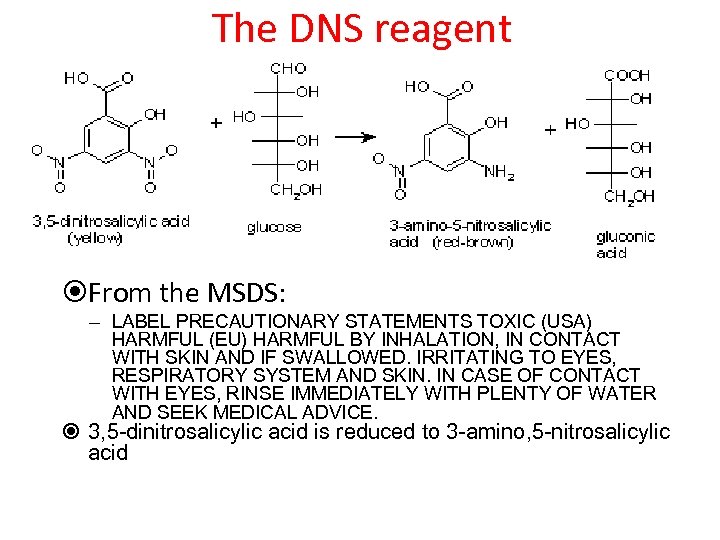
The DNS reagent From the MSDS: – LABEL PRECAUTIONARY STATEMENTS TOXIC (USA) HARMFUL (EU) HARMFUL BY INHALATION, IN CONTACT WITH SKIN AND IF SWALLOWED. IRRITATING TO EYES, RESPIRATORY SYSTEM AND SKIN. IN CASE OF CONTACT WITH EYES, RINSE IMMEDIATELY WITH PLENTY OF WATER AND SEEK MEDICAL ADVICE. 3, 5 -dinitrosalicylic acid is reduced to 3 -amino, 5 -nitrosalicylic acid

The DNS assay • Experimental design and flow charts • Be sure to read “Hazards” • Data analysis

Today's Experiment • Measure the concentration of glucose by detecting the reducing end of the monosaccharide. • This group converts the oxidized form of 3, 5 dinitrosalicylic acid, DNS, to reduced form which absorbs at 540 nm. • Amount of reduced DNS proportional to amount of glucose.
What are we doing today?

Important • Pipetting technique is critical to accuracy and to preventing cross contamination of samples – Pipetters have two stops • First to take up selected volumes • Second to deliver • Choose pipetter “in the range” that you need.

You will create a standard curve • You are provided a stock solution which contains 1. 2 mg/ml • You will dilute this stock solution in a specified manner always producing a 4 ml solution • You will read the absorbance of each solution at 540 and plot vs concentration • You will compare the A 540 of unknown to standard curve
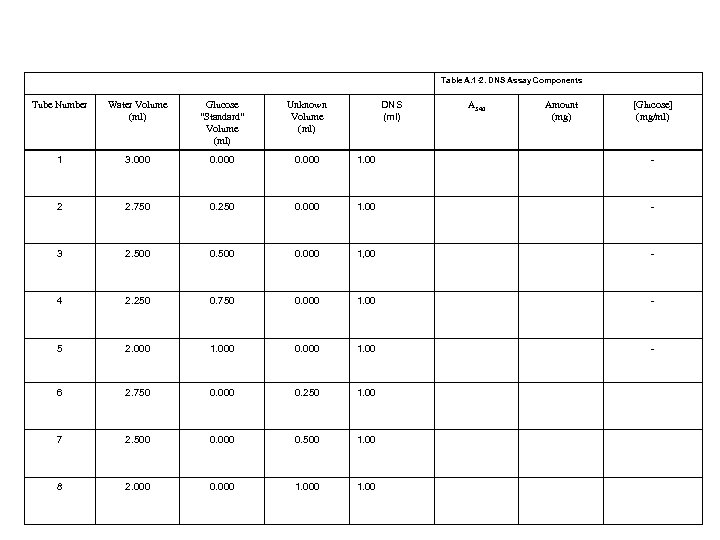
Table A. 1 -2. DNS Assay Components DNS (ml) Tube Number Water Volume (ml) Glucose “Standard” Volume (ml) Unknown Volume (ml) A 540 Amount (mg) [Glucose] (mg/ml) 1 3. 000 0. 000 1. 00 - 2 2. 750 0. 250 0. 000 1. 00 - 3 2. 500 0. 000 1, 00 - 4 2. 250 0. 750 0. 000 1. 00 - 5 2. 000 1. 000 0. 000 1. 00 - 6 2. 750 0. 000 0. 250 1. 00 7 2. 500 0. 000 0. 500 1. 00 8 2. 000 0. 000 1. 00

Standard curve • Uses dilutions of a solution of known concentration to determine concentration of unknown

Important • Careful handling of Cuvettes is essential for accuracy and prevent contamination – Handle only with gloves – Touch only the areas not in the light path – Rinse carefully with DH 2 O after each use – Always go from lowest concentration to highest concentration. – Wipe clear surface if necessary with “Kimwipe”

Extremely Important • • Put cuvette into Spec slot that is in the beam path Be certain that clean panes face the beam path Measure only with the lid closed Always set the spec with a blank (line 1 table A. 1 -2, page 38) – Contains all components of reaction except that which is to be measured – Always use same cuvette

PLEASE DO NOT SLAM THE SPEC LIDS

Important • • • 1. Wear Gloves and Safety Glasses 2. Record the code number of your unknown 3. Be certain that test tubes are clean 4. Water/H 2 O always means distilled water 5. Have TA initial your data before you leave. See lab exit requirements page

Lab reports for this class • Abstract. Statements regarding: – – WHAT you are doing (-> procedure) WHY you are doing it (-> your hypothesis) WHAT you hope to accomplish (-> also hypothesis) Cf. ‘purpose/goal’ in a good lab notebook! Might think of it as a very short introduction • Background information and theory • Results/Data Analysis • Discussion MUST relate data analysis to hypothesis!

Application quiz Address in your report • What does the portable glucometers used by diabetics measure? • How do they measure it?

Reminder • Lab Reports are PERSONAL

Grading for This Experiment • • Number of lab periods = 1 Lab Report = points Pre lab= points Total = points

Clean up (Please) before you go • See page 44. Waste Disposal & Clean up • Return pipetts to rack
dcc5a6823eb94398f362c0839cd04474.ppt