• ФОНАРЬ
• СОВЕСТЬ
НАУКА
• Составьте и запишите истинные сложные высказывания из простых с использованием логических операций. • 1. Неверно, что 10>Y>5 и Z<0 • Y < 10) & (Y > 5) & (Z< 0). • 2. Z является min(Z, Y) • : Z
• 4. Любое из чисел X, Y, Z положительно • (X>0)v(Y>0)v(Z>0). • 5. Любое из чисел X, Y, Z отрицательно • (X<0)v(Y<0)v(Z<0). • 6. Хотя бы одно из чисел K, L, M не отрицательно • (К > 0) v (I > 0) v(M > О) • 7. Хотя бы одно из чисел X, Y, Z не меньше 12 • (X > 12) v(Y > 12) v (Z > 12)
• 8. Все числа X, Y, Z равны 12 • (X=12)&(Y=12)&(Z=12) • 9. Если X делится на 9, то X делиться и на 3 (X делится на 9)→(X делится на 3) • 10. Если X делится на 2, то оно четное • ((X делится на 2)→(X - четное)).
1. 2. 3. 4. 5. СОДЕРЖАНИЕ ОПРЕДЕЛЕНИЕ СОСТАВ ВИДЫ ПРИМЕРЫ РЕШЕНИЕ ЗАДАЧ
• Все знания о мире делятся на непосредственные (эмпирические) и опосредованные (выводные). • В первом случае это результат непосредственного изучения окружающего мира. • Но большая часть знаний получается опосредованно, выводным путем, путем логической обработки опытного материала
• Например: зная, что все продукты, изготовленные для продажи – товар, а машина – тоже продукт, делаем вывод о ее товарном характере. Вывод об этом свойстве получается путем умозаключения, с помощью которого из содержания исходных суждений извлекается новое знание
это форма мышления, позволяющая из одного или нескольких суждений, называемых посылками, извлекать с помощью правил логики новое суждение заключение
ТЕХНОЛОГИЯ УМОЗАКЛЮЧЕНИЯ • Путь вывода умозаключений лежит через … • Рассуждение – это цепочка взаимосвязанных суждений, фактов и общих положений по определенным правилам вывода.
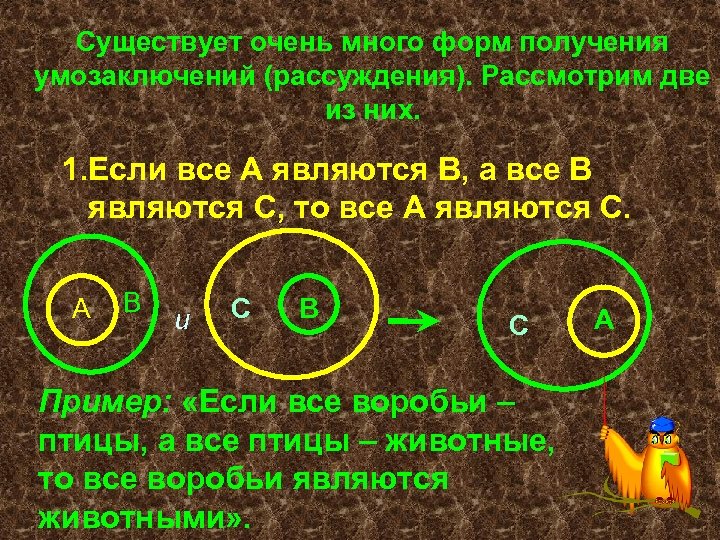Существует очень много форм получения умозаключений (рассуждения). Рассмотрим две из них. 1. Если все А являются В, а все В являются С, то все А являются С. А В и С В С Пример: «Если все воробьи – птицы, а все птицы – животные, то все воробьи являются животными» . А
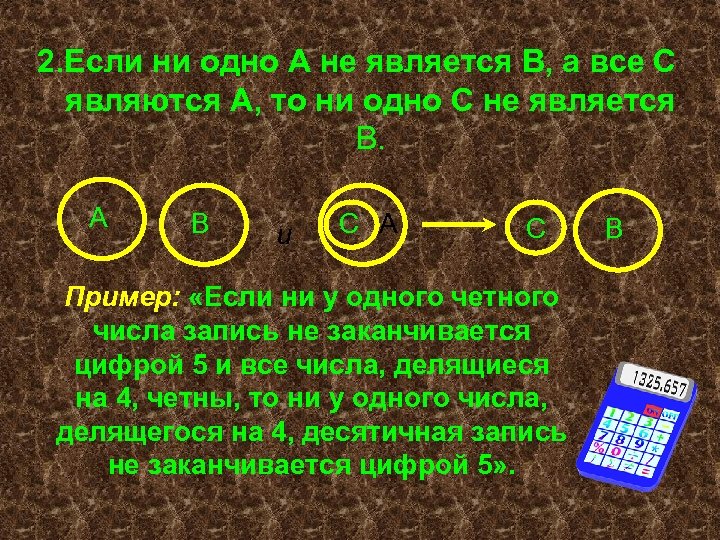2. Если ни одно А не является В, а все С являются А, то ни одно С не является В. А В и С А С Пример: «Если ни у одного четного числа запись не заканчивается цифрой 5 и все числа, делящиеся на 4, четны, то ни у одного числа, делящегося на 4, десятичная запись не заканчивается цифрой 5» . В
• На стадии умозаключения о вещах можно рассуждать, не обращаясь к ним самим. Достаточно иметь о них несколько верных высказываний. По этой причине, опираясь на правила умозаключения, наука получает возможность рассуждать о природных явлениях теоретически, постигать те их стороны, которые скрыты за внешней, доступной наблюдению поверхностью, проникать в недоступные природные глубины, обращаться мыслью в такие запредельные дали, которые можно изучать лишь умозрительно. Палеонтологам иной раз хватает одной кости для воссоздания всего облика давно вымерших животных. Например, Демокрит догадался о существовании атомов, наблюдая, как истираются со временем каменные ступени храма. Много великих и малых тайн природы разгадано благодаря тонким и сложным рассуждениям. обширные теории.
ПРИМЕР • Возьмем для наглядности такое рассуждение: • Если число 64 делится на 3 и на 4, то оно делится на 12. • Число 64 не делится на 12. • Следовательно, число 64 не делится на 3 или на 4. • При такой схеме рассуждения из высказываний, составляющих первые две строчки, с необходимостью вытекает третья строчка. Или например: если дует сильный ветер и падает снег, то значит на улице пурга; но пурги нет; следовательно, на улице не падает снег или нет ветра
Структура умозаключения • Любое умозаключение состоит из: • Посылок – исходных суждений, из которых выводится новое суждение. • Заключения – нового суждения, полученного логическим путём из посылок. • Вывода – логического перехода от посылок к заключению
• Посылки - это исходное и притом уже известное, знание, служащее основанием умозаключения.
• Заключение - производное, притом новое, полученное из посылок и выступающее их следствием. • Заключение будет истинным при наличии двух необходимых условий: во-первых, должны быть истинными исходные суждения - посылки умозаключения; во-вторых, в процессе рассуждения следует соблюдать правила вывода, которые обуславливают логическую правильность умозаключения •
• Вывод (лат. CONCLUSIO) — процесс РАССУЖДЕНИЯ, в ходе которого осуществляется переход от некоторых исходных СУЖДЕНИЙ (предпосылок) к новым суждениям — ЗАКЛЮЧЕНИЯМ. • Правила преобразования исходной системы предпосылок в систему заключений называются правилами вывода или правилами проведения умозаключений. Если вид посылок и заключений указан явно, то вывод называется прямым. Если в посылках и заключении указаны лишь виды выводов, от одного из которых разрешается переходить к другому, то вывод называют косвенным.
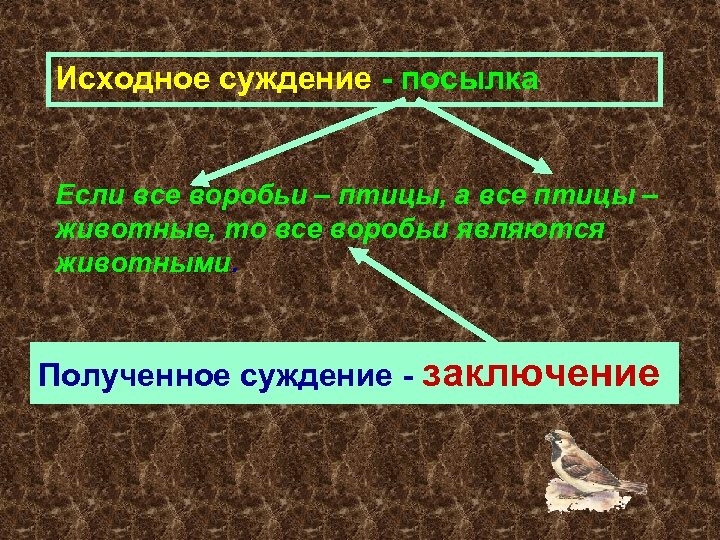Исходное суждение - посылка Если все воробьи – птицы, а все птицы – животные, то все воробьи являются животными. Полученное суждение - заключение
пример: • «Судья не может участвовать в рассмотрении дела, если он является потерпевшим (1). Судья Н. — потерпевший (2). Значит, судья Н. не может участвовать в рассмотрении дела (3)» . • В этом умозаключении 1 -е и 2 -е суждения являются посылками, 3 -е суждение — заключением
• Умозаключения разделяют по признакам • По направлению логического следования • По достоверности вывода • По числу посылок.
По направлению логического следования – ДЕДУКТИВНЫЕ (от общего к частному). – ИНДУКТИВНЫЕ (от частного к общему). – ТРАНСДУКТИВНЫЕ (от одной степени общности к такой же степени общности).
• Дедукция (от латинского deductio - "выведение") - это умозаключение, в котором переход от общего знания к частному является логически необходимым. • Правила дедуктивного вывода определяются характером посылок, которые могут быть простыми или сложными суждениями. • В зависимости от количества посылок дедуктивные выводы делятся на непосредственные, в которых заключение выводится из одной посылки, и опосредственные, в которых заключение выводится из нескольких (двух и более) посылок. • Пример: • Все металлы проводят электричество. • Медь - металл. • Медь проводит электричество. •
это умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности к классу в целом. • ИНДУКЦИЯ (от латинского inductio - "наведение") - • Основная функция индуктивных выводов в процессе познания генерализация, т. е. получение общих суждений. По своему содержанию и познавательному значению эти обобщения могут носить различный характер - от простейших обобщений повседневной практики до эмпирических обобщений в науке или универсальных суждений, выражающих всеобщие законы. В зависимости от полноты и закономерности эмпирического исследования различают два вида индуктивных умозаключений: полную индукцию и неполную индукцию. • Пример: определив, что каждый металл проводит электричество, можно сделать вывод: "Все металлы проводят электричество".
• ТРАНСДУКЦИЯ (от латинского traductio "перевод", "перемещение", "перенос") - это умозаключение по аналогии, то есть вывод о принадлежности определенного признака исследуемому единичному объекту (предмету, событию, отношению или классу) на основе его сходства в существенных чертах с другим уже известным единичным объектом. • • Умозаключению по аналогии всегда предшествует операция сравнения двух объектов, которая позволяет установить сходства и различия между ними. При это для аналогии требуются не любые совпадения, а сходства в существенных признаках при не существенности различий. Именно такие сходства служат для уподобления двух материальных или идеальных объектов. В качестве примера можно привести в истории физики о механизмах распространении звука и света, когда их уподобили движению жидкости. На основе этого возникли волновые теории звука и света. Объектами уподобления в этом случае были жидкость, звук и свет, а переносимым признаком волновой способ их распространения.
По достоверности вывода. – Достоверные. – Правдоподобные
• . Непосредственные. – Опосредственные
• Непосредственные умозаключения - это такие умозаключения, которые делаются из одной посылки, полученное посредством • • преобразования некоторого суждения. К ним относятся: 1) превращение, 2) обращение, 3)противопоставление предикату, 4)умозаключение по логическому квадрату. Выводы в каждом из этих умозаключений получаются в соответствии с логическими правилами, которые обусловлены видом суждения - его количественными и качественными характеристиками. Например, из суждения «Все адвокаты - юристы» можно получить новое суждение «Некоторые юристы - адвокаты» . Непосредственные умозаключения дают нам возможность выявить знание о таких сторонах предметов, которое уже содержалось в исходном суждении, но не было явно выражено и явно осознано. В этих условиях мы делаем неявное - явным, неосознанное - осознанным
Обратите внимание ПАРАЛОГИЗМ СОФИЗМ ПАРАДОКС
Паралогизм - умозаключение, содержащее непреднамеренную ошибку. Паралогизмы допускают многие люди. Часто паралогизмы встречаются в контрольных работах учащихся.
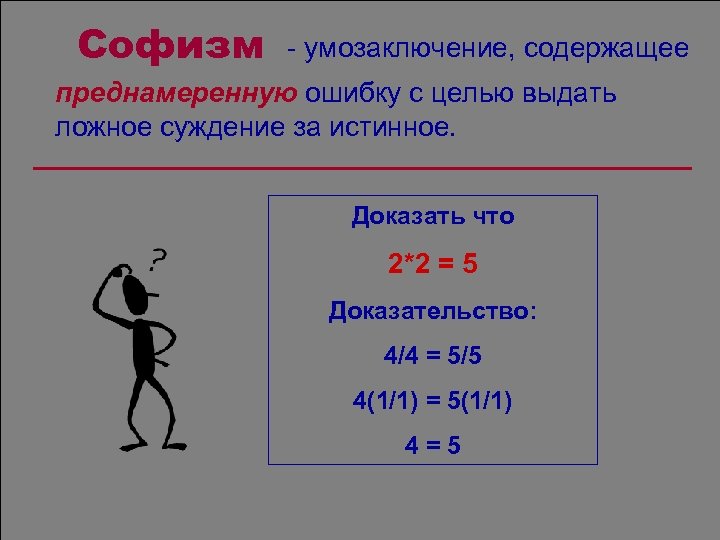Софизм - умозаключение, содержащее преднамеренную ошибку с целью выдать ложное суждение за истинное. Доказать что 2*2 = 5 Доказательство: 4/4 = 5/5 4(1/1) = 5(1/1) 4=5
Парадокс - умозаключение, доказывающее как истинность, так и ложность некоторого суждения. Парадокс «Генерал и брадобрей» Каждый солдат может сам себя брить или бриться у другого солдата. Генерал приказал выделить одного специального солдата-брадобрея, у которого брились бы только те солдаты, которые себя не бреют. Кто должен брить солдатабрадобрея? Себя он брить не может, так как бреет только тех солдат, которые себя не бреют. Если он не будет себя брить, то по приказу должен бриться у назначенного солдата-брадобрея, т. е. у себя.
• Задача 1 Шла с рынка бабушка, в руках у нее была корзинка с яйцами. • Проходящий мимо барин, толкнул ее, корзинка упала и яйца разбились. • Барину стало неудобно и он предложил возьместить убыток, спросил, сколько было яиц, чтобы заплатить ей. Бабушка была склерозница, поэтому точно не помнила сколько же их было, но в молодости она была математиком. . . • Поэтому бабушка сказала честно, что не знает, но она пыталась разделить их на 2, 3, 4, 5, 6, 7 и 8 кучек, но всегда оставалось одно яйцо! • Вопрос: Сколько яиц у нее было?