2e36e53d13af9908a580f078348a5ac2.ppt
- Количество слайдов: 47
 FNCE 4070 Financial Markets and Institutions Lecture 5: Part 1 Term Structure of Interest Rates (Yield Curves) Constructing and Explaining Yield Curves (Theories of the Yield Curve)
FNCE 4070 Financial Markets and Institutions Lecture 5: Part 1 Term Structure of Interest Rates (Yield Curves) Constructing and Explaining Yield Curves (Theories of the Yield Curve)
 Relationship of Yields to Maturity n n In lecture 4 we discussed factors, such as inflationary expectations, risk of default, business cycles, flight to safety, and term to maturity, which can affect market interest rates. In this lecture we will expand on term to maturity as a factor and specifically how we can use yield curves. q Recall that term to maturity refers to the time when a financial asset matures (i. e. , when the issuer will retire the asset). n Thus, term to maturity and yield curves are relevant to fixed income securities, such as bonds, where there is a stated maturity date.
Relationship of Yields to Maturity n n In lecture 4 we discussed factors, such as inflationary expectations, risk of default, business cycles, flight to safety, and term to maturity, which can affect market interest rates. In this lecture we will expand on term to maturity as a factor and specifically how we can use yield curves. q Recall that term to maturity refers to the time when a financial asset matures (i. e. , when the issuer will retire the asset). n Thus, term to maturity and yield curves are relevant to fixed income securities, such as bonds, where there is a stated maturity date.
 Initial Observations: Does Maturity Matter n Yes, generally long term interest rates are above short term interest rates
Initial Observations: Does Maturity Matter n Yes, generally long term interest rates are above short term interest rates
 Why Might we Assume that the Long Term R will be Above the Short Term n Because of the risks associated with committing one’s capital for longer periods of time: q q Uncertainty about inflation. Uncertainty about risk of default and credit ratings. Uncertainty about economic activity. Knowledge of the price (i. e. , interest rate) risk relationship regarding longer term issues.
Why Might we Assume that the Long Term R will be Above the Short Term n Because of the risks associated with committing one’s capital for longer periods of time: q q Uncertainty about inflation. Uncertainty about risk of default and credit ratings. Uncertainty about economic activity. Knowledge of the price (i. e. , interest rate) risk relationship regarding longer term issues.
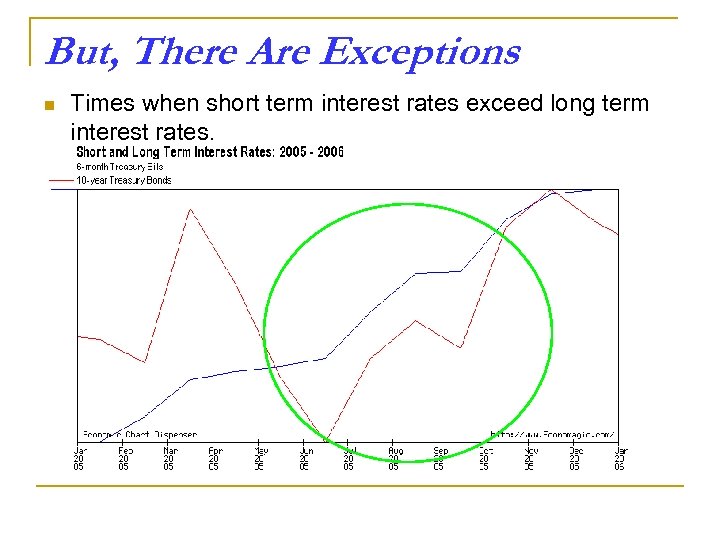 But, There Are Exceptions n Times when short term interest rates exceed long term interest rates.
But, There Are Exceptions n Times when short term interest rates exceed long term interest rates.
 Observing The Relationship between Long Ter Short Term Rates with Spreads:
Observing The Relationship between Long Ter Short Term Rates with Spreads:
 How can we Illustrate the Relationship Between Interest Rates and Maturity? n (1) We can look at interest rates over time. q Compare movements (or differentials) of long term rates to short term rates over some historical period. n n n Go back to last three (illustration) slides for examples. OR (2) We can look at interest rates at a point in time, i. e. , on a particular date. q q What is the short term interest rate, the intermediate term rate, and the long term interest rate on a specific date? This last approach is referred to as a yield curve.
How can we Illustrate the Relationship Between Interest Rates and Maturity? n (1) We can look at interest rates over time. q Compare movements (or differentials) of long term rates to short term rates over some historical period. n n n Go back to last three (illustration) slides for examples. OR (2) We can look at interest rates at a point in time, i. e. , on a particular date. q q What is the short term interest rate, the intermediate term rate, and the long term interest rate on a specific date? This last approach is referred to as a yield curve.
 Graphing a Yield Curve n A yield curve is simply a graphic presentation of the relationship of term to maturity and yields to maturity (interest rate) on a given date. To construct it we plot: q q Term to maturity on the X axis, with its Corresponding interest rate on the Y axis, or: interest rate Term to maturity →
Graphing a Yield Curve n A yield curve is simply a graphic presentation of the relationship of term to maturity and yields to maturity (interest rate) on a given date. To construct it we plot: q q Term to maturity on the X axis, with its Corresponding interest rate on the Y axis, or: interest rate Term to maturity →
 First Possible Yield Curve: Upward Sweep (Ascending, Positive) Assume following observed market interest rates: Short term (st) interest rates are 4% and Long term (lt) interest rates are 8%. Then the yield curve is upward (positive) sweeping: i rate 8% 4% o o (st) Term to Maturity (lt)
First Possible Yield Curve: Upward Sweep (Ascending, Positive) Assume following observed market interest rates: Short term (st) interest rates are 4% and Long term (lt) interest rates are 8%. Then the yield curve is upward (positive) sweeping: i rate 8% 4% o o (st) Term to Maturity (lt)
 Second Possible Yield Curve: Downward Sweep (Descending, Inverted, Negative) Assume following observed market interest rates: Short term (st) interest rates are 7% and Long term (lt) interest rates are 3% The the yield curve is downward sweeping: i rate 7% 3% o o (st) Term to Maturity (lt)
Second Possible Yield Curve: Downward Sweep (Descending, Inverted, Negative) Assume following observed market interest rates: Short term (st) interest rates are 7% and Long term (lt) interest rates are 3% The the yield curve is downward sweeping: i rate 7% 3% o o (st) Term to Maturity (lt)
 Third Possible Yield Curve: Flat Assume following observed market interest rates: Short term (st) interest rates are 7% and Long term (lt) interest rates are 7% Then the yield curve is (relatively) flat: i rate 7% o o (st) Term to Maturity (lt)
Third Possible Yield Curve: Flat Assume following observed market interest rates: Short term (st) interest rates are 7% and Long term (lt) interest rates are 7% Then the yield curve is (relatively) flat: i rate 7% o o (st) Term to Maturity (lt)
 Summary: Three Yield Curve Shapes n As illustrated in the last three slides, there are three basic shapes that yield curves can take. These are: q q q n Ascending Yield Curves (“Upward Sloping; Positive”) : Long term interest rates higher than short interest term Descending Yield Curves (“Downward Sloping; Inverted; Negative”) : Short term interest rates higher than long term interest rates. (Relatively) Flat Yield Curves: Long term and short term rates essentially the same. Next slide illustrates these three basic shapes for historical U. S. data.
Summary: Three Yield Curve Shapes n As illustrated in the last three slides, there are three basic shapes that yield curves can take. These are: q q q n Ascending Yield Curves (“Upward Sloping; Positive”) : Long term interest rates higher than short interest term Descending Yield Curves (“Downward Sloping; Inverted; Negative”) : Short term interest rates higher than long term interest rates. (Relatively) Flat Yield Curves: Long term and short term rates essentially the same. Next slide illustrates these three basic shapes for historical U. S. data.
 Historical U. S. Yield Curves
Historical U. S. Yield Curves
 Observations About Yield Curves Over Long Periods of Time n More variation (i. e. , basis point change) associated with the shorter term segment of the yield curve. n Also look at the dynamic yield curve over time: http: //stockcharts. com/freecharts/yieldcurve. html
Observations About Yield Curves Over Long Periods of Time n More variation (i. e. , basis point change) associated with the shorter term segment of the yield curve. n Also look at the dynamic yield curve over time: http: //stockcharts. com/freecharts/yieldcurve. html
 How Do We Actually Construct a Yield Curve? What Debt Instrument Should We Use? n Debt instrument possibilities include: q q q n Federal government debt, Municipal debt, or Corporate debt Recommendation: q We need to make sure that observed differences in market interest rates are not being affected by credit risk (i. e. , default risk), thus we generally use data only from Government securities n n We assume that these securities carry no risk of default. We can, however, construct non-government yield curves.
How Do We Actually Construct a Yield Curve? What Debt Instrument Should We Use? n Debt instrument possibilities include: q q q n Federal government debt, Municipal debt, or Corporate debt Recommendation: q We need to make sure that observed differences in market interest rates are not being affected by credit risk (i. e. , default risk), thus we generally use data only from Government securities n n We assume that these securities carry no risk of default. We can, however, construct non-government yield curves.
 How Do We Actually Construct a Yield Curve? Wh Interest Rate Should We Use? n Interest rate possibilities include: q q q n Coupon yield = coupon payment/par value Current yield = coupon payment/market price of bond. Yield to maturity = internal rate of return on a bond’s cash flow. Recommendation: q Use Yield to Maturity as it is the best representation of interest rate conditions at a point in time. n q q Because it takes into account the time value of money If you don’t have yield to maturity data, use the current yield as this is a better approximation of the yield to maturity than is the coupon yield Never use the coupon yield.
How Do We Actually Construct a Yield Curve? Wh Interest Rate Should We Use? n Interest rate possibilities include: q q q n Coupon yield = coupon payment/par value Current yield = coupon payment/market price of bond. Yield to maturity = internal rate of return on a bond’s cash flow. Recommendation: q Use Yield to Maturity as it is the best representation of interest rate conditions at a point in time. n q q Because it takes into account the time value of money If you don’t have yield to maturity data, use the current yield as this is a better approximation of the yield to maturity than is the coupon yield Never use the coupon yield.
 Constructing a Yield Curve Bloomberg Data: U. S. Treasuries, Feb 24, 2011 COUPON MATURITY PRICE/YIELD 3 -Month 0. 000 05/26/2011 0. 11 / 0. 12 6 -Month 0. 000 08/25/2011 0. 15 / 0. 15 12 -Month 0. 000 02/09/2012 0. 23 / 0. 23 2 -Year 0. 625 02/28/2013 99 -28+ / 0. 73 3 -Year 1. 250 02/15/2014 100 -02+ / 1. 22 5 -Year 2. 125 02/29/2016 99 -11 / 2. 18 7 -Year 2. 625 01/31/2018 98 -20+ / 2. 84 10 -Year 3. 625 02/15/2021 101 -17+ / 3. 44 30 -Year 4. 750 02/15/2041 103 -17½ / 4. 53 Construct a Yield Curve for Feb 24, 2011
Constructing a Yield Curve Bloomberg Data: U. S. Treasuries, Feb 24, 2011 COUPON MATURITY PRICE/YIELD 3 -Month 0. 000 05/26/2011 0. 11 / 0. 12 6 -Month 0. 000 08/25/2011 0. 15 / 0. 15 12 -Month 0. 000 02/09/2012 0. 23 / 0. 23 2 -Year 0. 625 02/28/2013 99 -28+ / 0. 73 3 -Year 1. 250 02/15/2014 100 -02+ / 1. 22 5 -Year 2. 125 02/29/2016 99 -11 / 2. 18 7 -Year 2. 625 01/31/2018 98 -20+ / 2. 84 10 -Year 3. 625 02/15/2021 101 -17+ / 3. 44 30 -Year 4. 750 02/15/2041 103 -17½ / 4. 53 Construct a Yield Curve for Feb 24, 2011
 Real Time Yield Curves on Line n n Visit the following sites: (1) Bloomberg: U. S. Treasury and Selected Foreign Country Yield Curves q n n (2) Dynamic U. S. Treasury Yield Curve http: //stockcharts. com/charts/yieldcurve. html q n You can view yield curve changes over time. (3)Yield Curves for Treasuries and Corporates q n http: //www. bloomberg. com/markets/rates/index. html http: //www. bondsonline. com/Todays_Market/Composit e_Bond_Yields. php (4) Nominal and Real U. S. Treasury Yield Curves q http: //www. treasury. gov/resource-center/data-chartcenter/interest-rates/Pages/Historic-Yield-Data. Visualization. aspx
Real Time Yield Curves on Line n n Visit the following sites: (1) Bloomberg: U. S. Treasury and Selected Foreign Country Yield Curves q n n (2) Dynamic U. S. Treasury Yield Curve http: //stockcharts. com/charts/yieldcurve. html q n You can view yield curve changes over time. (3)Yield Curves for Treasuries and Corporates q n http: //www. bloomberg. com/markets/rates/index. html http: //www. bondsonline. com/Todays_Market/Composit e_Bond_Yields. php (4) Nominal and Real U. S. Treasury Yield Curves q http: //www. treasury. gov/resource-center/data-chartcenter/interest-rates/Pages/Historic-Yield-Data. Visualization. aspx
 Real Time Yield Curves for Foreign Countries n United Kingdom (and U. S. ) q http: //www. yieldcurve. com/marketyieldcurve. asp n n This site lets you compare UK and US yield curves. Euro-Zone q http: //www. ecb. int/stats/money/yc/html/index. en. htm l n Note: Select “spot rate” curve for current Euro-zone yield curve
Real Time Yield Curves for Foreign Countries n United Kingdom (and U. S. ) q http: //www. yieldcurve. com/marketyieldcurve. asp n n This site lets you compare UK and US yield curves. Euro-Zone q http: //www. ecb. int/stats/money/yc/html/index. en. htm l n Note: Select “spot rate” curve for current Euro-zone yield curve
 Theories to Explain the Shape of the Yield Curve n There are three generally accepted theories or explanations of the yield curve, these are: q q q n (Pure) Expectations Theory Liquidity Premium Theory Market Segmentations Theory These theories are potentially important because they provide a framework for: q q q (1) Understanding the shape of the yield curve and (2) Forecasting future interest rates. (3) Forecasting future changes in economic activity (i. e. , business cycle turning points) n Forecasting is covered in Lecture 5, Part 2
Theories to Explain the Shape of the Yield Curve n There are three generally accepted theories or explanations of the yield curve, these are: q q q n (Pure) Expectations Theory Liquidity Premium Theory Market Segmentations Theory These theories are potentially important because they provide a framework for: q q q (1) Understanding the shape of the yield curve and (2) Forecasting future interest rates. (3) Forecasting future changes in economic activity (i. e. , business cycle turning points) n Forecasting is covered in Lecture 5, Part 2
 The (Pure) Expectations Theory n n n Assumption: Financial market’s expectations regarding future interest rates will shape the current yield curve. Model assumes that financial markets are efficient. What does this mean? q The existence of widely disseminated information allows market participants to form expectations about future interest rates (referred to as forward interest rates). q q q Forward rates are based upon the markets’ analysis of all relevant events likely to affect interest rates in the future (e. g. , central bank actions, inflationary expectations, business cycles). These forward rates are incorporated into current market interest rates (also referred to as spot interest rates). These spot interest rates are the interest rates represented in observed yield curves.
The (Pure) Expectations Theory n n n Assumption: Financial market’s expectations regarding future interest rates will shape the current yield curve. Model assumes that financial markets are efficient. What does this mean? q The existence of widely disseminated information allows market participants to form expectations about future interest rates (referred to as forward interest rates). q q q Forward rates are based upon the markets’ analysis of all relevant events likely to affect interest rates in the future (e. g. , central bank actions, inflationary expectations, business cycles). These forward rates are incorporated into current market interest rates (also referred to as spot interest rates). These spot interest rates are the interest rates represented in observed yield curves.
 The Expectations Theory: Long Term Spo Interest Rates n The Expectations Theory assumes that the current long term spot interest rate is comprised of 2 components q q n (1) current short term (i. e. , spot) interest rate and (2) expected, or forward, interest rate. Assume: q q q q (1) the current 1 year spot interest rate is 3% and (2) the forward 1 year interest rate, 1 year from now is 5%. Also, assume there is no risk of default and no required premium for longer term financial assets. Given the above, what will the market set as the current 2 year spot interest rate? Answer: 4. 0% (or 2 year spot = (3. 0 +5. 0)/2 At 4%, the markets are indifferent to investing (or lending) for 1 year or 2 years (see next slide). What if the current 1 year spot rate is 7% and the markets expect the 1 year rate, 1 year from now to be 5%
The Expectations Theory: Long Term Spo Interest Rates n The Expectations Theory assumes that the current long term spot interest rate is comprised of 2 components q q n (1) current short term (i. e. , spot) interest rate and (2) expected, or forward, interest rate. Assume: q q q q (1) the current 1 year spot interest rate is 3% and (2) the forward 1 year interest rate, 1 year from now is 5%. Also, assume there is no risk of default and no required premium for longer term financial assets. Given the above, what will the market set as the current 2 year spot interest rate? Answer: 4. 0% (or 2 year spot = (3. 0 +5. 0)/2 At 4%, the markets are indifferent to investing (or lending) for 1 year or 2 years (see next slide). What if the current 1 year spot rate is 7% and the markets expect the 1 year rate, 1 year from now to be 5%
 The Expectations Theory: Solving for the L Term Spot Interest Rate n Assumptions: q q q n n (1) the current 1 year spot interest rate is 3% and (2) the forward 1 year interest rate, 1 year from now is 5%. Also, assume there is no risk of default and no required premium for longer term financial assets. What is the 2 year spot interest rate? Answer: 4. 0% q Why? n n At 4%, the financial markets are indifferent to investing (or lending) for 1 year or 2 years. A series of 2, one year instruments will offer an average annual return or 4% and the 2 year instrument will offer an annual return of 4%
The Expectations Theory: Solving for the L Term Spot Interest Rate n Assumptions: q q q n n (1) the current 1 year spot interest rate is 3% and (2) the forward 1 year interest rate, 1 year from now is 5%. Also, assume there is no risk of default and no required premium for longer term financial assets. What is the 2 year spot interest rate? Answer: 4. 0% q Why? n n At 4%, the financial markets are indifferent to investing (or lending) for 1 year or 2 years. A series of 2, one year instruments will offer an average annual return or 4% and the 2 year instrument will offer an annual return of 4%
 Illustrating the Expectations Theory n Assume: q q n (1) it, the current 1 year spot interest rate is 3% and (2) iet+1, the forward 1 year interest rate, 1 year from now is 5%. Then: q (3) i 2 t, the current 2 year spot will equal 4%
Illustrating the Expectations Theory n Assume: q q n (1) it, the current 1 year spot interest rate is 3% and (2) iet+1, the forward 1 year interest rate, 1 year from now is 5%. Then: q (3) i 2 t, the current 2 year spot will equal 4%
 Expectations Formula for the Long-term Interest Rate Where: The current long term spot interest rate (ilsn where n = years to maturity) is equal to the average of the current short term spot rate (isst) and all appropriate expected future short term (i. e. , forward) rates (iet+1, … ien). Note: The long term spot rate (ilsn) is the observable long term market interest rate. The current short term spot rate (isst) is the observable short term market interest rate, for time period t. Forward rates (iet+1, … ien) are the market’s expectations about where interest rates will be in the future.
Expectations Formula for the Long-term Interest Rate Where: The current long term spot interest rate (ilsn where n = years to maturity) is equal to the average of the current short term spot rate (isst) and all appropriate expected future short term (i. e. , forward) rates (iet+1, … ien). Note: The long term spot rate (ilsn) is the observable long term market interest rate. The current short term spot rate (isst) is the observable short term market interest rate, for time period t. Forward rates (iet+1, … ien) are the market’s expectations about where interest rates will be in the future.
 The Market’s Setting of Long Term Spot Rates: Example 1 n Assume the following: q Current (spot) one year rate is 5% and q The market’s forward one year rates over the next five years (years 2, 3, 4, and 5) are: n n n Beginning of year 2: 6%, Beginning of year 3: 7%, Beginning of year 4: 8%, and Beginning of year 5: 9%. Given this data, calculate the following long term spot rates: q q Current (spot) two year bond rate (ils 2) Current (spot) five year bond rate (ils 5)
The Market’s Setting of Long Term Spot Rates: Example 1 n Assume the following: q Current (spot) one year rate is 5% and q The market’s forward one year rates over the next five years (years 2, 3, 4, and 5) are: n n n Beginning of year 2: 6%, Beginning of year 3: 7%, Beginning of year 4: 8%, and Beginning of year 5: 9%. Given this data, calculate the following long term spot rates: q q Current (spot) two year bond rate (ils 2) Current (spot) five year bond rate (ils 5)
 Market’s Long Term Spot Rates n 2 Year Interest Rate: The market’s current rate on a two-year bond is calculated as follows: q q n Current (spot)1 year rate is 5% and forward 1 year rate, 1 year from now is 6%, then: Current 2 year bond rate = (5% + 6%)/2 = 5. 5% 5 year Interest Rate: The market’s current rate on a five-year bond is calculated as follows: q q Current (spot)1 year rate is 5% and forward 1 year rates, 1 year from now through five years from now are: 6%, 7%, 8%, and 9%, then: Current 5 year bond rate = (5% + 6% + 7% + 8% + 9%)/5 = 7%
Market’s Long Term Spot Rates n 2 Year Interest Rate: The market’s current rate on a two-year bond is calculated as follows: q q n Current (spot)1 year rate is 5% and forward 1 year rate, 1 year from now is 6%, then: Current 2 year bond rate = (5% + 6%)/2 = 5. 5% 5 year Interest Rate: The market’s current rate on a five-year bond is calculated as follows: q q Current (spot)1 year rate is 5% and forward 1 year rates, 1 year from now through five years from now are: 6%, 7%, 8%, and 9%, then: Current 5 year bond rate = (5% + 6% + 7% + 8% + 9%)/5 = 7%
 Expectations For Rising Interest Rates and the Observed Yield Curve n If interest rates are expected to rise in future, forward rates will be above today's spot rates. q q q The higher forward rates will result in higher observed spot rates. Recall previous example: The current (spot)1 year rate was 5% and forward 1 year rate, 1 year from now was 6%. n n The forward rate is higher because the market expects higher rates in the future Question: Given this situation where forward rates are higher than current spot rate (because the market expects higher rates in the future), what will the current yield curve look like?
Expectations For Rising Interest Rates and the Observed Yield Curve n If interest rates are expected to rise in future, forward rates will be above today's spot rates. q q q The higher forward rates will result in higher observed spot rates. Recall previous example: The current (spot)1 year rate was 5% and forward 1 year rate, 1 year from now was 6%. n n The forward rate is higher because the market expects higher rates in the future Question: Given this situation where forward rates are higher than current spot rate (because the market expects higher rates in the future), what will the current yield curve look like?
 Yield Curve When Market Expects Higher Interest Rates in the Future n q If the current 1 year spot rate (S 1) is 5. 0% and Forward 1 year rates are: n n if 2 = 6%, if 3 = 7%, If 4 = 8% If 5 = 9% Then observed long term spot rates are: n n n q Spot 2 year (S 2) = 5. 5% Spot 3 year (S 3) = 6. 0% Spot 4 year (S 4) = 6. 5% Spot 5 year (S 5) = 7. 0% Conclusion: The observed yield curve is upward sloping because the market expects higher interest rates in the future. Spot interest rate 9. 0% oif 5 8. 0 oif 4 7. 5 7. 0 oif 3 os 5 6. 5 Os 4 6. 0 oif 2 Os 3 5. 5 os 2 5. 0 os 1 1 2 3 4 5 year Term to Maturity →
Yield Curve When Market Expects Higher Interest Rates in the Future n q If the current 1 year spot rate (S 1) is 5. 0% and Forward 1 year rates are: n n if 2 = 6%, if 3 = 7%, If 4 = 8% If 5 = 9% Then observed long term spot rates are: n n n q Spot 2 year (S 2) = 5. 5% Spot 3 year (S 3) = 6. 0% Spot 4 year (S 4) = 6. 5% Spot 5 year (S 5) = 7. 0% Conclusion: The observed yield curve is upward sloping because the market expects higher interest rates in the future. Spot interest rate 9. 0% oif 5 8. 0 oif 4 7. 5 7. 0 oif 3 os 5 6. 5 Os 4 6. 0 oif 2 Os 3 5. 5 os 2 5. 0 os 1 1 2 3 4 5 year Term to Maturity →
 Expectations For Falling Interest Rates and the Observed Yield Curve n If interest rates are expected to fall in future, forward rates will be below today's spot rates. q q Assume: The current (spot)1 year rate is 9% and forward 1 year rate, 1 year from now is 8% q Calculate the 2 year spot rate: q Answer: Current 2 year bond rate = (9% + 8%)/2 = 8. 5% n n Thus, lower forward rates result in lower observed spot rate. Question: Given this situation where forward rates are lower than current spot rate (because the market expects lower rates in the future), what will the current yield curve look like?
Expectations For Falling Interest Rates and the Observed Yield Curve n If interest rates are expected to fall in future, forward rates will be below today's spot rates. q q Assume: The current (spot)1 year rate is 9% and forward 1 year rate, 1 year from now is 8% q Calculate the 2 year spot rate: q Answer: Current 2 year bond rate = (9% + 8%)/2 = 8. 5% n n Thus, lower forward rates result in lower observed spot rate. Question: Given this situation where forward rates are lower than current spot rate (because the market expects lower rates in the future), what will the current yield curve look like?
 Yield Curve When Market Expects Lowe Interest Rates in the Future If the current 1 year spot rate (S 1) is 9%, and : q Forward 1 year rates are: n n n q Then observed long term spot rates are: n n n if 2 = 8%, if 3 = 7%, If 4 = 6% If 5 = 5% Spot 2 year (S 2) = 8. 5% Spot 3 year (S 3) = 8. 0% Spot 4 year (S 4) = 7. 5% Spot 5 year (S 5) = 7. 0% Conclusion: The observed yield curve is downward sloping because the market expects lower interest rates in the future. Spot interest rate 9. 0% o. S 1 8. 5 o. S 2 8. 0 oif 2 Os 3 7. 5 os 4 7. 0 oif 3 os 5 6. 0 oif 4 5. 5 5. 0 oif 5 1 2 3 4 5 year Term to Maturity →
Yield Curve When Market Expects Lowe Interest Rates in the Future If the current 1 year spot rate (S 1) is 9%, and : q Forward 1 year rates are: n n n q Then observed long term spot rates are: n n n if 2 = 8%, if 3 = 7%, If 4 = 6% If 5 = 5% Spot 2 year (S 2) = 8. 5% Spot 3 year (S 3) = 8. 0% Spot 4 year (S 4) = 7. 5% Spot 5 year (S 5) = 7. 0% Conclusion: The observed yield curve is downward sloping because the market expects lower interest rates in the future. Spot interest rate 9. 0% o. S 1 8. 5 o. S 2 8. 0 oif 2 Os 3 7. 5 os 4 7. 0 oif 3 os 5 6. 0 oif 4 5. 5 5. 0 oif 5 1 2 3 4 5 year Term to Maturity →
 Yield Curve When Market Expects No Chang in Interest Rates in the Future If the current 1 year spot rate (S 1) is 7%, and : q Forward 1 year rates are: n n n q Then observed long term spot rates are: n n n if 2 = 7%, if 3 = 7%, If 4 = 7% If 5 = 7% Spot 2 year (S 2) = 7. 0% Spot 3 year (S 3) = 7. 0% Spot 4 year (S 4) = 7. 0% Spot 5 year (S 5) = 7. 0% Conclusion: The observed yield curve is flat because the market expects no change in interest rates in the future. Spot interest rate 7. 5% 7. 0 os 1 6. 5 1 oei 2 oie 3 oie 4 os 5 2 3 4 5 year Term to Maturity →
Yield Curve When Market Expects No Chang in Interest Rates in the Future If the current 1 year spot rate (S 1) is 7%, and : q Forward 1 year rates are: n n n q Then observed long term spot rates are: n n n if 2 = 7%, if 3 = 7%, If 4 = 7% If 5 = 7% Spot 2 year (S 2) = 7. 0% Spot 3 year (S 3) = 7. 0% Spot 4 year (S 4) = 7. 0% Spot 5 year (S 5) = 7. 0% Conclusion: The observed yield curve is flat because the market expects no change in interest rates in the future. Spot interest rate 7. 5% 7. 0 os 1 6. 5 1 oei 2 oie 3 oie 4 os 5 2 3 4 5 year Term to Maturity →
 Summary of Expectations Regarding Futu Interest Rates n The shape and slope of the yield curve reflects the markets’ expectations about future interest rates. q Upward Sloping (Ascending, Positive) Yield Curves: n Future (forward) interest rates are expected to increase above existing spot rates. q Downward Sloping (Descending, Inverted, Negative) Yield Curves: n Future (forward) interest rates are expected to decrease below existing spot rates. q Flat Yield Curves n Future (forward) interest rates are expected to remain the same as existing spot rates.
Summary of Expectations Regarding Futu Interest Rates n The shape and slope of the yield curve reflects the markets’ expectations about future interest rates. q Upward Sloping (Ascending, Positive) Yield Curves: n Future (forward) interest rates are expected to increase above existing spot rates. q Downward Sloping (Descending, Inverted, Negative) Yield Curves: n Future (forward) interest rates are expected to decrease below existing spot rates. q Flat Yield Curves n Future (forward) interest rates are expected to remain the same as existing spot rates.
 Liquidity Premium Theory n n n The second explanation of the yield curve is referred to as the Liquidity Premium Theory. Assumptions of Liquidity Premium Theory: Long term securities carry a greater risk and therefore investors require greater returns to invest for longer periods of time. What are these risks associated with longer term securities: q q Price risk (i. e. , interest rate risk). Risk of default (on corporate issues).
Liquidity Premium Theory n n n The second explanation of the yield curve is referred to as the Liquidity Premium Theory. Assumptions of Liquidity Premium Theory: Long term securities carry a greater risk and therefore investors require greater returns to invest for longer periods of time. What are these risks associated with longer term securities: q q Price risk (i. e. , interest rate risk). Risk of default (on corporate issues).
 Liquidity Premium n Liquidity Premium is added by market participants to longer term bonds. q n It is actually a premium for giving up the liquidity associated with shorter term issues. Thus, if observed long term rates are higher than short term rates, the question is: q q q Are higher long term interest rates due to expectations of higher interest rates in the future (i. e. , the Expectations Theory), OR Are higher long term interest rates due to liquidity premiums (i. e. , the Liquidity Premium Theory), OR Some combination of both of the above?
Liquidity Premium n Liquidity Premium is added by market participants to longer term bonds. q n It is actually a premium for giving up the liquidity associated with shorter term issues. Thus, if observed long term rates are higher than short term rates, the question is: q q q Are higher long term interest rates due to expectations of higher interest rates in the future (i. e. , the Expectations Theory), OR Are higher long term interest rates due to liquidity premiums (i. e. , the Liquidity Premium Theory), OR Some combination of both of the above?
 Liquidity Premium Theory Formula for Lo Term Interest Rates n The Liquidity Premium needs to modify the pure expectations theory formula to take into account a liquidity premium, or n Where, Ln is the liquidity premium for holding a bond of n maturity.
Liquidity Premium Theory Formula for Lo Term Interest Rates n The Liquidity Premium needs to modify the pure expectations theory formula to take into account a liquidity premium, or n Where, Ln is the liquidity premium for holding a bond of n maturity.
 Liquidity Premium Example n Assume: One-year (spot and forward) interest rates over the next five years as follows: q q 1 year spot interest rate = 5% 1 year forward rates: n n n Now assume investors' liquidity premiums for holding one- to five-year bonds as follows: q q q n 1 year bond = 0. 00% 2 year bonds = 0. 25% 3 year bonds = 0. 50%, 4 year bonds = 0. 75%, and 5 year bonds = 1. 00% With this information, calculate the market interest rate on: q q n Beginning year 2 = 6%, Beginning year 3 = 7%, Beginning year 4 = 8%, and Beginning year 5 = 9% 1) a two year bond (with a Ln =. 25%) 2) a five year bond (with a Ln = 1. 0%) And, compare these calculated long term rates with those for the pure expectations theory formula.
Liquidity Premium Example n Assume: One-year (spot and forward) interest rates over the next five years as follows: q q 1 year spot interest rate = 5% 1 year forward rates: n n n Now assume investors' liquidity premiums for holding one- to five-year bonds as follows: q q q n 1 year bond = 0. 00% 2 year bonds = 0. 25% 3 year bonds = 0. 50%, 4 year bonds = 0. 75%, and 5 year bonds = 1. 00% With this information, calculate the market interest rate on: q q n Beginning year 2 = 6%, Beginning year 3 = 7%, Beginning year 4 = 8%, and Beginning year 5 = 9% 1) a two year bond (with a Ln =. 25%) 2) a five year bond (with a Ln = 1. 0%) And, compare these calculated long term rates with those for the pure expectations theory formula.
 Calculation of Spot Interest Rates With Liquidity Premium n n n Market interest rate on the two-year bond with a liquidity premium on. 25% on a 2 year bond: (5% + 6%)/2 + 0. 25% = 5. 75% Market interest rate on the five-year bond with a liquidity premium of 1. 0% on a five year bond: (5% + 6% + 7% + 8% + 9%)/5 + 1. 0% = 8% Compare Liquidity Premium spot rates to Expectations spot rates: q q n 2 year spot rate: 5. 75% (Liquidity Premium); 5. 5% (Expectations) 5 year spot rate: 8. 00% (Liquidity Premium); 7. 0% (Expectations) As you can see: q The liquidity premium theory produces yield curves more steeply upward sloping.
Calculation of Spot Interest Rates With Liquidity Premium n n n Market interest rate on the two-year bond with a liquidity premium on. 25% on a 2 year bond: (5% + 6%)/2 + 0. 25% = 5. 75% Market interest rate on the five-year bond with a liquidity premium of 1. 0% on a five year bond: (5% + 6% + 7% + 8% + 9%)/5 + 1. 0% = 8% Compare Liquidity Premium spot rates to Expectations spot rates: q q n 2 year spot rate: 5. 75% (Liquidity Premium); 5. 5% (Expectations) 5 year spot rate: 8. 00% (Liquidity Premium); 7. 0% (Expectations) As you can see: q The liquidity premium theory produces yield curves more steeply upward sloping.
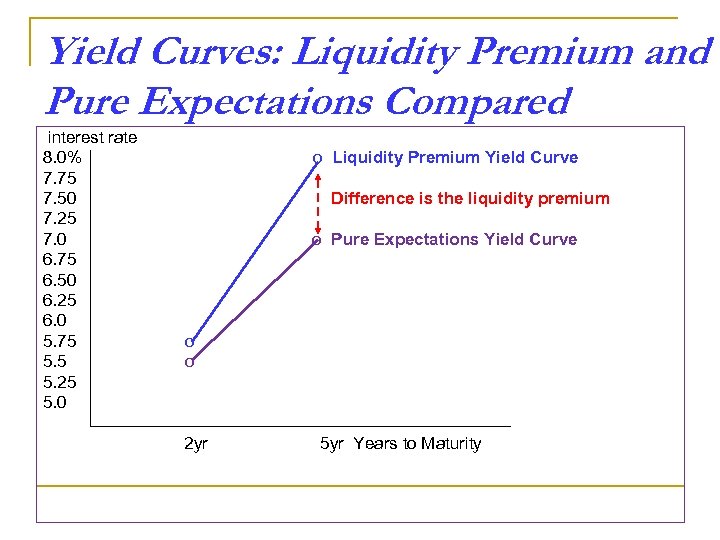 Yield Curves: Liquidity Premium and Pure Expectations Compared interest rate 8. 0% 7. 75 7. 50 7. 25 7. 0 6. 75 6. 50 6. 25 6. 0 5. 75 5. 25 5. 0 o Liquidity Premium Yield Curve Difference is the liquidity premium o Pure Expectations Yield Curve o o 2 yr 5 yr Years to Maturity
Yield Curves: Liquidity Premium and Pure Expectations Compared interest rate 8. 0% 7. 75 7. 50 7. 25 7. 0 6. 75 6. 50 6. 25 6. 0 5. 75 5. 25 5. 0 o Liquidity Premium Yield Curve Difference is the liquidity premium o Pure Expectations Yield Curve o o 2 yr 5 yr Years to Maturity
 Liquidity Premium Example When Interest Rates are Expected to Fall n Assume: One-year (spot and forward) interest rates over the next five years as follows: q q 1 year spot interest rate = 5% 1 year forward rates: n n n Now assume investors' liquidity premiums for holding one- to five-year bonds as follows: q q q n 1 year bond = 0. 00% 2 year bonds = 0. 25% 3 year bonds = 0. 50%, 4 year bonds = 0. 75%, and 5 year bonds = 1. 00% With this information, calculate the market interest rate on: q q n Beginning year 2 = 4%, Beginning year 3 = 3%, Beginning year 4 = 2%, and Beginning year 5 = 1% 1) a two year bond (with a Ln =. 25%) 2) a five year bond (with a Ln = 1. 0%) And, compare these calculated long term rates with those for the pure expectations theory formula.
Liquidity Premium Example When Interest Rates are Expected to Fall n Assume: One-year (spot and forward) interest rates over the next five years as follows: q q 1 year spot interest rate = 5% 1 year forward rates: n n n Now assume investors' liquidity premiums for holding one- to five-year bonds as follows: q q q n 1 year bond = 0. 00% 2 year bonds = 0. 25% 3 year bonds = 0. 50%, 4 year bonds = 0. 75%, and 5 year bonds = 1. 00% With this information, calculate the market interest rate on: q q n Beginning year 2 = 4%, Beginning year 3 = 3%, Beginning year 4 = 2%, and Beginning year 5 = 1% 1) a two year bond (with a Ln =. 25%) 2) a five year bond (with a Ln = 1. 0%) And, compare these calculated long term rates with those for the pure expectations theory formula.
 Calculation of Spot Interest Rates With Liquidity Premium n n n Market interest rate on the two-year bond with a liquidity premium on. 25% on a 2 year bond: (5% + 4%)/2 + 0. 25% = 4. 50 + 0. 25 = 4. 75% Market interest rate on the five-year bond with a liquidity premium of 1. 0% on a five year bond: (5% + 4% + 3% + 2% + 1%)/5 + 1. 0% = 3. 0 + 1. 0 = 4% Compare Liquidity Premium spot rates to Expectations spot rates: q q n 2 year spot rate: 4. 75% (Liquidity Premium); 4. 5% (Expectations) 5 year spot rate: 4. 00% (Liquidity Premium); 3. 0% (Expectations) As you can see: q The liquidity premium theory produces yield curves less inverted.
Calculation of Spot Interest Rates With Liquidity Premium n n n Market interest rate on the two-year bond with a liquidity premium on. 25% on a 2 year bond: (5% + 4%)/2 + 0. 25% = 4. 50 + 0. 25 = 4. 75% Market interest rate on the five-year bond with a liquidity premium of 1. 0% on a five year bond: (5% + 4% + 3% + 2% + 1%)/5 + 1. 0% = 3. 0 + 1. 0 = 4% Compare Liquidity Premium spot rates to Expectations spot rates: q q n 2 year spot rate: 4. 75% (Liquidity Premium); 4. 5% (Expectations) 5 year spot rate: 4. 00% (Liquidity Premium); 3. 0% (Expectations) As you can see: q The liquidity premium theory produces yield curves less inverted.
 Yield Curves: Liquidity Premium and Pure Expectations Compared interest rate 5. 0% 4. 75 4. 50 4. 25 4. 00 3. 75 3. 50 3. 25 3. 0 Liquidity Premium Yield Curve Difference is the liquidity premium Pure Expectations Yield Curve 2 yr 5 yr Years to Maturity
Yield Curves: Liquidity Premium and Pure Expectations Compared interest rate 5. 0% 4. 75 4. 50 4. 25 4. 00 3. 75 3. 50 3. 25 3. 0 Liquidity Premium Yield Curve Difference is the liquidity premium Pure Expectations Yield Curve 2 yr 5 yr Years to Maturity
 Market Segmentations Theory n The third theory of the yield curve is the Market Segmentations Theory. n Assumptions of the Market Segmentations Theory: Each maturity segment of the yield curve (short term through long term) has its interest rate determined by the supply of and the demand for debt instruments within that maturity segment. q q Thus, within the short segment, there will be a demand supply schedule for debt instruments, and in the intermediate term and long term segments there will also be demand supply schedules. These schedules are independent of one another.
Market Segmentations Theory n The third theory of the yield curve is the Market Segmentations Theory. n Assumptions of the Market Segmentations Theory: Each maturity segment of the yield curve (short term through long term) has its interest rate determined by the supply of and the demand for debt instruments within that maturity segment. q q Thus, within the short segment, there will be a demand supply schedule for debt instruments, and in the intermediate term and long term segments there will also be demand supply schedules. These schedules are independent of one another.
 Market Segmentations Theory n n The Market Segmentations Theory begins with a determination of a “typical” yield curve, based on: What would be the typical tendencies, or preferences, of borrowers and lenders? q Question: In which maturity segment would borrowers prefer to borrow? n q Question: In which maturity segment would lenders prefer to lend (or invest)? n n Answer: Borrowers would prefer to issue (i. e. , supply) longer term debt instruments to lock in interest rate obligations. Answer: Lenders prefer to buy (i. e. , demand) shorter term debt instruments to avoid longer term risk issues. Question: What type (i. e. , shape) of yield curve would these typical tendencies produce?
Market Segmentations Theory n n The Market Segmentations Theory begins with a determination of a “typical” yield curve, based on: What would be the typical tendencies, or preferences, of borrowers and lenders? q Question: In which maturity segment would borrowers prefer to borrow? n q Question: In which maturity segment would lenders prefer to lend (or invest)? n n Answer: Borrowers would prefer to issue (i. e. , supply) longer term debt instruments to lock in interest rate obligations. Answer: Lenders prefer to buy (i. e. , demand) shorter term debt instruments to avoid longer term risk issues. Question: What type (i. e. , shape) of yield curve would these typical tendencies produce?
 Typical Upward Sweeping Market Segmentations Yield Curve Spot interest rate Lenders demanding short term debt instruments (result: pushes up price and pushes down short term interest rates) o o Borrowers supplying long term debt instruments (result: pushes down price and pushes up long term interest rates) (short term) Term to Maturity (long term)
Typical Upward Sweeping Market Segmentations Yield Curve Spot interest rate Lenders demanding short term debt instruments (result: pushes up price and pushes down short term interest rates) o o Borrowers supplying long term debt instruments (result: pushes down price and pushes up long term interest rates) (short term) Term to Maturity (long term)
 Market Segmentations Theory and the Shape of the Yield Curve n According to the market segmentations theory, the shape of the yield curve is determined by shifts in the demand for and supply of debt instruments along various segments of the maturity range. q n Model starts with a typical yield curve, which is assumed to be upward sloping. Changes in this curve reflect changes in demand supply as borrowers and lenders move away from their typical preferences.
Market Segmentations Theory and the Shape of the Yield Curve n According to the market segmentations theory, the shape of the yield curve is determined by shifts in the demand for and supply of debt instruments along various segments of the maturity range. q n Model starts with a typical yield curve, which is assumed to be upward sloping. Changes in this curve reflect changes in demand supply as borrowers and lenders move away from their typical preferences.
 Shift in the Yield Curve Under the Market Segmentations Theory Shift from typical to inverted yield curve Explanation n Borrowers shifted to the short term q Typical (Upward) Yield Curve Now a preference for issuing short term securities. n n Lenders shifted to the long term q Now a preference for demanding long term securities. n n Pushes down prices and pushes up interest rates Pushes up prices and pushes down interest rates Why might this shift in preference occur?
Shift in the Yield Curve Under the Market Segmentations Theory Shift from typical to inverted yield curve Explanation n Borrowers shifted to the short term q Typical (Upward) Yield Curve Now a preference for issuing short term securities. n n Lenders shifted to the long term q Now a preference for demanding long term securities. n n Pushes down prices and pushes up interest rates Pushes up prices and pushes down interest rates Why might this shift in preference occur?
