Fluids Your Comments Everything is going great

Fluids

Your Comments Everything is going great. It seems like there is homework due and we haven’t gone over any problems like it yet, but you do a good job of going over problems like that and help us with the homework. Just am curious how im doing in the class with regard to test grades I’m very far behind with my homework I like working problems in class. The assignments and preflights seem a little tedious when I have a ton of stuff to do. Tough stuff Keep smilin This class is very interesting, we do fun hands on stuff, but all the equations make it so much less fun Woohoo class! We’re almost done! I would appreciate more examples I feel a little confused when doing homeworks

Comments Continued One thing in particular. . . Due to the load of work we have in this class, and the pace that we continuously work at, it would be nice to know where we're at as far as grades go. Being a student in college, I TOTALLY understand what it feels like to be bogged down, and completely swamped. Next time around for this class, instead of assigning so much "busy work" that highly influences our grade, maybe drop it down a notch so we can know what we're getting in the class on a more consistent basis. Less to grade usually means faster and more efficient grading right? For me, its just hard to judge how I'm doing right now because there aren't any grades up, and the semester is creeping up quick. PLUS if the grades are coming back faster, not only do i know if i get the points or not, i can get feedback as to whether or not I'm doing the work right. I do the homework how I think it should be done, but I'm not sure whether its right or not. Thanks for putting up with us!

Pascal’s Principle • A change in pressure at any point in a confined fluid is transmitted everywhere in the fluid. • Hydraulic Lift DP 1 = DP 2 F 1/A 1 = F 2 / A 2 F 1 = F 2 (A 1/A 2) • Compare the work done by F 1 with the work done by F 2 A) W 1 > W 2 B) W 1 = W 2 (A / A ) C) W 1 < W 2 =F d W = F d cos q W 1 = F 1 d 1 = F 2 (A 1 / A 2) d 1 2 = F 2 V 1 / A 2 = F 2 d 2 = W 2 1

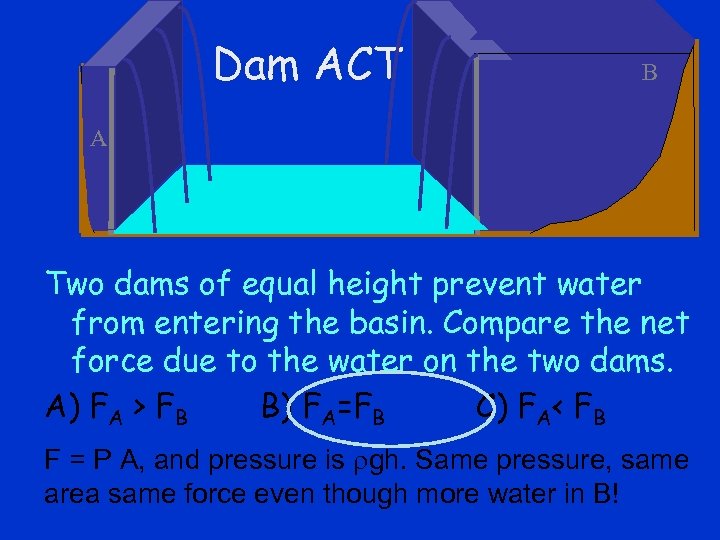Dam ACT B A A Two dams of equal height prevent water from entering the basin. Compare the net force due to the water on the two dams. A) FA > FB B) FA=FB C) FA< FB F = P A, and pressure is gh. Same pressure, same area same force even though more water in B!

Pressure and Depth Barometer: a way to measure atmospheric pressure For non-moving fluids, pressure depends only on depth. p 1=0 p 2 = p 1 + gh Patm - 0 = gh p 2=patm Measure h, determine patm example--Mercury = 13, 600 kg/m 3 patm = 1. 05 x 105 Pa h = 0. 757 m = 757 mm = 29. 80” (for 1 atm) h

Preflight Is it possible to stand on the roof of a five story (50 foot) tall house and drink, using a straw, from a glass on the ground? p=0 81% 1. No pa h 19% 2. Yes Even if the person were able to remove all the air from the straw, the height to which the outside air pressure moves the water up the straw would not be high enough for the person to drink the water. Why not? A straw is a straw. I never heard of it not working. It would be much more difficult since atmospheric pressure is no longer pushing the fluid upwards.

Archimedes’ Principle • Determine force of fluid on immersed cube – Draw FBD • FB = F 2 – F 1 = P 2 A – P 1 A • = (P 2 – P 1)A • • = gd. A • = g. V • Buoyant force is weight of displaced fluid!

Archimedes Example A cube of plastic 4. 0 cm on a side with density = 0. 8 g/cm 3 is floating in the water. When a 9 gram coin is placed on the block, how much does it sink below the water surface? SF=ma Fb – Mg – mg = 0 g Vdisp = (M+m) / h A = (M+m) / h = (M + m)/ ( A) = (51. 2+9)/(1 x 4) = 3. 76 cm Fb Mg mg h M = plastic Vcube = 4 x 4 x 4 x 0. 8 = 51. 2 g

Archimedes’ Principle • Buoyant Force (FB) – – – weight of fluid displaced FB = fluid. Voldisplaced g Fg = mg = object Volobject g object sinks if object > fluid object floats if object < fluid • If object floats… – FB = F g – Therefore: fluid g Voldispl. = object g Volobject – Therefore: Voldispl. /Volobject = object / fluid

Preflight 2 Which weighs more: 1. A large bathtub filled to the brim with water. 2. A large bathtub filled to the brim with water with a battle-ship floating in it. Tub of water + ship CORRECT 3. They will weigh the same. Tub of water Weight of ship = Buoyant force = Weight of displaced water Overflowed water

Continuity of Fluid Flow • Watch “plug” of fluid moving through the narrow part of the tube (A 1) • Time for “plug” to pass point Dt = x 1 / v 1 • Mass of fluid in “plug” m 1 = Vol 1 = A 1 x 1 or m 1 = A 1 v 1 Dt • Watch “plug” of fluid moving through the wide part of the tube (A 2) • Time for “plug” to pass point Dt = x 2 / v 2 • Mass of fluid in “plug” m 2 = Vol 2 = A 2 x 2 or m 2 = A 2 v 2 Dt • Continuity Equation says m 1 = m 2 fluid isn’t building up or disappearing • A 1 v 1 = A 2 v 2

Faucet Preflight A stream of water gets narrower as it falls from a faucet (try it & see). Explain this phenomenon using the V 1 equation of continuity A 1 A 2 V 2 As the water falls, its velocity is increasing. Since the continuity equations states that if density doesn't change. . . Area 1*velocity 1=Area 2*velocity 2. From this equation, we can say that as the velocity of the water increases, its area is going to decrease I tried to do this experiment and my roommate yelled at me for raising the water bill. Adhesion and cohesion…

Fluid Flow Concepts r A 1 P 1 v 1 A 2 P 2 v 2 • Mass flow rate: Av (kg/s) • Volume flow rate: Av (m 3/s) • Continuity: A 1 v 1 = A 2 v 2 i. e. , mass flow rate the same everywhere e. g. , flow of river

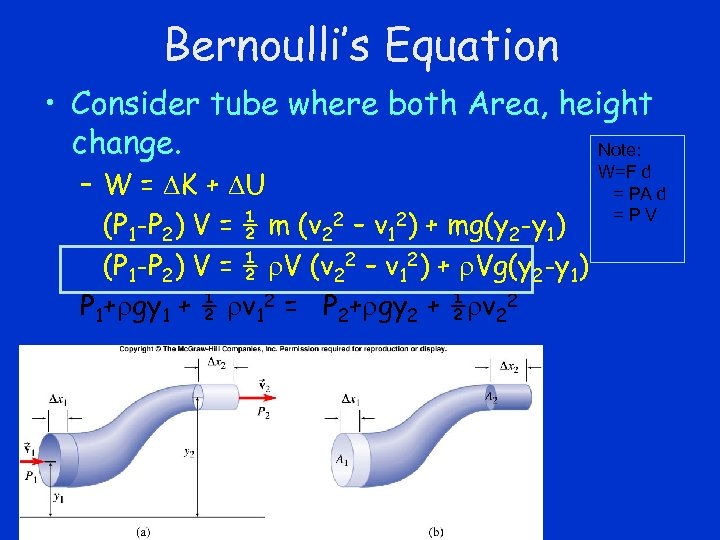Bernoulli’s Equation • Consider tube where both Area, height change. Note: – W = DK + DU (P 1 -P 2) V = ½ m (v 22 – v 12) + mg(y 2 -y 1) (P 1 -P 2) V = ½ V (v 22 – v 12) + Vg(y 2 -y 1) P 1+ gy 1 + ½ v 12 = P 2+ gy 2 + ½ v 22 W=F d = PA d =PV

Lift a House Calculate the net lift on a 15 m x 15 m house when a 30 m/s wind (1. 29 kg/m 3) blows over the top. P 1+ gy 1 + ½ v 12 = P 2+ gy 2 + ½ v 22 P 1 – P 2 = ½ (v 22 – v 12) = ½ (1. 29) (302) N / m 2 = 581 N/ m 2 F=PA = 581 N/ m 2 (15 m) = 131, 000 N = 29, 000 pounds! (note roof weighs 15, 000 lbs)

Fluid Flow Summary r A 1 P 1 v 1 • • A 2 P 2 v 2 Mass flow rate: Av (kg/s) Volume flow rate: Av (m 3/s) Continuity: A 1 v 1 = A 2 v 2 Bernoulli: P 1 + 1/2 v 12 + gh 1 = P 2 + 1/2 v 22 + gh 2