Floating Point Analysis Using Dyninst Mike Lam University

Floating Point Analysis Using Dyninst Mike Lam University of Maryland, College Park Jeff Hollingsworth, Advisor

Background • Floating point represents real numbers as (± sgnf × 2 exp) o Sign bit o Exponent o Significand (“mantissa” or “fraction”) 32 16 8 4 0 IEEE Single Exponent (8 bits) 64 32 Significand (23 bits) 16 8 4 0 IEEE Double Exponent (11 bits) Significand (52 bits) • Finite precision o Single-precision: 24 bits (~7 decimal digits) o Double-precision: 53 bits (~16 decimal digits) 2

Motivation • Finite precision causes round-off error o Compromises certain calculations o Hard to detect and diagnose • Increasingly important as HPC scales o Computation on streaming processors is faster in single precision o Data movement in double precision is a bottleneck o Need to balance speed (singles) and accuracy (doubles) 3

Our Goal Automated analysis techniques to inform developers about floating point behavior and make recommendations regarding the use of floating point arithmetic. 4

Framework CRAFT: Configurable Runtime Analysis for Floating-point Tuning • Static binary instrumentation o Read configuration settings o Replace floating-point instructions with new code o Rewrite modified binary • Dynamic analysis o Run modified program on representative data set o Produce results and recommendations 5

Previous Work • Cancellation detection o Reports loss of precision due to subtraction o Paper appeared in WHIST‘ 11 • Range tracking o Reports min/max values • Replacement o Implements mixed-precision configurations o Paper to appear in ICS’ 13 6

Mixed Precision • Use double precision where necessary • Use single precision everywhere else • Can be difficult to implement 1: LU ← PA 2: solve Ly = Pb 3: solve Ux 0 = y 4: for k = 1, 2, . . . do 5: rk ← b – Axk-1 6: solve Ly = Prk 7: solve Uzk = y 8: xk ← xk-1 + zk 9: check for convergence 10: end for Mixed-precision linear solver algorithm Red text indicates steps performed in double-precision (all other steps are single-precision) 7

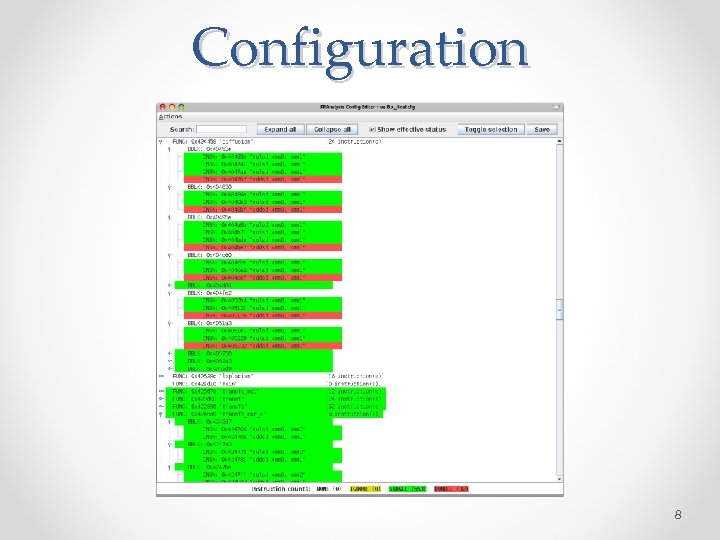Configuration 8

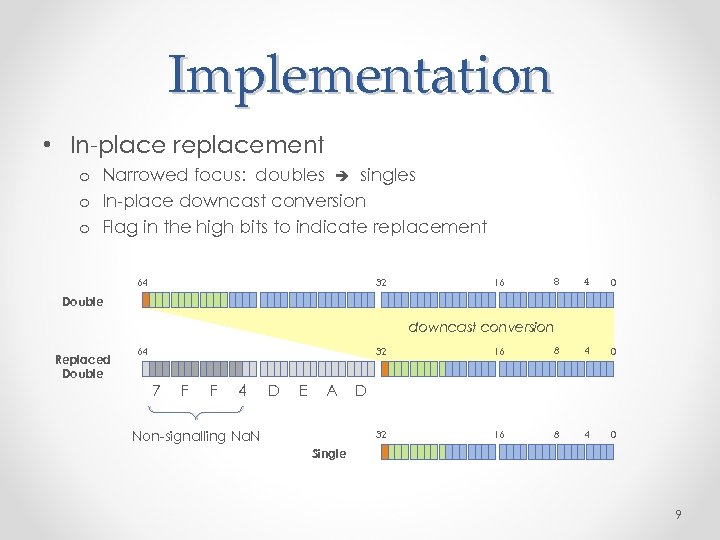Implementation • In-place replacement o Narrowed focus: doubles singles o In-place downcast conversion o Flag in the high bits to indicate replacement 64 32 16 8 4 0 Double downcast conversion Replaced Double 32 7 F F 4 D E A Non-signalling Na. N 16 8 4 0 32 64 16 8 4 0 D Single 9

Example gvec[i, j] = gvec[i, j] * lvec[3] + gvar 1 movsd 0 x 601 e 38(%rax, %rbx, 8) %xmm 0 2 mulsd -0 x 78(%rsp) %xmm 0 3 addsd -0 x 4 f 02(%rip) %xmm 0 4 movsd %xmm 0 0 x 601 e 38(%rax, %rbx, 8) 10

Example gvec[i, j] = gvec[i, j] * lvec[3] + gvar 1 3 movsd 0 x 601 e 38(%rax, %rbx, 8) %xmm 0 check/replace -0 x 78(%rsp) and %xmm 0 mulss -0 x 78(%rsp) %xmm 0 check/replace -0 x 4 f 02(%rip) and %xmm 0 addss -0 x 20 dd 43(%rip) %xmm 0 4 movsd %xmm 0 0 x 601 e 38(%rax, %rbx, 8) 2 11

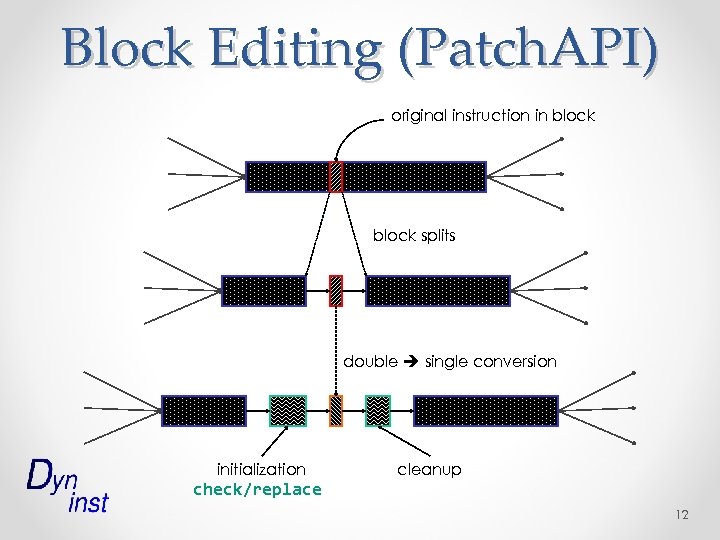Block Editing (Patch. API) original instruction in block splits double single conversion initialization check/replace cleanup 12

Automated Search • Manual mixed-precision analysis o Hard to use without intuition regarding potential replacements • Automatic mixed-precision analysis o Try lots of configurations (empirical auto-tuning) o Test with user-defined verification routine and data set o Exploit program control structure: replace larger structures (modules, functions) first o If coarse-grained replacements fail, try finer-grained subcomponent replacements 13

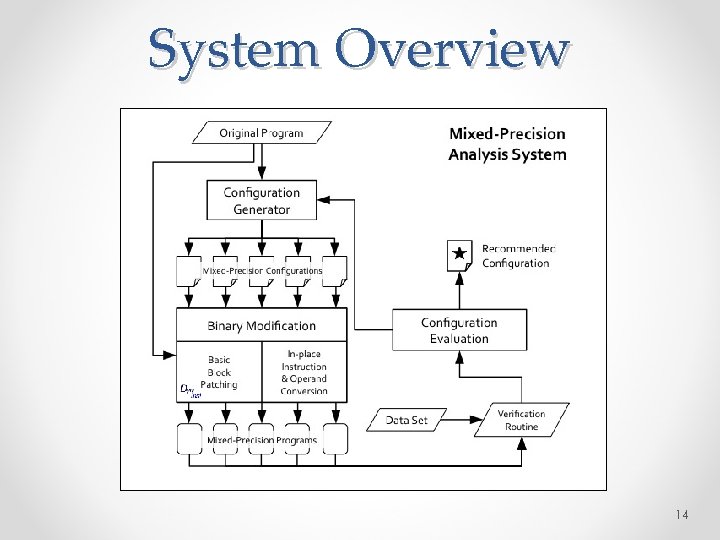System Overview 14

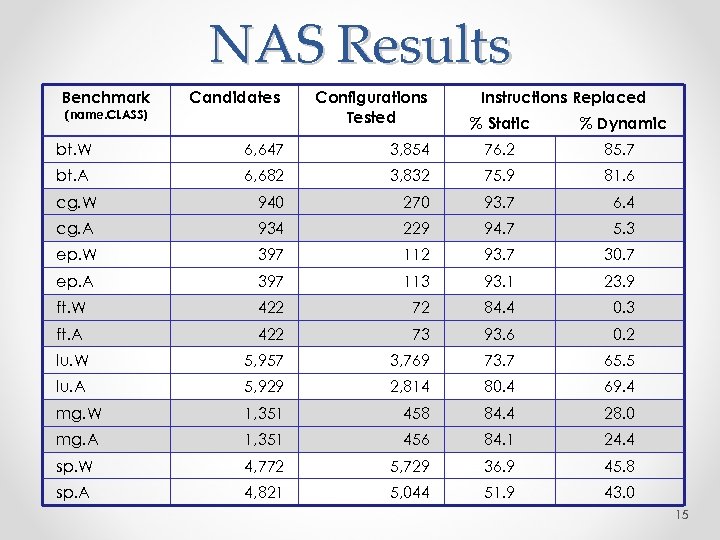NAS Results Benchmark (name. CLASS) Candidates Configurations Tested Instructions Replaced % Static % Dynamic bt. W 6, 647 3, 854 76. 2 85. 7 bt. A 6, 682 3, 832 75. 9 81. 6 cg. W 940 270 93. 7 6. 4 cg. A 934 229 94. 7 5. 3 ep. W 397 112 93. 7 30. 7 ep. A 397 113 93. 1 23. 9 ft. W 422 72 84. 4 0. 3 ft. A 422 73 93. 6 0. 2 lu. W 5, 957 3, 769 73. 7 65. 5 lu. A 5, 929 2, 814 80. 4 69. 4 mg. W 1, 351 458 84. 4 28. 0 mg. A 1, 351 456 84. 1 24. 4 sp. W 4, 772 5, 729 36. 9 45. 8 sp. A 4, 821 5, 044 51. 9 43. 0 15

AMGmk Results • Algebraic Multi. Grid microkernel • Multigrid method is highly adaptive • Good candidate for replacement • Automatic search • Complete conversion (100% replacement) • Manually-rewritten version • Speedup: 175 sec to 95 sec (1. 8 X) • Conventional x 86_64 hardware 16

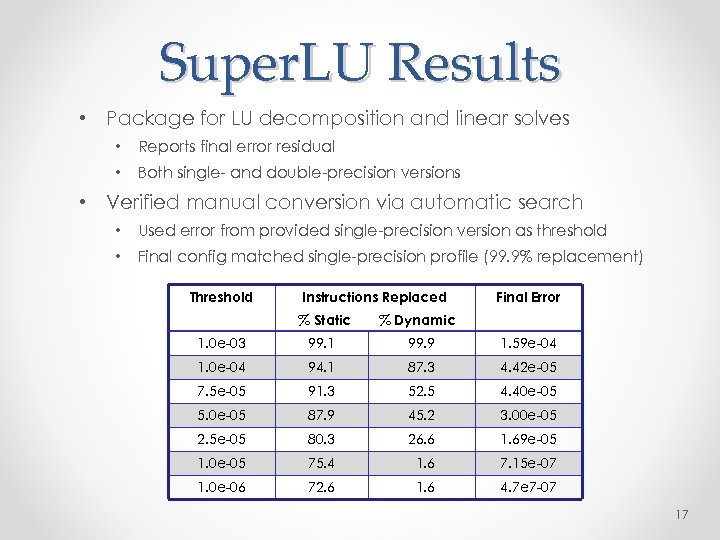Super. LU Results • Package for LU decomposition and linear solves • Reports final error residual • Both single- and double-precision versions • Verified manual conversion via automatic search • Used error from provided single-precision version as threshold • Final config matched single-precision profile (99. 9% replacement) Threshold Instructions Replaced % Static Final Error % Dynamic 1. 0 e-03 99. 1 99. 9 1. 59 e-04 1. 0 e-04 94. 1 87. 3 4. 42 e-05 7. 5 e-05 91. 3 52. 5 4. 40 e-05 5. 0 e-05 87. 9 45. 2 3. 00 e-05 2. 5 e-05 80. 3 26. 6 1. 69 e-05 1. 0 e-05 75. 4 1. 6 7. 15 e-07 1. 0 e-06 72. 6 1. 6 4. 7 e 7 -07 17

Retrospective • Twofold original motivation o Faster computation (raw FLOPs) o Decreased storage footprint and memory bandwidth o Domains vary in sensitivity to these parameters • Computation-centric analysis o Less insight for memory-constrained domains o Sometimes difficult to translate instruction-level recommendations to source code-level transformations • Data-centric analysis o Focus on data motion, which is closer to source code-level structures 18

Current Project • Memory-based replacement o Perform all computation in double precision o Save storage space by storing single-precision values in some cases • Implementation o Register-based computation remains double-precision o Replace movement instructions (movsd) o Memory to register: check and upcast o Register to memory: downcast if configured o Searching for replaceable writes instead of computes 19

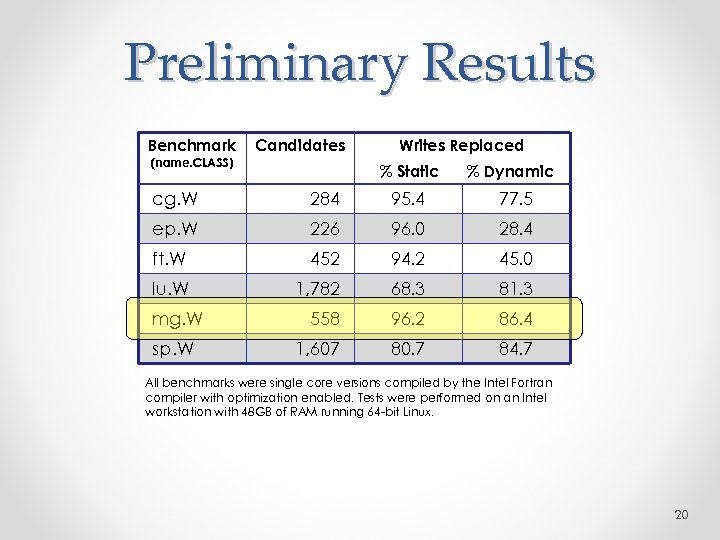Preliminary Results Benchmark (name. CLASS) Candidates Writes Replaced % Static % Dynamic cg. W 284 95. 4 77. 5 ep. W 226 96. 0 28. 4 ft. W 452 94. 2 45. 0 lu. W 1, 782 68. 3 81. 3 558 96. 2 86. 4 1, 607 80. 7 84. 7 mg. W sp. W All benchmarks were single core versions compiled by the Intel Fortran compiler with optimization enabled. Tests were performed on an Intel workstation with 48 GB of RAM running 64 -bit Linux. 20

21

22

23

24

25

26

27

Future Work • Case studies • Search convergence study 28

Conclusion Automated binary instrumentation techniques can be used to implement mixed-precision configurations for floating point code, and memory-based replacement provides actionable results. 29

Thank you! sf. net/p/crafthpc 30