01c27b14499c592b7f7b829eb2d12221.ppt
- Количество слайдов: 25

Flexible Spanners: A Proximity and Collision Detection Tool for Molecules and Other Deformable Objects Jie Gao, Leonidas Guibas, An Nguyen Computer Science Department Stanford University
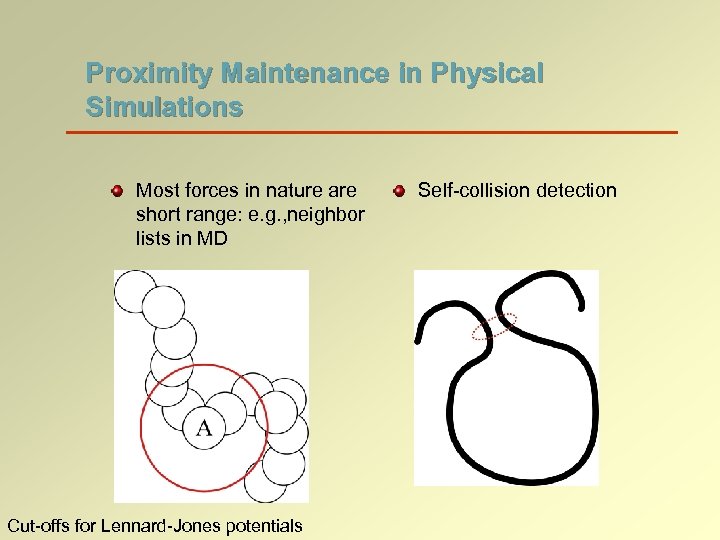
Proximity Maintenance in Physical Simulations Most forces in nature are short range: e. g. , neighbor lists in MD Cut-offs for Lennard-Jones potentials Self-collision detection

Models of Deformable Objects Deformable objects are modeled as connected collections of small elements of comparable size Focus mostly on “linear” objects (macromolecules, but also vines, ropes, chains) Each atom (element) moves a small distance after each simulation time step (discrete integration)

How much to know about object state? The integrator (MD) gives us the new positions of the atoms. How can we efficiently maintain self-proximity information, after small displacements of the atoms? To do so, we want to capture and maintain information that is useful for proximity detection yet is relatively stable and easy to update at the same time.

Traditional: Hashed Voxel Grids Partition space into a voxel grid and apportion the atoms of the molecule into cells of that grid Use a hash table, since many of the cells will be empty To find the neighbors of a given atom, search nearby cells Efficiency highly dependent on voxel grid size chosen For the right size grid, performs quite well for neighbor maintenance Usually requires re-hashing all the atoms when proximity information is desired Incremental updating can be good for end-game in folding, when atoms move only little Bad for unfolded phases, when there are few proximities but large motions cause many atoms to change cells

Traditional: Bounding Volume Hierarchies Bounding volume hierarchies (BVH), using spheres, bounding boxes, etc. , have been successfully used for collision checking of rigid objects Rigid bounding volume hierarchies are good for rigid objects, but Use a fair amount of space Collision checking requires a hierarchy traversal Hierarchy must be updated when deformation occurs
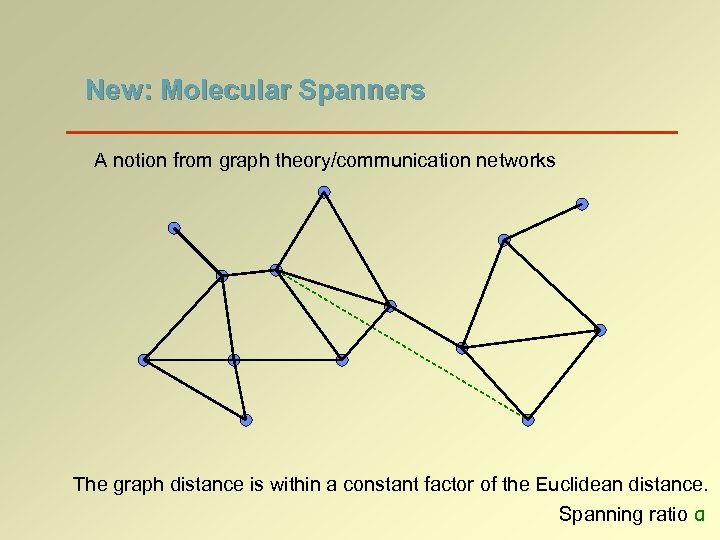
New: Molecular Spanners A notion from graph theory/communication networks The graph distance is within a constant factor of the Euclidean distance. Spanning ratio α
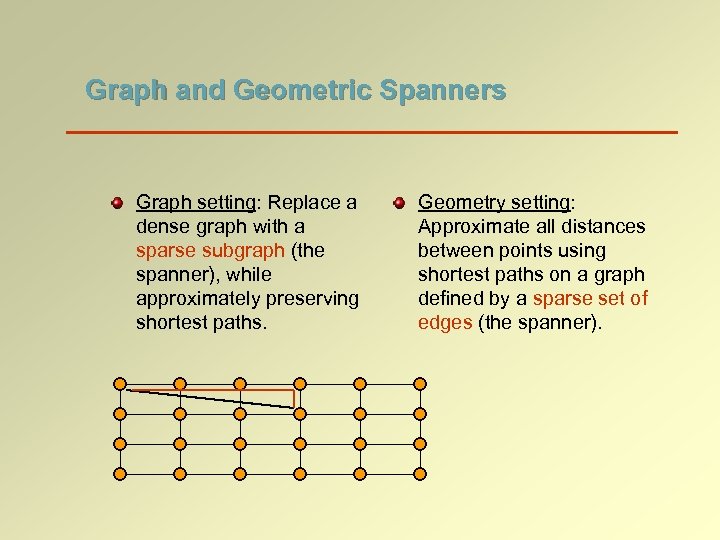
Graph and Geometric Spanners Graph setting: Replace a dense graph with a sparse subgraph (the spanner), while approximately preserving shortest paths. Geometry setting: Approximate all distances between points using shortest paths on a graph defined by a sparse set of edges (the spanner).

Spanners for Continuous Objects Add a sparse set of shortcuts, sufficient to guarantee the spanning property 3 HVT A protein example with α = 3

Spanners for Proximity Maintenance Lightweight, sparse, combinatorial structure Highly non-canonical Can be chosen so as to be very stable under smooth deformations (redundancy helps) To find all points at distance d from p, find all points within distance αd of p along the object and its shortcuts. Before two elements p and q on a deformable object can collide, there has to be a shortcut between them.
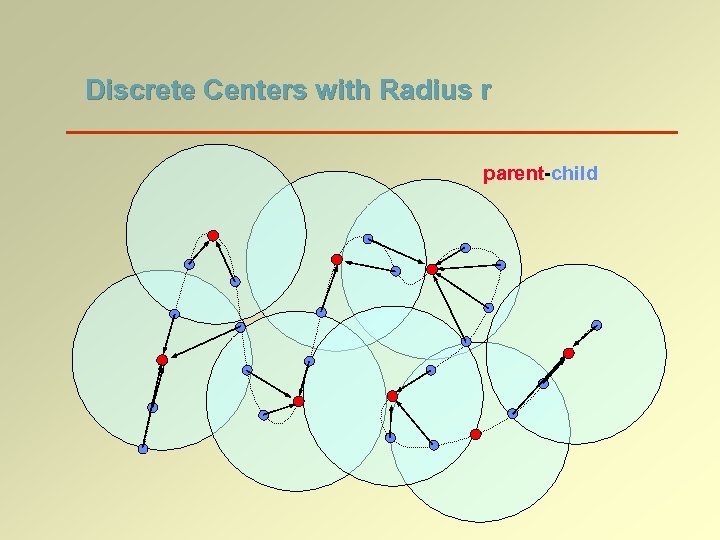
Discrete Centers with Radius r parent-child
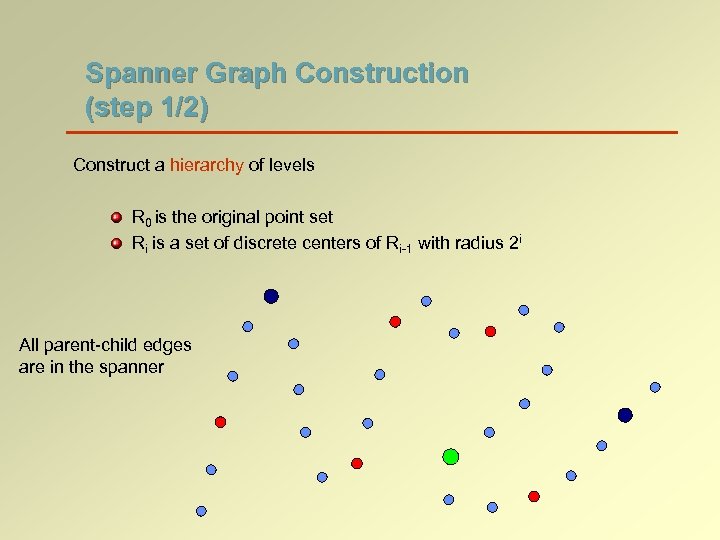
Spanner Graph Construction (step 1/2) Construct a hierarchy of levels R 0 is the original point set Ri is a set of discrete centers of Ri-1 with radius 2 i All parent-child edges are in the spanner
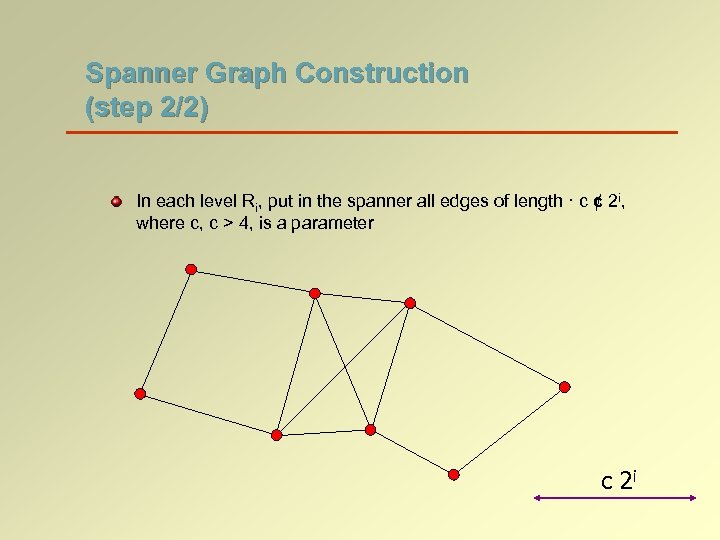
Spanner Graph Construction (step 2/2) In each level Ri, put in the spanner all edges of length · c ¢ 2 i, where c, c > 4, is a parameter c 2 i
![Spanner Theorem G is a (1+e)-spanner [expansion factor α = 1+e], where e = Spanner Theorem G is a (1+e)-spanner [expansion factor α = 1+e], where e =](https://present5.com/presentation/01c27b14499c592b7f7b829eb2d12221/image-14.jpg)
Spanner Theorem G is a (1+e)-spanner [expansion factor α = 1+e], where e = 16/(c-4). Level i · 2 i > c ¢ 2 i-1 Level i-1 · 2 i p q path(p, q) · |pq| + 8 2 i |pq| > (c - 4) 2 i-1 Level 0

More Spanner Observations In level Ri Nodes are at least 2 i apart Edges have length at most c ¢ 2 i Number of nodes is O(n/2 i) Each node is incident to at most O(1) edges Number of edges is O(n/2 i) Total length of all edges is O(n)

Spanner Quality Linear size: O(n) edges Total length of all edges: O(n log n) Maximum degree of a node: O(log n)

Maintenance under Deformation The correctness of the spanner can be certified by O(n) KDS -style certificates. These are all simple distance inequalities on the lengths of spanner edges. After each integration step we must verify and update the spanner – may need to deal with multiple certificate failures: Verify and update the hierarchy Verify and update spanner edges We can exploit conservative bounds on failure times of certificates derived from prior node velocity bounds to avoid checking all certificates at each step.
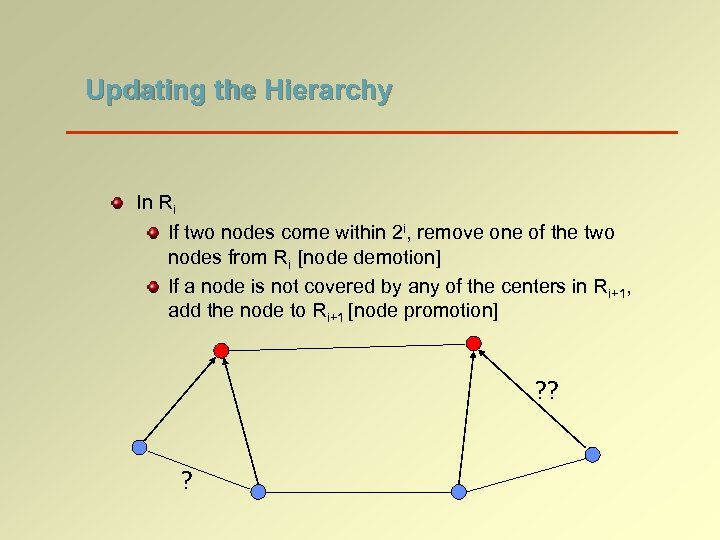
Updating the Hierarchy In Ri If two nodes come within 2 i, remove one of the two nodes from Ri [node demotion] If a node is not covered by any of the centers in Ri+1, add the node to Ri+1 [node promotion] ? ? ?
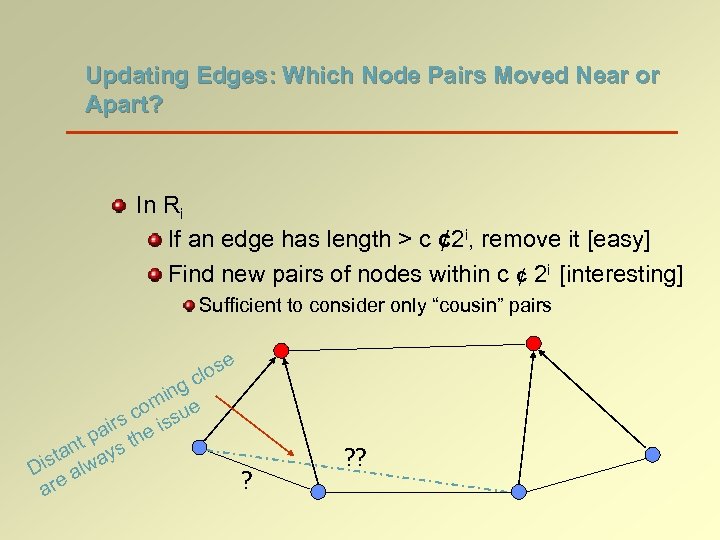
Updating Edges: Which Node Pairs Moved Near or Apart? In Ri If an edge has length > c ¢ 2 i, remove it [easy] Find new pairs of nodes within c ¢ 2 i [interesting] Sufficient to consider only “cousin” pairs e s clo ing m co sue s air he is p nt ys t ista lwa D a are ? ? ?
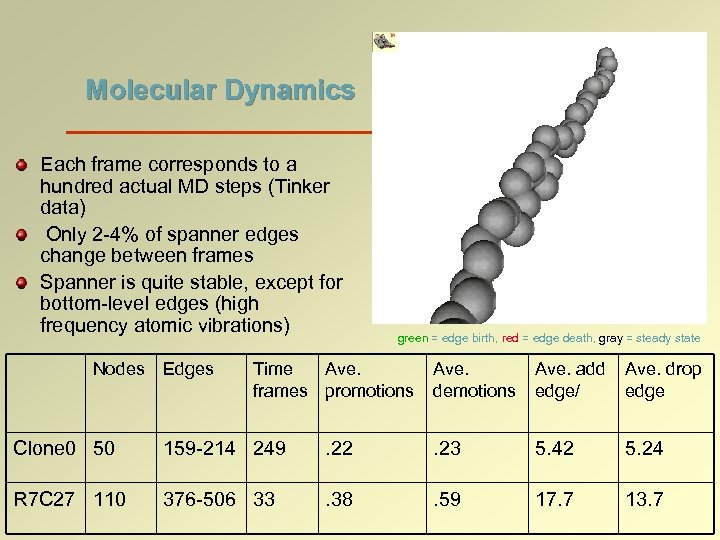
Molecular Dynamics Each frame corresponds to a hundred actual MD steps (Tinker data) Only 2 -4% of spanner edges change between frames Spanner is quite stable, except for bottom-level edges (high frequency atomic vibrations) Nodes Edges green = edge birth, red = edge death, gray = steady state Time Ave. frames promotions Ave. demotions Ave. add edge/ Ave. drop edge Clone 0 50 159 -214 249 . 22 . 23 5. 42 5. 24 R 7 C 27 110 376 -506 33 . 38 . 59 17. 7 13. 7
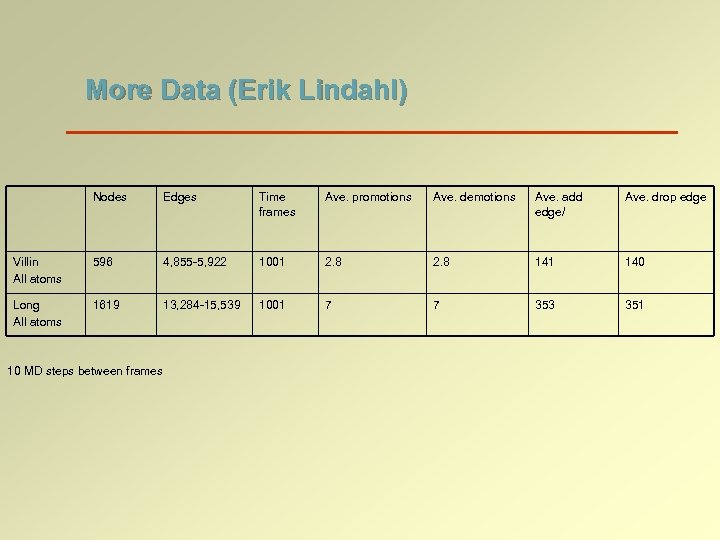
More Data (Erik Lindahl) Nodes Edges Time frames Ave. promotions Ave. demotions Ave. add edge/ Ave. drop edge Villin All atoms 596 4, 855 -5, 922 1001 2. 8 141 140 Long All atoms 1619 13, 284 -15, 539 1001 7 7 353 351 10 MD steps between frames

Additional Spanner Properties, I Can be used to compute neighbor lists within any distance constraint, in an output-sensitive manner Number of pairs of atoms examined is proportional to the number of pairs reported
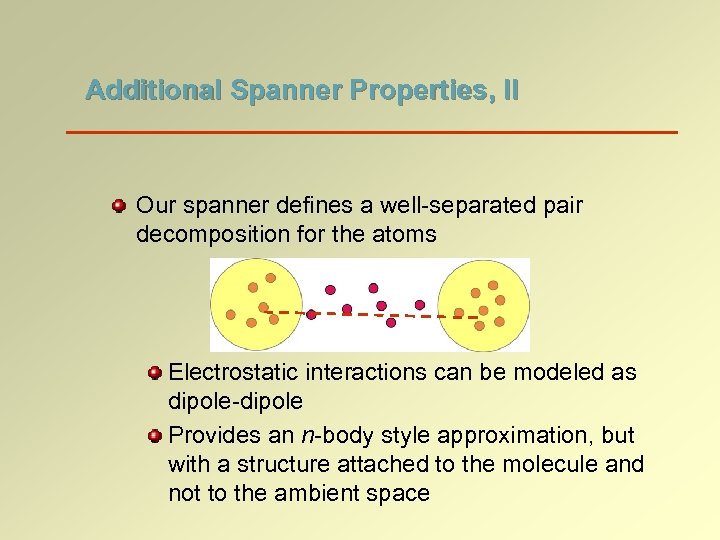
Additional Spanner Properties, II Our spanner defines a well-separated pair decomposition for the atoms Electrostatic interactions can be modeled as dipole-dipole Provides an n-body style approximation, but with a structure attached to the molecule and not to the ambient space
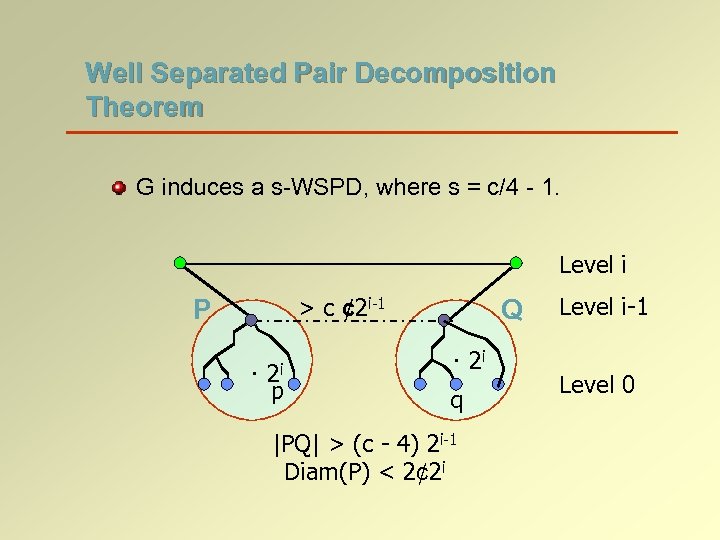
Well Separated Pair Decomposition Theorem G induces a s-WSPD, where s = c/4 - 1. Level i > c ¢ 2 i-1 P · 2 i p Q · 2 i q |PQ| > (c - 4) 2 i-1 Diam(P) < 2¢ 2 i Level i-1 Level 0

Final Remarks Unlike bounding volume hierarchies, the spanner is a lightweight, combinatorial structure Unlike voxel grids, the spanner is essentially unchanged for mostly rigid molecular motions We are also using it for macro-level simulations (rope, chain, filament) A Cosserat rope
01c27b14499c592b7f7b829eb2d12221.ppt