4797604e9f6b4ec378c183a717cef97d.ppt
- Количество слайдов: 12

Flexible Graph Models for Complex Networks Yorgos Amanatidis 1 Complex Networks: Internet and its applications: WWW, content sharing, social online Other: further social, biological Flexible Graph Models: Few parameters whose fine tuning result in vastly distinct features of (possibly annotated) network structure and function. Fundamental to explain, predict and control network function. We also focus on efficiency of model realizability, since the scaling rate of the related applications is quite dramatic. Poster Outline: Pages 2, 3: Brief Summary of Standard Complex Network Models Page 4: Two Low Entropy Cases: Disassortativity and Sparse Cuts Pages 5, 6, 7, 8: The Joint Degree Matrix Realizability Problem (addressing the case of disassortative networks) Pages 9, 10, 11: Random Kernel (similarity) Graphs (towards generalizing standard models to include distinct special cases such as sparse cuts and disassortativity) Page 12: Network Evolution and Efficient Implementation Joint with Bradley Green 2, Milena Mihail 3 (advisor) 1. School of Mathematics, Georgia Tech, supported by ARC and ACO. 2. School of Mathematics, Georgia Tech, supported by NSF VIGRE. 1 3. School of Computer Science, Georgia Tech, supported by NSF CCF 05 & 08.

Structure & Function Early Observations Structure: Heavy Tailed Statistics Nearly constant average degree (as the network scaled) but no concentration of degrees around their mean. Suggest paradigm shift from Erdős-Rényi models. AS Level Internet (each node is an ISP) Gene-Protein Interaction network for the Yeast Function: Small World Phenomenon Local clustering and small diameter, especially navigability. Suggest function as an integral part of model definition and evaluation. Navigability stresses importance of accurate parametrization. In a clustered graph of size n, O(n) random links decrease the diameter to O(logn) When the O(n) links are added with then paths of length O(polylogn) can be found with local search, 2 iff r is the dimension of the lattice.

Complex Network Models 1 st Generation Macroscopic (see R. Durrett’s book 08) Random graphs capturing heavy tailed statistics. Further effort to verify the models by establishing efficient network function (diameter, conductance, navigability) Advantages: conceptually simple, General, efficient to implement. Disadvantage: missing semantics Successful: when all network elements are roughly similar, Thus the missing semantics are not particularly important. Example: AS Level Internet (all ISP’s are more or less the same). Microscopic (see M. Jackson’s book 08) Explanatory: evolutionary/optimization/incentive-driven processes. Further effort to verify the models by establishing agreement with observed structural properties. Advantage: fully annotated and explanatory. Disadvantages: lack of generality, particularly inefficient to simulate Successful: in cases where network elements have strongly distinct semantics. Example: Internet router connectivity within an ISP. There is vast variance in the capacities of different routers 3
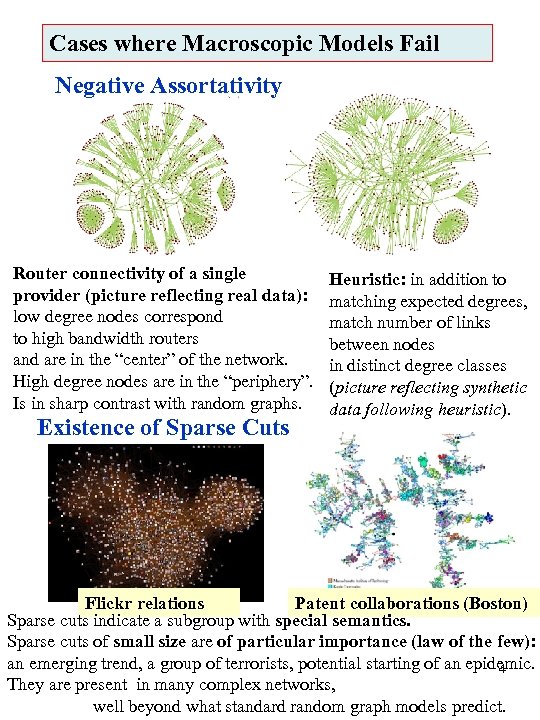
Cases where Macroscopic Models Fail Negative Assortativity Router connectivity of a single provider (picture reflecting real data): low degree nodes correspond to high bandwidth routers and are in the “center” of the network. High degree nodes are in the “periphery”. Is in sharp contrast with random graphs. Existence of Sparse Cuts Heuristic: in addition to matching expected degrees, match number of links between nodes in distinct degree classes (picture reflecting synthetic data following heuristic). Flickr relations Patent collaborations (Boston) Sparse cuts indicate a subgroup with special semantics. Sparse cuts of small size are of particular importance (law of the few): an emerging trend, a group of terrorists, potential starting of an epidemic. 4 They are present in many complex networks, well beyond what standard random graph models predict.

Graphic Realizations of Joint Degree Matrices addressing negative assortativity The Joint-Degree Matrix Realization Problem: The J-D Matrix Connected Realization Problem: 5
![Theorem 1 [A, Green, Mihail ’ 08]: (generalization of Erdős-Gallai, Havel-Hakimi) Theorem 2 [A, Theorem 1 [A, Green, Mihail ’ 08]: (generalization of Erdős-Gallai, Havel-Hakimi) Theorem 2 [A,](https://present5.com/presentation/4797604e9f6b4ec378c183a717cef97d/image-6.jpg)
Theorem 1 [A, Green, Mihail ’ 08]: (generalization of Erdős-Gallai, Havel-Hakimi) Theorem 2 [A, Green, Mihail ’ 08]: 6
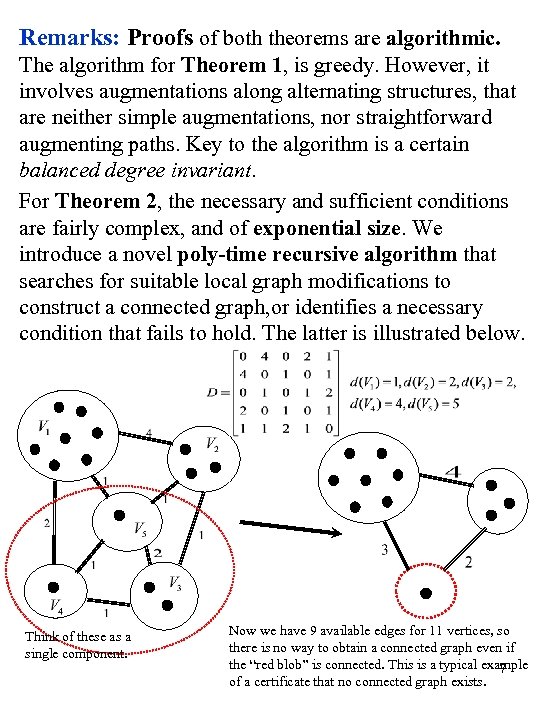
Remarks: Proofs of both theorems are algorithmic. The algorithm for Theorem 1, is greedy. However, it involves augmentations along alternating structures, that are neither simple augmentations, nor straightforward augmenting paths. Key to the algorithm is a certain balanced degree invariant. For Theorem 2, the necessary and sufficient conditions are fairly complex, and of exponential size. We introduce a novel poly-time recursive algorithm that searches for suitable local graph modifications to construct a connected graph, or identifies a necessary condition that fails to hold. The latter is illustrated below. Think of these as a single component. Now we have 9 available edges for 11 vertices, so there is no way to obtain a connected graph even if the “red blob” is connected. This is a typical example 7 of a certificate that no connected graph exists.

Open Problems 8

Random Kernel Function Graphs Motivation: Nodes have semantics expressed by values on d distinct attributes, and are generated from a general distribution. Connections between nodes have semantics expressed by a kernel function. Model (slightly simplified for this poster): Model : 9

Known Results for Random Kernel Graphs Bollobás, Janson, Riordan 07: Semiclosed characterization of connectivity and phase transition in terms of (under mild assumptions). Subsumes most known sparse random graph models by suitable definitions of. Main point: vast classes of sparse random graphs reduce locally (and can be analyzed) like Erdős-Rényi. Young, Mihail 08: Characterization (with concentration) of degree distribution, diameter, clustering, in terms of. Includes heavy tailed models and small world phenomenon by suitable definition of (without assumptions). Semiclosed characterization of conductance, in terms of (conjectured if a. e. ) Main point: there is a random graph model with clear semantics, conceptually simple and efficient to implement, that captures many critical structural and functional aspects of complex networks, and generates quite distinct classes graphs. Main challenge: Model with whose characterization reduces to 10

Probability Distributions & Kernel Functions towards modeling Sparse Cuts In theory, for wide ranges of network characteristics (using Young & Mihail 08), and experimentally A & Mihail 08). Probability Distributions & Kernel Functions towards modeling Negative Assortativity Experimentally A & Mihail 08. 11

Evolution The general allows each instance to evolve naturally from previous instances. Efficient Implementation In general, realizing an instance of requires experiments. For where expected degrees can be computed efficiently (including inner product graphs), this can be reduced to by “approximating” the distribution as in the configuration model. It is interesting to prove guarantees for such approximations. In principle, the introduced dependencies only force degree concentration, and we expect good behavior. 12
4797604e9f6b4ec378c183a717cef97d.ppt