Физика Земли Реология мантии и модели конвекции ГЕОФИЗИКА

Физика Земли Реология мантии и модели конвекции ГЕОФИЗИКА Лекция 14

Реологические свойства • Деформация горных пород при длительном нагружении не является полностью упругой и обратимой: ползучесть, явления упругого последействия, пластичность. Описание неупругого поведения тел основано на определяющих реологических уравнениях, связывающих касательные напряжения с соответствующими деформациями и их скоростями. На гидростатическое давление тела реагируют по закону Гука. • На основе данных о поведении материалов при разных способах нагружения (по интенсивности, длительности) определяются связи между касательными напряжениями и деформациями и их скоростями. Им соответствуют идеальные реологические тела. • 2

Реологические тела • Тело Гука Н – упругость; • Тело Ньютона N – вязкость; • Тело Сен-Венана St. V – пластичность. • Эти три тела образуют тела более сложные – путем их параллельного | или последовательного — соединения: • Тело Максвелла М = N — H; • Тело Кельвина K = H | N; • Тело Прандтля P = St. V— H; • Тело Бюргерса Bu = M — K; • Тело Джеффриса J = N | M; • Тело Бингама 3 B = H — (St. V | N).

Механический смысл сложных реологических тел Тело Максвелла М = N — H: упруго-вязкая жидкость. • Тело Кельвина K =H | N: твердое тело с упругим последействием. • Тело Прандтля P = St. V— H: упруго-пластичное твердое тело. • Тело Бюргерса Bu = M — K: вязко-упругое твердое тело. • Тело Джеффриса J = N | M: релаксация упругих напряжений. • Тело Бингама B = H — (St. V | N): вязко-пластичное тело. Если простое определяющее соотношение не позволяет с необходимой точностью описать процесс, вводят нелинейную зависимость между напряжениями, деформациями и их скоростями. 4

Реология мантии • Механизмы ползучести и вязкого течения материала определяются реологическими свойствами, зависящими от температуры и давления. • В мантии Земли работают два механизма ползучести. • При уровне касательных напряжений ≤ 107 Па, характерном для конвекции, деформация идет путем диффузионного массопереноса. • Диффузионная ползучесть – линейная зависимость между напряжениями и скоростью деформации; коэффициент пропорциональности между ними – вязкость η; среда – ньютоновская жидкость. • При уровне напряжений ≥ 108 Па деформация идет путем движения дислокаций. Зависимость между скоростью деформации и напряжениями нелинейная – неньютоновская жидкость. • В мантии могут действовать оба механизма; при данных Р−Т условиях порода деформируется по механизму, который дает наивысшую скорость деформирования. 5

Реология оливина • Главным компонентом состава мантии является оливин. Можно считать, что реология верхней мантии определяется его поведением. • При стационарном деформировании оливина скорость деформации от температуры и давления зависит экспоненциально, а от размера зерен и касательных напряжений имеет степенную зависимость. • В разных механизмах деформирования роль этих параметров различна. При дислокационном крипе скорость деформирования не зависит от размера зерен. Диффузионный механизм превалирует над дислокационным крипом при малом размере зерен, низкой температуре и высоком давлении. • Кроме того, значение вязкости материала сильно зависит от степени насыщенности его флюидами. 6

Вязкость оливина • Экспериментальные данные о зависимости скорости деформации от напряжений в оливине: глубина 100 км; размер зерен d = 14 мкм; сухие условия (dry). • Асимптоты ползучести: diff – диффузионная, dis – дислокационная. 7

Вязкость по данным о послеледниковом поднятии • Метод изучения распределения вязкости по глубине – изучение режима поднятий земной поверхности после исчезновения ледников (Канада, Фенноскандия). • Созданы численные модели, с хорошей точностью описывающие пространственно-временные характеристики процесса изостатического постгляциального поднятия. Одним из результатов является доказательство существования астеносферы под стабильными докембрийскими щитами, что не было известно из других геофизических данных. • Совпадение расчетных и наблюдаемых скоростей поднятия Балтийского и Канадского щитов получено для модели: толщина литосферы ≥ 200 км, толщина астеносферы 75 км, вязкость астеносферы под Балтийским щитом 1, 5∙ 1019 Па∙с, под Канадским щитом 5∙ 1018 Па∙с , вязкость верхней мантии под обоими щитами 0, 7∙ 1021 Па∙с. 8

Вязкость мантии • Под молодыми платформами и складчатыми поясами толщина литосферы 100− 150 км. Астеносфера имеет вязкость ~ 1018 Па∙c. • Итак, имеет переменную толщины и лежит на верхняя мантия с вязкостью ~∙ 1021 Па∙c. • Непосредственно под жесткой недеформируемой литосферой древних платформ лежит астеносфера толщиной 75− 80 км с вязкостью ~1019 Па∙c; в активных областях континентов и в океанах толщина астеносферы – до 300 км, а вязкость уменьшается – до 1018 Па∙c под континентами и океаническими котловинами и до 1017 Па∙c под океаническими хребтами. • Вязкость верхней мантии вблизи ФПЗ близка к 1022 Па∙c. При переходе в нижнюю мантию она возрастает в 50− 200 раз (по оценкам разных исследователей). 9

Вязкость литосферы 10

Вязкость в переходной зоне мантии • Фазовая переходная зона мантии: схема структуры, плотности и вязкости. • Обозначения: • α – оливин верхней мантии; • α + β, β, β + γ, γ, γ + pv – переходная зона с прослоями смешанных фаз; • pv – плюм в нижней мантии; Такая структура мантии позволяет • pv + mw – состав нижней мантии: перовскит с разводить в ФПЗ встречные магнезио-вюститом потоки верхне- и нижнемантийной конвекции, сохраняя положение 11 теплового канала.

Неоднородность астеносферы и ФПЗ 12

Раздел 670 км – барьер для конвекции 13

Двухярусная термохимическая конвекция • 1. Основная генерация положительной плавучести (создание относительно легкого вещества) происходит на границе ядромантия в результате развивающейся здесь гравитационной дифференциации мантийного вещества. • 2. Основная генерация отрицательной плавучести (создание относительно тяжелого вещества) происходит в верхней мантии в зонах субдукции океанской коры за счет ее эклогитизации. • 3. Конвекции в принципе может иметь две моды: • 1) двухярусную моду, когда ячейки в нижней и верхней мантии развиваются без обмена веществом через разделяющую их фазовую границу; • 2) одноярусную моду, которая характеризуется прорывом через фазовую границу вещества нижней мантии в верхнюю и наоборот. 14

Следствия термохимической конвекции • Модель термохимической конвекции описывает главные закономерности геодинамического процесса: а) поднимающиеся с границы ядро-мантия суперплюмы, которые образуют в верхней мантии региональные плюмы на фазовой границе 670 км; • б) погружающиеся в зонах субдукции вместе с плитами тяжелые эклогитовые массы задерживаются на границе 670 км, иногда накапливаются в виде крупных линз; при достижении критического объема эти тяжелые линзы “проваливаются” в нижнюю мантию. • Эта модель объясняет цикл Вильсона с периодическим образованием и распадом суперконтинентов-Пангей в эволюции Земли. • Такие циклы вероятны в тихоокеанском полушарии, где периодически должны были возникать конвергентные зоны и островодужные комплексы, которые при смене циркуляции конвективных ячеек должны разноситься к континентальным 15 окраинам.

Модели конвекции 16

Физическая модель конвекции

Геометрия математической модели конвективной структуры 18

Тепловые пограничные слои конвективных ячеек 19

Конвекция в мантии (Добрецов и др. , 2001) 20

Стадии развития плюма Математическая модель 21

Физическая модель развития неустойчивости Рэлея - Тейлора 22

Характерный вид плюмов 23

Главное геомагнитное поле

В геомагнетизме и магниторазведке основным элементом магнитного поля является вектор T. До введения СИ его считали напряженностью поля H, измеряли в эрстедах (Э), в гаммах (γ), 1 γ = 10− 5 Э. Сейчас вектор T рассматривают как магнитную индукцию B, что физически точнее: магнитное поле измеряется не в вакууме. Единицы T в CИ – тесла (Тл) и нанотесла (н. Тл), 1 н. Тл = 10− 9 Тл. Материалы старых магнитных съемок можно использовать без исправления, так как 1 γ = 1 н. Тл. Это допустимо ввиду одинаковых значений (в СГС) B и H и размерности Э и Гс: 1 γ = 10− 5 Э = 10− 5 Гс = 10− 9 Тл = 1 н. Тл. Магнитная индукция B – силовая функция геомагнитного поля (T ≡ B). Для выполнения условия B = grad U потенциал U определим через произведение магнитного момента диполя М и постоянной μ 0 / 4π: 26

Геомагнитное поле (ГМП) в первом приближении является дипольным как поле однородно намагниченного шара или поле кольцевого тока, текущего в экваториальной плоскости. На поверхности сферы радиуса R вертикальная Z и горизонтальная H производные геомагнитного потенциала U: φ − широта. Если ось диполя не совпадает с осью вращения, вместо широты φ используют магнитную широту φм. Модуль T вектора магнитной индукции T дипольного магнитного поля равен Поле Z изменяется от 0 на экваторе до 2 M / R 3 на полюсах, поле H − от 0 на полюсах до M / R 3 на экваторе; Т − от M / R 3 на экваторе до 2 M / R 3 на полюсах. Наклонение I вектора магнитной индукции T к горизонту Поэтому tg I = 2 tg φ. 27

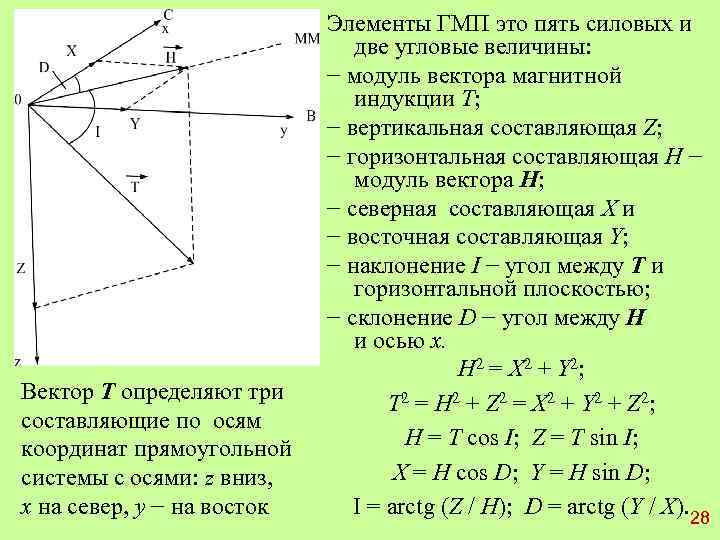Вектор T определяют три составляющие по осям координат прямоугольной системы с осями: z вниз, x на север, y − на восток Элементы ГМП это пять силовых и две угловые величины: − модуль вектора магнитной индукции T; − вертикальная составляющая Z; − горизонтальная составляющая H − модуль вектора Н; − северная составляющая X и − восточная составляющая Y; − наклонение I − угол между Т и горизонтальной плоскостью; − склонение D − угол между Н и осью x. H 2 = X 2 + Y 2; T 2 = H 2 + Z 2 = X 2 + Y 2 + Z 2; H = T cos I; Z = T sin I; X = H cos D; Y = H sin D; I = arctg (Z / H); D = arctg (Y / X). 28

Структура геомагнитного поля Значения T на поверхности – от 23 000 до 68 000 н. Тл; значение T на экваторе ~32 000 н. Тл, на полюсах ~66 000 н. Тл. Поле соответствует диполю в центре Земли с магнитным моментом M = 8, 05∙ 1022 A∙м 2 (8, 05∙ 1015 Тл∙м 3). Значения |Z| вблизи полюсов составляют ~64 000 н. Тл, Н в области экватора ~30000 н. Тл. Ось такого диполя пересекает поверхность Земли в геомагнитных полюсах. Магнитные полюса это точки на поверхности Земли, где наклонение I = 90°, а горизонтальная составляющая Н = 0. Из-за неоднородности аномального поля магнитные полюса это области, где условия выполняются приближенно. Наклон α оси диполя к оси вращения Земли определяется по широте северного геомагнитного полюса: α = 90° – φ. Наклон в последние эпохи был: 1960 − 11, 5 °, 1980 − 11, 2°, 2000 г. − 10, 5 °. 29

Координаты геомагнитных и магнитных полюсов (Международное геомагнитное поле IGRF 10 -й генерации) Геомагнитные Год Северный Южный φ φ Магнитные λ Северный λ φ λ Южный φ λ 1960 78, 5 − 69, 5 − 78, 5 111, 5 75, 3 − 101, 0 − 66, 7 140, 2 1980 78, 8 − 70, 7 − 78, 8 111, 2 76, 9 − 101, 7 − 65, 4 139, 3 2000 79, 5 − 71, 6 − 79, 5 110, 5 81, 0 − 109, 6 − 64, 7 138, 3 Широта φ и долгота λ геомагнитных и магнитных полюсов на эпохи 1960, 1980 и 2000 гг. –С 1995 г. миграция северного магнитного полюса резко ускорилась. За последние 10 лет он сместился на 500 км к географическому полюсу. Такое же расстояние он прошел за 50 лет с 1945 по 1995 г. Смещение геомагнитного полюса намного меньше - за 100 лет на 150 км. Южный магнитный полюс за 100 лет сместился к северо-западу на 700 км, а геомагнитный – только на 100 км. 30

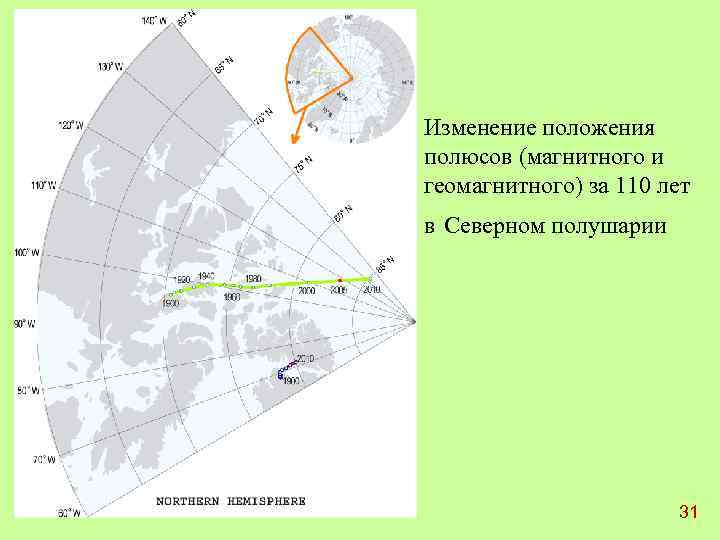Изменение положения полюсов (магнитного и геомагнитного) за 110 лет в Северном полушарии 31

Изменение положения полюсов (магнитного и геомагнитного) за 110 лет в Южном полушарии 32

Спектр геомагнитного поля: квадрат амплитуды гармоники в функции ее номера. Основная кривая – поле на земной поверхности – показывает, что главное поле описывается гармониками 1 – 13. Верхняя кривая – поле на поверхности ядра – главная часть до 13 гармоники уменьшается, амплитуда высоких гармоник растет. Это поля токовых систем на поверхности жидкого внешнего ядра. 33

Аномальное магнитное поле проявляется в коэффициентах Гаусса случайным образом из-за малых размеров аномалий в плане (десятки километров и менее). В главном геомагнитном поле можно выделить: а) дипольное поле (ДП), описываемое первой и второй гармониками; его величина в среднем по интенсивности на земной поверхности составляет около 90 % полного ГМП; б) поле мировых магнитных аномалий (ММА), определяемое гармониками от 1 до 8 порядка. Выделены 4 такие аномалии: положительные Сибирская, Канадская и Антарктическая и отрицательная Бразильская. ММА составляют основную часть недипольного поля, которое отличается от дипольного морфологией и закономерностями изменения во времени. 34

Z H 35

Карта Т (F) 2005 36

Вариации геомагнитного поля Геомагнитное поле очень нестабильно; вариации ГМП: 1. Уменьшение магнитного момента M и амплитуды первой гармоники g 10; d. M/Mdt = – 5· 10– 4 год– 1 за 150 лет, а за 1980– 2000 гг. она равна – 7· 10– 4 год– 1. Если бы скорость была постоянной, поле могло уменьшиться до нуля за 2000 лет, но она меняется. 2. Инверсии геомагнитного поля; в последние 5 млн лет изучены 22 инверсии. Выделены две эпохи прямой (современной) полярности: Брюнес (от 0, 87 млн лет до настоящего времени), Матуяма (2, 40– 0, 87 млн лет), и две эпохи обратной полярности – Гаусс (3, 32– 2, 40 млн лет) и Гилберт (5, 20– 3, 32 млн лет). Каждая из них включает эпизоды противоположной полярности длительностью 0, 02– 0, 2 млн лет. За 230 млн лет, в мезозое и кайнозое, одна инверсия приходилась на (2– 5)· 105 лет. Длительность изменения полярности составляет 103– 104 лет. 37

Каждая из эпох включает эпизоды противоположной полярности длительностью 0, 02– 0, 2 млн лет. За 230 млн лет, в мезозое и кайнозое, одна инверсия приходилась на (2– 5)· 105 лет. Длительность изменения полярности составляет 103– 104 лет 38

3. Изменения параметров эксцентричного диполя за 50 лет (1955– 2005 гг. ): а) удаление центра диполя от центра Земли на 120 км; б) смещение центра ЭД на север от экватора на 4, 6º; 4. Уменьшение дипольного поля сопровождается увеличением интенсивности 2 -й гармоники. 5. Вариации недипольной части поля: возникновение фокусов векового хода, их западный дрейф со скоростями 0, 18– 0, 23 град/год и распад (через 20– 60 лет). 6. Квазипериодические вариации интенсивности элементов ГМП: периоды: 6, 11, 22, 58, 450, 600, 1800, 8000 лет (6, 11 и 22 связаны с внешним полем). Вариация с периодом 8000 лет является основной для формирования дипольного магнитного момента. Около 2 тыс. лет назад он был максимален – в 1, 5 раза больше, а 6 тыс. лет назад – вдвое меньше современного. 39

40

Схема гидромагнитного динамо 41

Earthquake Location Magnitude 9. 0 NEAR EAST COAST OF HONSHU, JAPAN Friday, March 11, 2011 at 05: 46: 23 UTC