Физика твердого тела СПб ГПУ ФТФ 2012 -2013

Зарегистрируйтесь, чтобы просмотреть полный документ!

Физика твердого тела СПб. ГПУ, ФТФ, 2012 -2013 учебный год Алексей Акимович Торопов Д. ф. -м. наук, ведущий научный сотрудник: лаб. "Физики квантоворазмерных гетероструктур", Физико-технический институт им. А. Ф. Иоффе Профессор: кафедра "Физика твердого тела", Физико-технический факультет, СПб. ГПУ Телефоны: 292 -7124 (ФТИ) 271 -0239 (дом) 904 -7196 (моб) Факс: 297 -1017 Email: toropov@beam. ioffe. ru

Современные научные интересы: - Оптическая спектроскопия полупроводниковых наноструктур: квантовых ям, сверхрешеток, квантовых точек; - Разбавленные магнитные полупроводники. Спин-зависимые явления; - Экситон-плазмонные свойства композитных наноструктур металл - полупроводник.

Лекция 1 (05. 09. 2011) 1. Чем занимается наука "Физика твердого тела" ? - Что мы понимаем под твердыми телами ? - Исторический аспект: Нобелевские премии 2. Организационные вопросы 3. Структура кристаллов Литература: 1. А. И. Ансельм, “Введение в теорию полупроводников” 2. Ландау и Лифшиц, том III "Квантовая механика", Глава XII 3. Ландау и Лифшиц, том V “Статистическая физика, часть 1", Глава XIII 4. Г. Л. Бир и Г. Е. Пикус, “Симметрия и деформационные эффекты в полупроводниках”

Твердые тела - что это такое? Состояния вещества: твердое, жидкое, газообразное, плазма. . .

Физика твердого тела в современном понимании началась 8 июня 1912 г. Баварская Академия наук. Мюнхен. Доклад “Интерференция рентгеновских лучей”. 1 -я часть – Макс Теодор Феликс фон Лауэ изложил элементарную теорию дифракции рентгеновских лучей на периодическом атомном ряде. 2 -я часть – Сообщение Вальтера Фридриха и Паула Книппинга о первых экспериментальных наблюдениях дифракции рентгеновских лучей в кристаллах. Неопровержимые доказательства, что кристаллы состоят из периодических рядов атомов.

Нобелевские премии по физике в области ФТТ 1914 г. Макс Теодор Феликс фон Лауэ: За открытие дифракции рентгеновских лучей в кристаллах 1915 г. Уильям Генри Брэгг и Уильям Лоренс Брэгг: За заслуги в исследовании структуры кристаллов с помощью рентгеновских лучей 1920 г. Шарль Гильом: В знак признания его заслуг перед точными измерениями в физике – открытия аномалий в никелевых стальных сплавах (сплав элинвар) 1956 г. Джон Бардин, Уолтер Браттейн, Уильям Шокли: За исследования полупроводников и открытие транзисторного эффекта 1972 г. Джон Бардин, Леон Купер, Роберт Шриффер: За совместное создание теории сверхпроводимости, обычно называемой БКШ-теорией

1973 г. Лео Есаки, Брайн Джозевсон, Айвар Джайевер: За экспериментальные открытия явлений туннелирования в полупроводниках и сверхпроводниках 1977 г. Филип Андерсон, Невилл Мотт, Джон Ван Флек: За фундаментальные теоретические исследования электронной структуры магнитных и неупорядоченных систем 1985 г. Клаус фон Клитцинг: За открытие квантового эффекта Холла 1987 г. Георг Беднорц и Карл Мюллер: Открытие высокотемпературной сверхпроводимости в керамических материалах 1991 г. Пьер Жиль де Жен: За обнаружение того, что «методы, развитые для изучения явлений упорядоченности в простых системах, могут быть обобщены на более сложные формы материи, в частности на жидкие кристаллы и полимеры» . 1998 г. Роберт Лаффлин, Хорст Штёрмер, Даниэль Цуи: За открытие новой формы квантовой электронной жидкости - частиц с дробным электрическим зарядом (дробный квантовый эффект Холла)

2000 г. Жорес Иванович Алферов и Герберт Крёмер, Джек Килби: За "разработки в полупроводниковой технике" и "исследования в области интегральных схем" 2007 г. Альбер Фер и Петер Грюнберг: За открытие в 1988 году эффекта гигантского магнетосопротивления 2009 г. Чарльз Као, Джордж Смит и Уиллард Бойл: За "выдающиеся достижения в области передачи света по оптоволоконному кабелю" и "изобретение прибора с зарядовой связью (ПЗС)". 2010 г. Константин Новоселов и Андрей Гейм: За “новаторские эксперименты по исследованию двумерного материала графена". 2011 г. Даниэль Шехтман: За “открытие квазикристаллов". (премия по химии)

Развитие электродинамики, квантовой механики и других составляющих аппарата физики твердого тела: Вильгельм Рентген (1901 г), Хендрик Лоренц и Питер Зееман (1902), Макс Планк (1918), Нильс Бор (1922), Луи де Бройль (1929), Вернер Гейзенберг (1932), Поль Дирак и Эрвин Шредингер (1933), Вольфганг Паули (1945), Феликс Блох (1952), Макс Борн (1954), . .

Организация процесса 1. Использование компьютерной техники. 2. Занятия: лекции и иногда семинары по мере надобности. 3. Учет и контроль. Система "плюс-минусов" - домашние задачи с разбором наиболее важных на семинарах (+) - контрольные вопросы в конце каждого занятия (+) - проведение студенческого семинара (2 -й семестр, много +) - контрольные опросы: плановые и по пропущенным занятиям (-) - обязательные задачи, контрольные решения задач (-) 4. В конце 1 -го семестра - экзамен. Условие допуска - "автомат" или "неавтомат" по результатам работы. 5. В конце 2 -го семестра -экзамен. Возможен "автомат"

1 -й семестр 1) Структура кристаллов – операции и элементы симметрии. Введение в теорию групп. Тензоры 2) Динамика кристаллической решетки (тепловые свойства) 3) Введение в электродинамику сплошных сред (электрические и оптические свойства с точки зрения классической теории)

2 -й семестр 1) Электроны в периодическом поле решетки. Металлы – диэлектрики – полупроводники (основы зонной теории) 2) Электронные и оптические свойства (с точки зрения квантовой теории) 3) Введение в физику гетероструктур и наноструктур 4) Магнитные свойства твердых тел

Структура кристаллов Характерная особенность твердых тел при относительно низких температурах – атомы в них совершают лишь малые колебания около некоторых положений равновесия – “узлов” кристаллической решетки. Взаимное расположение узлов, соответствующее тепловому равновесию тела, является избранным, т. е. выделенным среди других возможных распределений. Термодинамически более выгодным являются более симметричные, периодические расположения атомов. Это расположение определяется симметрийными свойствами атомов и межатомных связей. Для некоторых “материалов” может быть несколько выделенных квазиравновесных расположений узлов. Например, углерод кристаллизуется как алмаз или графит в зависимости от способа кристаллизации. В природе существуют также аморфные твердые тела, в которых атомы колеблются вокруг хаотически расположенных точек. С термодинамической точки зрения такие тела метастабильны и рано или поздно должны были бы закристаллизоваться, однако практически времена релаксации могут быть неограниченно долгими. Таким твердым телом, является, например, стекло, представляющее собой переохлажденную жидкость.

Определение: Идеальный кристалл это тело, состоящее из атомов, расположенных в пространственной решетке так, что можно ввести три вектора а 1, а 2 и а 3, не лежащие в одной плоскости, которые обладают следующим свойством. При рассмотрении этой решетки из произвольной точки r решетка имеет тот же вид, что и при рассмотрении из точки r’: - произвольные целые числа. вектора а 1, а 2 и а 3 -основные вектора решетки В этом определении мы отвлекаемся от тепловых колебаний атомов и наличия поверхностей.

Трансляция Операция перемещения кристалла на вектор - вектор трансляции. Кристалл обладает трансляционной симметрией, т. к. при перемещении на любой вектор трансляции он совмещается сам с собой. определение: Элементарная ячейка - Параллелепипед, образованный векторами основных трансляций а 1, а 2 и а 3. Элементарную ячейку можно выбрать разными способами определение: Примитивная ячейка – элементарная ячейка минимального объема, а соответствующие вектора а 1, а 2 и а 3 – примитивные вектора трансляций. Примитивную ячейку тоже можно выбрать разными способами.

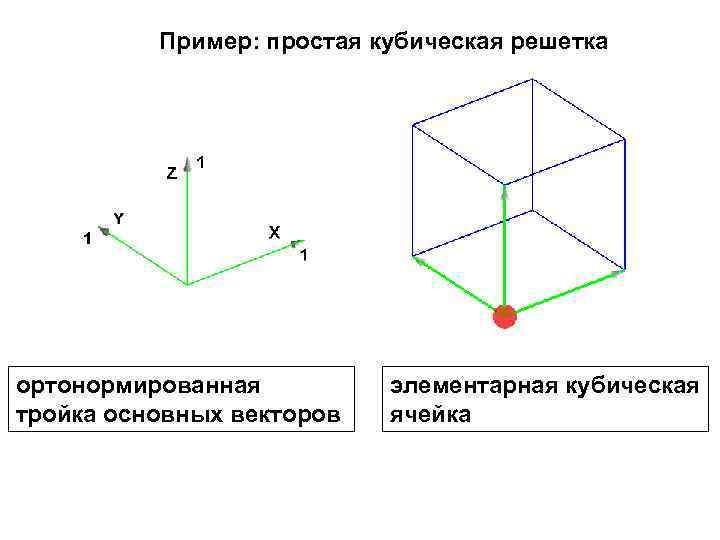
Пример: простая кубическая решетка ортонормированная тройка основных векторов элементарная кубическая ячейка

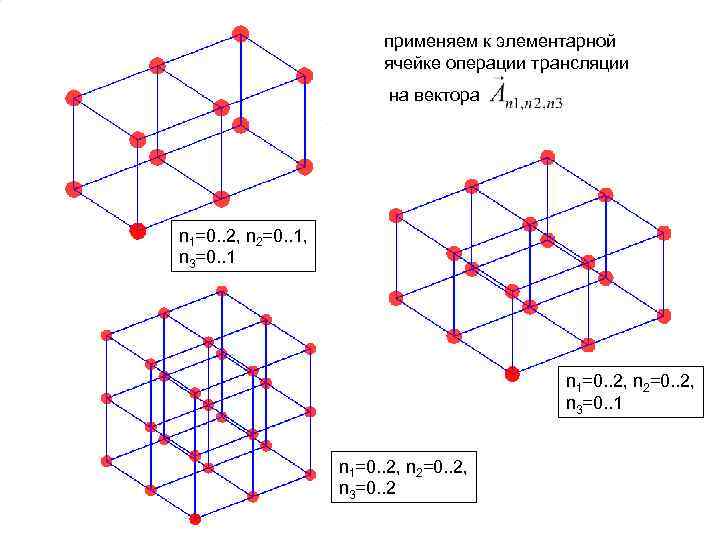
применяем к элементарной ячейке операции трансляции на вектора n 1=0. . 2, n 2=0. . 1, n 3=0. . 1 n 1=0. . 2, n 2=0. . 2, n 3=0. . 2

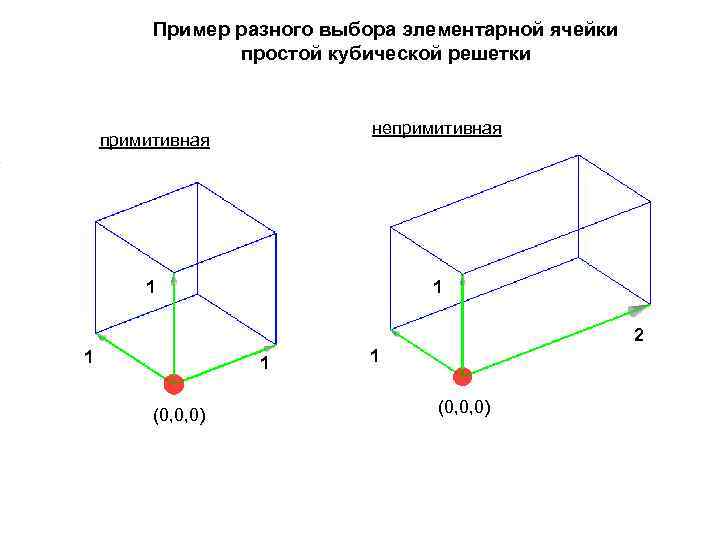
Пример разного выбора элементарной ячейки простой кубической решетки непримитивная 1 1 2 1 1 (0, 0, 0)

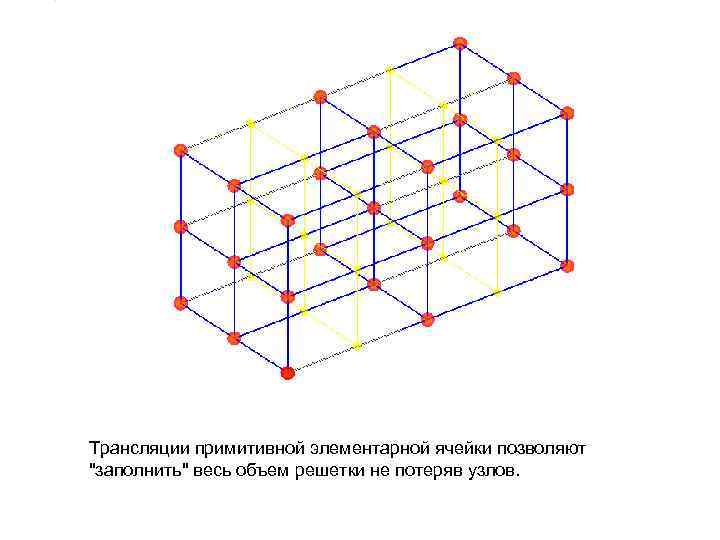
Трансляции примитивной элементарной ячейки позволяют "заполнить" весь объем решетки не потеряв узлов.

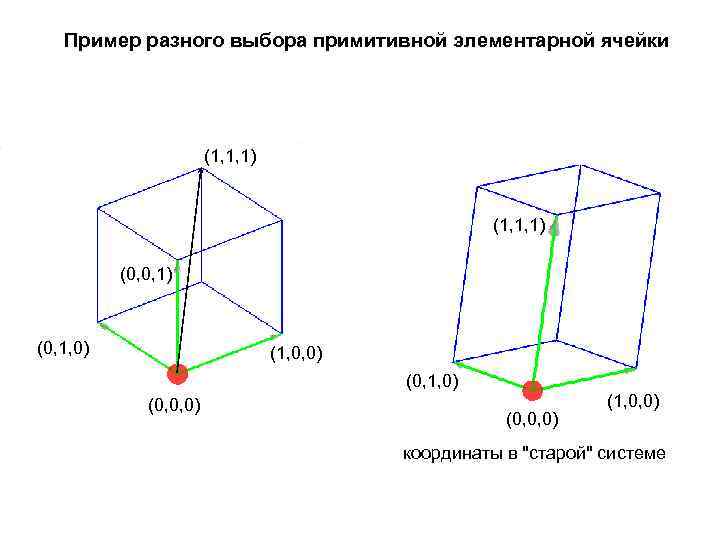
Пример разного выбора примитивной элементарной ячейки (1, 1, 1) (0, 0, 1) (0, 1, 0) (1, 0, 0) (0, 1, 0) (0, 0, 0) (1, 0, 0) координаты в "старой" системе

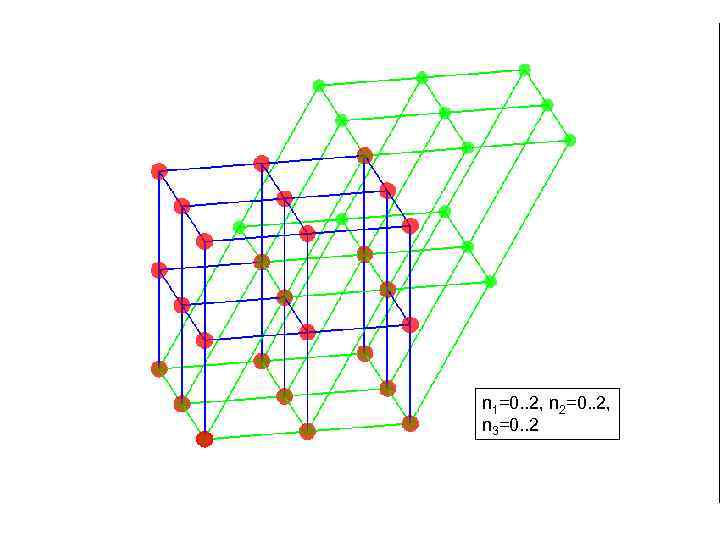
n 1=0. . 2, n 2=0. . 2, n 3=0. . 2

Приведенный пример отвечал случаю простой кубической решетки, реальные кристаллы могут быть много сложнее. (1/2, 1/2) (0, 0, 0) элементарная ячейка с базисом

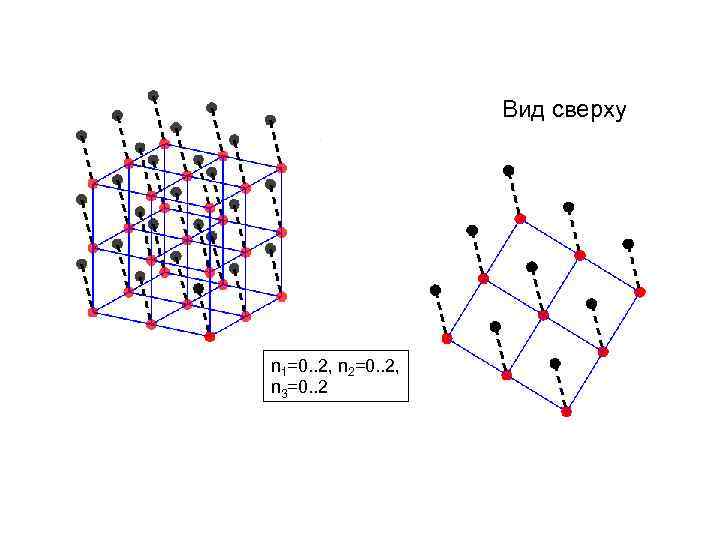
Вид сверху n 1=0. . 2, n 2=0. . 2, n 3=0. . 2

Примитивная ячейка сложной кристаллической решетки – это периодически повторяющаяся в пространстве часть кристаллической решетки, имеющая форму параллелепипеда (наименьшего объема), с которой связана совокупность атомов, называемая базисом. Т. о. базис повторяется в пространстве и образует кристаллическую структуру. Для описания базиса обычно вводят “кристаллографическую” систему координат, сформированную основными векторами трансляций. Тогда координаты узлов в базисе всегда будут меньше 1. определение Пусть а 1, а 2 и а 3 – примитивные вектора трансляций. Возьмем произвольную точку в пространстве и с помощью трансляций этой точки на вектор где n 1, n 2, n 3 пробегают все целые числа, получим пространственную решетку, состоящую из точек. Все узлы такой решетки эквивалентны, т. е. имеют одинаковое окружение. Это решетка Браве – пространственная решетка, построенная на основных примитивных векторах трансляций.

решетка Браве полностью определяет трансляционную симметрию кристалла. Простая кристаллическая решетка имеет базис, состоящий из одного атома. В этом случае все атомы расположены в узлах одной и той же решетки Браве. Если базис содержит несколько атомов, то решетка называется сложной. В этом случае невозможно выбрать примитивную ячейку таким образом, чтобы ей соответствовал лишь один атом. Каждому атому базиса соответствует подрешетка однотипных атомов, идентичная решетке Браве всего кристалла. Различные атомы базиса в сложной решетке не однотипны, даже если это атомы одного и того же элемента, т. к. у них разное окружение. Атомы кристалла однотипны, если они химически идентичны и с каждого из них видна одна и та же картина кристаллической решетки.

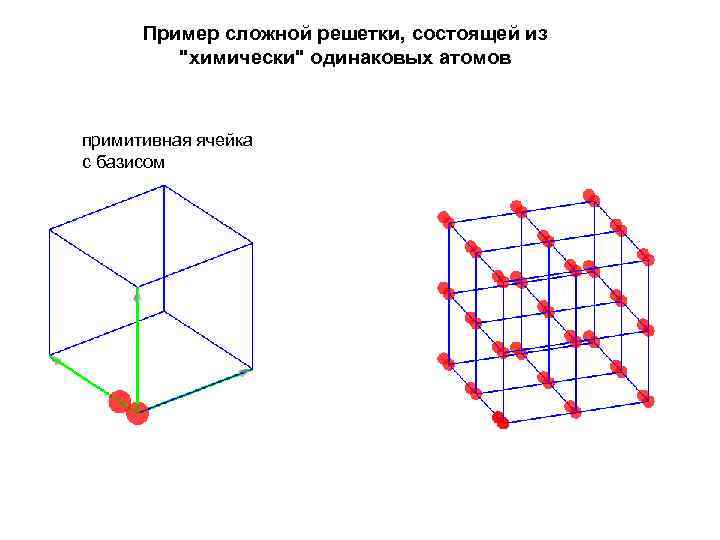
Пример сложной решетки, состоящей из "химически" одинаковых атомов примитивная ячейка с базисом

Увидеть решетку Бравэ можно, если смотреть только на однотипные атомы. Таким образом, построение любого кристалла можно представить двумя способами: 1) Многократно транслируем базис с помощью примитивных основных векторов трансляций. 2) Берем несколько решеток Браве и вставляем их друг в друга. Решетка Браве – математическая абстракция! Кристаллическая структура = решетка Браве + базис

Контрольные вопросы 1. Что мы понимаем под понятием "идеальный кристалл"? 2. Определение операции трансляции 3. Какое твердое тело обладает трансляционной симметрией? 4. Как определяются "элементарная" и "примитивная" ячейка кристаллической решетки? 5. Чем отличаются "простая" и "сложная" кристаллические решетки? 6. Что такое решетка Браве? 7. Может ли сложная кристаллическая решетка состоять из химически одинаковых атомов? 8. Какие атомы кристалла называются однотипными?

Скачать презентацию Физика твердого тела СПб ГПУ ФТФ 2012 -2013

l1_2012_09_05.ppt

Количество слайдов: 30