Lecture 04.ppt
- Количество слайдов: 86
 Физика твердого тела
Физика твердого тела
 Пространственные группы симметрии.
Пространственные группы симметрии.
 1. Элементы симметрии с переносом. Винтовая ось – элемент симметрии осуществляющий поворот на угол: 2 /N (N=2, 3, 4, 6) и одновременный перенос вдоль оси на долю трансляции: t = m/N (m=1, …, N-1) Обозначение: Nm или L Nm
1. Элементы симметрии с переносом. Винтовая ось – элемент симметрии осуществляющий поворот на угол: 2 /N (N=2, 3, 4, 6) и одновременный перенос вдоль оси на долю трансляции: t = m/N (m=1, …, N-1) Обозначение: Nm или L Nm
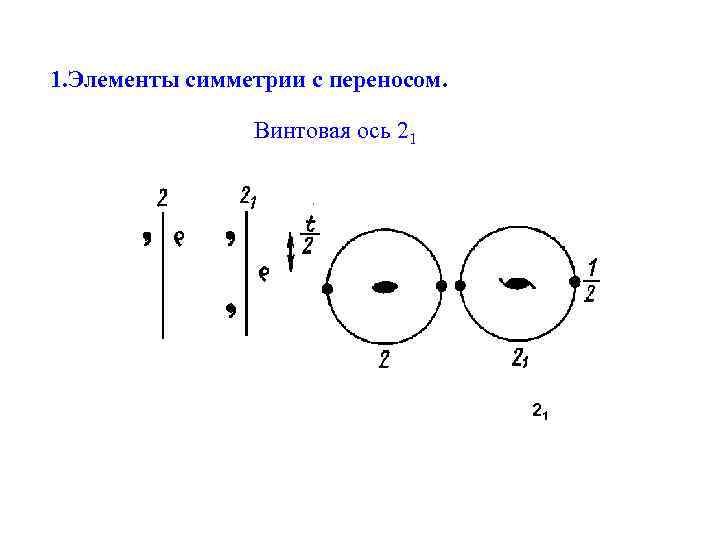 1. Элементы симметрии с переносом. Винтовая ось 21 21
1. Элементы симметрии с переносом. Винтовая ось 21 21
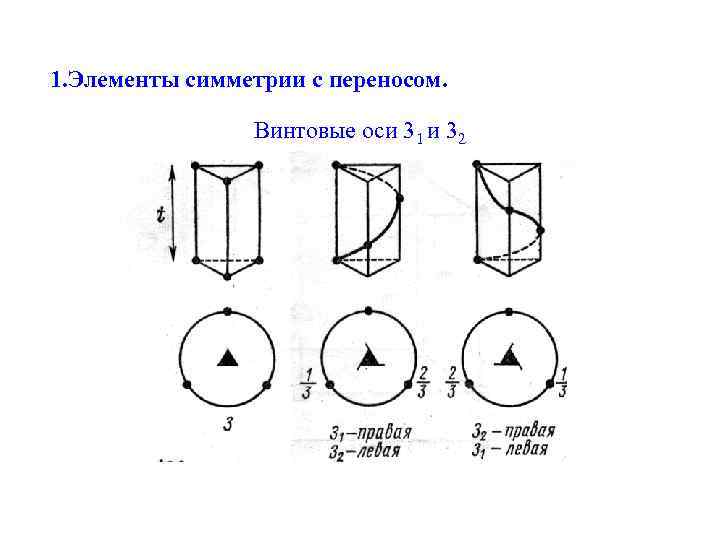 1. Элементы симметрии с переносом. Винтовые оси 31 и 32 21
1. Элементы симметрии с переносом. Винтовые оси 31 и 32 21
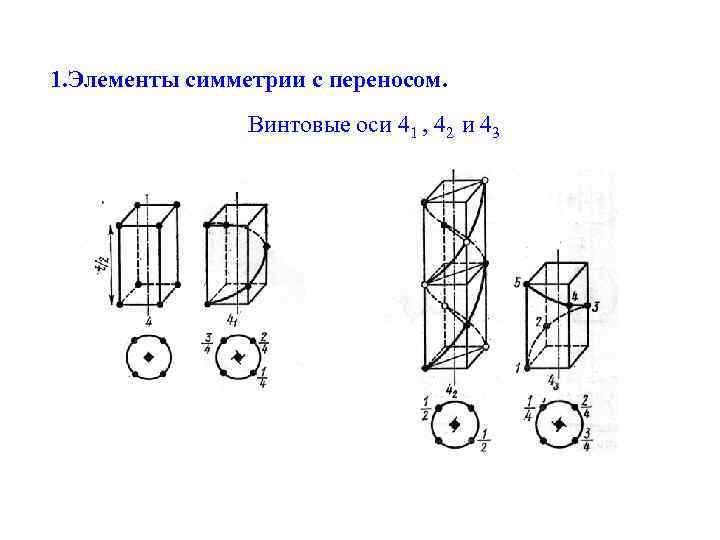 1. Элементы симметрии с переносом. Винтовые оси 41 , 42 и 43
1. Элементы симметрии с переносом. Винтовые оси 41 , 42 и 43
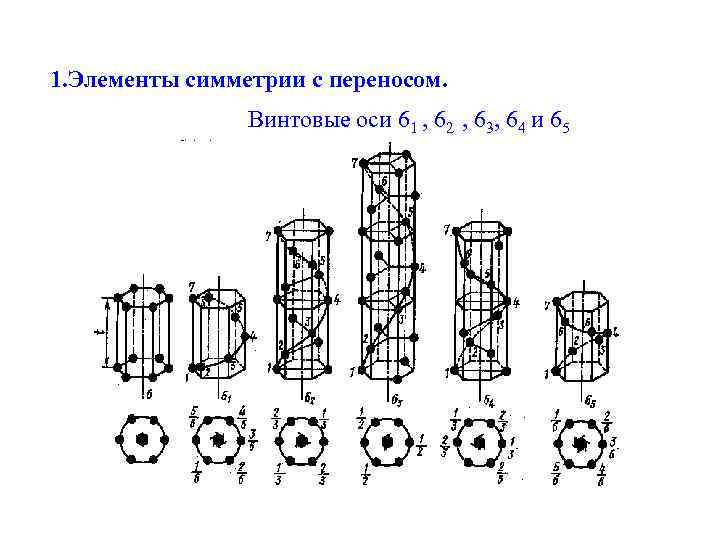 1. Элементы симметрии с переносом. Винтовые оси 61 , 62 , 63, 64 и 65
1. Элементы симметрии с переносом. Винтовые оси 61 , 62 , 63, 64 и 65
 Элементы симметрии с переносом. Плоскости скользящего отражения – элемент симметрии Осуществляющий двойное действие: отражение и перенос вдоль плоскости на величину: a/2 - a , b/2 - b, c/2 - c, (a+b)/2 - n, (a+c)/2 - n, (b+c)/2 – n.
Элементы симметрии с переносом. Плоскости скользящего отражения – элемент симметрии Осуществляющий двойное действие: отражение и перенос вдоль плоскости на величину: a/2 - a , b/2 - b, c/2 - c, (a+b)/2 - n, (a+c)/2 - n, (b+c)/2 – n.
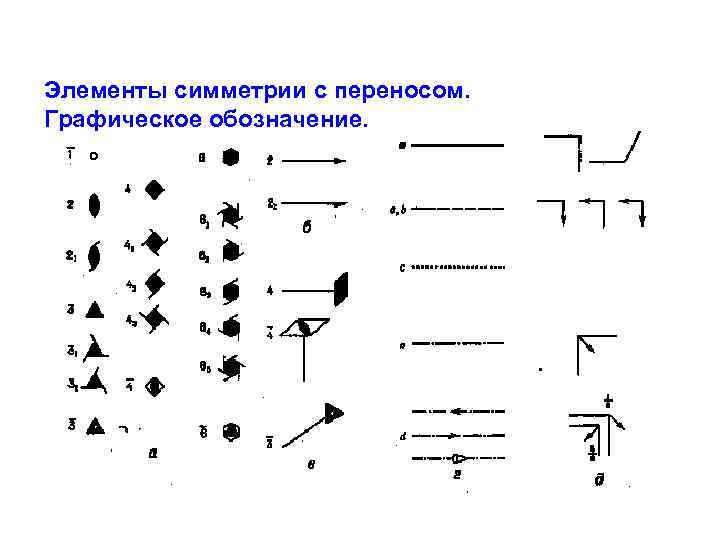 Элементы симметрии с переносом. Графическое обозначение.
Элементы симметрии с переносом. Графическое обозначение.
 Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 1. m //m t Последовательное отражение в двух параллельных плоскостях симметрии равносильно трансляции величиной 2 а, где а – расстояние между плоскостями. Обратная теорема: любую трансляцию можно заменить отражением в двух плоскостях.
Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 1. m //m t Последовательное отражение в двух параллельных плоскостях симметрии равносильно трансляции величиной 2 а, где а – расстояние между плоскостями. Обратная теорема: любую трансляцию можно заменить отражением в двух плоскостях.
 Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 2. t m m Плоскость симметрии и перпендикулярная ей трансляция величиной t порождают новые вставленные плоскости симметрии, параллельные порождающей, аналогичные по типу и отстающие от нее на расстоянии t/2.
Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 2. t m m Плоскость симметрии и перпендикулярная ей трансляция величиной t порождают новые вставленные плоскости симметрии, параллельные порождающей, аналогичные по типу и отстающие от нее на расстоянии t/2.
 Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 3. m t( ) a Плоскость симметрии и трансляция t, составляющая с плоскостью угол , порождают плоскость скользящего отражения, параллельную исходной плоскости и отстоящую от нее на (1/2)t sin и величиной скольжения t cos
Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 3. m t( ) a Плоскость симметрии и трансляция t, составляющая с плоскостью угол , порождают плоскость скользящего отражения, параллельную исходной плоскости и отстоящую от нее на (1/2)t sin и величиной скольжения t cos
 Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 4 a. m a 2 Т 4 б. m c 21 Т 4 в. с с 2 Т 4 г. а c 21 Отражение в двух пересекающихся плоскостях симметрии можно заменить вращением вокруг линии пересечения (или параллельной ей). Обратная теорема: любую ось можно заменить парой соответствующих плоскостей.
Теоремы взаимодействия трансляционных и конечных элементов симметрии. Т 4 a. m a 2 Т 4 б. m c 21 Т 4 в. с с 2 Т 4 г. а c 21 Отражение в двух пересекающихся плоскостях симметрии можно заменить вращением вокруг линии пересечения (или параллельной ей). Обратная теорема: любую ось можно заменить парой соответствующих плоскостей.
 Теоремы взаимодействия трансляционных и конечных элементов симметрии. Трансляция, перпендикулярная оси, Т 5. t Nm Nm порождает такую же ось симметрии, параллельную исходной и смещенную на t/2 в направлении трансляции. Применима ко всем осям, включая -1.
Теоремы взаимодействия трансляционных и конечных элементов симметрии. Трансляция, перпендикулярная оси, Т 5. t Nm Nm порождает такую же ось симметрии, параллельную исходной и смещенную на t/2 в направлении трансляции. Применима ко всем осям, включая -1.
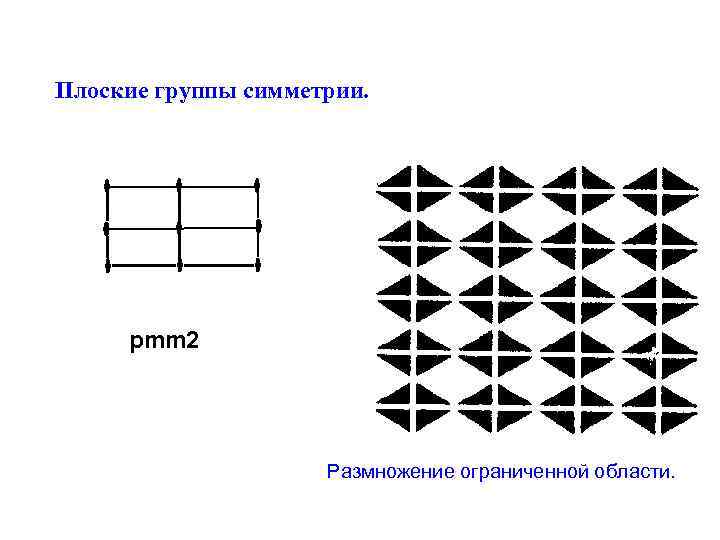 Плоские группы симметрии. pmm 2 Размножение ограниченной области.
Плоские группы симметрии. pmm 2 Размножение ограниченной области.
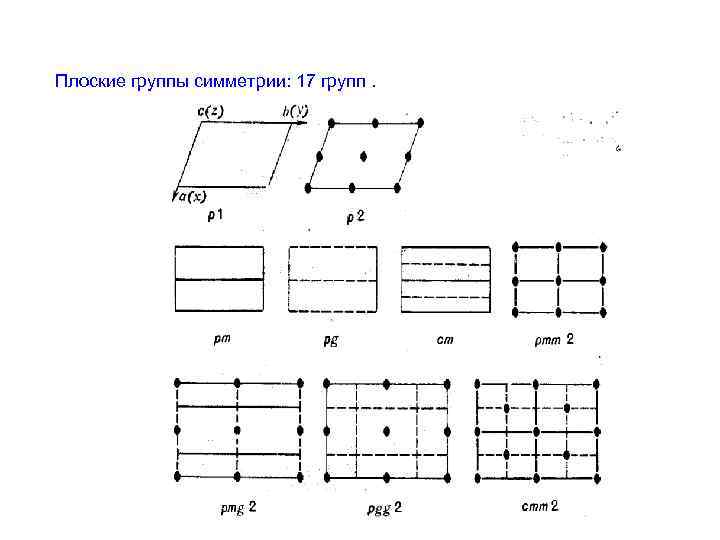 Плоские группы симметрии: 17 групп.
Плоские группы симметрии: 17 групп.
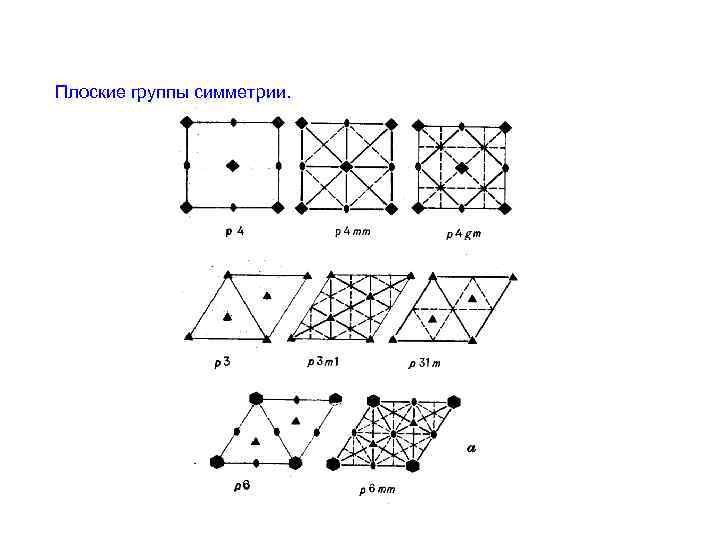 Плоские группы симметрии.
Плоские группы симметрии.
 Правильные системы точек плоских групп симметрии
Правильные системы точек плоских групп симметрии
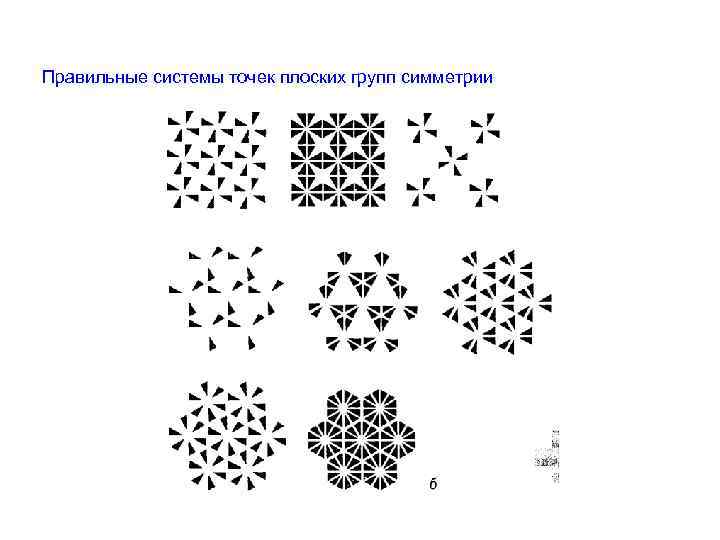 Правильные системы точек плоских групп симметрии
Правильные системы точек плоских групп симметрии
 Распределение пространственных групп симметрии по сингониям Триклинная Моноклинная Ромбическая Тетрагональная Тригональная Гексагональная Кубическая 2 13 59 68 25 27 39 Всего: 230 Выведены Е. С. Федоровым и А. Шенфлисом в период с 1890 по 1894 год.
Распределение пространственных групп симметрии по сингониям Триклинная Моноклинная Ромбическая Тетрагональная Тригональная Гексагональная Кубическая 2 13 59 68 25 27 39 Всего: 230 Выведены Е. С. Федоровым и А. Шенфлисом в период с 1890 по 1894 год.
 Правильная система точек –совокупность симметрично эквивалентных позиций, связанных преобразованиями симметрии пространственной группы. Кратность правильной системы точек – число симметрично эквивалентных точек. Возможные кратности: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48, 96, 192. Частная правильная система точек –получается в том случае, если исходная точка лежит на элементе симметрии. Связь кратности ПСT с химической формулой: Атомы размещаются по различным ПТС пр. группы в соответствии с их кратностью и стехиометрией хим. соединения
Правильная система точек –совокупность симметрично эквивалентных позиций, связанных преобразованиями симметрии пространственной группы. Кратность правильной системы точек – число симметрично эквивалентных точек. Возможные кратности: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48, 96, 192. Частная правильная система точек –получается в том случае, если исходная точка лежит на элементе симметрии. Связь кратности ПСT с химической формулой: Атомы размещаются по различным ПТС пр. группы в соответствии с их кратностью и стехиометрией хим. соединения
 Принятые обозначение точек правильной системы а. Исходная точка; б. Зеркально симметричная точка; в. Точка, находящаяся над плоскостью; г. Точка, находящаяся над плоскостью на расстоянии ½ периода трансляции; д. Две точки: одна над другой.
Принятые обозначение точек правильной системы а. Исходная точка; б. Зеркально симметричная точка; в. Точка, находящаяся над плоскостью; г. Точка, находящаяся над плоскостью на расстоянии ½ периода трансляции; д. Две точки: одна над другой.
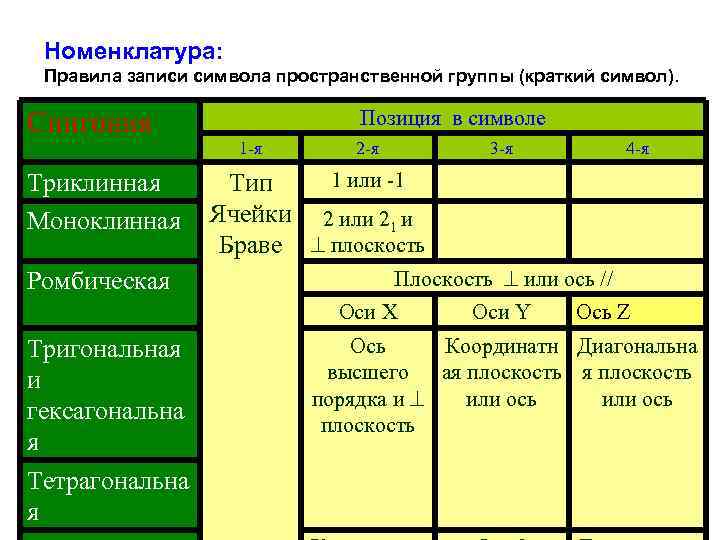 Номенклатура: Правила записи символа пространственной группы (краткий символ). Сингония Триклинная Моноклинная Ромбическая Позиция в символе 1 -я 2 -я 3 -я 1 или -1 Тип Ячейки 2 или 21 и Браве плоскость Плоскость или ось // Оси X Тригональная и гексагональна я Тетрагональна я 4 -я Оси Y Ось Z Ось Координатн Диагональна высшего ая плоскость порядка и или ось плоскость
Номенклатура: Правила записи символа пространственной группы (краткий символ). Сингония Триклинная Моноклинная Ромбическая Позиция в символе 1 -я 2 -я 3 -я 1 или -1 Тип Ячейки 2 или 21 и Браве плоскость Плоскость или ось // Оси X Тригональная и гексагональна я Тетрагональна я 4 -я Оси Y Ось Z Ось Координатн Диагональна высшего ая плоскость порядка и или ось плоскость
 Номенклатура: Триклинная Моноклинная Ромбическая Тетрагональная Тригональная Гексагональная Кубическая P 1, P-1 (P 111) P 21 (P 1211), P 2/m (P 1 2/m 1) Pmmm, P 212121. P 4/mmm, P 4 nc R-3, R-3 m P 6/mmm, P 6222 P 23, Fm-3 m
Номенклатура: Триклинная Моноклинная Ромбическая Тетрагональная Тригональная Гексагональная Кубическая P 1, P-1 (P 111) P 21 (P 1211), P 2/m (P 1 2/m 1) Pmmm, P 212121. P 4/mmm, P 4 nc R-3, R-3 m P 6/mmm, P 6222 P 23, Fm-3 m
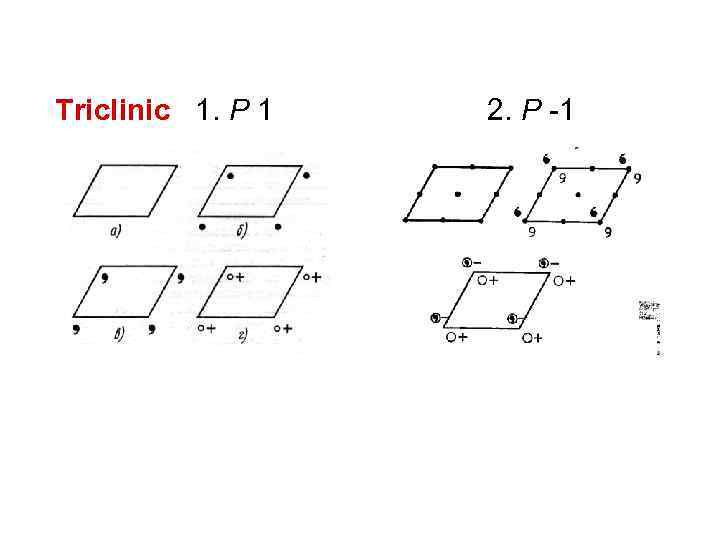 Triclinic 1. P 1 2. P -1
Triclinic 1. P 1 2. P -1
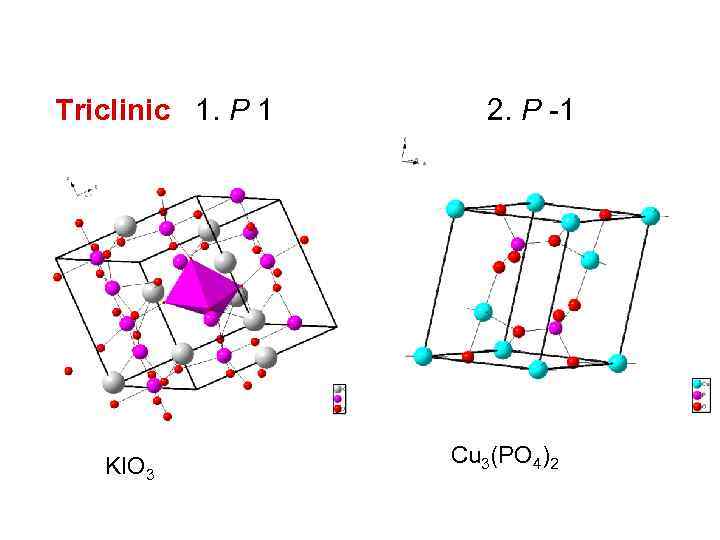 Triclinic 1. P 1 2. P -1 KIO 3 Cu 3(PO 4)2
Triclinic 1. P 1 2. P -1 KIO 3 Cu 3(PO 4)2
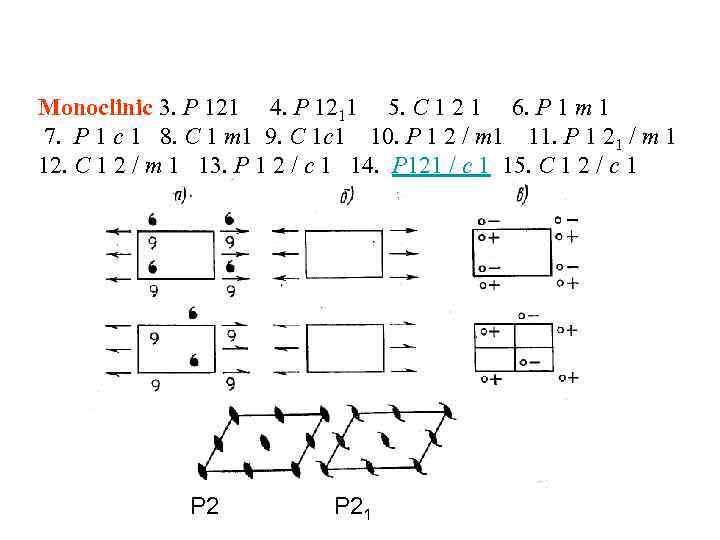 Monoclinic 3. P 121 4. P 1211 5. C 1 2 1 6. P 1 m 1 7. P 1 c 1 8. C 1 m 1 9. C 1 c 1 10. P 1 2 / m 1 11. P 1 21 / m 1 12. C 1 2 / m 1 13. P 1 2 / c 1 14. P 121 / c 1 15. C 1 2 / c 1 P 21
Monoclinic 3. P 121 4. P 1211 5. C 1 2 1 6. P 1 m 1 7. P 1 c 1 8. C 1 m 1 9. C 1 c 1 10. P 1 2 / m 1 11. P 1 21 / m 1 12. C 1 2 / m 1 13. P 1 2 / c 1 14. P 121 / c 1 15. C 1 2 / c 1 P 21
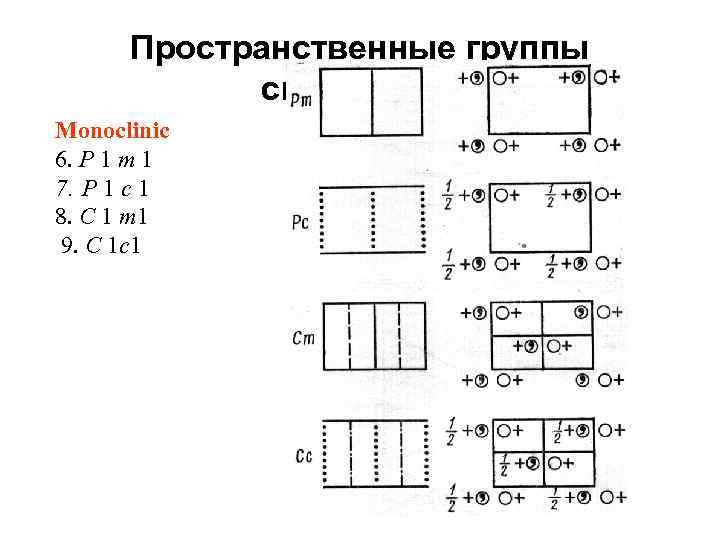 Пространственные группы симметрии. Monoclinic 6. P 1 m 1 7. P 1 c 1 8. C 1 m 1 9. C 1 c 1
Пространственные группы симметрии. Monoclinic 6. P 1 m 1 7. P 1 c 1 8. C 1 m 1 9. C 1 c 1
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
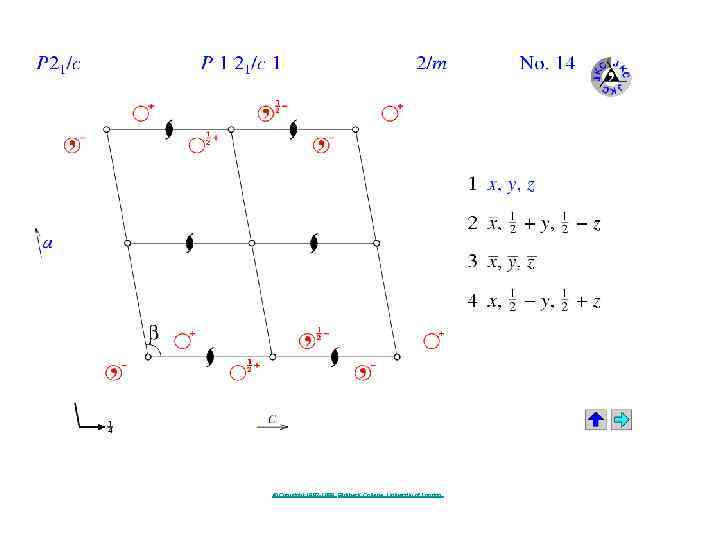
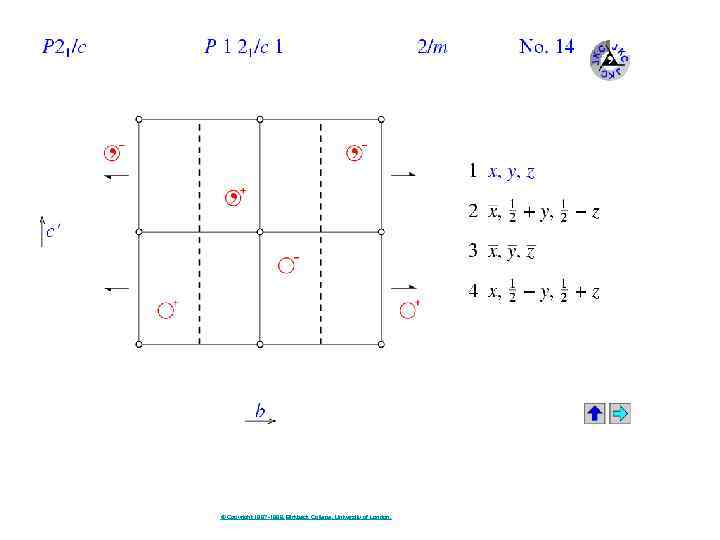
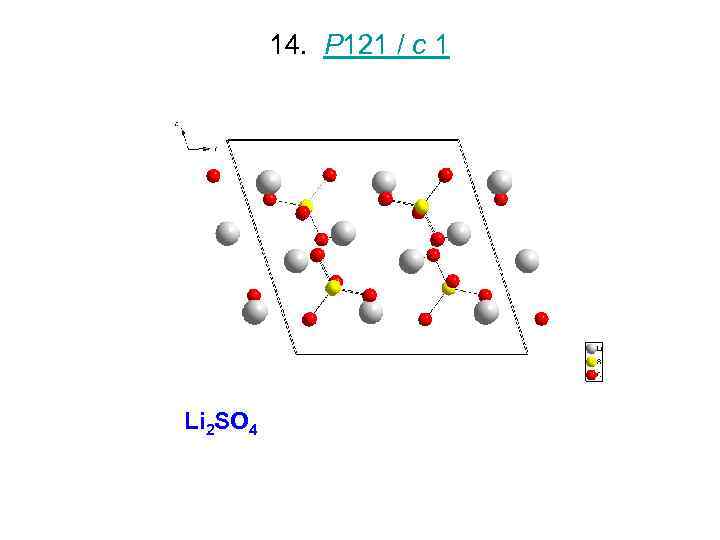 14. P 121 / c 1 Li 2 SO 4
14. P 121 / c 1 Li 2 SO 4
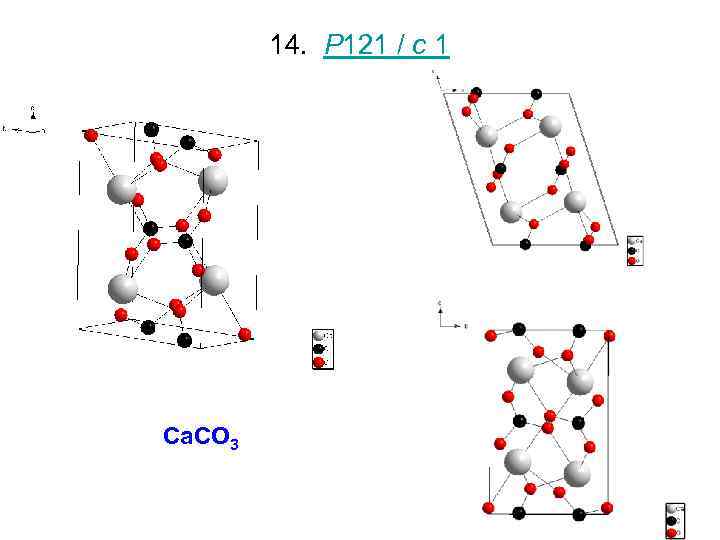 14. P 121 / c 1 Ca. CO 3
14. P 121 / c 1 Ca. CO 3
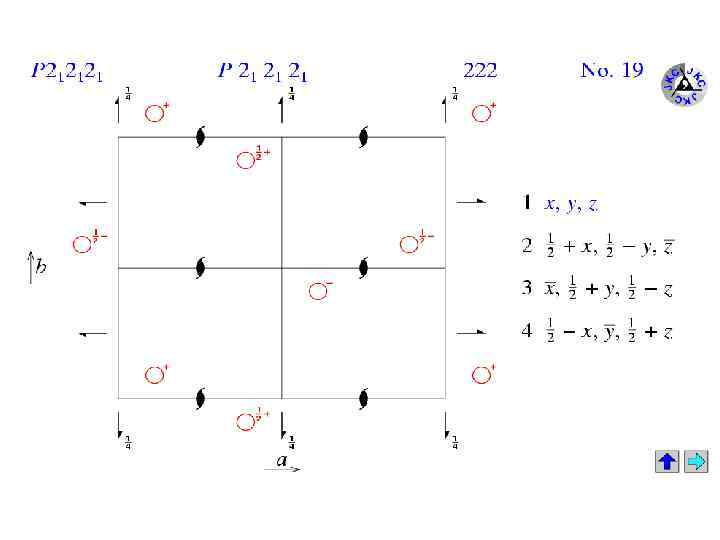
 Orthorhombic 16. P 2 2 2 17. P 2 2 21 18. P 21 21 2 19. P 21 21 21 20. C 2 2 21 21. C 2 22. F 2 23. I 2 24. I 21 21 21 25. P m m 2 26. P m c 21 27. P c c 2 28. P m a 2 29. P c a 21 30. P n c 2 31. P m n 21 32. P b a 2 33. P n a 21 34. P n n 2 35. C m m 2 36. C m c 21 37. C c c 2 38. A m m 2 39. A b m 2 40. A m a 2 41. A b a 2 42. F m m 2 43. F d d 2 44. I m m 2 45. I b a 2 46. I m a 2 47. P m m m 48. P n n n 49. P c c m 50. P b a n 51. P m m a 52. P n n a 53. P m n a 54. P c c a 55. P b a m 56. P c c n 57. P b c m 58. P n n m 59. P m m n 60. P b c n 61. P b c a 62. P n m a 63. C m c m 64. C m c a 65. C m m m 66. C c c m 67. C m m a 68. C c c a 69. F m m m 70. F d d d 71. I m m m 72. I b a m 73. I b c a 74. I m m a
Orthorhombic 16. P 2 2 2 17. P 2 2 21 18. P 21 21 2 19. P 21 21 21 20. C 2 2 21 21. C 2 22. F 2 23. I 2 24. I 21 21 21 25. P m m 2 26. P m c 21 27. P c c 2 28. P m a 2 29. P c a 21 30. P n c 2 31. P m n 21 32. P b a 2 33. P n a 21 34. P n n 2 35. C m m 2 36. C m c 21 37. C c c 2 38. A m m 2 39. A b m 2 40. A m a 2 41. A b a 2 42. F m m 2 43. F d d 2 44. I m m 2 45. I b a 2 46. I m a 2 47. P m m m 48. P n n n 49. P c c m 50. P b a n 51. P m m a 52. P n n a 53. P m n a 54. P c c a 55. P b a m 56. P c c n 57. P b c m 58. P n n m 59. P m m n 60. P b c n 61. P b c a 62. P n m a 63. C m c m 64. C m c a 65. C m m m 66. C c c m 67. C m m a 68. C c c a 69. F m m m 70. F d d d 71. I m m m 72. I b a m 73. I b c a 74. I m m a
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
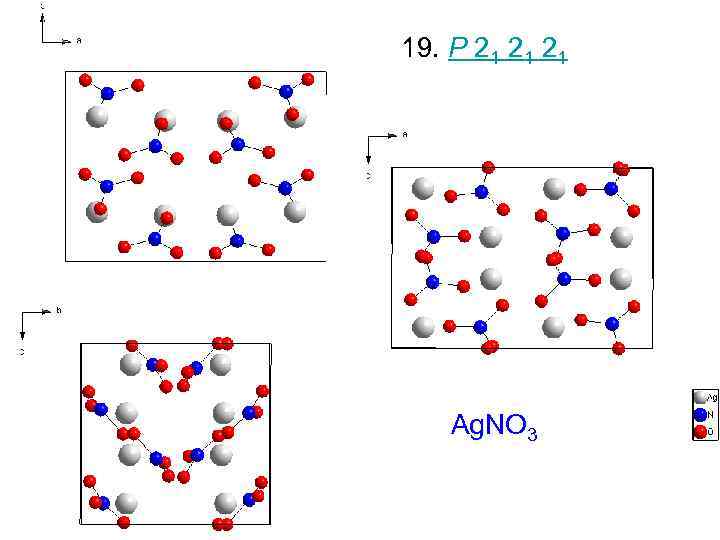 19. P 21 21 21 Ag. NO 3
19. P 21 21 21 Ag. NO 3
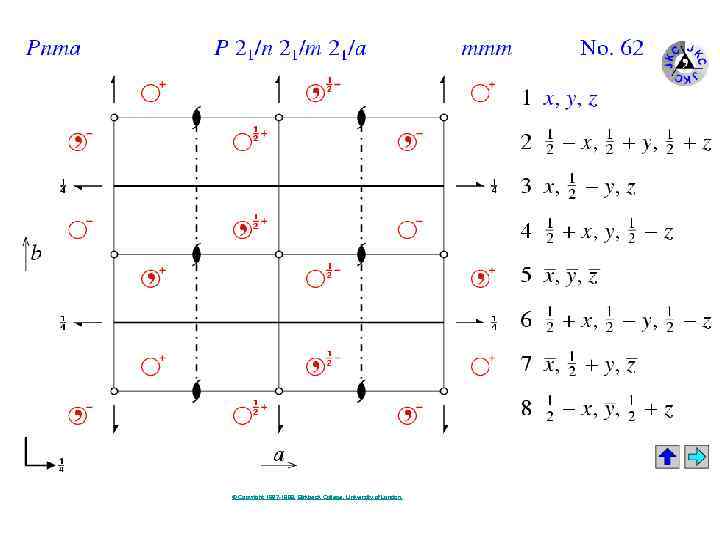 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
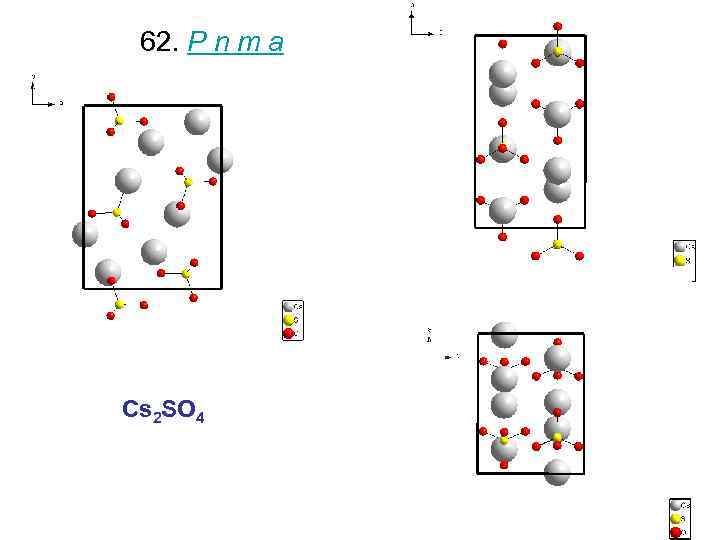 62. P n m a Cs 2 SO 4
62. P n m a Cs 2 SO 4
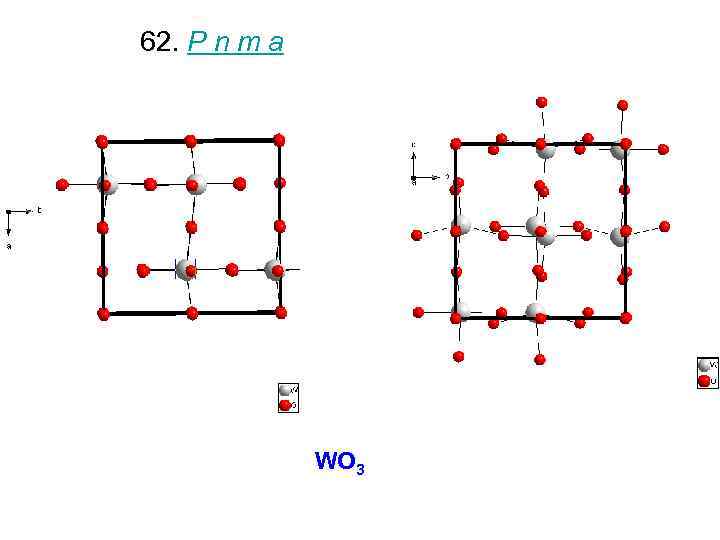 62. P n m a WO 3
62. P n m a WO 3
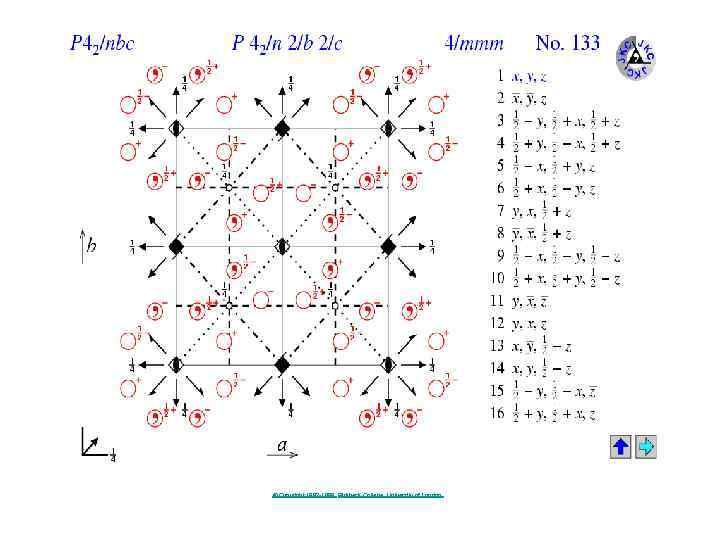
 Tetragonal 75. P 4 76. P 41 77. P 42 78. P 43 79. I 4 80. I 41 81. P -4 82. I -4 83. P 4 / m 84. P 42 / m 85. P 4 / n 86. P 42 / n 87. I 4 / m 88. I 41 / a 89. P 4 2 2 90. P 4 21 2 91. P 41 2 2 92. P 41 21 2 93. P 42 2 2 94. P 42 21 2 95. P 43 2 2 96. P 43 21 2 97. I 4 2 2 98. I 41 2 2 99. P 4 m m 100. P 4 b m 101. P 42 c m 102. P 42 n m 103. P 4 c c 104. P 4 n c 105. P 42 m c 106. P 42 b c 107. I 4 m m 108. I 4 c m 109. I 41 m d 110. I 41 c d 111. P -4 2 m 112. P -4 2 c 113. P -4 21 m 114. P -4 21 c 115. P -4 m 2 116. P -4 c 2 117. P -4 b 2 118. P -4 n 2 119. I -4 m 2 120. I -4 c 2 121. I -4 2 m 122. I -4 2 d 123. P 4 / m m m 124. P 4 / m c c 125. P 4 / n b 127. P 4 / m b 129. P 4 / n m m 126. P 4 / n n c m 128. P 4 / m n c m 131. P 42 / m m 132. P 42 / m c 133. P 42 / n b 134. P 42 / n n 130. P 4 / n c c c m 135. P 42 / m b c 136. P 42 / m n m 137. P 4 / n m c 138. P 4 / n c m 139. I 4 / m m m 2 2 © Copyright 1997 -1999. Birkbeck College, University of London.
Tetragonal 75. P 4 76. P 41 77. P 42 78. P 43 79. I 4 80. I 41 81. P -4 82. I -4 83. P 4 / m 84. P 42 / m 85. P 4 / n 86. P 42 / n 87. I 4 / m 88. I 41 / a 89. P 4 2 2 90. P 4 21 2 91. P 41 2 2 92. P 41 21 2 93. P 42 2 2 94. P 42 21 2 95. P 43 2 2 96. P 43 21 2 97. I 4 2 2 98. I 41 2 2 99. P 4 m m 100. P 4 b m 101. P 42 c m 102. P 42 n m 103. P 4 c c 104. P 4 n c 105. P 42 m c 106. P 42 b c 107. I 4 m m 108. I 4 c m 109. I 41 m d 110. I 41 c d 111. P -4 2 m 112. P -4 2 c 113. P -4 21 m 114. P -4 21 c 115. P -4 m 2 116. P -4 c 2 117. P -4 b 2 118. P -4 n 2 119. I -4 m 2 120. I -4 c 2 121. I -4 2 m 122. I -4 2 d 123. P 4 / m m m 124. P 4 / m c c 125. P 4 / n b 127. P 4 / m b 129. P 4 / n m m 126. P 4 / n n c m 128. P 4 / m n c m 131. P 42 / m m 132. P 42 / m c 133. P 42 / n b 134. P 42 / n n 130. P 4 / n c c c m 135. P 42 / m b c 136. P 42 / m n m 137. P 4 / n m c 138. P 4 / n c m 139. I 4 / m m m 2 2 © Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
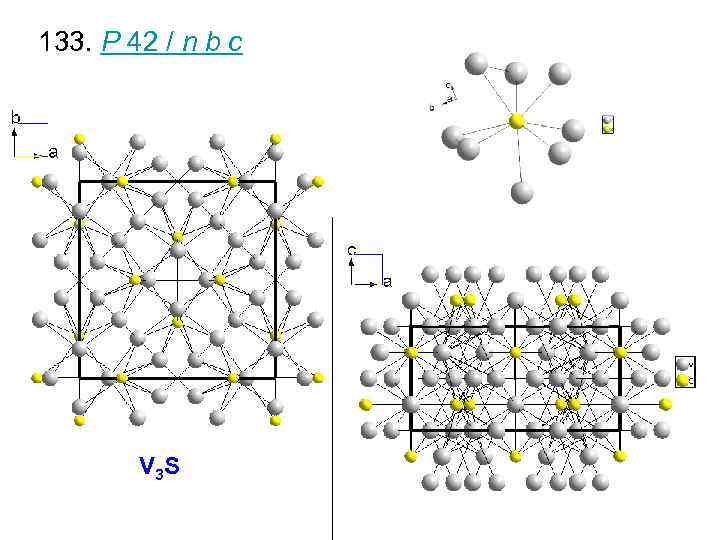 133. P 42 / n b c V 3 S
133. P 42 / n b c V 3 S
 Trigonal 143. P 3 144. P 31 145. P 32 148. R -3 149. P 3 1 2 150. P 3 2 1 146. R 3 147. P -3 151. P 31 1 152. P 31 2 153. P 32 1 154. P 32 2 1 155. R 3 2 2 156. P 3 m 1 157. P 3 1 m 158. P 3 c 1 159. P 3 1 c 161. R 3 c 162. P -3 1 m 160. R 3 m 163. P -3 1 164. P -3 m 165. P -3 c 166. R -3 m 167. R -3 c c 1 1
Trigonal 143. P 3 144. P 31 145. P 32 148. R -3 149. P 3 1 2 150. P 3 2 1 146. R 3 147. P -3 151. P 31 1 152. P 31 2 153. P 32 1 154. P 32 2 1 155. R 3 2 2 156. P 3 m 1 157. P 3 1 m 158. P 3 c 1 159. P 3 1 c 161. R 3 c 162. P -3 1 m 160. R 3 m 163. P -3 1 164. P -3 m 165. P -3 c 166. R -3 m 167. R -3 c c 1 1
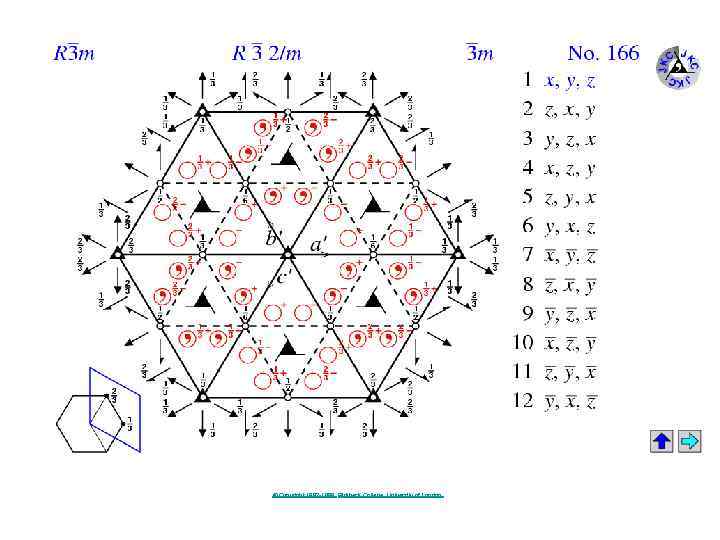 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
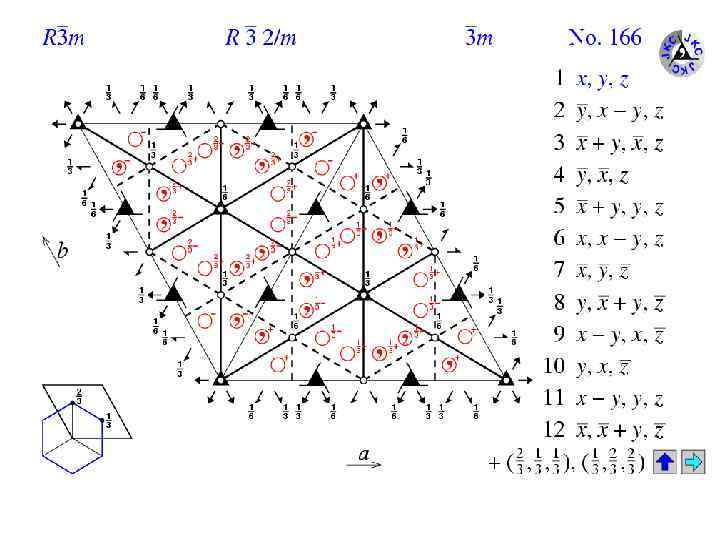 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
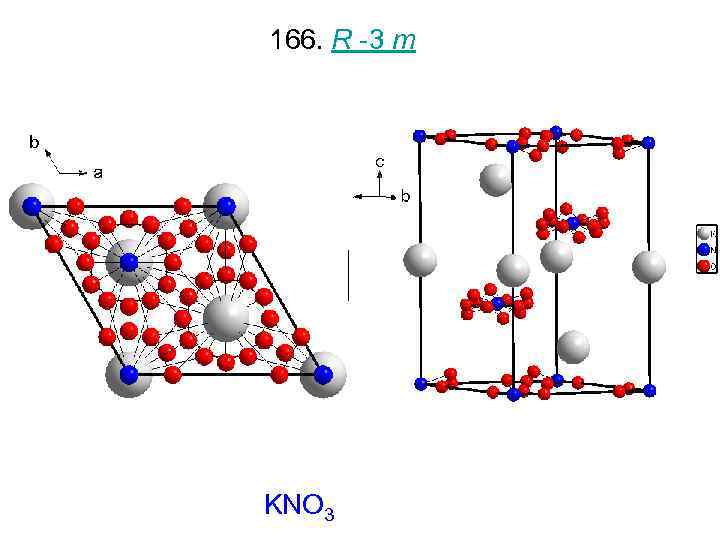 166. R -3 m KNO 3
166. R -3 m KNO 3
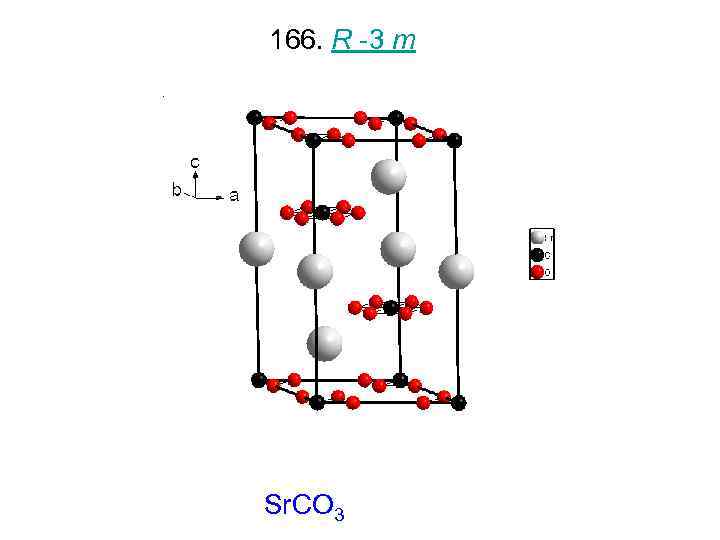 166. R -3 m Sr. CO 3
166. R -3 m Sr. CO 3
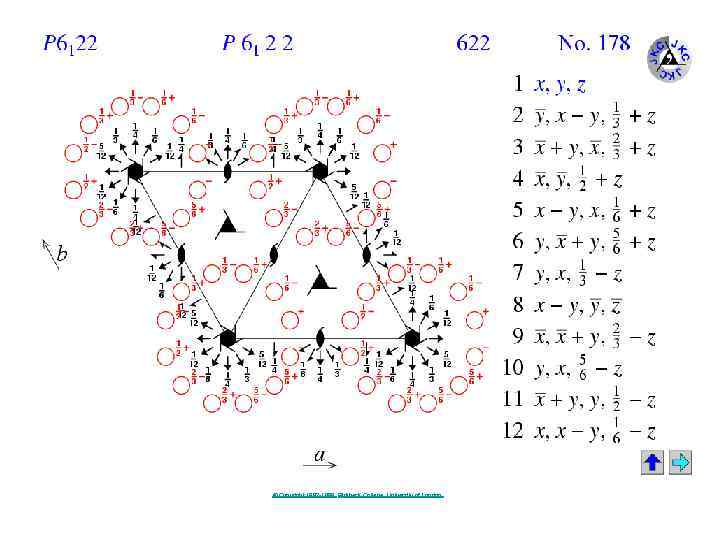
 Hexagonal 168. P 6 169. P 61 170. P 65 171. P 62 172. P 64 173. P 63 174. P -6 175. P 6 / m 176. P 63 / m 177. P 6 2 2 178. P 61 2 2 179. P 65 2 2 180. P 62 2 2 181. P 64 2 2 182. P 63 2 2 183. P 6 m m 184. P 6 c c 185. P 63 c m 186. P 63 m c 187. P -6 m 2 188. P -6 c 2 189. P -6 2 m 190. P -6 2 c 191. P 6 / m m m 192. P 6 / m c c 193. P 63 / m c m 194. P 63 / m m c
Hexagonal 168. P 6 169. P 61 170. P 65 171. P 62 172. P 64 173. P 63 174. P -6 175. P 6 / m 176. P 63 / m 177. P 6 2 2 178. P 61 2 2 179. P 65 2 2 180. P 62 2 2 181. P 64 2 2 182. P 63 2 2 183. P 6 m m 184. P 6 c c 185. P 63 c m 186. P 63 m c 187. P -6 m 2 188. P -6 c 2 189. P -6 2 m 190. P -6 2 c 191. P 6 / m m m 192. P 6 / m c c 193. P 63 / m c m 194. P 63 / m m c
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
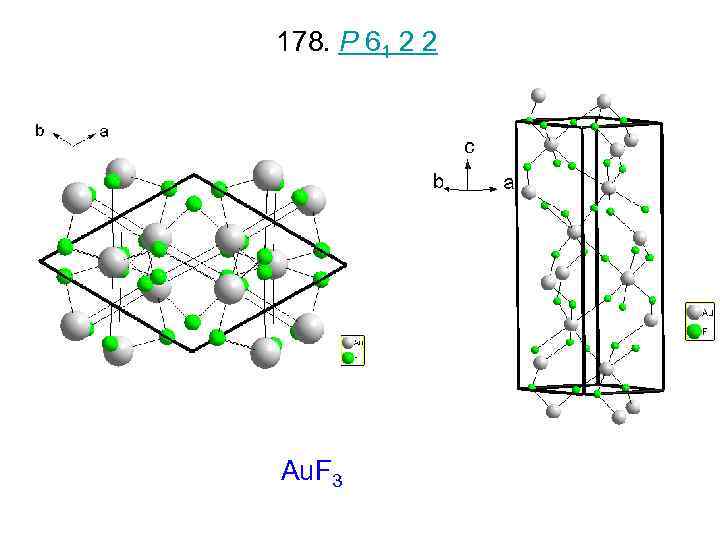 178. P 61 2 2 Au. F 3
178. P 61 2 2 Au. F 3
 Cubic 195. P 2 196. F 2 197. I 2 198. P 3 3 3 21 3 199. I 21 3 200. P m -3 201. P n 202. F -3 m -3 203. F d -3 204. I m -3 205. P a 206. I a 207. P -3 -3 4 3 2 208. P 42 3 2 209. F 4 3 2 210. F 41 3 2 213. P 41 3 2 214. I 41 3 2 211. I 4 212. P 3 2 43 3 2 215. P - 216. F - 217. I - 218. P - 219. F 4 3 m 4 3 n 4 3 c 220. I 4 3 d 221. P m -3 m 222. P n -3 n 223. P m -3 n 224. P n -3 m 225. F m -3 m 226. F m -3 c 227. F d -3 m 228. F d -3 c 229. I m -3 m © Copyright 1997 -1999. Birkbeck College, University of London.
Cubic 195. P 2 196. F 2 197. I 2 198. P 3 3 3 21 3 199. I 21 3 200. P m -3 201. P n 202. F -3 m -3 203. F d -3 204. I m -3 205. P a 206. I a 207. P -3 -3 4 3 2 208. P 42 3 2 209. F 4 3 2 210. F 41 3 2 213. P 41 3 2 214. I 41 3 2 211. I 4 212. P 3 2 43 3 2 215. P - 216. F - 217. I - 218. P - 219. F 4 3 m 4 3 n 4 3 c 220. I 4 3 d 221. P m -3 m 222. P n -3 n 223. P m -3 n 224. P n -3 m 225. F m -3 m 226. F m -3 c 227. F d -3 m 228. F d -3 c 229. I m -3 m © Copyright 1997 -1999. Birkbeck College, University of London.
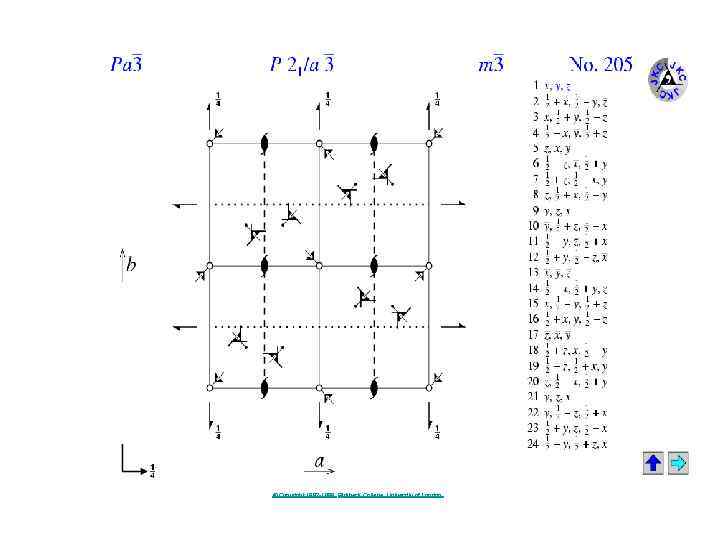 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
 © Copyright 1997 -1999. Birkbeck College, University of London.
© Copyright 1997 -1999. Birkbeck College, University of London.
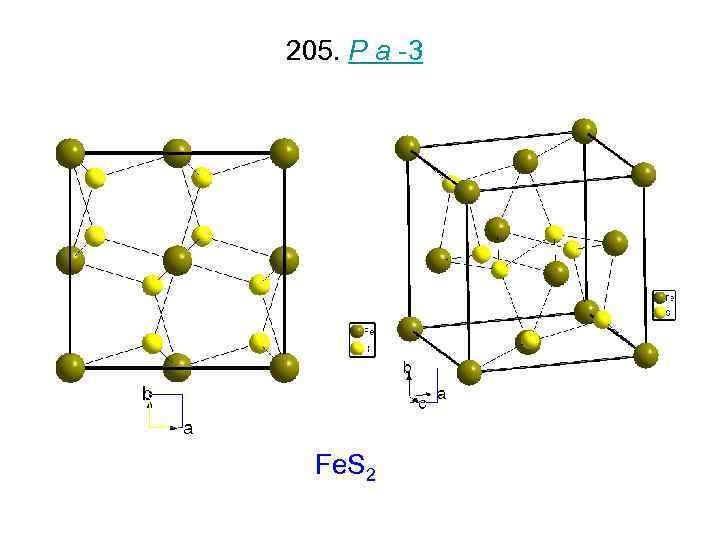 205. P a -3 Fe. S 2
205. P a -3 Fe. S 2
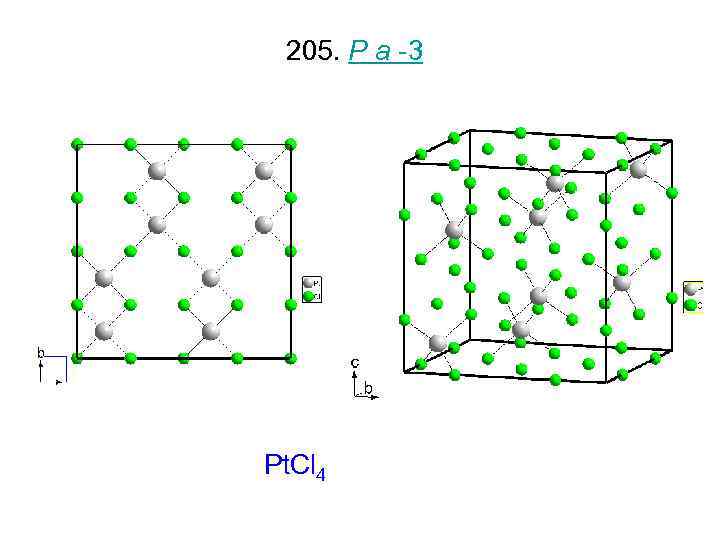 205. P a -3 Pt. Cl 4
205. P a -3 Pt. Cl 4
 Независимая область ячейки – минимальная область, позволяющая путем действия элементов симметрии заполнить все пространство ячейки без перекрывания и промежутков. Определяется неоднозначно. Применяется в структурном анализе при расшифровке структуры и кристаллохимии при сравнительном анализе структур. В независимой области может содержаться целое число формульных единиц либо дробная часть. Независимая область ячейки для структуры Na. Cl. (плоский и объемный вид для 1/8 ячейки
Независимая область ячейки – минимальная область, позволяющая путем действия элементов симметрии заполнить все пространство ячейки без перекрывания и промежутков. Определяется неоднозначно. Применяется в структурном анализе при расшифровке структуры и кристаллохимии при сравнительном анализе структур. В независимой области может содержаться целое число формульных единиц либо дробная часть. Независимая область ячейки для структуры Na. Cl. (плоский и объемный вид для 1/8 ячейки
 Разбиение пространства на фундаментальные области Стереоны- фундаментальные области заполняющие пространство без промежутков. Количество областей в ячейке равно кратности группы. Плоскости и оси симметрии окаймляют область. Плоскогранные стереоны можно построить по методу Дирихле. Для каждой пространственной группы существует большое число топологически различных стереонов, что определяется различным Соотношением параметров ячейки. Форма стереона однозначно характеризует пространственную группу.
Разбиение пространства на фундаментальные области Стереоны- фундаментальные области заполняющие пространство без промежутков. Количество областей в ячейке равно кратности группы. Плоскости и оси симметрии окаймляют область. Плоскогранные стереоны можно построить по методу Дирихле. Для каждой пространственной группы существует большое число топологически различных стереонов, что определяется различным Соотношением параметров ячейки. Форма стереона однозначно характеризует пространственную группу.
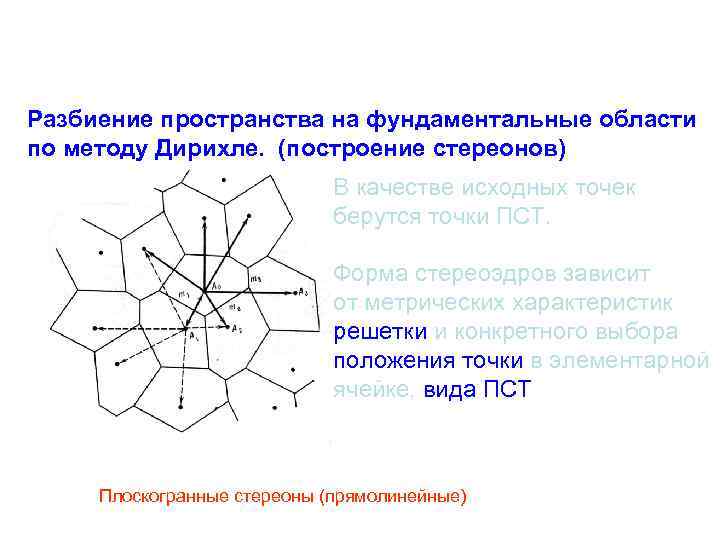 Разбиение пространства на фундаментальные области по методу Дирихле. (построение стереонов) В качестве исходных точек берутся точки ПСТ. Форма стереоэдров зависит от метрических характеристик решетки и конкретного выбора положения точки в элементарной ячейке, вида ПСТ Плоскогранные стереоны (прямолинейные)
Разбиение пространства на фундаментальные области по методу Дирихле. (построение стереонов) В качестве исходных точек берутся точки ПСТ. Форма стереоэдров зависит от метрических характеристик решетки и конкретного выбора положения точки в элементарной ячейке, вида ПСТ Плоскогранные стереоны (прямолинейные)
 Разбиение пространства на фундаментальные области Pnnn P-3 Неплоскогранные стереоны (криволинейные)
Разбиение пространства на фундаментальные области Pnnn P-3 Неплоскогранные стереоны (криволинейные)
 Разбиение пространства на фундаментальные области Наиболее симметричные плоскогранные стереоны (стереоэдры) : Куб, г. призма, ромбододекаэдр, вытя – нутый ромбододекаэдр, кубооктаэдр. Заполнение пространства: 1. Гексагональными призмами. 2. Ромбододекаэдрами 3. Кубооттаэдрами
Разбиение пространства на фундаментальные области Наиболее симметричные плоскогранные стереоны (стереоэдры) : Куб, г. призма, ромбододекаэдр, вытя – нутый ромбододекаэдр, кубооктаэдр. Заполнение пространства: 1. Гексагональными призмами. 2. Ромбододекаэдрами 3. Кубооттаэдрами
 Разбиение пространства на фундаментальные области Построение области Вороного-Дирихле или решетки Вигнера-Зейтца в обратном пространстве: В качестве исходных точек берутся узлы ячейки. Области Дирихле всегда центросимметричны Решетка Вигнера-Зейтца применяется для описания энергетических зон в кристалле.
Разбиение пространства на фундаментальные области Построение области Вороного-Дирихле или решетки Вигнера-Зейтца в обратном пространстве: В качестве исходных точек берутся узлы ячейки. Области Дирихле всегда центросимметричны Решетка Вигнера-Зейтца применяется для описания энергетических зон в кристалле.
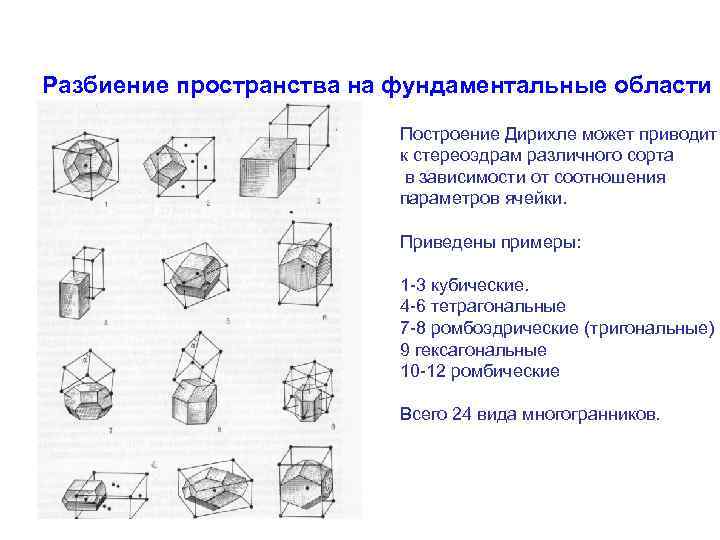 Разбиение пространства на фундаментальные области Построение Дирихле может приводит к стереоэдрам различного сорта в зависимости от соотношения параметров ячейки. Приведены примеры: 1 -3 кубические. 4 -6 тетрагональные 7 -8 ромбоэдрические (тригональные) 9 гексагональные 10 -12 ромбические Всего 24 вида многогранников.
Разбиение пространства на фундаментальные области Построение Дирихле может приводит к стереоэдрам различного сорта в зависимости от соотношения параметров ячейки. Приведены примеры: 1 -3 кубические. 4 -6 тетрагональные 7 -8 ромбоэдрические (тригональные) 9 гексагональные 10 -12 ромбические Всего 24 вида многогранников.
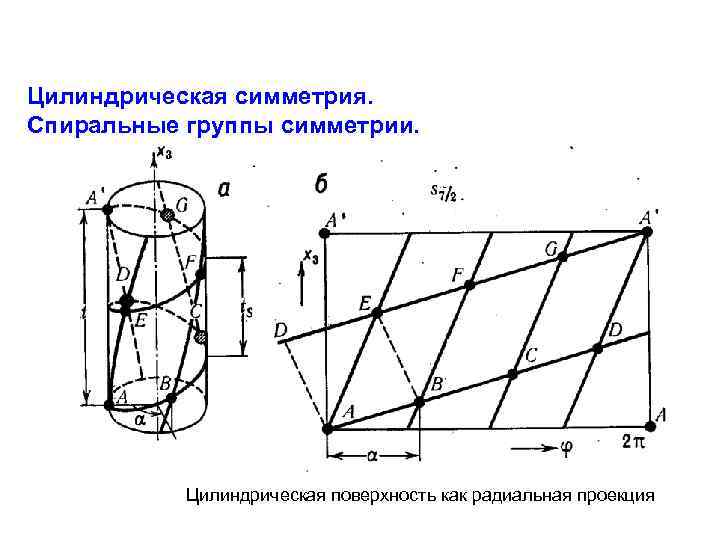 Цилиндрическая симметрия. Спиральные группы симметрии. Цилиндрическая поверхность как радиальная проекция
Цилиндрическая симметрия. Спиральные группы симметрии. Цилиндрическая поверхность как радиальная проекция
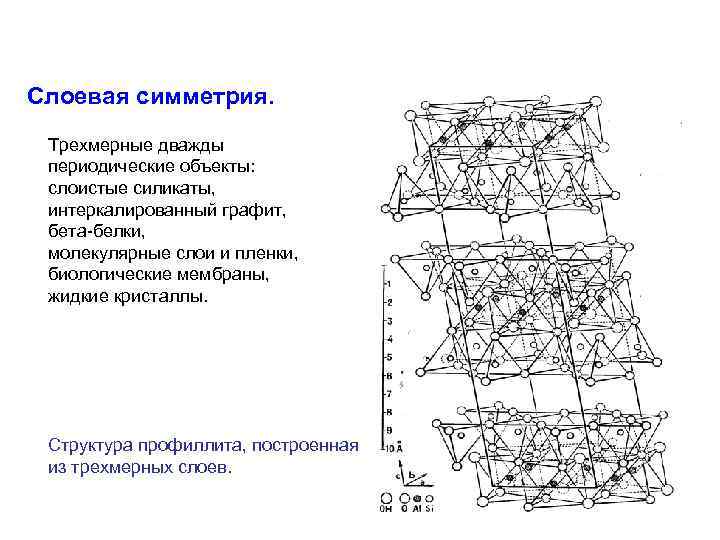 Слоевая симметрия. Трехмерные дважды периодические объекты: слоистые силикаты, интеркалированный графит, бета-белки, молекулярные слои и пленки, биологические мембраны, жидкие кристаллы. Структура профиллита, построенная из трехмерных слоев.
Слоевая симметрия. Трехмерные дважды периодические объекты: слоистые силикаты, интеркалированный графит, бета-белки, молекулярные слои и пленки, биологические мембраны, жидкие кристаллы. Структура профиллита, построенная из трехмерных слоев.
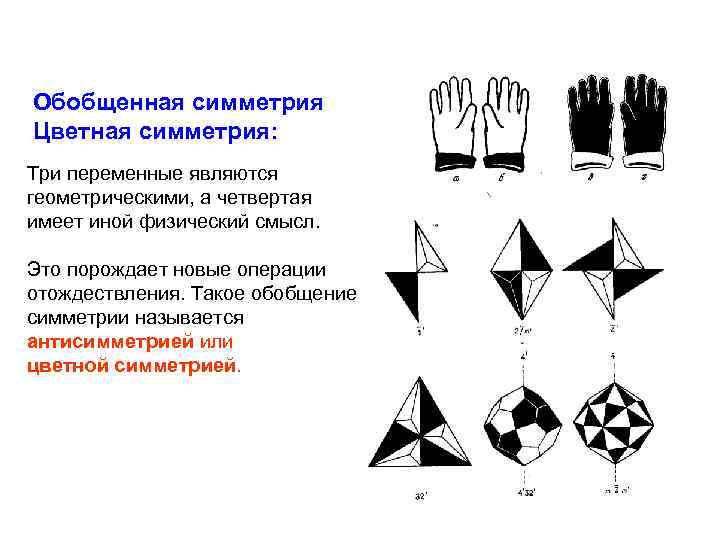 Обобщенная симметрия Цветная симметрия: Три переменные являются геометрическими, а четвертая имеет иной физический смысл. Это порождает новые операции отождествления. Такое обобщение симметрии называется антисимметрией или цветной симметрией.
Обобщенная симметрия Цветная симметрия: Три переменные являются геометрическими, а четвертая имеет иной физический смысл. Это порождает новые операции отождествления. Такое обобщение симметрии называется антисимметрией или цветной симметрией.
 Цветная симметрия:
Цветная симметрия:
 Цветная симметрия:
Цветная симметрия:
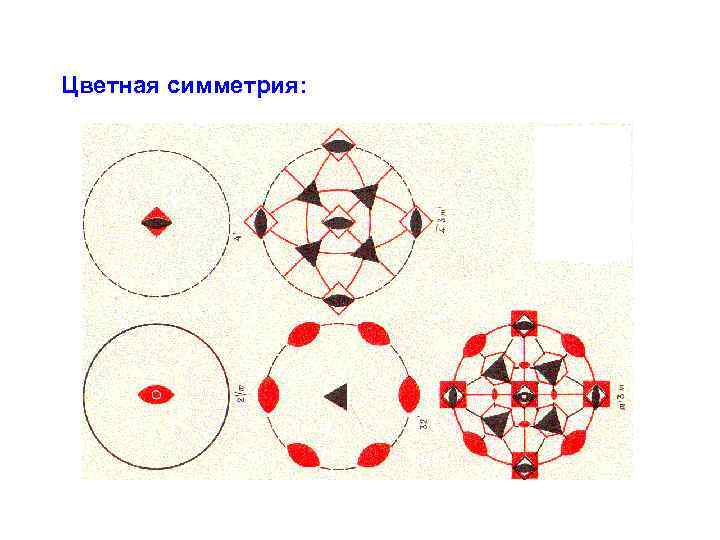 Цветная симметрия:
Цветная симметрия:
 Цветная симметрия:
Цветная симметрия:
 Симметрия подобия. Частичная симметрия. Статистическая симметрия.
Симметрия подобия. Частичная симметрия. Статистическая симметрия.
 Предельные группы симметрии или группы Кюри -точечные группы симметрии, содержащие оси симметрии бесконечного порядка Группы применяются для описания физических сред, когда дискретность не имеет значения. Имеется 7 предельных групп: , m, /m, 2, /mmm, /
Предельные группы симметрии или группы Кюри -точечные группы симметрии, содержащие оси симметрии бесконечного порядка Группы применяются для описания физических сред, когда дискретность не имеет значения. Имеется 7 предельных групп: , m, /m, 2, /mmm, /
 Предельные группы симметрии или группы Кюри Группа , (Одна ось, соответствует симметрии равномерно вращающегося конуса) Группа полярна и энантиоморфна
Предельные группы симметрии или группы Кюри Группа , (Одна ось, соответствует симметрии равномерно вращающегося конуса) Группа полярна и энантиоморфна
 Предельные группы симметрии или группы Кюри Группа m (ось и бесконечное число продольных плоскостей, соответствует покоящемуся конусу) Бесконечное количество продольных плоскостей, Группа полярна, но не энантиаоморфна, Описывает симметрию однородного электрического поля Е.
Предельные группы симметрии или группы Кюри Группа m (ось и бесконечное число продольных плоскостей, соответствует покоящемуся конусу) Бесконечное количество продольных плоскостей, Группа полярна, но не энантиаоморфна, Описывает симметрию однородного электрического поля Е.
 Предельные группы симметрии или группы Кюри Группа /m Ось симметрии (неполярная ) и поперечная плоскость, соответствует вращающемуся цилиндру, Торцы цилиндра неодинаковы. Нет энантиоморфных форм. Описывает симметрию однородного Магнитного поля Н прямолинейного тока.
Предельные группы симметрии или группы Кюри Группа /m Ось симметрии (неполярная ) и поперечная плоскость, соответствует вращающемуся цилиндру, Торцы цилиндра неодинаковы. Нет энантиоморфных форм. Описывает симметрию однородного Магнитного поля Н прямолинейного тока.
 Предельные группы симметрии или группы Кюри Группа 2 Ось симметрии (неполярная ) и бесконечное число поперечных осей 2. Соответствует цилиндру, концы которого закручены в разные стороны. . Описывает симметрию удельного вращения плоскости поляризации света в анизотропной среде. Независимо как смотреть, Вращение остается правым или левым.
Предельные группы симметрии или группы Кюри Группа 2 Ось симметрии (неполярная ) и бесконечное число поперечных осей 2. Соответствует цилиндру, концы которого закручены в разные стороны. . Описывает симметрию удельного вращения плоскости поляризации света в анизотропной среде. Независимо как смотреть, Вращение остается правым или левым.
 Предельные группы симметрии или группы Кюри Группа /mmm Ось симметрии (неполярная ), поперечная плоскость и бесконечное число продольных. Соответствует покоящемуся цилиндру. Описывает симметрию одноосного сжимающего или растягивающего усилия.
Предельные группы симметрии или группы Кюри Группа /mmm Ось симметрии (неполярная ), поперечная плоскость и бесконечное число продольных. Соответствует покоящемуся цилиндру. Описывает симметрию одноосного сжимающего или растягивающего усилия.
 Предельные группы симметрии или группы Кюри Группа / m Центр симметрии и бесконечное множество осей бесконечного порядка. Соответствует симметрии шара. . Описывает симметрию гидростатического сжатия. или однородный нагрев.
Предельные группы симметрии или группы Кюри Группа / m Центр симметрии и бесконечное множество осей бесконечного порядка. Соответствует симметрии шара. . Описывает симметрию гидростатического сжатия. или однородный нагрев.
 Предельные группы симметрии или группы Кюри Группа / Бесконечное множество осей бесконечного порядка (без плоскостей и центра симметрии. Соответствует симметрии шара, у которого все диаметры закручены вправо или влево. Описывает симметрию удельного вращения плоскости поляризации света в анизотропной среде.
Предельные группы симметрии или группы Кюри Группа / Бесконечное множество осей бесконечного порядка (без плоскостей и центра симметрии. Соответствует симметрии шара, у которого все диаметры закручены вправо или влево. Описывает симметрию удельного вращения плоскости поляризации света в анизотропной среде.
 Основные принципы симметрии в кристаллофизике. Принцип Кюри: Если определенные причины вызывают соответствующие следствия, то элементы симметрии причин должны проявляться в вызванных ими следствиях. (обратное не верно, т. е следствия могут обладать белее высокой симметрией, чем причины) Принцип означает, что элементы симметрии кристалла Являются в тоже время элементами симметрии любого физического свойства. (точечная группа физ. свойства включает точечную симметрию самого кристалла. )
Основные принципы симметрии в кристаллофизике. Принцип Кюри: Если определенные причины вызывают соответствующие следствия, то элементы симметрии причин должны проявляться в вызванных ими следствиях. (обратное не верно, т. е следствия могут обладать белее высокой симметрией, чем причины) Принцип означает, что элементы симметрии кристалла Являются в тоже время элементами симметрии любого физического свойства. (точечная группа физ. свойства включает точечную симметрию самого кристалла. )
 Основные принципы симметрии в кристаллофизике. Принцип суперпозиции Кюри: Когда различные внешние воздействия накладываются друг на друга, образуя единую систему, их диссимметрии складываются. В результате остаются лишь общие элементы симметрии.
Основные принципы симметрии в кристаллофизике. Принцип суперпозиции Кюри: Когда различные внешние воздействия накладываются друг на друга, образуя единую систему, их диссимметрии складываются. В результате остаются лишь общие элементы симметрии.
 Основные принципы симметрии в кристаллофизике. Принцип Неймана: Физическое свойство кристалла может обладать и более высокой симметрией, чем кристалл, но обязательно должно включать в себя симметрию точечной группы кристалла. Преобразование симметрии, свойственное кристаллу, не может изменить его физического свойства.
Основные принципы симметрии в кристаллофизике. Принцип Неймана: Физическое свойство кристалла может обладать и более высокой симметрией, чем кристалл, но обязательно должно включать в себя симметрию точечной группы кристалла. Преобразование симметрии, свойственное кристаллу, не может изменить его физического свойства.


