Физика твердого тела Лекция 3
1. Группы симметрии конечных фигур (точечные группы), классы симметрии. Группа – совокупность элементов подчиняющаяся определенным правилам (аксиомам). Аксиомы группы: 1. Наличие операции между элементами. a 1*a 2=a 3 2. Наличие единичного элемента. a 1*e=a 1 3. Наличие обратного элемента a 1*a-1=e 4. Ассоциативность операций над элементами группы. (a 1*a 2)*a 3 = a 1*(a 2*a 3)
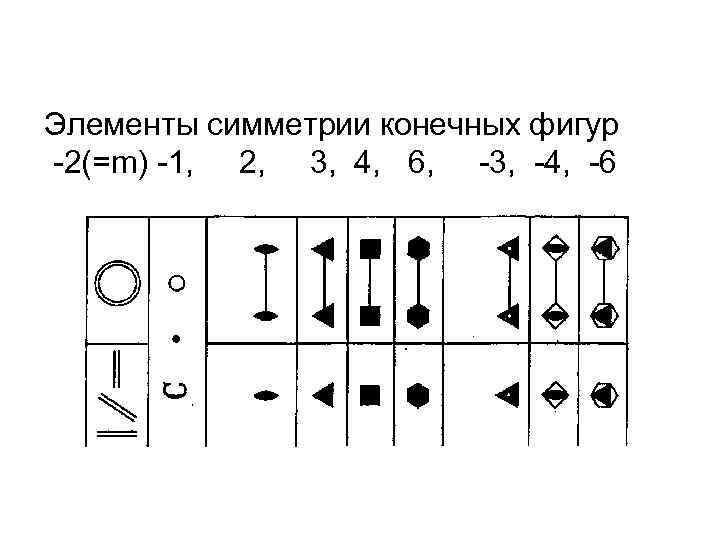Элементы симметрии конечных фигур -2(=m) -1, 2, 3, 4, 6, -3, -4, -6
Примеры точечных групп: {С, 1} • {2, 1} • {2, 1, C, P} • {3, 1, P} Формула симметрии:
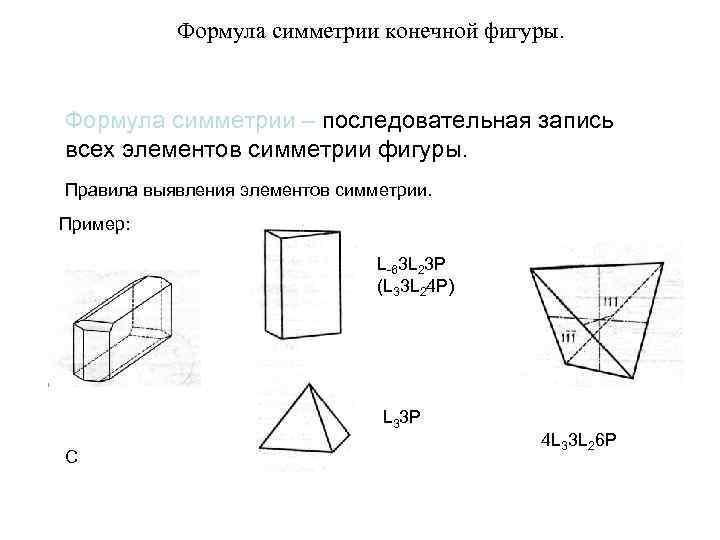Формула симметрии конечной фигуры. Формула симметрии – последовательная запись всех элементов симметрии фигуры. Правила выявления элементов симметрии. Пример: L-63 L 23 P (L 33 L 24 P) L 33 P С 4 L 33 L 26 P
Символика и номенклатура точечных групп симметрии 1. Международные символы Правила составления символа: Все группы делятся на 3 категории: низшая (нет осей высшего порядка) средняя (1 ось высшего порядка) высшая. ( несколько осей высшего порядка) 1. Для высшей категории 1 позиция координатные оси или плоскости. 2 позиция ось 3 -го порядка 3 диагональные элементы 2. Для средней категории различают 3 позиции ( 1, 2, 3) в написании символа группы. 1 - главный элемент, 2. - координатный элемент, 3 –диагональный элемент. 3. Низшая категория: 1. Главный элемент (+ перпендикулярный ). 2. Координатных элемент (// оси)
Символика и номенклатура точечных групп симметрии 1. Международные символы точечных групп Минимальная комбинация элементов симметрии, позволяющая восстановить полный набор элементов. Принятые обозначения: n – ось симметрии -n – инверсионная ось симметрии m – плоскость симметрии nm – ось симметрии n-го порядка и n плоскостей симметрии, проходящих вдоль нее. n/m – ось симметрии n-го порядка и перпендикулярная плоскость. n 2 – ось симметрии n-го порядка и n перпендикулярных осей 2 -го порядка. n/mm - ось симметрии n-го порядка и n плоскости симметрии параллельные и перпендикулярные к ней.
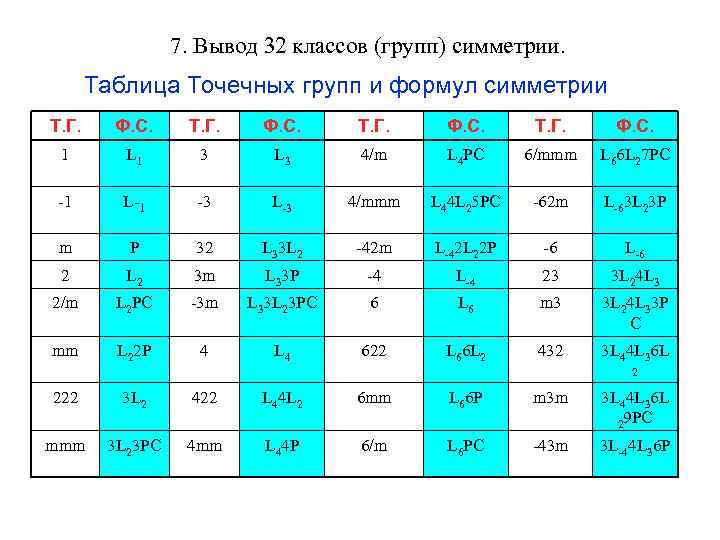7. Вывод 32 классов (групп) симметрии. Таблица Точечных групп и формул симметрии Т. Г. Ф. С. 1 L 1 3 L 3 4/m L 4 PC 6/mmm L 66 L 27 PC -1 L-1 -3 L-3 4/mmm L 44 L 25 PC -62 m L-63 L 23 P m P 32 L 33 L 2 -42 m L-42 L 22 P -6 L-6 2 L 2 3 m L 33 P -4 L-4 23 3 L 24 L 3 2/m L 2 PC -3 m L 33 L 23 PC 6 L 6 m 3 3 L 24 L 33 P C mm L 22 P 4 L 4 622 L 66 L 2 432 3 L 44 L 36 L 2 222 3 L 2 422 L 44 L 2 6 mm L 66 P m 3 m 3 L 44 L 36 L 29 PC mmm 3 L 23 PC 4 mm L 44 P 6/m L 6 PC -43 m 3 L-44 L 36 P
6. Символика и номенклатура точечных групп симметрии 2. Символы Шенфлиса (1891 г) Cn - одна вертикальная полярная ось n-го порядка Cnv - одна вертикальная полярная ось n-го порядка и n-плоскостей, проходящих вдоль нее. Cnh- одна вертикальная полярная ось n-го порядка и плоскость перпендикулярная к ней. Dn- одна вертикальная ось n-го порядка и n осей 2 -го порядка перпендикулярных к ней. Dnh - одна вертикальная полярная ось n-го порядка и плоскость перпендикулярная к ней. Td – оси симметрии тетраэдра и диагональные плоскости. Th - оси симметрии тетраэдра и координатные плоскости. Oh -оси симметрии октаэдра и координатные плоскости. Sn- одна вертикальная зеркально поворотная ось n-го порядка
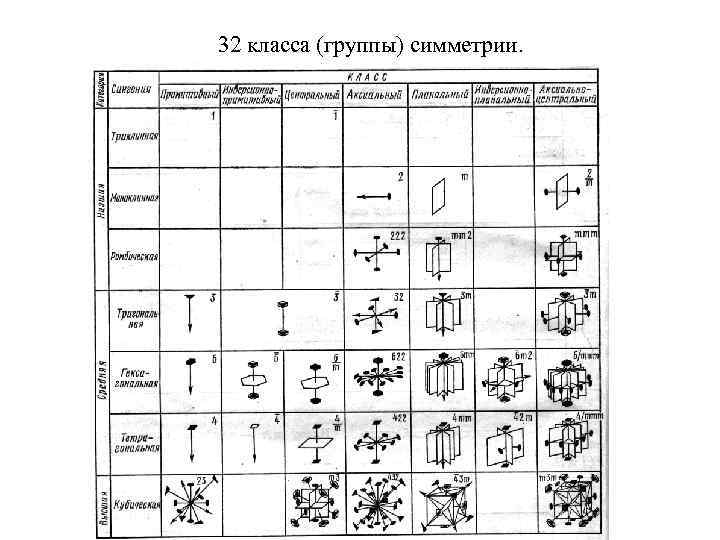32 класса (группы) симметрии.
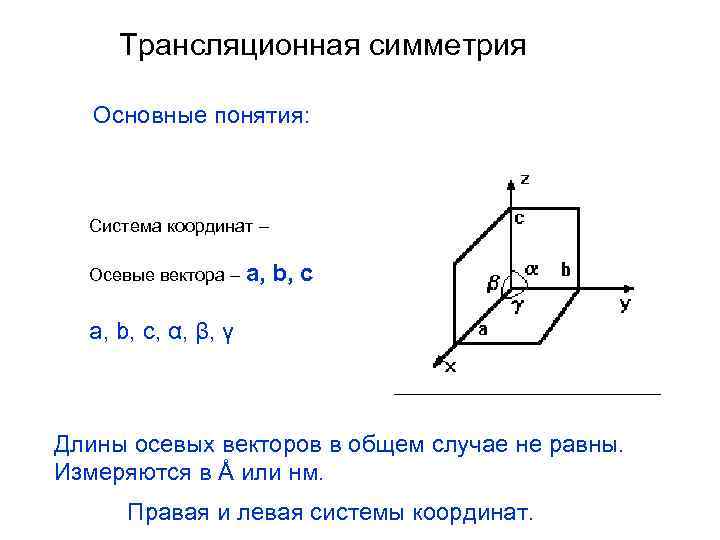Трансляционная симметрия Основные понятия: Система координат – Осевые вектора – a, b, c a, b, c, α, β, γ Длины осевых векторов в общем случае не равны. Измеряются в Å или нм. Правая и левая системы координат.
Трансляционная симметрия Основные понятия: Узел(ы) – точка(и) , выбранная(ые) для обозначения периодичности структуры. Кристаллографическое направление – направление, проходящее по крайней мере через два узла. Трансляция – минимальное расстояние между узлами Плоская сетка – плоскость проходящая через три узла, не лежащих на одной прямой.
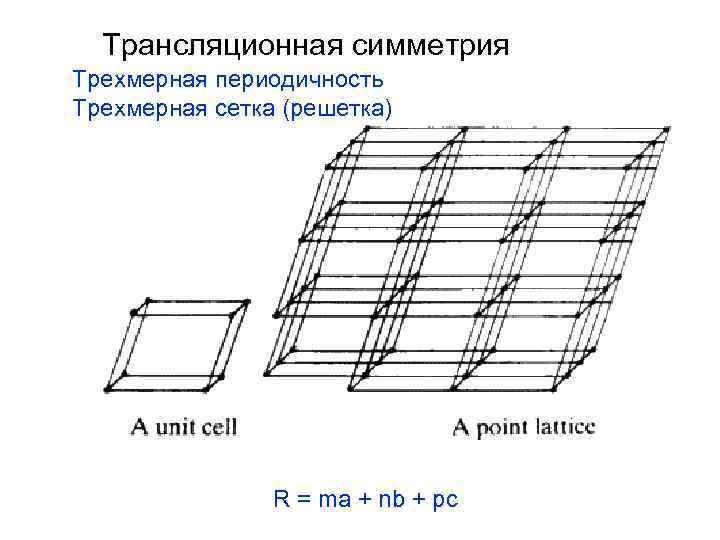Трансляционная симметрия Трехмерная периодичность Трехмерная сетка (решетка) R = ma + nb + pc
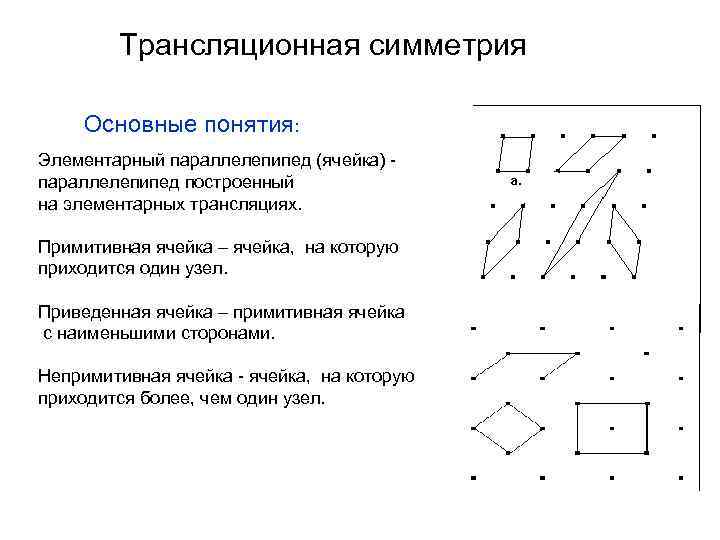Трансляционная симметрия Основные понятия: Элементарный параллелепипед (ячейка) - параллелепипед построенный на элементарных трансляциях. Примитивная ячейка – ячейка, на которую приходится один узел. Приведенная ячейка – примитивная ячейка с наименьшими сторонами. Непримитивная ячейка - ячейка, на которую приходится более, чем один узел.
Трансляционная симметрия Основные понятия: Алгоритм приведения ячейки (преобразования Делоне) Любая ячейка полностью определяется своими периодами и обратной пространственной диагональю: a 0 + b 0 + c 0 + d 0 = 0
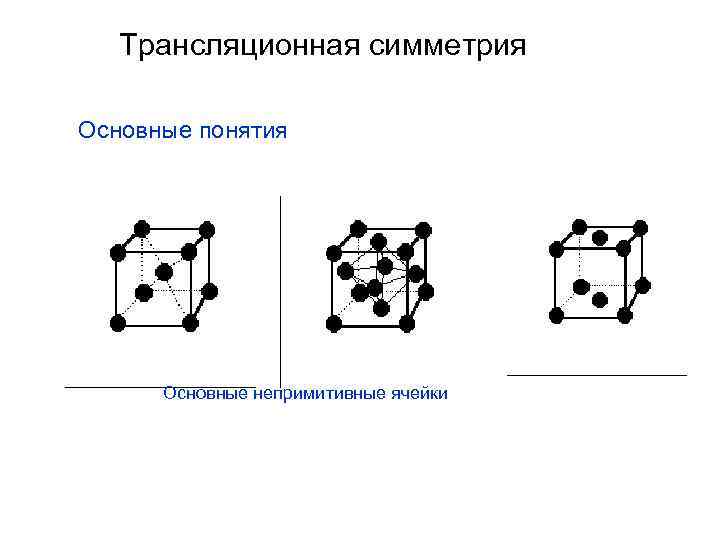Трансляционная симметрия Основные понятия Основные непримитивные ячейки
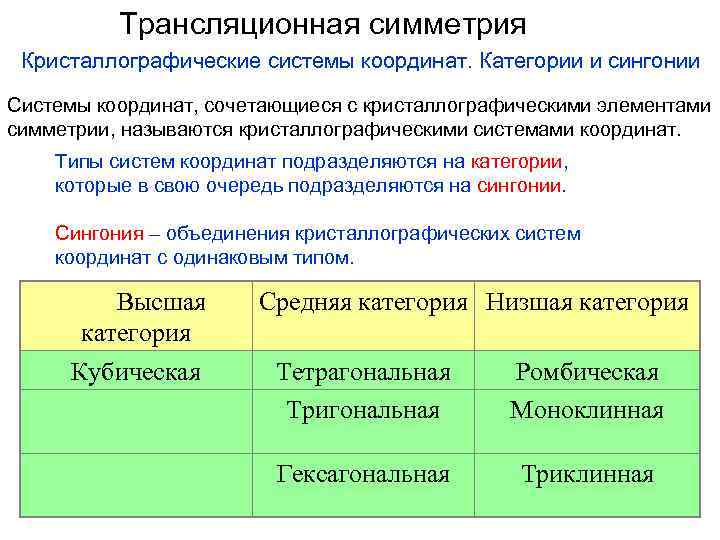Трансляционная симметрия Кристаллографические системы координат. Категории и сингонии Системы координат, сочетающиеся с кристаллографическими элементами симметрии, называются кристаллографическими системами координат. Типы систем координат подразделяются на категории, которые в свою очередь подразделяются на сингонии. Сингония – объединения кристаллографических систем координат с одинаковым типом. Высшая категория Кубическая Средняя категория Низшая категория Тетрагональная Тригональная Ромбическая Моноклинная Гексагональная Триклинная
Кристаллографические системы координат. Ориентация осей и элементов симметрии Кубическая сингония:
Кристаллографические системы координат. Ориентация осей и элементов симметрии Тетрагональная сингония:
Кристаллографические системы координат. Ориентация осей и элементов симметрии Гексагональная сингония:
Кристаллографические системы координат. Ориентация осей и элементов симметрии Тригональная сингония: a = b = c = =
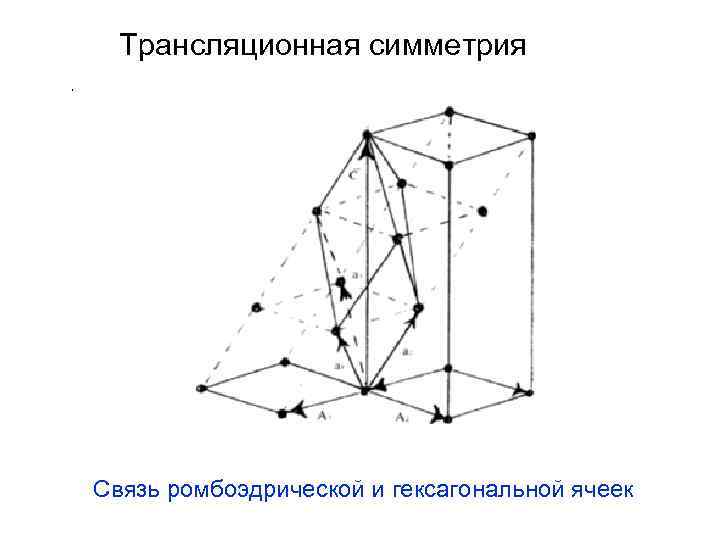Трансляционная симметрия Связь ромбоэдрической и гексагональной ячеек
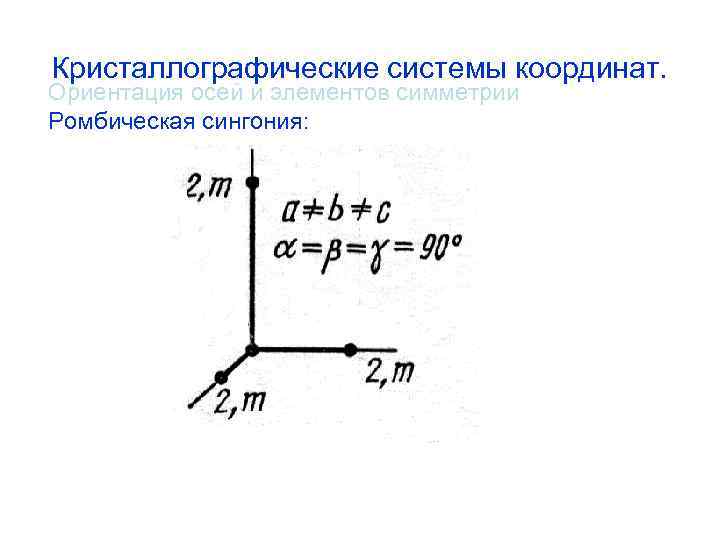Кристаллографические системы координат. Ориентация осей и элементов симметрии Ромбическая сингония:
Кристаллографические системы координат. Ориентация осей и элементов симметрии Моноклинная сингония: c b a
Кристаллографические системы координат. Ориентация осей и элементов симметрии Триклинная сингония: a ≠ b ≠ c ≠ ≠
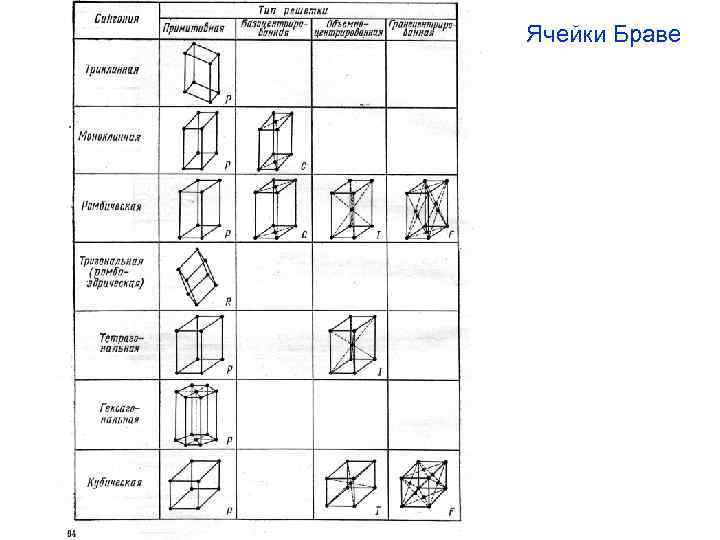
Трансляционная симметрия Ячейки Браве - минимальный набор элементарных ячеек, включающий непримитивные ячейки, и охватывающий все сингонии. Существует 14 типов ячеек. Любую кристаллическую структуру можно представить с помощью одной из 14 решеток Браве. Огюст Браве, 1848 г.
Трансляционная симметрия Правила выбора ячейки Браве. 1. Симметрия выбранного параллелепипеда должна соответствовать симметрии решетки. 2. Число равных ребер и равных углов между ребрами параллелепипеда должно быть наибольшим. 3. При наличии прямых углов между ребрами параллелепипеда их число должно быть максимальным. 4. При соблюдении этих условий объем элементарного параллелепипеда должен быть минимальным.
Ячейки Браве
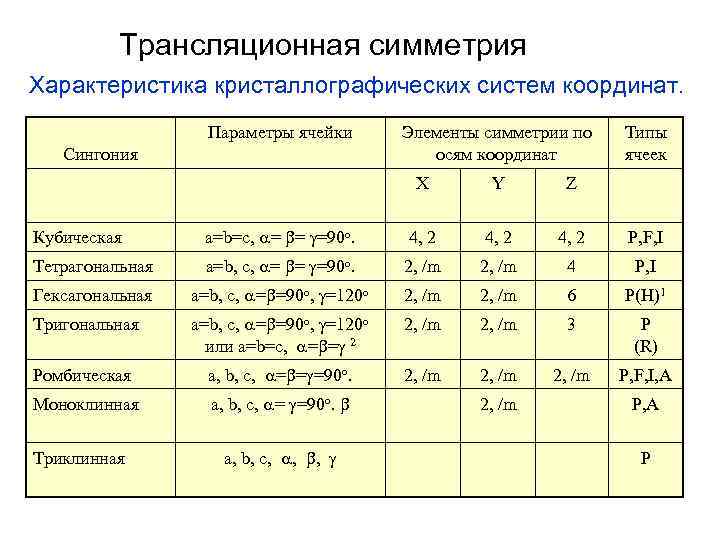Трансляционная симметрия Характеристика кристаллографических систем координат. Параметры ячейки Сингония Элементы симметрии по осям координат X Y Типы ячеек Z Кубическая a=b=c, = = =90 o. 4, 2 P, F, I Тетрагональная a=b, c, = = =90 o. 2, /m 4 P, I Гексагональная a=b, c, = =90 o, =120 o 2, /m 6 P(H)1 Тригональная a=b, c, = =90 o, =120 o или a=b=c, = = 2 2, /m 3 P (R) Ромбическая a, b, c, = = =90 o. 2, /m P, F, I, A Моноклинная a, b, c, = =90 o. Триклинная a, b, c, , , 2, /m P, A P
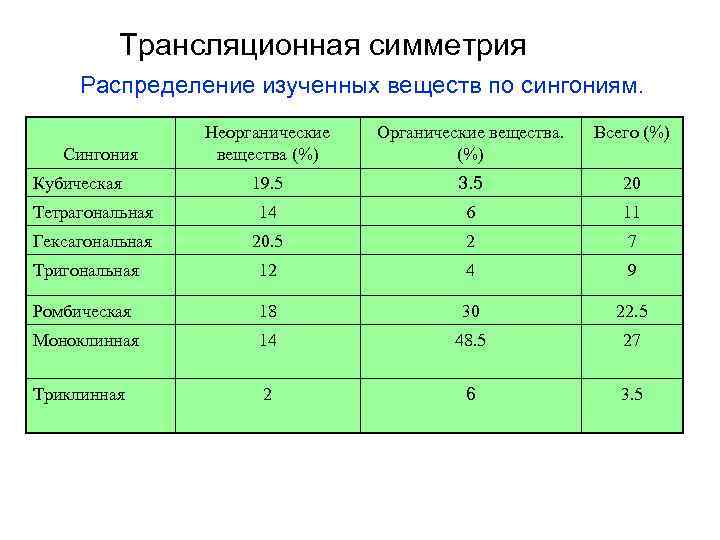Трансляционная симметрия Распределение изученных веществ по сингониям. Неорганические вещества (%) Органические вещества. (%) Всего (%) 19. 5 3. 5 20 Тетрагональная 14 6 11 Гексагональная 20. 5 2 7 Тригональная 12 4 9 Ромбическая 18 30 22. 5 Моноклинная 14 48. 5 27 Триклинная 2 6 3. 5 Сингония Кубическая
Трансляционная симметрия Решеточная кристаллография Свойства кристаллографических плоскостей. 1) каждая узловая плоскость содержит бесконечное количество узлов; 2) через любой узел решетки не лежащий в плоскости может быть проведена параллельная узловая плоскость; 3) через любой узел решетки проходит бесконечное количество узловых плоскостей.
Трансляционная симметрия Решеточная кристаллография Уравнение узловой плоскости: hx + ky + lz = p (h, k, l – взаимнопростые целые числа) x, y, z – координаты в относительных долях ячейки. hkl – индексы Миллера Межплоскостное расстояние: d(hkl)
Трансляционная симметрия Теоремы решеточной кристаллографии: Теорема 1. Последовательные узловые плоскости семейства (hkl) рассекают стороны элементарной ячейки a, b, c, соответственно, на h, k, l частей, телесную диагональ на (h+k+l) частей, а диагонали граней на (k+l), (h+l) и (h+k) частей.
Трансляционная симметрия Теоремы решеточной кристаллографии: Теорема 2. Если N(hkl) - есть единичный вектор перпендикулярный к плоскости hkl, справедливо соотношение:
Трансляционная симметрия Теоремы решеточной кристаллографии: следствия 1. Кубическая сингония: 2. Тетрагональная сингония: 3. Гексагональная сингония: 4. Ромбческая сингония:
Трансляционная симметрия Теоремы решеточной кристаллографии: следствия Общий случай:
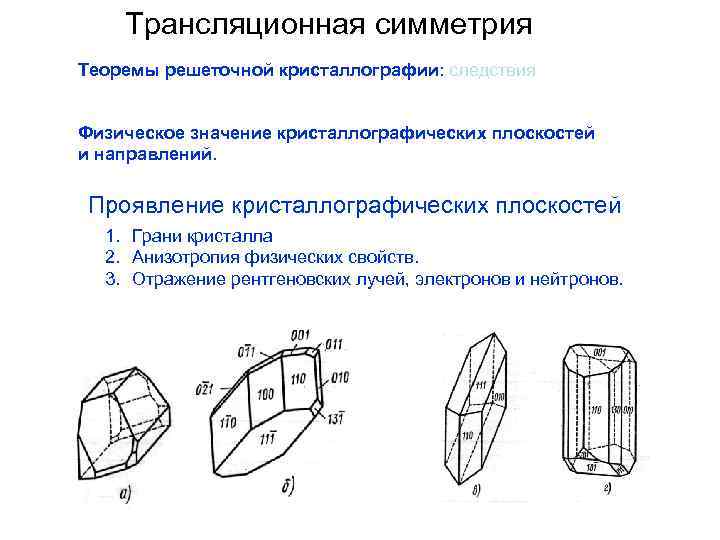Трансляционная симметрия Теоремы решеточной кристаллографии: следствия Физическое значение кристаллографических плоскостей и направлений. Проявление кристаллографических плоскостей 1. Грани кристалла 2. Анизотропия физических свойств. 3. Отражение рентгеновских лучей, электронов и нейтронов.
Трансляционная симметрия Индицирование (определение символов) граней кристаллов.
Трансляционная симметрия Понятие простой формы. Простая форма - совокупность граней кристалла, связанных элементами симметрии. Грани одной простой формы обозначаются однотипными индексами. Полная совокупность граней одной простой формы может быть получена путем размножения любой из этих граней с помощью элементов симметрии кристалла.
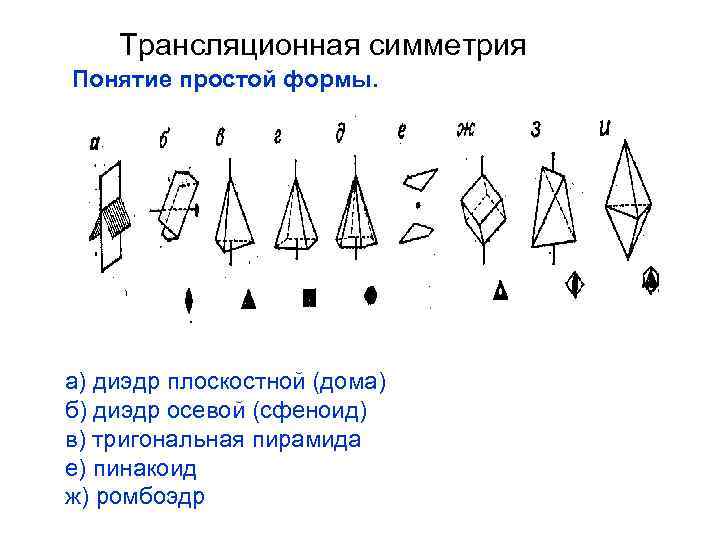Трансляционная симметрия Понятие простой формы. а) диэдр плоскостной (дома) б) диэдр осевой (сфеноид) в) тригональная пирамида е) пинакоид ж) ромбоэдр
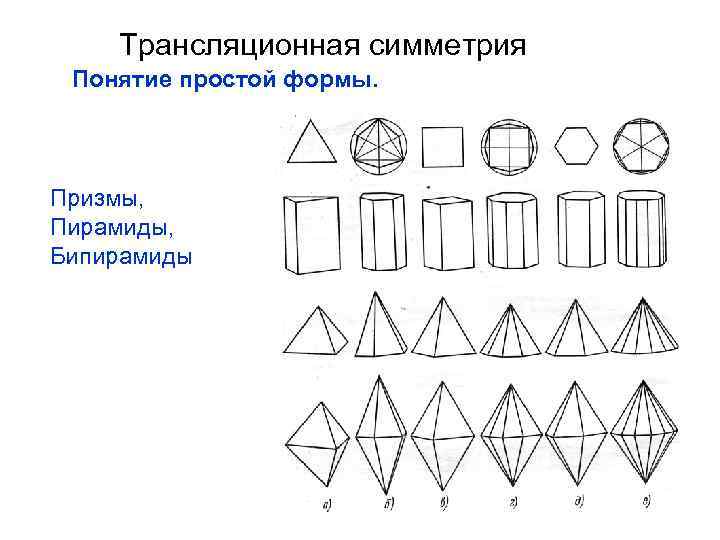Трансляционная симметрия Понятие простой формы. Призмы, Пирамиды, Бипирамиды
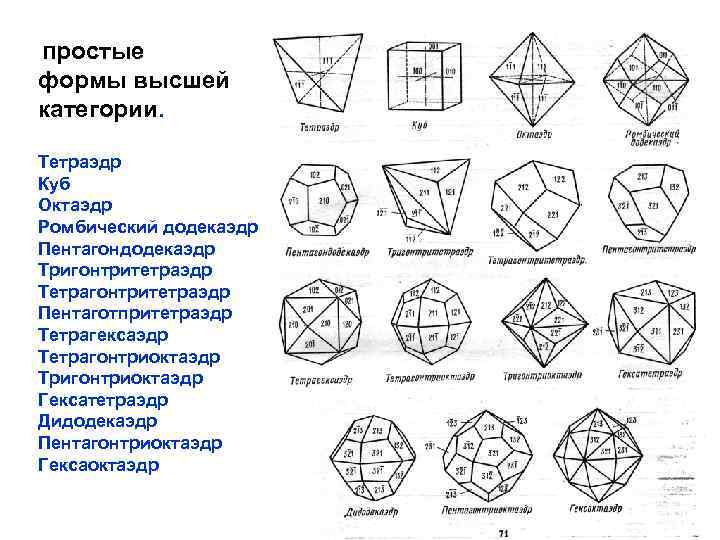Простые формы высшей категории. Тетраэдр Куб Октаэдр Ромбический додекаэдр Пентагондодекаэдр Тригонтритетраэдр Тетрагонтритетраэдр Пентаготпритетраэдр Тетрагексаэдр Тетрагонтриоктаэдр Тригонтриоктаэдр Гексатетраэдр Дидодекаэдр Пентагонтриоктаэдр Гексаоктаэдр
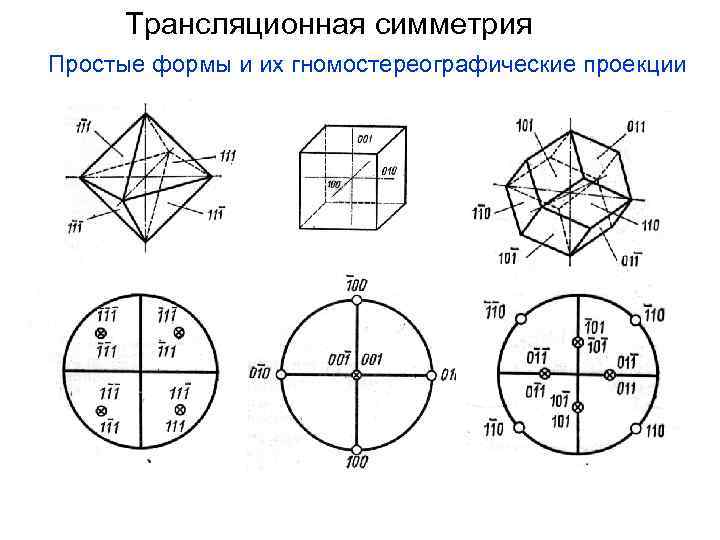Трансляционная симметрия Простые формы и их гномостереографические проекции
Трансляционная симметрия Обратная решетка 1. Упрощение при расчете скалярных произведений: (r. H) = r. H cos(φ) Для ортогональной системы: (r. H) = rx. Hx + ry. Hy + rz. Hz 2. Упрощенный геометрический способ описания дифракции на кристаллической структуре. 3. Описание пространства волновых векторов электронных волн, Колебательных волн.
Трансляционная симметрия Обратная решетка 1. 2. (a*·b) = (a*·c) = 0 (b*·a) = (b*·c) = 0 (c*·a) = (c*·b) = 0 (a·a*) = M (b·b*) = M (c·c*) = M (М = 1)
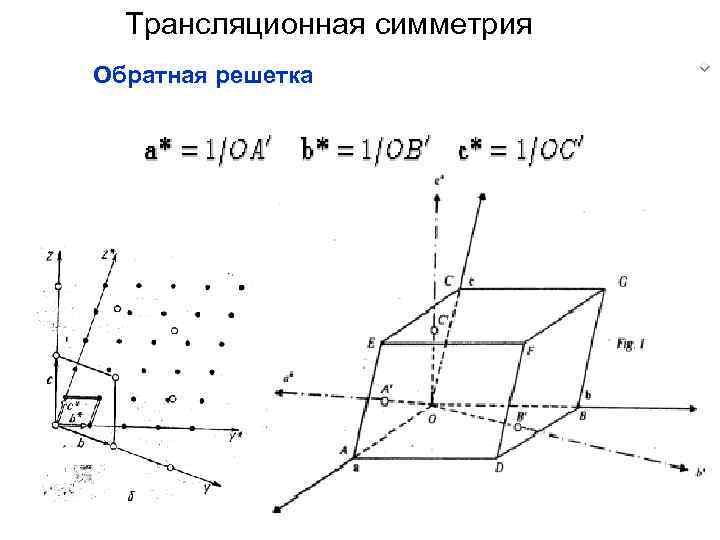Трансляционная симметрия Обратная решетка
Трансляционная симметрия Обратная решетка Скалярное произведение:
Трансляционная симметрия Обратная решетка Геометрический смысл соотношений: (a*·b) = (a*·c) = 0 (b*·a) = (b*·c) = 0 (c*·a) = (c*·b) = 0 (a·a*) = M (b·b*) = M (c·c*) = M (М = 1) a* = M/d 100 b* = M/d 010 c* = M/d 001 Hhkl = ha* + kb* + lc* = M Nhkl /dhkl
Трансляционная симметрия Обратная решетка Геометрический смысл соотношений: (Hhkl ·Hhkl) = M 2/(dhkl)2 1/(dhkl)2 = h 2(a*)2 + k 2(b*)2 + l 2(c*)2 + +2 hka*b*cos(α*) + 2 hla*c*cos(β*) + 2 klc*b*cos(γ*)
Трансляционная симметрия Обратная решетка Полезные соотношения:
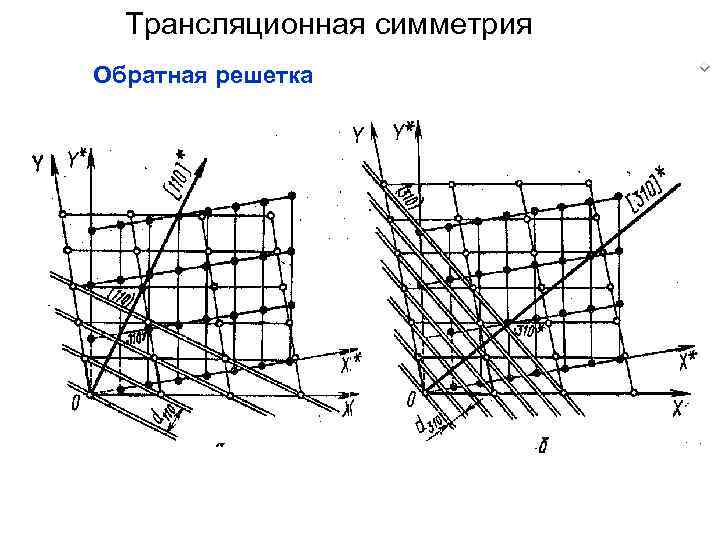Трансляционная симметрия Обратная решетка