Физика твердого тела Курс лекций 8 1 Статистика

Физика твердого тела Курс лекций (8) 1. Статистика Ферми-Дирака для вырожденного и невырожденного электронного газа.

Закон распределения Ферми-Дирака. 1. Для описания свойств идеального газа вполне корректно применяют закон распределения Максвелла-Больцмана. Е –полная энергия μ – химических потенциал (внутренняя энергия) Для электронов классическая статистика не применима: а) Концентрация электронов в металле в 104 раз больше, чем концентрация атомов в газе при нормальных условиях. б) Заполнение вакантных электронных состояний происходит при действии принципа Паули. Электрон (фермион) не может перейти в состояние, которое занято) В применении к электронам квантовая статистика требует включения таких положений, как: • неразличимость электронов; • единственность квантового состояния электрона.

Поскольку в данном состоянии может находиться только один электрон, отсюда следует, что при большом числе электронов окажутся занятыми состояния с большими квантовыми числами и , соответственно, с большей энергией. В этом состоит существенное отличие статистики электронов в твердом теле (статистики Ферми-Дирака) от классической статистики, для которой любое число частиц может иметь одинаковые энергию и импульс. Как изменится состояние электронов при повышении температуры? Вследствие увеличения кинетической энергии электронного газа происходит процесс перехода электронов на более высокие энергетические уровни, которые были вакантными при абсолютном нуле. Освобождается часть уровней, занятых при абсолютном нуле. Устанавливается термодинамического равновесие, описываемое распределением Ферми-Дирака, которое определяет: Вероятность того, что состояние с энергией Е занято, когда система частиц находится в тепловом равновесии при температуре Т.

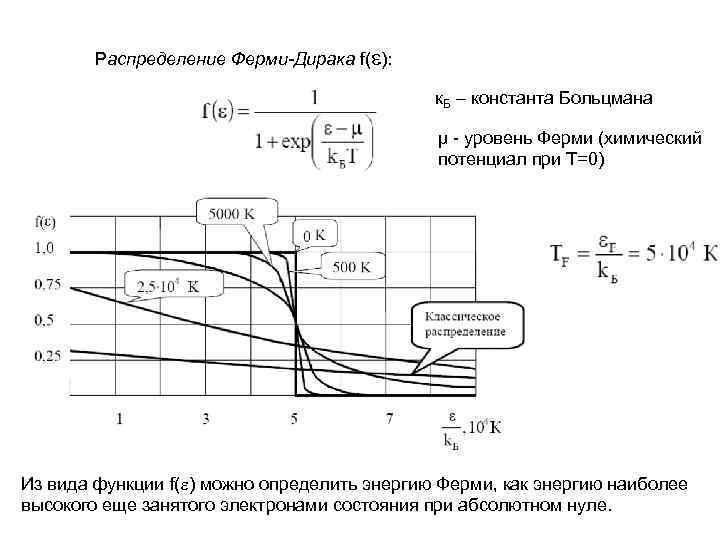Распределение Ферми-Дирака f( ): к. Б – константа Больцмана μ - уровень Ферми (химический потенциал при Т=0) Из вида функции f( ) можно определить энергию Ферми, как энергию наиболее высокого еще занятого электронами состояния при абсолютном нуле.

При соотношение соответствует классической функции распределения Больцмана. Плотность электронных состояний. Вырождение электронного газа в металлах Распределение электронов по энергиям подчиняется статистике Ферми-Дирака. Кроме функции распределения для анализа электронной системы используют функцию плотности электронных состояний D(Е). В силу того, что число атомов и размеры кристалла велики, разница между «соседними» значениями волновых векторов Δk 0 и следует говорить не о дискретном, а о квазинепрерывном спектре электронных состояний. Определим плотность электронных состояний (ПЭС) D(Е) таким образом, чтобы в интервал энергий d. Е попадало d. N электронных состояний:

Определим плотность электронных состояний (ПЭС) D( ) таким образом, чтобы в интервал энергий d попадало d. N электронных состояний: Аналитический вид функции плотности электронных состояний D(E) в общем случае неизвестен. В координатах пространства волновых векторов можно записать уравнение сферы: или Изоэнергетические поверхности свободных электронов в пространстве волновых векторов Значению энергии Е соответствует сфера радиуса k с центром в начале координат, значению энергии Е+d. E - сфера радиуса k+dk.

Сферический слой в пространстве волновых векторов с толщиной dk имеет объем: В него попадают энергетические состояния в интервале от Е до Е+d. E Если - объем одного состояния, то можно рассчитать количество состояний в сферическом слое. множитель « 2» учитывает спиновое вырождение электронов по энергиям: в одном состоянии сосуществуют 2 электрона с антипараллельными спинами. Тогда можно записать, используя:

где V – объем кристалла. Получаем выражение для плотности электронных состояний (ПЭС) свободных электронов: Плотность состояний свободных электронов Плотность состояний является монотонной возрастающей функцией энергии. Чем больше величина энергии, тем большее число электронных состояний. С увеличением энергии возрастает кратность вырождения энергетических состояний. Т=0

Рассчитаем полное число электронов в системе при конечной температуре Т: Где f(e) – функция Ферми-Дирака которая представляет собой вероятность того, что состояние с энергией Е занято. Рассмотрим электронный газ в твердом теле, находящемся при Т = 0. При этом Ее

Поэтому для числа электронов можно записать упрощенное выражение: Тогда поставляя D(E), получим: Откуда следует: Рассчитаем среднюю энергию электронов при Т = 0: Подставляя n, получаем:

Средняя энергия электронов при Т = 0 отлична от нуля (!) и для различных кристаллов составляет величину 4 -6 э. В. Свободный электронный газ при Т = 0 является полностью вырожденным по своим квантовым состояниям. То есть при Т = 0 любой электрон может занять любое из указанных энергетических состояний. Все электронные состояния с энергиями Е

Более удобно использовать такой параметр, как температура Ферми, которая определяется так: E=k. T Отсюда следует, что температура Ферми, или температура вырождения электронного газа, зависит только от концентрации электронов в твердом теле. Рассмотрим сейчас случай низких температур, когда выполняется неравенство: Имеется два случая: 1. а) Если: Вероятность заполнения: б)при приближении к уровню Ферми: Выражение находится в пределах: Вероятность лежит в пределах:

2. Тогда член Для вероятности имеем При Функция распределения по электронным состояниям (Ферми-Дирака) Функция плотности электронных состояний

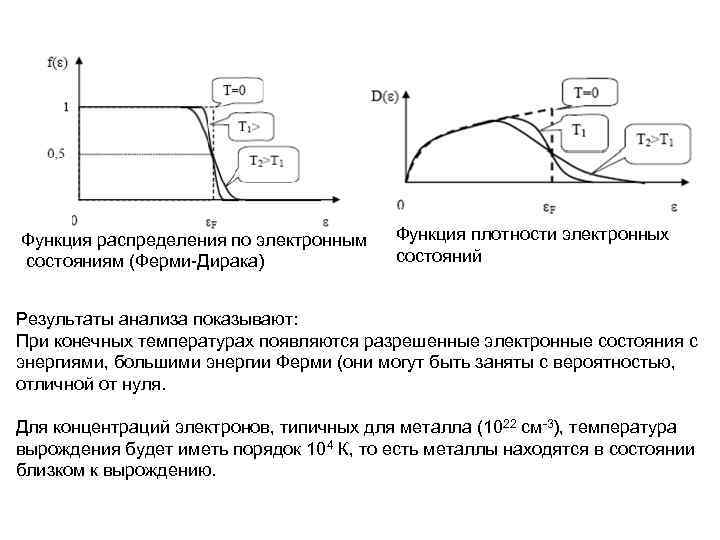Функция распределения по электронным состояниям (Ферми-Дирака) Функция плотности электронных состояний Результаты анализа показывают: При конечных температурах появляются разрешенные электронные состояния с энергиями, большими энергии Ферми (они могут быть заняты с вероятностью, отличной от нуля. Для концентраций электронов, типичных для металла (1022 см-3), температура вырождения будет иметь порядок 104 К, то есть металлы находятся в состоянии близком к вырождению.

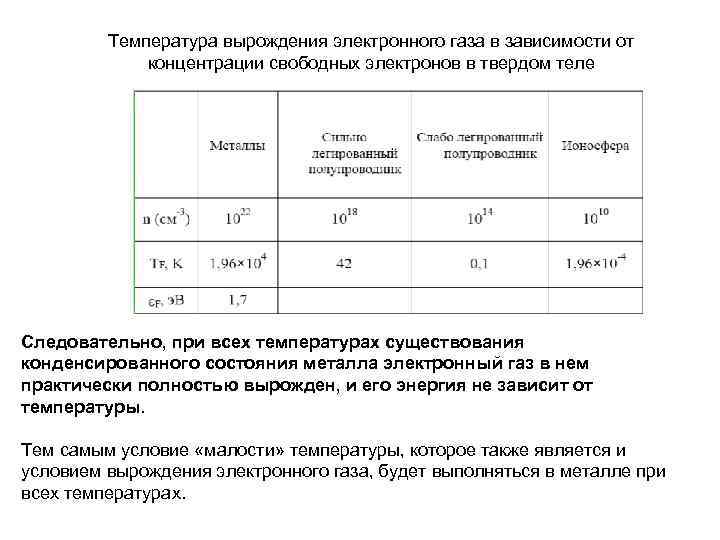Температура вырождения электронного газа в зависимости от концентрации свободных электронов в твердом теле Следовательно, при всех температурах существования конденсированного состояния металла электронный газ в нем практически полностью вырожден, и его энергия не зависит от температуры. Тем самым условие «малости» температуры, которое также является и условием вырождения электронного газа, будет выполняться в металле при всех температурах.