Физика твердого тела Курс лекций 13 1 Статистика

Физика твердого тела Курс лекций (13) 1. Статистика электронов в полупроводниках 2. Собственная проводимость.

Полупроводниками являются: элементы IVa – подгруппы Периодической системы: алмаз, кремний, германий, серое олово; AIVBIV (карбид кремния Si. C) многие оксиды, например Fe 2 O 3, Cu 2 O; соединения AIIIBV (Ga. As, In. Sb, …), соединения AIIBVI (Cd. S, Zn. S, …), селен Se и другие.

Полупроводниковые эффекты применяются в большом разнообразии приборов и устройств: · Полупроводниковые термоэлектрогенераторы; · Полупроводниковые диоды для выпрямления переменного тока и детектирования модулированных колебаний; · Туннельные диоды для генерации сверхвысокочастотных электромагнитных волн; · Свето и фотодиоды, фотоэлементы, солнечные батареи; · Термисторы и тензорезисторы (сопротивление зависит от температуры или механического давления); · Варикапы (конденсаторы с изменяемой электрическим полем емкостью); · Биполярные и полевые транзисторы, микросхемы; · Запоминающие устройства (оперативная память ЭВМ); · Приборы с зарядовой связью (для создания миниатюрных видеокамер); · Высокотемпературные полупроводниковые нагревательные элементы.

Совершенные кристаллы полупроводников при абсолютном нуле являются диэлектриками. Характерные для полупроводников свойства проявляются: -при конечных температурах, -при наличии примесей, -при отклонениях состава вещества от стехиометрии. Проводимость полупроводников по сравнению с типичными диэлектриками и металлами имеет промежуточное значение · диэлектрики - ~ 10 -16 Ом-1×м-1; · полупроводники - ~ (10 -4 … 105) Ом-1×м-1 ; · металлы - ~ (106 … 108) Ом-1×м-1. Концентрация свободных электронов в различных веществах.

Эффект собственной проводимости и ширина запрещенной зоны Беспримесные кристаллы полупроводников и многие диэлектрики обнаруживают проводимость, возрастающую с ростом температуры. Это объясняется термической активацией электронов: их перебросом из зоны с занятыми состояниями (валентной зоны) в зону, первоначально свободную от электронов, которую называют зоной проводимости Вероятность переброса резко возрастает, когда выполняется неравенство: Eg – ширина запрещенной зоны Чем меньше ширина запрещенной зоны, тем больше при данной температуре электронов переходит из валентной зоны в зону проводимости.

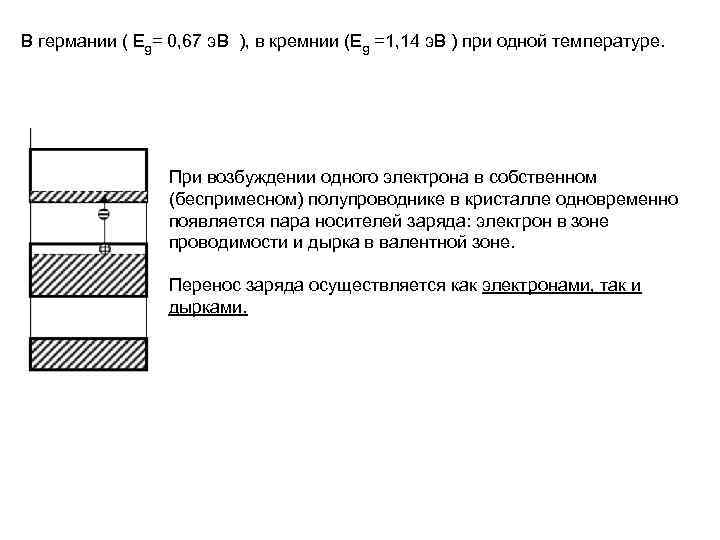В германии ( Eg= 0, 67 э. В ), в кремнии (Eg =1, 14 э. В ) при одной температуре. При возбуждении одного электрона в собственном (беспримесном) полупроводнике в кристалле одновременно появляется пара носителей заряда: электрон в зоне проводимости и дырка в валентной зоне. Перенос заряда осуществляется как электронами, так и дырками.

Переход электронов внутри валентной зоны Переход электронов внутри зоны валентных уровней из одного состояния в другое носит «эстафетный» характер: Электрон, переходя на свободный энергетический уровень, остается на нем, а освобожденный уровень заполняется другим электроном, который освобождает свой уровень для последующего электрона. При таком способе перехода освобождающиеся состояния ведут себя подобно частицам с положительным электрическим зарядом, которые перемещаются в направлении, противоположном движению электронов при действии электрического поля. В упрощенном представлении такие квазичастицы, называемые дырками (hole), рассматриваются как частицы с массами, равными массе электрона.

Электроны, попавшие в зону проводимости, могут снова стать валентными - перейти в валентную зону, Происходит акт аннигиляции (рекомбинации) электрона и дырки. При данной температуре образуются и новые электроннодырочные пары. Устанавливается динамическое равновесное состояние: «среднее число электронов проводимости равно среднему числу дырок» .

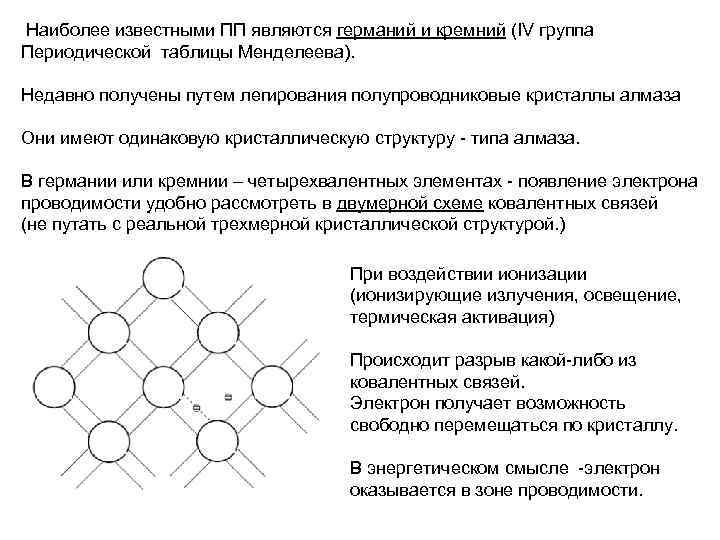Наиболее известными ПП являются германий и кремний (IV группа Периодической таблицы Менделеева). Недавно получены путем легирования полупроводниковые кристаллы алмаза Они имеют одинаковую кристаллическую структуру - типа алмаза. В германии или кремнии – четырехвалентных элементах - появление электрона проводимости удобно рассмотреть в двумерной схеме ковалентных связей (не путать с реальной трехмерной кристаллической структурой. ) При воздействии ионизации (ионизирующие излучения, освещение, термическая активация) Происходит разрыв какой-либо из ковалентных связей. Электрон получает возможность свободно перемещаться по кристаллу. В энергетическом смысле -электрон оказывается в зоне проводимости.

Невырожденный электронный газ в полупроводниках Состояние электронного газа в полупроводниках (ПП) отличается от металла. В ПП любых температурах реализуется ситуация невырожденного электронного газа. Условие выполняется, когда концентрация электронов в зоне проводимости мала. Это реализуется в ПП практически во всем возможном диапазоне концентраций носителей – -от минимальной в «чистых» (1014 см-3) материалах при конечных температурах, -до максимально возможной 1018 см-3 в сильно легированном ПП.

Действительно, в этом случае температура вырождения (Температура Ферми) мала, и при нормальных условиях (температурах) и стандартных концентрациях электронов (дырок) ~1014 см-3 Возникает ситуация невырожденного электронного газа Исключение - существование вырождения электронного газа в полупроводнике – при сильном легировании полупроводника и при низких температурах. В этом случае существуют электроны, энергия которых должна быть значительно больше уровня Ферми. Условие невырожденного электронного газа в полупроводнике при конечных температурах может быть записано так: Подстановка условия в функцию распределения Ферми – Дирака приводит к тому, что выполняется:

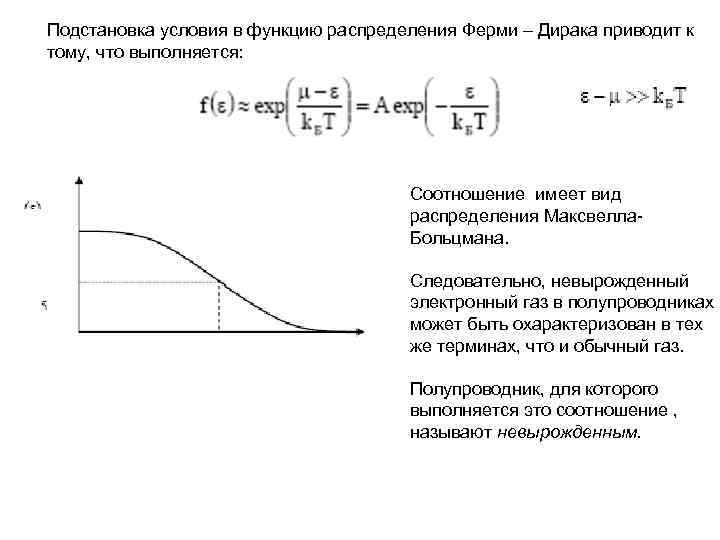Подстановка условия в функцию распределения Ферми – Дирака приводит к тому, что выполняется: Соотношение имеет вид распределения Максвелла. Больцмана. Следовательно, невырожденный электронный газ в полупроводниках может быть охарактеризован в тех же терминах, что и обычный газ. Полупроводник, для которого выполняется это соотношение , называют невырожденным.

Концентрация электронов (дырок) в зоне проводимости (валентной зоне). Закон действующих масс Рассчитаем концентрацию электронов в зоне проводимости ПП при конечных температурах. Воспользуемся представлением электронного газа в модели сильной связи, справедливым в окрестности центра зоны Бриллюэна. Отсчет энергии осуществляется от дна зоны проводимости Ес (индекс “с” – от англ. “conductivity” - проводимость): m – эффективная масса электронов в твердом теле. Преобразуем и Получаем:

Ранее для плотности электронных состояний было получено: В данном случае формула преобразуется в: Важное отличие от плотности электронных состояний в металлах состоит в том, что используется эффективная масса электронов.

Принимая, что полупроводник – невырожденного типа, и для него справедливо распределение, для числа электронов на единицу объема (концентрации) электронов в зоне проводимости получим: -эффективная плотность состояний электронов в зоне проводимости, Интеграл Ферми-Дирака. Значение : Получаем:

Концентрация электронов в зоне проводимости невырожденного полупроводника в зависимости от температуры: Из полученного выражения можно определить положение уровня Ферми при данной температуре и концентрации электронов: Вывод из формулы : чем больше концентрация электронов, тем ближе уровень Ферми к дну зоны проводимости. (оставаясь в зоне проводимости),

Концентрация «дырок» : При термическом (или ином) переходе одного электрона в зону проводимости одновременно появляется пара носителей заряда: электрон (в зоне проводимости) и «дырка» (в валентной зоне) Концентрация дырок в валентной зоне может быть подсчитана по аналогии. Отсчет энергии для дырок в валентной зоне должен осуществляться от потолка валентной зоны Еv. Для “свободных” дырок, действующий на границе зоны Бриллюэна – вблизи максимума энергии в разрешенной зоне (потолка валентной зоны), то можно записать: mh – эффективная масса дырки в кристалле, общем случае, существенно отличающаяся как от массы свободного электрона

Функция плотности состояний дырок в валентной зоне вблизи ее потолка будет иметь вид: Вероятность обнаружить дырку с данной энергией при определенной температуре может быть также определена с помощью функции типа распределения Ферми-Дирака, Однако в данном случае нужно найти вероятность отсутствия электрона: Аналогично невырожденному электронному газу существует газ невырожденных дырок, поэтому соотношение приобретает вид:

Для концентрации дырок nр в валентной зоне имеем: Положение уровня Ферми аналогично вычисляется при данной температуре и концентрации дырок по уравнению : Для собственного полупроводника (без примесей) выполняется условие: Перемножая выражения для концентраций получим, что произведение не зависит от уровня Ферми: -ширина запрещенной зоны.

Полученное соотношение - закон действующих масс служит для определения концентрацию электронов (дырок) в собственном (без примесей) невырожденном ПП при конечных температурах: Положение уровня Ферми в собственном полупроводнике из соотношения: Откуда где положение центра запрещенной зоны

Уровень Ферми в точности совпадает с положением центра запрещенной зоны при абсолютном нуле и приближенно – при mh » me для конечных температур. Эта зависимость может быть аппроксимирована соотношением: Для большинства полупроводников ширина запрещенной зоны слабо зависит от температуры. Качественное объяснение этой зависимости можно дать, если учесть, что, благодаря ангармонизму колебаний решетки, помимо теплового расширения, возникает взаимодействие электронов с колебаниями решетки, благодаря чему валентные электроны приобретают дополнительную энергию, что и соответствует уменьшению ширины запрещенной зоны.

Собственная проводимость полупроводников Как и в металлах, удельная электронная электропроводность в полупроводнике имеет вид: - подвижность электронов время между последовательными актами рассеяния дырки (время релаксации), р и mh – концентрация и эффективная масса дырок. Проводимость собственного полупроводника определяется суммой вкладов

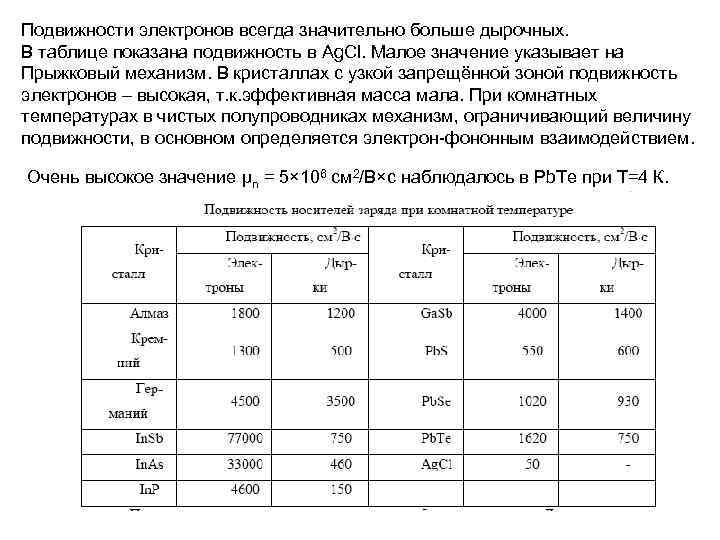Подвижности электронов всегда значительно больше дырочных. В таблице показана подвижность в Ag. Cl. Малое значение указывает на Прыжковый механизм. В кристаллах с узкой запрещённой зоной подвижность электронов – высокая, т. к. эффективная масса мала. При комнатных температурах в чистых полупроводниках механизм, ограничивающий величину подвижности, в основном определяется электрон-фононным взаимодействием. Очень высокое значение μn = 5× 106 см 2/В×с наблюдалось в Pb. Te при Т=4 К.