Физика твердого тела Глава 1 Элементы квантовой статистики

Физика твердого тела Глава 1. Элементы квантовой статистики Выполнил: Максимов Михаил гр. АВ-10 -2

1. Физика твердого тела – один из важнейших разделов науки, лежит в основе материаловедения, производства полупроводников, сегнетоэлектриков, магнитных материалов, искусственных драгоценных камней, оптических кристаллов и т. д. Предмет ФТТ – изучение состава твердых тел, их атомно-электронной структуры и физических свойств.

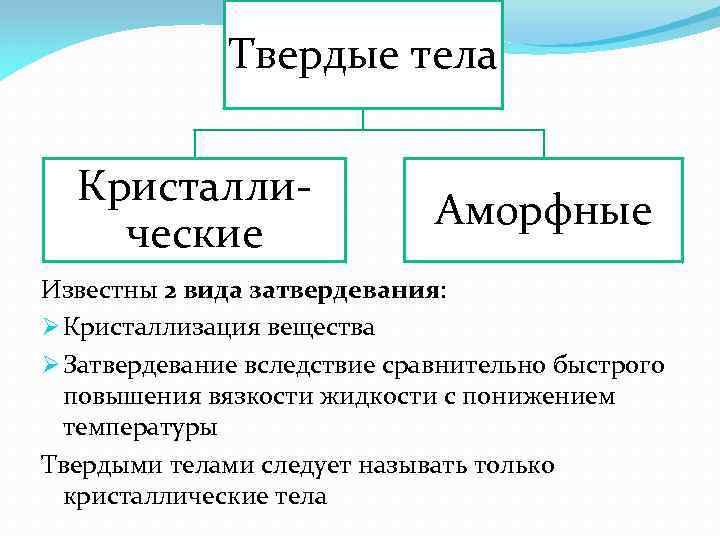Твердые тела Кристаллические Аморфные Известны 2 вида затвердевания: Ø Кристаллизация вещества Ø Затвердевание вследствие сравнительно быстрого повышения вязкости жидкости с понижением температуры Твердыми телами следует называть только кристаллические тела

Твердое тело, обладающее пространственной периодичностью в расположении равновесных положений, составляющих их частиц (атомов, ионов), называется кристаллическим. Аморфные тела не обладают четко выраженными свойствами кристаллов.

Квантовая статистика - раздел статистической физики, исследующий системы множества частиц, подчиняющихся законам квантовой механики. Квантовая статистика строится на принципе неразличимости тождественных частиц, согласно которому невозможно экспериментально различить тождественные частицы.

По виду ψ все элементарные частицы и построенные из них делятся на 2 класса: Ø Частицы с полуцелым спином (e, p, n) ħ/2, 3/2ħ – фермионы ( «индивидуалисты» ). Подчиняются принципу Паули. Ø Частицы с нулевым или целочисленным спином 0, ħ – бозоны ( «коллективисты» ). Принцип Паули не накладывает ограничений на число частиц, находящихся в некотором квантовом состоянии.

2. Специфика микрочастиц определяется вероятностью попадания в одно и то же состояние «заселения» N – число одинаковых частиц G – число допустимых энергетических состояний, в которых могут находится эти N частиц • Если N/G << 1, то частицы будут «встречаться» редко. Коллектив называется невырожденным. • Если N/G ≈ 1, то вопрос о том, как «заселены» состояния актуален. Коллектив называется вырожденным.

Система состояний частиц называется вырожденной, если ее свойства, описываемые квантовыми закономерностями, отличаются от свойств обычных систем, подчиняющихся классическим законам.

Критерий невырожденности: Для идеального газа: - число состояний частиц, энергия которых лежит в интервале от W до W+∆W. При N/G << 1 газ невырожден, т. е. - условие невырожденности

4. Классическая статистика – статистика, изучающая свойства невырожденного коллектива. 5. Квантовая статистика – статистика, изучающая свойства вырожденного коллектива. Существуют 2 статистики: Ø Статистика Ферми-Дирака для фермионов Ø Статистика Бозе-Эйнштейна для бозонов

Статистическое распределение Ферми-Дирака Объект описания – электронный газ в металле Функция распределения: где μ – энергия Ферми

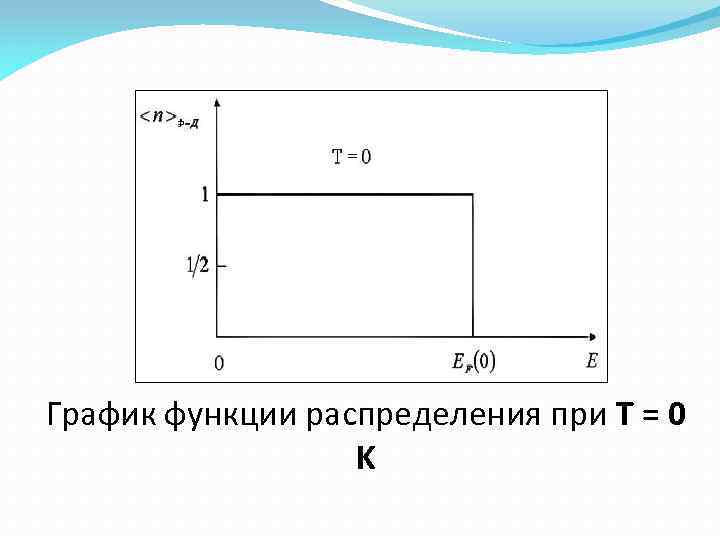График функции распределения при T = 0 K

Средняя энергия электронов при Т=0: - температура вырождения Для электронов в металле ТФ ~ 104 К Литий: ЕФ = 4, 72 э. В, VФ = 1, 3*106 м/с = 2, 8 э. В, ТФ = 5, 5*104 К

При Т ≠ 0 функция распределения Ферми-Дирака имеет вид сплошной линии При E-μ >> k. T ( «хвост» Ф. -Д. ) – распределение Максвелла-Больцмана

Распределение Бозе-Эйнштейна Применяется для бозонов (напр. фотоны). С помощью данного распределения можно определить теплоемкость твердых тел, тепловое расширение твердых тел.

Глава 2. Зонная теория твердых тел Рассмотрим кристалл 11 Na: 1 s 22 p 63 s 1 s-уровни (l=0) - невырожденные; p-уровни (l=1) – 3 -х кратно вырожденные: каждому из них соответствует 3 состояния, которые различаются магнитным квантовым числом ml : ml = -1, 0, +1. d-уровни (l=2) – пятикратно вырожденные ml = -2, -1, 0 , +1, +2. При помещении свободного атома в сильное внешнее поле вырождение уровней снимается.

Образование зон энергетического спектра в кристалле вытекает из соотношения неопределенностей: ∆E∆t ≥ ħ, ∆t – время жизни электрона в возбужденном состоянии, ~10 -8 с. Каждому энергетическому уровню изолированного атома в кристалле соответствует зона разрешенных энергий: уровню 1 s – зона 1 s уровню 1 p – зона 1 p и т. д. Зоны разрешенных энергий разделены областями запрещенных энергий – запрещенными зонами. Нижнюю зону называют валентной, верхнюю – зоной проводимости.

По характеру заполнения зон электронами все тела делят на 3 класса: Ø Проводники Ø Полупроводники Ø Диэлектрики

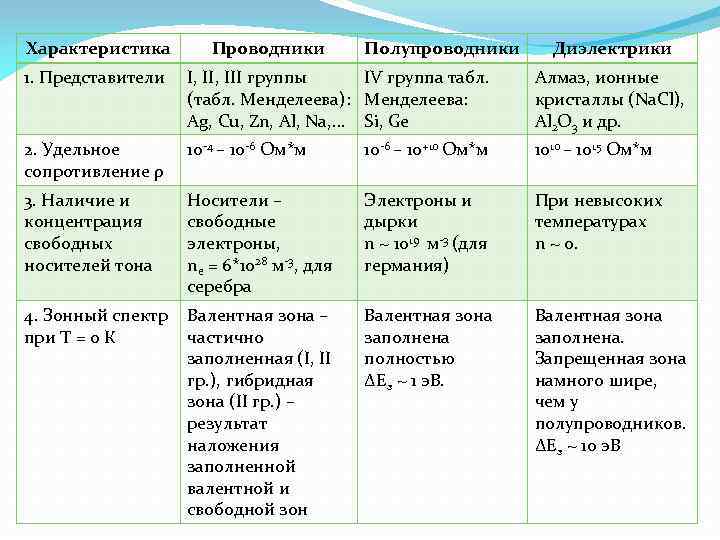Характеристика Проводники Полупроводники Диэлектрики 1. Представители I, III группы IV группа табл. (табл. Менделеева): Менделеева: Ag, Cu, Zn, Al, Na, … Si, Ge Алмаз, ионные кристаллы (Na. Cl), Al 2 O 3 и др. 2. Удельное сопротивление ρ 10 -4 – 10 -6 Ом*м 10 -6 – 10+10 Ом*м 1010 – 1015 Ом*м 3. Наличие и концентрация свободных носителей тона Носители – свободные электроны, ne = 6*1028 м-3, для серебра Электроны и дырки n ~ 1019 м-3 (для германия) При невысоких температурах n ~ 0. 4. Зонный спектр при T = 0 К Валентная зона – частично заполненная (I, II гр. ), гибридная зона (II гр. ) – результат наложения заполненной валентной и свободной зон Валентная зона заполнена полностью ∆Eз ~ 1 э. В. Валентная зона заполнена. Запрещенная зона намного шире, чем у полупроводников. ∆Eз ~ 10 э. В

Собственные полупроводники При Т = 0 К валентная зона укомплектована полностью, зона проводимости пустая. При Т = 0 собственные полупроводники и диэлектрики обладают нулевой проводимостью. С увеличением температуры часть электронов приобретают энергию, достаточную для преодоления запрещенной зоны и перехода в зону проводимости. При приложении к такому кристаллу внешнего поля в нем возникает направленное движение электронов.

Проводимость [σ] = Ом-1 * м-1 , удельная электропроводимость проводника У хороших проводников σ: 107 - 108 Ом-1 * м-1. У хороших диэлектриков σ: 10 -12 – 10 -14 Ом-1 * м-1. Удельное сопротивление ρ = 1/σ. Возникновение тока в проводниках свидетельствует о том, что под действием поля электроны приобретают направленное движение (дрейф), функция распределения их по состояниям изменяется.

Зависимость σ от Т В классической теории удельная электропроводность проводника: λ – длина свободного пробега электрона mn - эффективная масса электрона ν – число столкновений, в рез-те которых исчезает непрерывное движение электронов в данном направлении V – средняя скорость движения электронов n – концентрация электронной проводимости.

Как сказывается состояние электронного газа на его электропроводимости? Ø Для вырожденного газа – распределение Ферми. Дирака: λ = λФ – длина свободного пробега электронов, обладающих энергией Ферми VФ - скорость электронов νФ - число столкновений, в рез-те которых рассеиваются электроны в заданном направлении

Ø Для невырожденного газа – статистика Максвелла-Больцмана: - усреднение по всему коллективу ~ 1/Т n~ ~ . Тогда σ ~