Физика реального кристалла 10 Сдвиговая прочность кристаллов Модели

Физика реального кристалла 10. Сдвиговая прочность кристаллов. Модели ядра дислокаций. Барьер Пайерлса. Механизмы пластической деформации. Профессор Б. И. Островский ostr@cea. ru

Прочность кристаллов на сдвиг

Атомная структура ядра дислокации Пластичные материалы можно ковать! Fe, Cu – пластичны; ? ? Si, Ge – хрупки

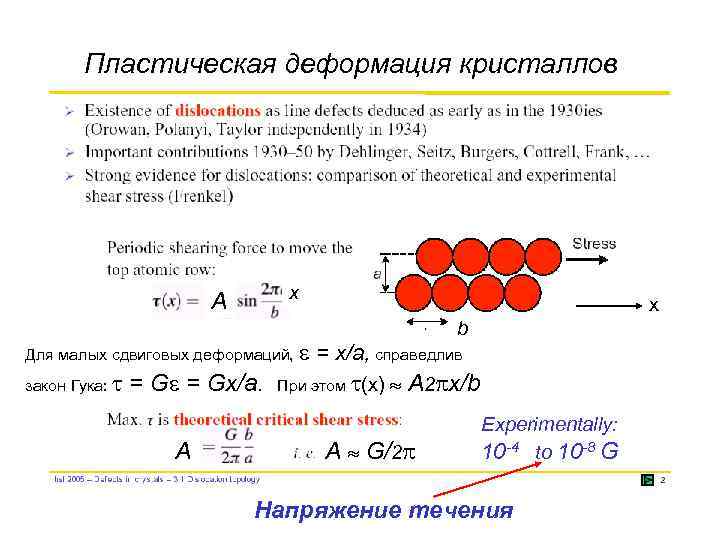Пластическая деформация кристаллов x A Для малых сдвиговых деформаций, закон Гука: = Gx/a. A x b = x/a, справедлив При этом (x) A 2 x/b A G/2 Experimentally: 10 -4 to 10 -8 G Напряжение течения

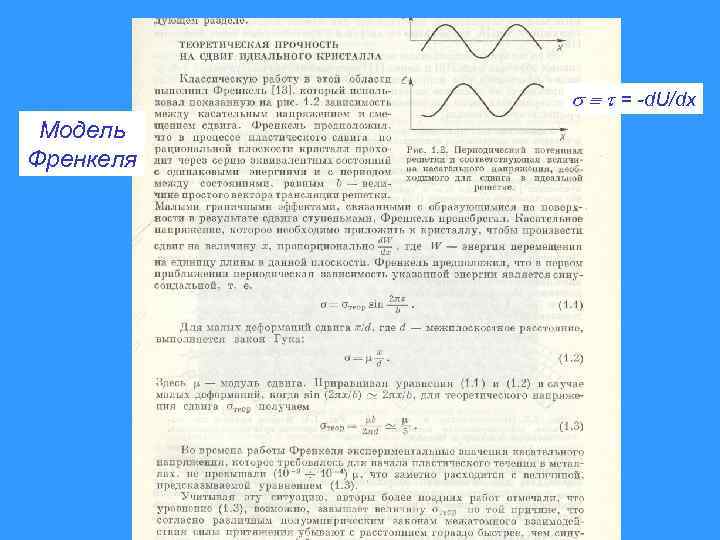= -d. U/dx Модель Френкеля

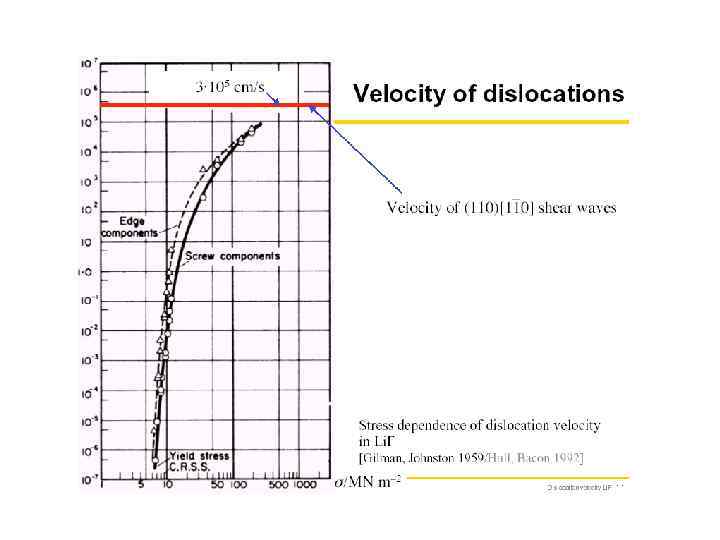
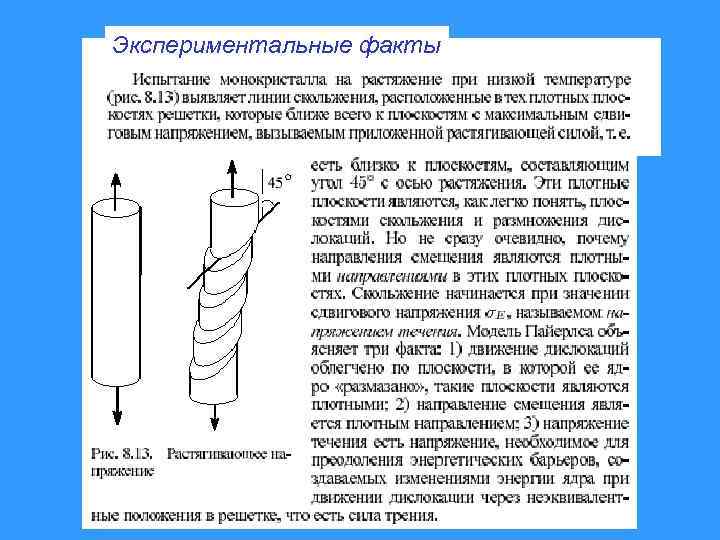Экспериментальные факты

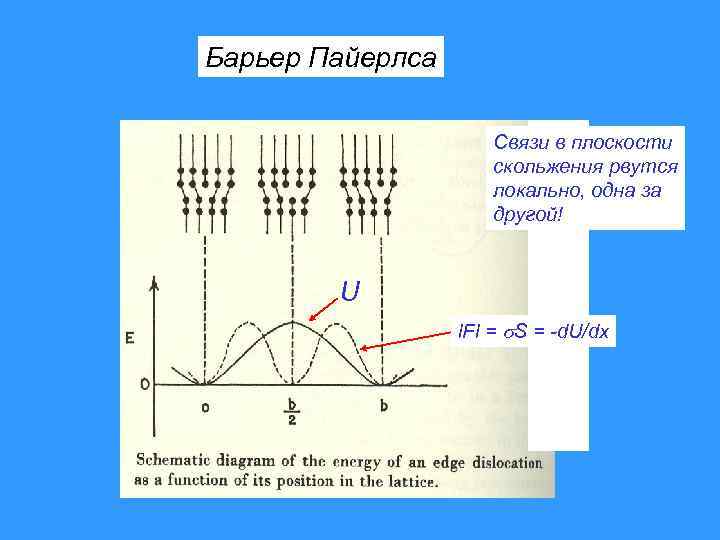Барьер Пайерлса Связи в плоскости скольжения рвутся локально, одна за другой! U l. Fl = S = -d. U/dx

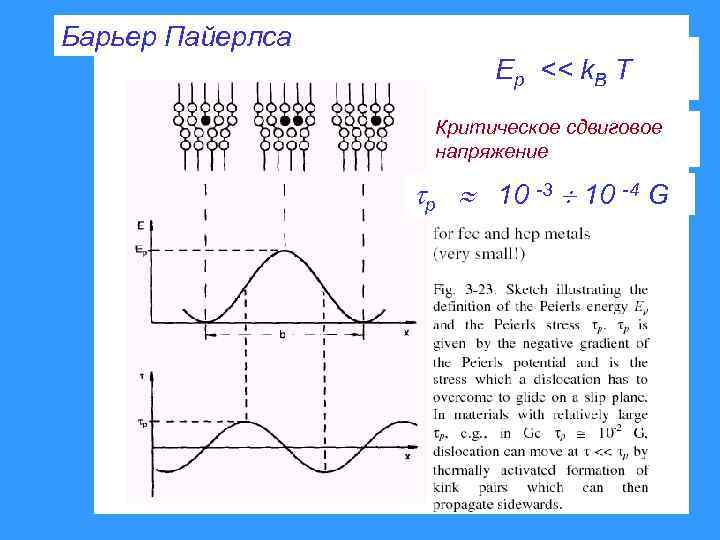Барьер Пайерлса Ep << k. B T Критическое сдвиговое напряжение p 10 -3 10 -4 G

Модель Пайерлса - Набарро «ширина» ядра дислокации

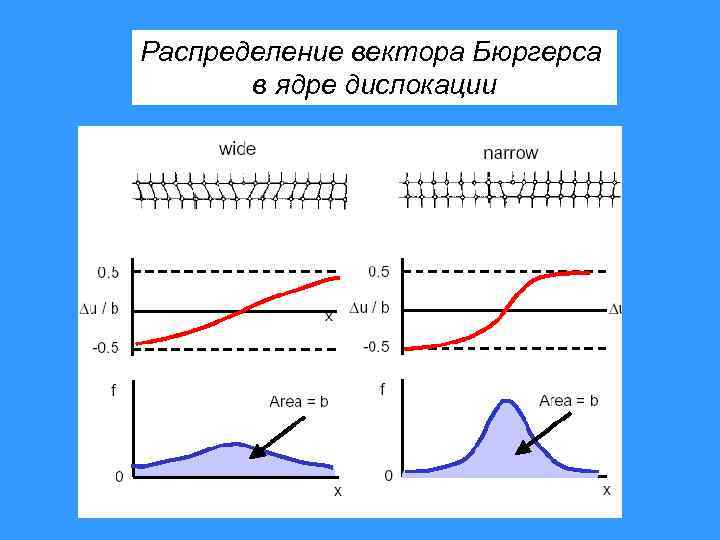Распределение вектора Бюргерса в ядре дислокации

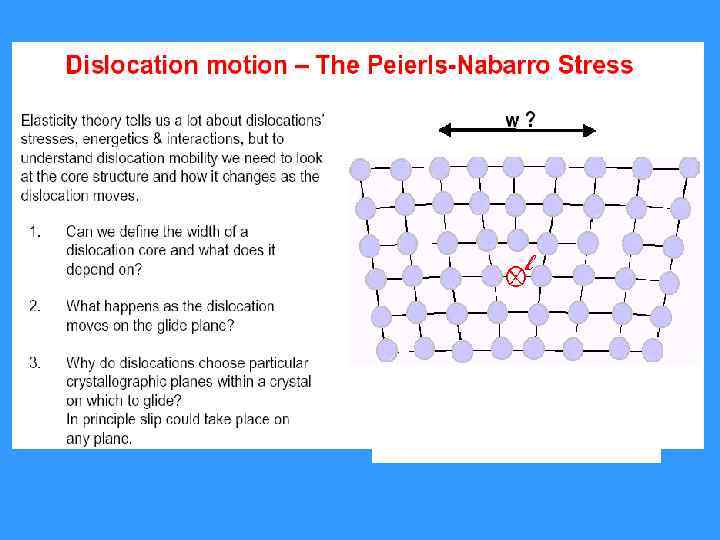
Чтобы получить кон-

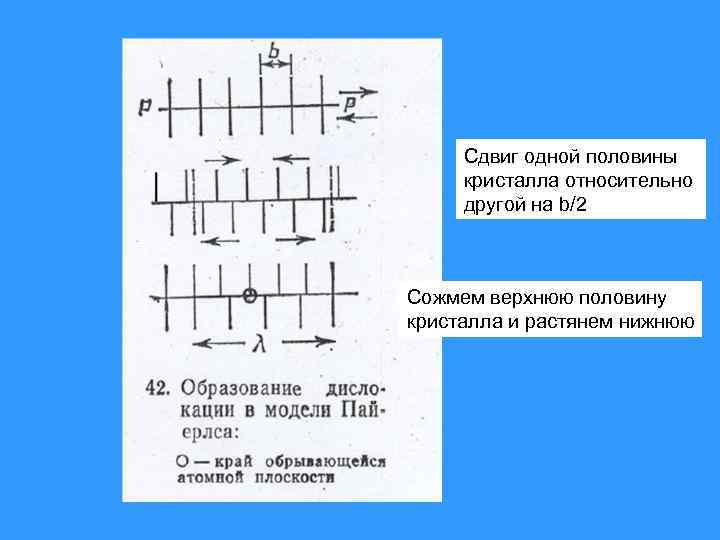Сдвиг одной половины кристалла относительно другой на b/2 Сожмем верхнюю половину кристалла и растянем нижнюю

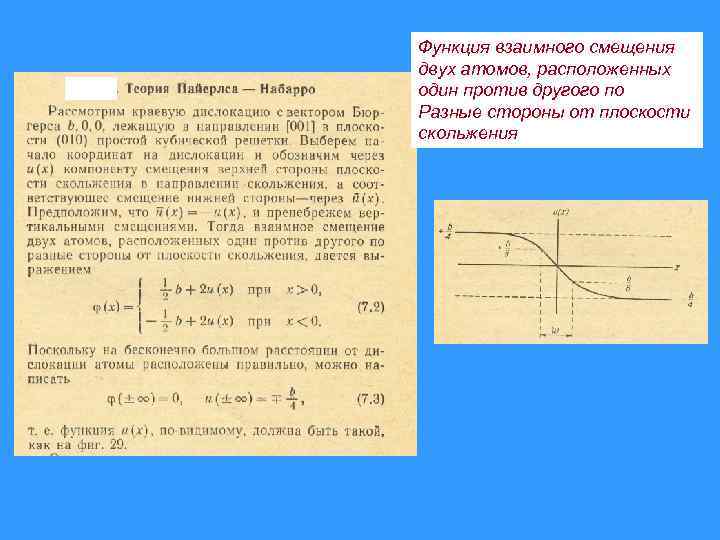Функция взаимного смещения двух атомов, расположенных один против другого по Разные стороны от плоскости скольжения

Расположение n одноименных дислокаций в плоскости скольжения = D = Gb/2 (1 - )

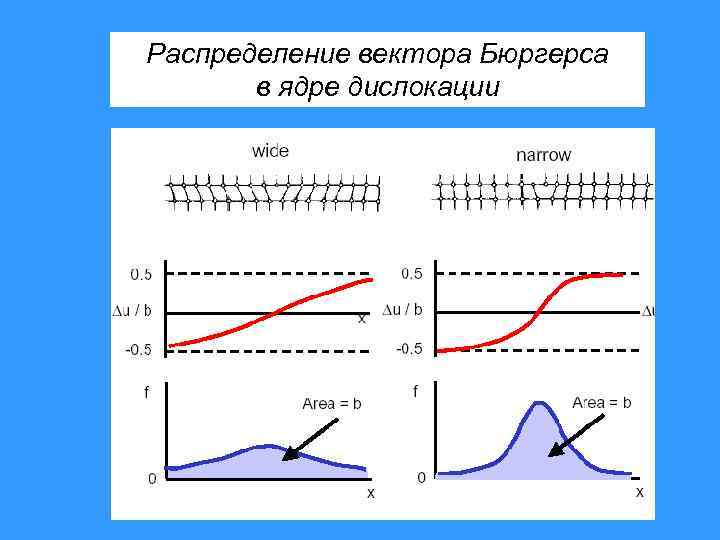Распределение вектора Бюргерса в ядре дислокации

(x) = (Gb/2 d)sin(2 /b)x (x) = Asin(2 x /b)x A Для малых сдвиговых деформаций, закон Гука: = Gx/d. A d x b = x/d, справедлив При этом (x) A 2 x/b A = Gb/2 d

D = Gb/2 (1 - ); для сдвиговых напряжений, полученных на основе континуального подхода Вольтерра b/4 - определяет «ширину» 2 ядра дислокации - b/4

Пайерловский рельеф кристалла

= d/2(1 - ) (3/4)d; 1/3 – exp(-3 d/b) 2 x 10 -4 (ГЦК решетка) d/b = 20. 32 b) Коэффициент Пуассона

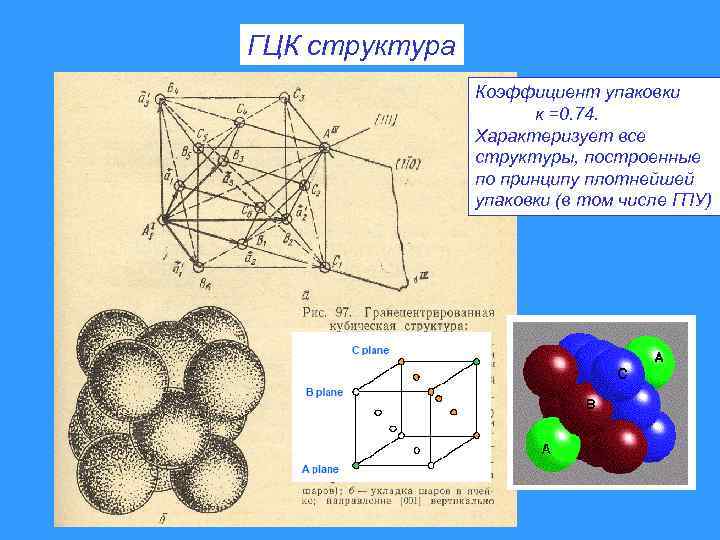ГЦК структура Коэффициент упаковки к =0. 74. Характеризует все структуры, построенные по принципу плотнейшей упаковки (в том числе ГПУ)

p 10 -4 G (ГЦК решетка) Ep = p b 2/2 10 -4 Gb 2 Что в пересчете на одну связь дает: Epbond 5 x 10 -4 эв Для сравнения: k. B T = 1. 4 10 -16 эрг/К x 300 К 4 x 10 -14 эрг 3 x 10 -2 эв

Оценки упругой энергии дислокации При обычных значениях плотности дислокаций =107 см-2, среднее расстояние между ними составляет R -1/2 3. 10 -4 см, что дает для и 10 полн /L = При G 1012 дин. см-2 и b = 2. 10 -8 см имеем: /L = 4. 10 -4 эрг/см полн Что в пересчете на одну связь дает: Ebond 4. 10 -4 эрг/см x 2. 10 -8 см = = 8. 10 -12 эрг 5 эв

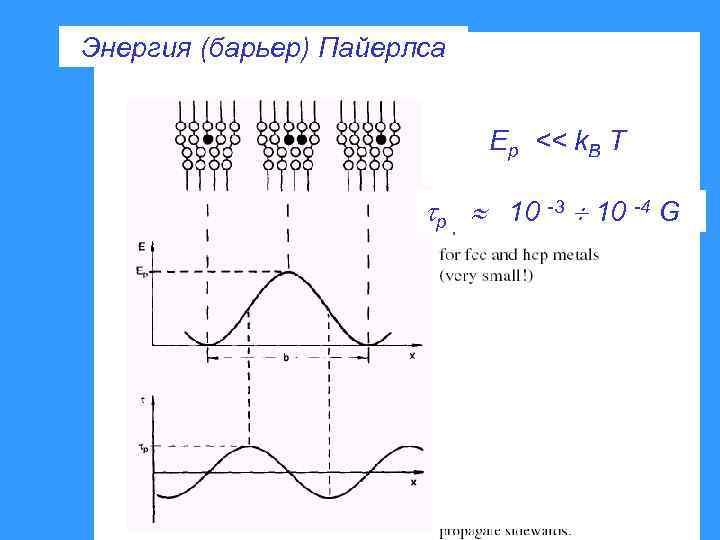Энергия (барьер) Пайерлса Ep << k. B T p 10 -3 10 -4 G

Summary p exp(-kd/a) a - min Пластическая деформация - движение и размножение дислокаций в плоскости скольжения

Дислокации в гранецентрированной кубической решетке Дислокационные сетки с тройными узлами

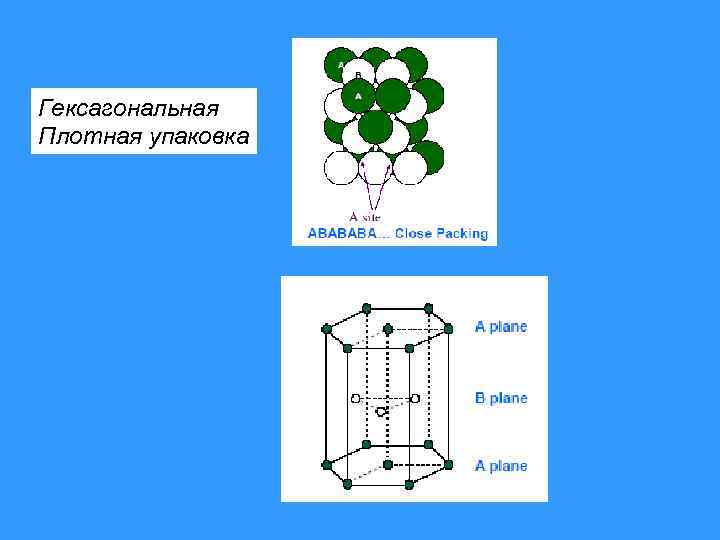Гексагональная Плотная упаковка

Common crystal structures in metals: – Face centered cubic (fcc): ABCABC… packing: Ni, Cu, Ag, Al, Au – Hexagonal close packed (hcp): ABABAB … packing: Mg, Zn, Co, Ti

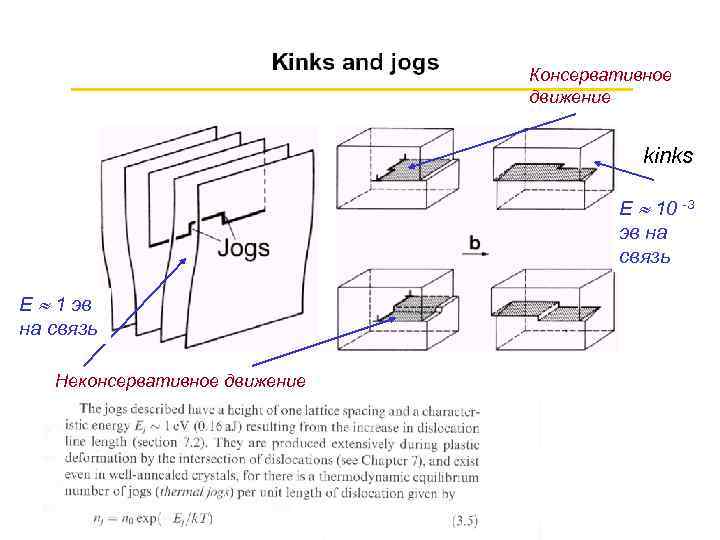Консервативное движение kinks Е 10 -3 эв на связь Е 1 эв на связь Неконсервативное движение

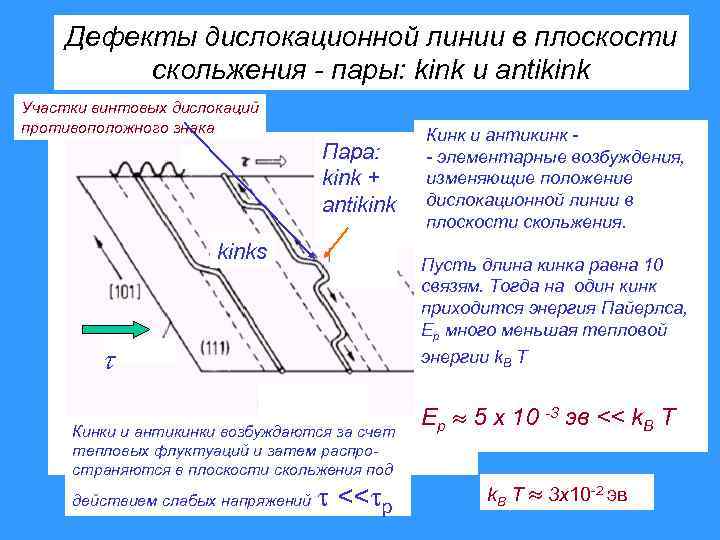Дефекты дислокационной линии в плоскости скольжения - пары: kink и antikink Участки винтовых дислокаций противоположного знака Пара: kink + antikinks Пусть длина кинка равна 10 связям. Тогда на один кинк приходится энергия Пайерлса, Ep много меньшая тепловой энергии k. B T Кинки и антикинки возбуждаются за счет тепловых флуктуаций и затем распространяются в плоскости скольжения под действием слабых напряжений Кинк и антикинк - элементарные возбуждения, изменяющие положение дислокационной линии в плоскости скольжения. << p Ep 5 x 10 -3 эв << k. B T 3 x 10 -2 эв

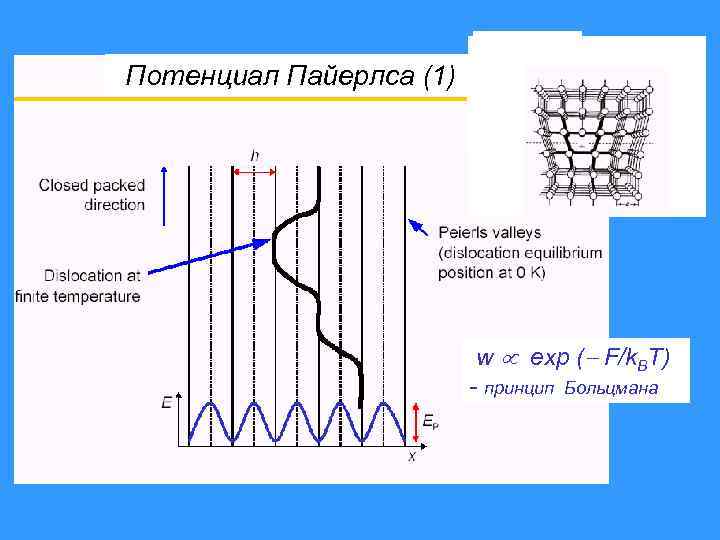Потенциал Пайерлса (1) w exp ( F/k. BT) - принцип Больцмана

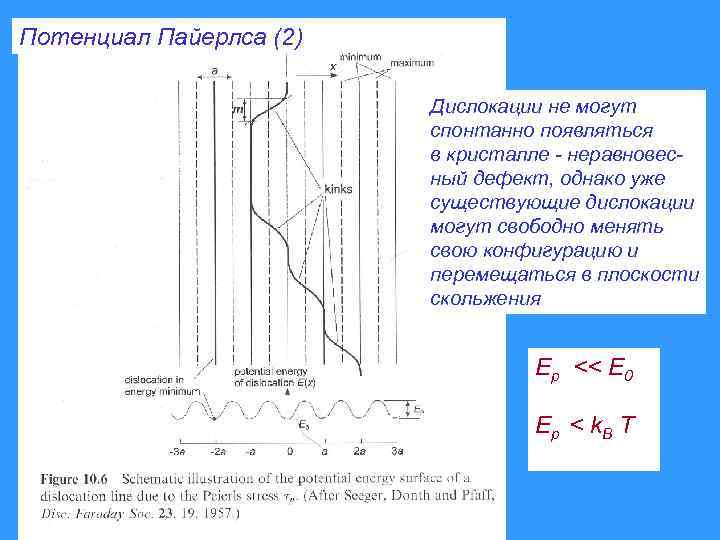Потенциал Пайерлса (2) Дислокации не могут спонтанно появляться в кристалле - неравновесный дефект, однако уже существующие дислокации могут свободно менять свою конфигурацию и перемещаться в плоскости скольжения Ep << E 0 Ep < k. B T

Заключительные замечания Необходимо отметить, что величины энергии Пайерлса Ep и критического напряжения сдвига p чрезвычайно чувствительны к природе межатомных сил и характеру упаковки атомов в элементарной ячейке. p 10 -4 10 -5 G p 10 -2 для ГЦК и ГПУ металлов; для ковалентных кристаллов типа кремния и алмаза