Физика полупроводников Основные понятия Ag Полупроводники Cu

Физика полупроводников Основные понятия

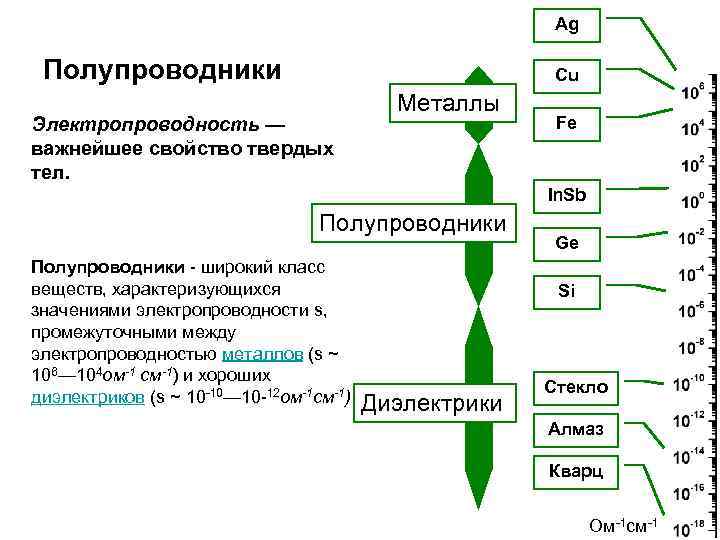Ag Полупроводники Cu Электропроводность — важнейшее свойство твердых тел. Металлы Fe In. Sb Полупроводники - широкий класс веществ, характеризующихся значениями электропроводности s, промежуточными между электропроводностью металлов (s ~ 106— 104 ом-1 см-1) и хороших диэлектриков (s ~ 10 -10— 10 -12 ом-1 см-1) Диэлектрики Ge Si Стекло Алмаз Кварц Ом-1 см-1

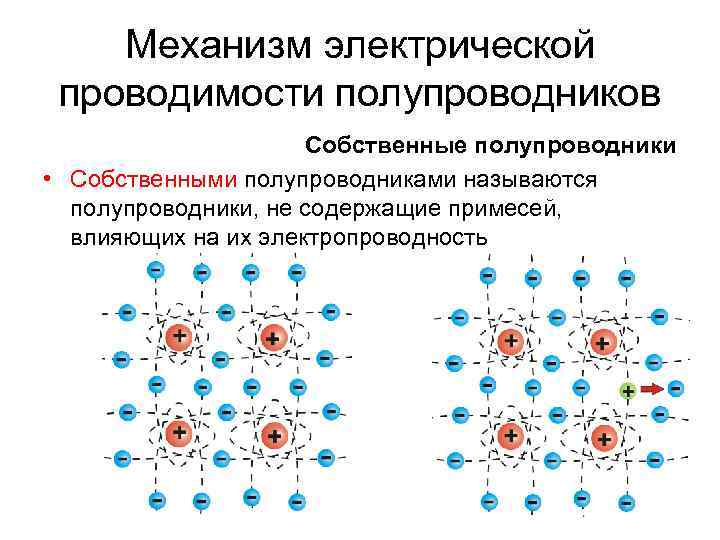Механизм электрической проводимости полупроводников Собственные полупроводники • Собственными полупроводниками называются полупроводники, не содержащие примесей, влияющих на их электропроводность

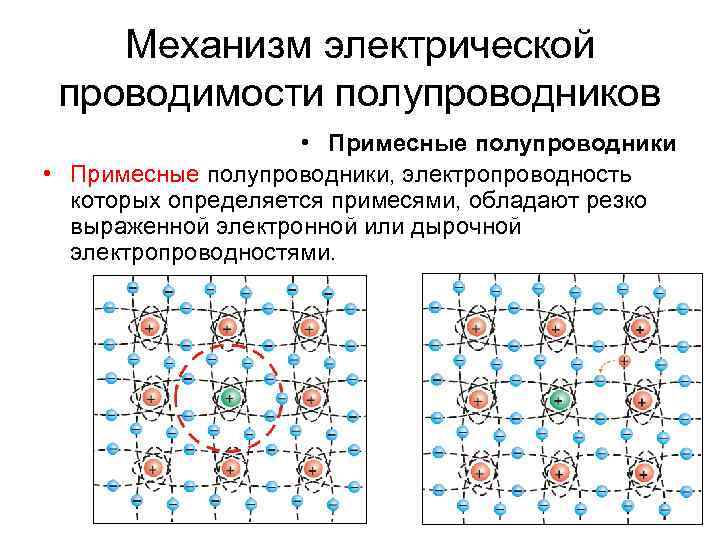Механизм электрической проводимости полупроводников • Примесные полупроводники, электропроводность которых определяется примесями, обладают резко выраженной электронной или дырочной электропроводностями.

Виды полупроводников По виду проводимости Электронные полупроводники (n-типа) Термин «n-тип» происходит от слова «negative» , обозначающего отрицательный заряд основных носителей. Этот вид полупроводников имеет примесную природу. В четырёхвалентный полупроводник (например, кремний) добавляют примесь пятивалентного полупроводника (например, мышьяка). Дырочные полупроводники (р-типа) Термин «p-тип» происходит от слова «positive» , обозначающего положительный заряд основных носителей. Этот вид полупроводников, кроме примесной основы, характеризуется дырочной природой проводимости. В четырёхвалентный полупроводник (например, в кремний) добавляют небольшое количество атомов трехвалентного элемента (например, бора).

Полупроводники простые полупроводниковые материалы — собственно химические элементы: бор B, углерод C, германий Ge, кремний Si сложные полупроводниковые материалы - химические соединения, обладающие полупроводниковыми свойствами и включающие в себя два, три и более химических элементов. AIII BV In. As, In. P, Ga. N,

Элементы зонной теории При большом количестве атомов более энергетические уровни расщепляются до практически непрерывных дискретных наборов — энергетических зон. Наивысшая из разрешённых энергетических зон в полупроводниках и диэлектриках, в которой при температуре 0 К все энергетические состояния заняты электронами, называется валентной зоной, следующая за ней — зоной проводимости.

Зонная диаграмма Зона проводимости — первая из незаполненных электронами зон (диапазонов энергии, где могут находиться электроны) Энергия Ферми может интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур Валентная зона — энергетическая область разрешённых электронных состояний в твёрдом теле, заполненная валентными электронами.

Статистика равновесных носителей заряда в полупроводниках.

Носителями заряда (тока) называют электроны зоны проводимости и дырки валентной зоны. В общем случае в полупроводнике могут содержаться примеси как донорного, так и акцепторного типов. В этом случае при T > 0 K 0 в результате теплового возбуждения электроны будут переходить в зону проводимости переходы (1, 2) и на акцепторные уровни переходы (3). 1 2 Ec 2’ Ed 1’ 1 Ea 3’ EV В результате тепловых переходов 1, 3, образуются носители заряда. Если бы тепловые переходы были единственными, то концентрация носителей заряда непрерывно возрастала бы со временем. С течением времени концентрация электронов была бы , однако эксперименты дают меньшее значение, это связано с тем, что наряду с тепловым возбуждением одновременно протекает обратный процесс – процесс рекомбинации. Это переходы носителей сверху вниз (переходы 1' – 3').

В адиабатическом приближении считается, что тепловое движение кристаллической решетки влияет на вероятность заполнения носителями заряда состояний в зонах, но не на сами состояния. В полупроводниках, как и металлах, вероятность заполнения электроном энергетического уровня с энергией определяется функцией распределения Ферми-Дирака: (1) где m- уровень химического потенциала. Эта функция распределения применима только к равновесным носителям заряда, что подчеркивается знаком 0. Из (1) следует, что при T = 0 K 0 все уровни с энергией e < m заполнены электронами , а при e > m уровни свободны от электронов. При T > 0 K 0 “ступенька” в функции распределения размывается и появляется хвост кривой распределения. При любой T > 0 K 0 вероятность заполнения уровня с энергией e = m согласно (1) равна ½. Значит, уровень химического потенциала это такой уровень, который с одинаковой вероятностью может быть заполнен электронами и свободен от них.

(2) функция распределения Ферми-Дирака для дырок. Известно, что объем первой зоны Бриллюэна равен . В зоне Бриллюэна число разрешенных волновых векторов N равно числу элементарных ячеек кристалла. Тогда, на одно разрешенное квантовое состояние будет приходиться объем обратного пространства равный: где V – объем кристалла. В кристаллах единичного объема на одно разрешенное состояние приходится объем обратного пространства равный . Впредь будем рассматривать кристаллы единичного объема. аналогичное выражение для числа состояний в кристаллах единичного объема, которые занимают электроны в интервале энергий от до . (3)

(4) – функция плотности состояний для электронов зоны проводимости. Она определяет собой число состояний в кристалле единичного объема приходящегося на единичный интервал энергии вблизи энергии. Для дырок валентной зоны функция распределения равна: (8) На рисунке площадь заштрихованного прямоугольника равна: и численно равна числу электронных состояний в интервале энергий.

Для непрямозонных полупроводников: германий, кремний выражение для функции плотности имеет вид: (9) где - эффективная масса плотности состояний, M – число полных эллипсоидов (долин) , MSi = 6, MGe = 4.

Связь уровня химического потенциала с концентрацией равновесных носителей заряда в невырожденных полупроводниках.

Очевидно, число электронов в кристалле единичного объема, занимающих состояния с энергиями в интервале от до будет равно (1) Сначала будем рассматривать случай когда (2) Условие должно выполняется для всех энергий электрона, в том числе и для минимальных энергий , т. е. отсюда следует, что в невырожденных полупроводниках уровень химического потенциала лежит ниже дна зоны проводимости на величину не меньшую .

Концентрация всех электронов будет равна: Так как под знаком интеграла стоит функция с быстро убывающей энергией, то верхний придел интегрирования можно заменить на бесконечность, тогда: (3) - эффективная плотность состояний в зоне проводимости численно равная концентрации электронов в зоне проводимости, при условии, что уровень совпадает с дном проводимости.

Аналогично можно получить выражение для концентрации дырок в невырожденном полупроводнике: (4) - эффективная плотность состояний в валентной зоне. Выражение (3) и (4) верны как для чистого, так и легированного примесями полупроводника.

Концентрация равновесных носителей заряда в собственных невырожденных полупроводниках.

В собственных полупроводниках носители заряда образуются за счет теплового возбуждения электронов валентной зоны. Концентрацию в собственных полупроводниках будем обозначать: (1) Известно, что в высокой температурной области ширина запрещенной зоны полупроводника уменьшается по линейному закону: (2) - ширина запрещенной зоны при T = 0 K 0. Подставим (2) в (1) (3) (3')

Таким образом, определяют ширину запрещенной зоны полупроводника отнесенную к абсолютному нулю температуры. Найдем положение химического потенциала в собственных невырожденных полупроводниках: (4) После сокращения и последующего логарифмирования получаем, что (5)

Из (5) следует, что: 1. Если , то при всех температурах , то при T = 0 . , если Видно, что уровень химического потенциала лежит точно по средине запрещенной зоны. 2. Если , то с ростом температуры уровень химического потенциала поднимается вверх от середины запрещенной зоны. 3. Если , то с ростом температуры уровень химического потенциала опускается вниз от середины запрещенной зоны.

Концентрация равновесных носителей заряда в невырожденных полупроводниках с одним типом мелких примесных центров и низких температурах

Рассмотрим полупроводник, содержащий мелкие донорные центры одного типа. Из зонной диаграммы видно, что электроны образуются за счет переходов 1 и 2, а дырки только за счет переходов 1. В таком полупроводнике очевидно концентрация электронов будет больше, чем концентрация дырок. 1 2 Ec Ed Ea EV 1. Закон действующих масс. Рассмотрим произведение концентраций носителей заряда, воспользовавшись общими соотношениями: (1) Соотношение (1) это закон действующих масс для носителей заряда в полупроводнике. Заметим, что для данного полупроводника при данной температуре величина . Из (1) следует что, если концентрация электронов увеличивается, то концентрация дырок должна уменьшаться, если , то полупроводник будет обладать монополярной электронной проводимостью или проводимостью n - типа.

2. Уравнение электронейтральности основывается на том, что в любом физически малом объеме полупроводника суммарный заряд всех заряженных частиц должен быть равен нулю. В полупроводнике донорного типа отрицательный заряд обеспечивается электронами зоны проводимости, а положительный дырками и положительно заряженными донорами. Будем обозначать концентрацию положительных доноров через , тогда уравнение электронейтральности для полупроводника n - типа будет иметь вид: (2) (3) Функция Ферми-Дирака определяет собой распределение зонных равновесных носителей заряда. Эта функция не применима для носителей заряда находящихся на примесных центрах.

Для зонных носителей заряда справедлив принцип Паули: на каждом уровне может находиться два носителя заряда с разными спинами. Сильное кулоновское отталкивание приводит к тому, что принцип Паули неприменим для таких носителей заряда. Вероятность заполнения примесных состояний электронами и дырками определяется следующими соотношениями: - вероятность заполнения электроном донорного уровня с энергией (незаряженный донор). - вероятность заполнения дыркой акцепторного уровня с энергией (незаряженный акцептор). - вероятность заполнения дыркой донорного уровня с энергией , отсюда следует, что донорный уровень положительно заряжен. - вероятность заполнения электронами уровня .

При очень низких температурах число тепловых переходов 1 очень мало, поэтому в уравнении (3) и величиной можно пренебречь, тогда уравнение электронейтральности примет вид: (4) можно записать: (4')

При низких температурах величина и тогда (5)

Из (5) следует, что при T = 0 уровень химического потенциала в монополярном полупроводнике n - типа лежит посредине между дном зоны проводимости и донорным уровнем . С ростом температуры химический потенциал поднимается вверх к уровню , затем опускается вниз пересекая уровень . Тогда концентрация электронов в зоне проводимости определяется из выражения: и с подстановкой в него (5), учитывая, что , получим (6) Таким образом, концентрация электронов в таком полупроводнике экспоненциально возрастает с ростом температуры. Найдем степень ионизации мелких доноров в тех условиях когда, уровень химического потенциала пересекает уровень : (7)

Подставим (7) в (6) и получим, что: Значит, когда уровень химического потенциала пересекает уровень , доноры истощены на половину, т. е. на половину ионизированы. Аналогично можно получить выражение для концентрации дырок в полупроводнике, содержащим только мелкие акцепторные центры: (8)

Концентрация равновесных носителей заряда в невырожденных полупроводниках с одним типом примесных уровней при высоких температурах

Рассмотрим полупроводники, содержащие только мелкие доноры. (1) В этом случае нельзя пренебрегать величиной p. При высоких температурах все доноры ионизированы, т. е. (2) (3) так как , то знак “-” следует отбросить (4)

Рассмотрим два случая в области высоких температур 1. Высокие промежуточные температуры. Когда , тогда из (4) следует, что: (5) В области этих температур концентрация электронов равна концентрации доноров и следовательно не зависит от температур – область истощения. Но в этой области температур концентрация дырок очень резко возрастает с температурой. (6)

2. Очень высокие температуры. Когда , тогда из (4) следует, что: (7) Значит, при высоких температурах концентрация электронов в зоне проводимости будет определяться собственными носителями заряда. (8) В этом случае будут наиболее актуальными тепловые переходы 1. Уровень химического потенциала при очень высоких температурах, как и в собственном полупроводнике, лежит по средине запрещенной зоны. На энергетической диаграмме показан качественный ход зависимости , в широком диапазоне температур в полупроводниках содержащих только мелкие доноры.

Таким образом, в полупроводниках содержащих один тип примесных мелких центров, например доноров, концентрация носителей заряда во всей температурной области исследования определяется следующими выражениями. 1. область низких температур. (9) 2. область промежуточных температур (область истощения доноров). (10)

3. Область высоких температур. (11) тогда Логарифмическая функция слабая, следовательно, в соотношениях (9) и (11) температурная зависимость будет определяться в основном вторым слагаемым.

Тогда в соотношениях (9) и (11) температурная зависимость концентрации электронов выражается в координатах: , будет представлять собой прямую линию отражены на рисунке. . Зависимости (9) и (11) По величине концентрации электронов в области истощения можно определить концентрацию введенных в полупроводник мелких доноров Область низких температур: , - подвижность электронов, скорость направленного движения заряда в единичном электрическом поле, - электропроводность. Область промежуточных температур: Полупроводники, у которых имеется один тип примесных центров называется некомпенсированным полупроводником.

Концентрация равновесных носителей заряда в полупроводниках с двумя типами примесных центров и их полной компенсации.

На практике чаще встречаются полупроводники, содержащие как мелкие доноры, так и мелкие акцепторы. На рисунке показана зонная схема и схема тепловых переходов в таком полупроводнике. При T > 0 K 0 в таком полупроводнике могут иметь место тепловые переходы 1 – 4 приводящие к образованию электронов и дырок. Очевидно, примесные переходы 4 будут мало актуальными, потому что энергия активации для таких переходов , так концентрация примесных атомов значительно меньше, чем собственных атомов то число переходов 4 в единицу времени будет значительно меньше, чем переходов 3, поэтому переходами 4 можно пренебречь. Запишем уравнение электронейтральности для полупроводника, имеющего мелкие доноры и акцепторы, исходя из условия, что в любом физически малом объеме полупроводника суммарный заряд всех частиц равен нулю. Будем рассматривать единичный объем кристалла. Отрицательный заряд в таком объеме создается свободными электронами с концентрацией n и отрицательно заряженными акцепторами . Положительный заряд обеспечивается p и . Тогда уравнение электронейтральности примет вид:

Пусть Примесные электроны зоны проводимости, появившиеся за счет переходов 1, блуждая по кристаллу, встречаются с примесными дырками, появившееся за счет переходов 2 и рекомбинируют. Рекомбинация происходит с образованием, как показано выше собственных атомов, а не их примесных центров, следовательно, за время порядка с момента нагревания полупроводника все примесные центры мелких доноров и акцепторов опустошаются, т. е. все мелкие доноры заряжаются положительно, а мелкие акцепторы отрицательно. Они перестают быть электрически активными, т. е. не являются поставщиками электронов и дырок в свои зоны, значит в этих условиях Тогда уравнение электронейтральности примет вид:

Значит электропроводность полностью компенсированного полупроводника, является собственной электропроводностью. Число носителей заряда в таком полупроводнике будет таким же, как в чистом полупроводнике при прочих равных условиях. Однако другие физические характеристики такого полупроводника отличаются от чистого полупроводника. Полностью компенсированный полупроводник содержит два типа полностью заряженных примесных центров. Они являются эффективными рассеивателями носителей заряда. Подвижность носителей заряда в таких полупроводниках будет значительно ниже, чем подвижность в чистых полупроводниках.

Равновесная концентрация носителей заряда в частично компенсированных невырожденных полупроводниках.

Пусть В этом случае мелкие доноры и мелкие акцепторы в количестве будут взаимно компенсированы, т. е. все акцепторы будут заполнены электронами пришедшими с донорных центров, следовательно Число некомпенсированных доноров способных участвовать в тепловой генерации электронов в с – зону будет равно: - эффективная концентрация доноров. Значит, при соотношении полупроводник ведет себя как полупроводник - типа. В таком полупроводнике нет примесных дырок, а есть дырки образуемые в результате собственных переходов при высоких температурах. Уравнение электронейтральности для такого полупроводника с учетом предыдущего параграфа будет иметь вид: (1)

Рассмотрим несколько придельных случаев. 1. Очень низкие температуры В этом случае , . Тогда уравнение электронейтральности примет вид: (2) (3) 1. 2. 3. Подставим (3) в выражение для n , получим Видно, что энергия активации

2. Низкие температуры. В этом случае , . Тогда уравнение электронейтральности примет вид: (5) - концентрация доноров занятых электронами. (6) - эффективная концентрация ионизированных доноров (7) Видно, что энергия активации

3. Высокие температуры В этом случае нельзя пренебрегать величиной , . Тогда уравнение электронейтральности примет вид: (8) При высоких температурах: (9) По величине n, в этой области можно определить эффективную концентрацию 4. Очень высокие температуры (10)

Условие перехода полупроводника в вырожденное состояние и равновесная концентрация носителей заряда в полностью вырожденном полупроводнике

Рассмотрим некомпенсированный полупроводник n - типа, условие перехода такого полупроводника в вырожденное состояние будем считать равенство (для p типа ). Как известно уровень химического потенциала принимает максимальное значение при низких температурах, когда описывается соотношением: (1) Найдем концентрацию доноров , удовлетворяющие условию перехода полупроводника в вырожденное состояние . Для этого сначала найдем температуру соответствующую максимальному значению функции . Для этого найдем: (2)

(3) Максимальное значение : Тогда согласно соотношениям (2) и (3) (4) Найдем критическую концентрацию доноров, положив

(5) если выражать в э. В, а в единицах массы свободного электрона Из соотношения (5) следует, что наиболее выгодными материалами для создания вырожденных состояний являются такие полупроводники, которые имеют малую энергию ионизации примесей и малые эффективные массы.

Условие , есть условие перехода полупроводника n - типа в вырожденное состояние, но это не есть полностью вырожденный полупроводник, в котором концентрация электронов не должна зависеть от температуры (как в металле). Исследования показывают, что полупроводник полностью вырожден если , т. е. уровень химического потенциала должен лежать в зоне проводимости на расстоянии ее дна . Найдем концентрацию электронов в полностью вырожденном полупроводнике n- типа . Для этого мы должны использовать квантовую статистику Ферми-Дирака. (6)