физика металлов лекции pp2010.pptx
- Количество слайдов: 175
 Физика металлов Павлюкова Дарья Викторовна
Физика металлов Павлюкова Дарья Викторовна
 Введение Курс «Физика металлов» является синтезом двух фундаментальных наук – физики и металловедения. Основной раздел – физика твердого тела, изучающая строение и свойства твердых тел. Физика металлов – частный случай. Она объединяет вопросы кристаллографии, кристаллохимии, фазовых равновесий в сплавах. Материал разбит на 2 основные группы: 1. Атомно-электронное строение металлов 2. Физические и механические свойства металлов и сплавов
Введение Курс «Физика металлов» является синтезом двух фундаментальных наук – физики и металловедения. Основной раздел – физика твердого тела, изучающая строение и свойства твердых тел. Физика металлов – частный случай. Она объединяет вопросы кристаллографии, кристаллохимии, фазовых равновесий в сплавах. Материал разбит на 2 основные группы: 1. Атомно-электронное строение металлов 2. Физические и механические свойства металлов и сплавов
 План лекций I Атомно-электронное строение металлов • Силы связи и типы межатомного взаимодействия в кристаллах • Кристаллическая структура металлов • Структура расплавов и кристаллизация • Фазы в сплавах • Дефекты кристаллической структуры • Диффузия в металлах и сплавах
План лекций I Атомно-электронное строение металлов • Силы связи и типы межатомного взаимодействия в кристаллах • Кристаллическая структура металлов • Структура расплавов и кристаллизация • Фазы в сплавах • Дефекты кристаллической структуры • Диффузия в металлах и сплавах
 Баллы • 17 лекций: 1 лекция = 1 балл • 16 практических занятий: 1 практика = 1… 2 балла • РГР: 15 неделя - 30 баллов; 16 неделя – 30 -2 баллов и т. д. • Зачет: 20 баллов
Баллы • 17 лекций: 1 лекция = 1 балл • 16 практических занятий: 1 практика = 1… 2 балла • РГР: 15 неделя - 30 баллов; 16 неделя – 30 -2 баллов и т. д. • Зачет: 20 баллов
 Силы связи и типы межатомного взаимодействия в кристаллах
Силы связи и типы межатомного взаимодействия в кристаллах
 Силы Ван-дер-Ваальса •
Силы Ван-дер-Ваальса •
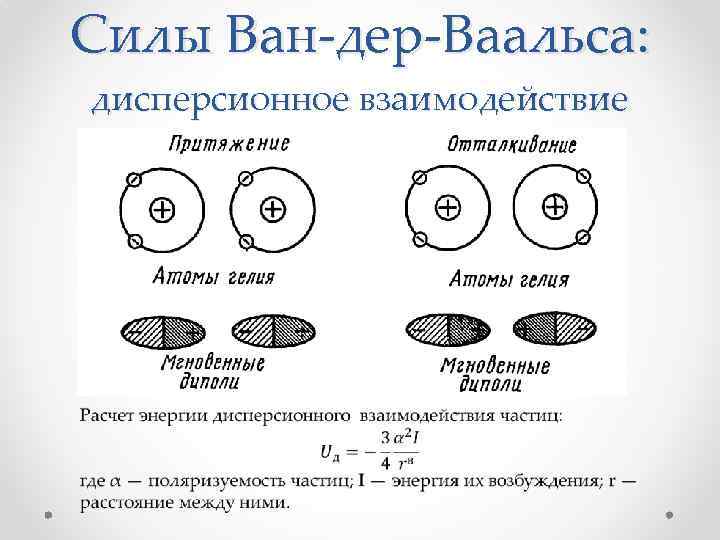 Силы Ван-дер-Ваальса: дисперсионное взаимодействие
Силы Ван-дер-Ваальса: дисперсионное взаимодействие
 Силы Ван-дер-Ваальса: ориентационное взаимодействие Энергия взаимодействия при низкой температуре и полной ориентации молекул: Энергия взаимодействия дипольных молекул при высокой температуре :
Силы Ван-дер-Ваальса: ориентационное взаимодействие Энергия взаимодействия при низкой температуре и полной ориентации молекул: Энергия взаимодействия дипольных молекул при высокой температуре :
 Силы Ван-дер-Ваальса: индукционное взаимодействие Энергия взаимного притяжения, возникающая вследствие взаимодействия между жестким диполем первой молекулы и индуцированным диполем второй молекулы: Где М — постоянный дипольный момент молекулы, α — ее поляризуемость.
Силы Ван-дер-Ваальса: индукционное взаимодействие Энергия взаимного притяжения, возникающая вследствие взаимодействия между жестким диполем первой молекулы и индуцированным диполем второй молекулы: Где М — постоянный дипольный момент молекулы, α — ее поляризуемость.
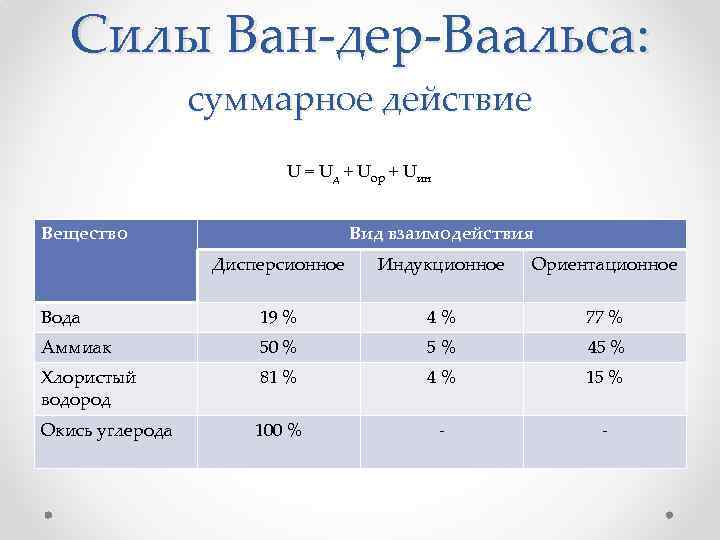 Силы Ван-дер-Ваальса: суммарное действие U = Uд + Uop + Uин Вещество Вид взаимодействия Дисперсионное Индукционное Ориентационное Вода 19 % 4 % 77 % Аммиак 50 % 5 % 45 % Хлористый водород 81 % 4 % 15 % Окись углерода 100 % - -
Силы Ван-дер-Ваальса: суммарное действие U = Uд + Uop + Uин Вещество Вид взаимодействия Дисперсионное Индукционное Ориентационное Вода 19 % 4 % 77 % Аммиак 50 % 5 % 45 % Хлористый водород 81 % 4 % 15 % Окись углерода 100 % - -
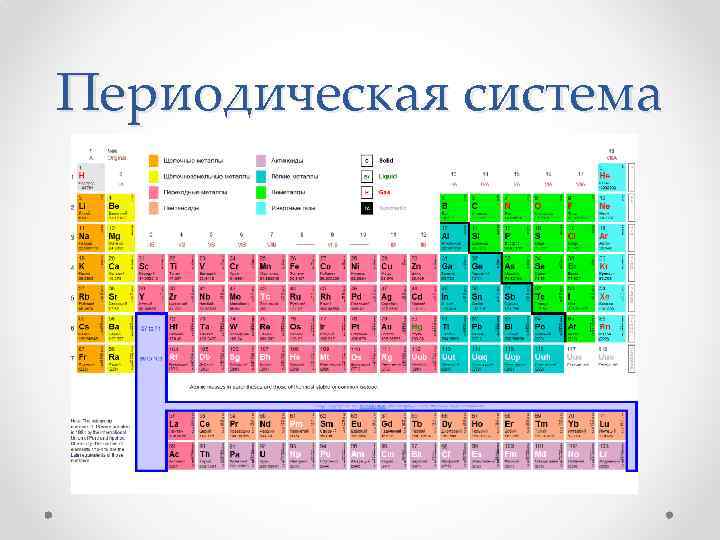 Периодическая система
Периодическая система
 Ионная связь где q – заряд ионов, r - расстояние. Энергия отталкивания: Uот = B/rn где В и n - постоянные. Результирующая энергия взаимодействия ионов:
Ионная связь где q – заряд ионов, r - расстояние. Энергия отталкивания: Uот = B/rn где В и n - постоянные. Результирующая энергия взаимодействия ионов:
 Ковалентная связь Расчет энергии атома водорода:
Ковалентная связь Расчет энергии атома водорода:
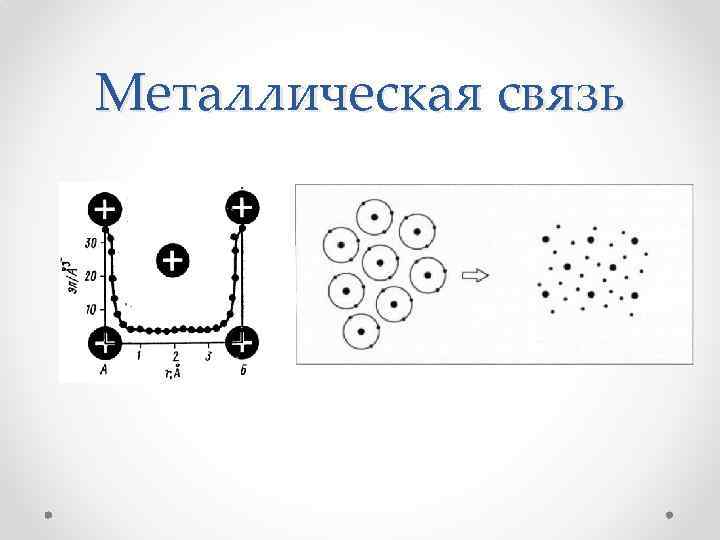 Металлическая связь
Металлическая связь
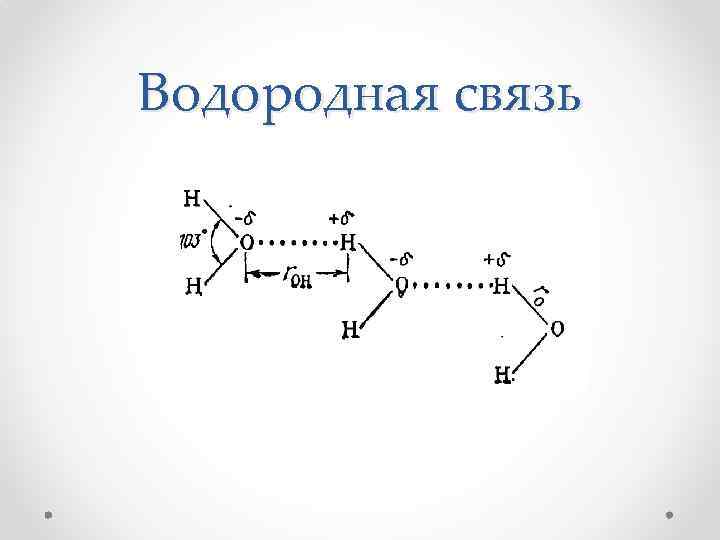 Водородная связь
Водородная связь
 Сопоставление различных видов связи • Связь Ван-дер-Ваальса: энергия 104 Дж/моль; жидкое и твердое состояние инертных газов, водорода, кислорода, азота. • Ионная связь: энергия 106 Дж/моль; неорганические соединения: металлы с галоидами, оксиды металлов, сульфиды, карбиды, нитриды. • Валентная связь: энергия 106 Дж/моль; органические и некоторые неорганические соединения (некоторые металлы и интерметаллические соединения). • Металлическая связь: энергия 106 Дж/моль; металлы и некоторые интерметаллические соединения. • Водородная связь: энергия 103 Дж/моль.
Сопоставление различных видов связи • Связь Ван-дер-Ваальса: энергия 104 Дж/моль; жидкое и твердое состояние инертных газов, водорода, кислорода, азота. • Ионная связь: энергия 106 Дж/моль; неорганические соединения: металлы с галоидами, оксиды металлов, сульфиды, карбиды, нитриды. • Валентная связь: энергия 106 Дж/моль; органические и некоторые неорганические соединения (некоторые металлы и интерметаллические соединения). • Металлическая связь: энергия 106 Дж/моль; металлы и некоторые интерметаллические соединения. • Водородная связь: энергия 103 Дж/моль.
 Силы отталкивания
Силы отталкивания
 Кристаллическая решетка
Кристаллическая решетка
 Понятие кристалла Кристаллы – твердые тела, в которых атомы или молекулы расположены дискретно и упорядоченно, то есть образуют пространственную кристаллическую решетку. Монокристалл – это кристаллический индивид, имеющий во всем объеме единую кристаллическую решетку. Поликристалл – совокупность мелких монокристаллов, различным образом ориентированных в пространстве.
Понятие кристалла Кристаллы – твердые тела, в которых атомы или молекулы расположены дискретно и упорядоченно, то есть образуют пространственную кристаллическую решетку. Монокристалл – это кристаллический индивид, имеющий во всем объеме единую кристаллическую решетку. Поликристалл – совокупность мелких монокристаллов, различным образом ориентированных в пространстве.
 Элементарная ячейка – минимальный по объему элемент решетки (группа атомов), пространственным перемещением (трансляцией) которого можно построить всю решетку кристалла. Решетка, полученная трансляцией частицы вдоль трех осей OX на отрезки а, 2 а, 3 а. . . ma; OY на отрезки b, 2 b, 3 b…nb; OZ на отрезке с, 2 с, 3 с…pc. Вектором r определяется положение любой частицы в такой решетке: r = ma + nb + pc; a, b, c – наименьшие векторы трансляции, их численные величины – периоды трансляции.
Элементарная ячейка – минимальный по объему элемент решетки (группа атомов), пространственным перемещением (трансляцией) которого можно построить всю решетку кристалла. Решетка, полученная трансляцией частицы вдоль трех осей OX на отрезки а, 2 а, 3 а. . . ma; OY на отрезки b, 2 b, 3 b…nb; OZ на отрезке с, 2 с, 3 с…pc. Вектором r определяется положение любой частицы в такой решетке: r = ma + nb + pc; a, b, c – наименьшие векторы трансляции, их численные величины – периоды трансляции.
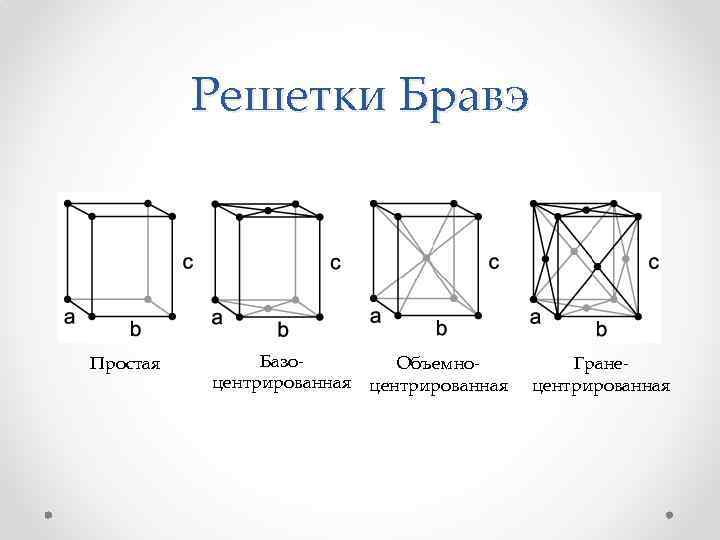 Решетки Бравэ Простая Базо. Объемноцентрированная Гранецентрированная
Решетки Бравэ Простая Базо. Объемноцентрированная Гранецентрированная
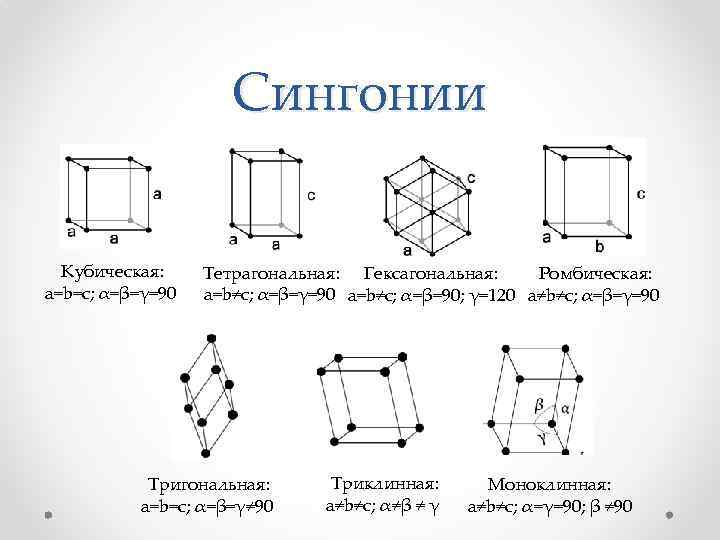 Сингонии Кубическая: a=b=c; α=β=γ=90 Тетрагональная: Гексагональная: Ромбическая: a=b≠c; α=β=γ=90 a=b≠c; α=β=90; γ=120 a≠b≠c; α=β=γ=90 Тригональная: a=b=c; α=β=γ≠ 90 Триклинная: a≠b≠c; α≠β ≠ γ Моноклинная: a≠b≠c; α=γ=90; β ≠ 90
Сингонии Кубическая: a=b=c; α=β=γ=90 Тетрагональная: Гексагональная: Ромбическая: a=b≠c; α=β=γ=90 a=b≠c; α=β=90; γ=120 a≠b≠c; α=β=γ=90 Тригональная: a=b=c; α=β=γ≠ 90 Триклинная: a≠b≠c; α≠β ≠ γ Моноклинная: a≠b≠c; α=γ=90; β ≠ 90
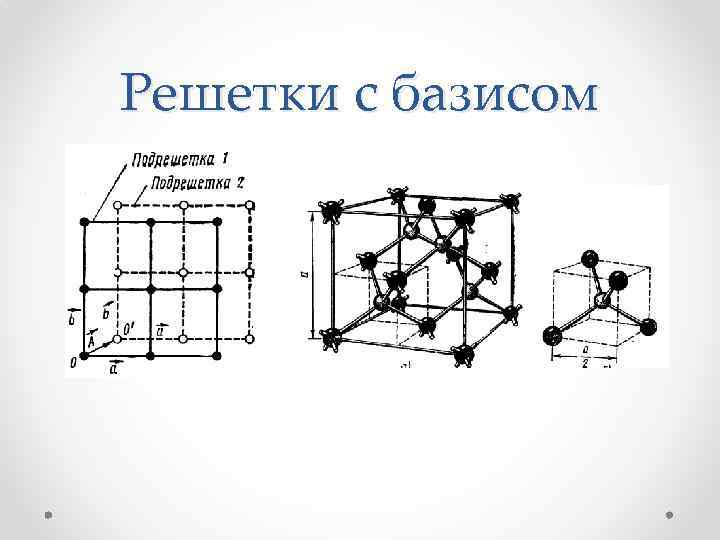 Решетки с базисом
Решетки с базисом
 Индексы Миллера • Индексы узлов: определение координат: x, y, z, x = ma, y = nb, z = pc, где a, b, c – параметры решетки; m, n, p – целые числа. Если a, b, c = 1, то индексы узла m, n, p [[mnp]]. Для отрицательного индекса х = -2 a; y = -1 b; z = 3 c Например: [[231]]
Индексы Миллера • Индексы узлов: определение координат: x, y, z, x = ma, y = nb, z = pc, где a, b, c – параметры решетки; m, n, p – целые числа. Если a, b, c = 1, то индексы узла m, n, p [[mnp]]. Для отрицательного индекса х = -2 a; y = -1 b; z = 3 c Например: [[231]]
 Индексы Миллера • Индексы направления представляют собой три наименьших целых числа, характеризующих положение ближайшего узла, лежащего на данном направлении. Ее положение однозначно определяется индексами [[mnp]] первого узла, через который она проходит.
Индексы Миллера • Индексы направления представляют собой три наименьших целых числа, характеризующих положение ближайшего узла, лежащего на данном направлении. Ее положение однозначно определяется индексами [[mnp]] первого узла, через который она проходит.
 Индексы Миллера •
Индексы Миллера •
 Индексы Миллера • Индексы плоскости гексагональных кристаллов: четырехосная система координат, 3 оси в основании, угол 120, 4 ось перпендикулярна. Обозначение: (hkil); I вычисляется: i = — (h + k).
Индексы Миллера • Индексы плоскости гексагональных кристаллов: четырехосная система координат, 3 оси в основании, угол 120, 4 ось перпендикулярна. Обозначение: (hkil); I вычисляется: i = — (h + k).
 Элементы симметрии • Триклинная: нет симметрии • Моноклинная: одна ось II-го порядка Ромбическая: три взаимно-перпендикулярных оси II-го порядка • Тетрагональная: одна ось IV-го порядка • Тригональная: одна ось III-го порядка • Гексагональная: одна ось VI-го порядка • Кубическая: четыре оси III-го порядка (диагонали) и три оси IV порядка Обозначение осей: 233; Инверсия: цифра; Отражение в плоскости: m; Инверсионный поворот: цифра, подчеркнутая сверху.
Элементы симметрии • Триклинная: нет симметрии • Моноклинная: одна ось II-го порядка Ромбическая: три взаимно-перпендикулярных оси II-го порядка • Тетрагональная: одна ось IV-го порядка • Тригональная: одна ось III-го порядка • Гексагональная: одна ось VI-го порядка • Кубическая: четыре оси III-го порядка (диагонали) и три оси IV порядка Обозначение осей: 233; Инверсия: цифра; Отражение в плоскости: m; Инверсионный поворот: цифра, подчеркнутая сверху.
 Химическая связь и металлическое состояние вещества
Химическая связь и металлическое состояние вещества
 Признаки металлов • Все особые физические свойства последних в большей или меньшей степени связаны с присутствием электронов проводимости; • Металл в твердом состоянии представляет собой совокупность ионов, образующих кристаллическую решетку, и электронов проводимости, движущихся внутри решетки и взаимодействующих как с ионами, расположенными в узлах решетки, так и друг с другом. Зависимость от внешнего электрического поля; • Особый характер температурной зависимости электропроводности при низких температурах, достаточно близких к 0 К. В то время как электропроводность неметаллов с приближением к 0 К уменьшается, у металлов она возрастает.
Признаки металлов • Все особые физические свойства последних в большей или меньшей степени связаны с присутствием электронов проводимости; • Металл в твердом состоянии представляет собой совокупность ионов, образующих кристаллическую решетку, и электронов проводимости, движущихся внутри решетки и взаимодействующих как с ионами, расположенными в узлах решетки, так и друг с другом. Зависимость от внешнего электрического поля; • Особый характер температурной зависимости электропроводности при низких температурах, достаточно близких к 0 К. В то время как электропроводность неметаллов с приближением к 0 К уменьшается, у металлов она возрастает.
 Металлическое состояние вещества Следует отметить, что правильнее говорить о металлическом состоянии вещества, т. к. некоторые вещества обладают металлическими свойствами только в определенной аллотропической модификации и при некоторых определенных температурах и давлениях. Поведение электронов проводимости объясняется коллективизацией электронов.
Металлическое состояние вещества Следует отметить, что правильнее говорить о металлическом состоянии вещества, т. к. некоторые вещества обладают металлическими свойствами только в определенной аллотропической модификации и при некоторых определенных температурах и давлениях. Поведение электронов проводимости объясняется коллективизацией электронов.
 Теория свободных электронов в металлах Электроны проводимости образуют идеальный электронный газ, подчиняющийся обычным газовым законам. Согласуется с законами квантовой статистики. 1900 – 1905 гг. – формулировка теории. 1927 г. – дальнейшее развитие.
Теория свободных электронов в металлах Электроны проводимости образуют идеальный электронный газ, подчиняющийся обычным газовым законам. Согласуется с законами квантовой статистики. 1900 – 1905 гг. – формулировка теории. 1927 г. – дальнейшее развитие.
 *Строение атома и теории электронов • К концу 19 века: электроны в металлах ведут себя как свободные; • К началу 20 века: электроны в металлах свободные частицы, электрический ток направленное и упорядоченное движение заряженных частиц под действием внешнего электрического поля; • Резерфорд: атомы состоят из ядра и электронной оболочки. Ядро несет положительный заряд, а электронная оболочка – отрицательный;
*Строение атома и теории электронов • К концу 19 века: электроны в металлах ведут себя как свободные; • К началу 20 века: электроны в металлах свободные частицы, электрический ток направленное и упорядоченное движение заряженных частиц под действием внешнего электрического поля; • Резерфорд: атомы состоят из ядра и электронной оболочки. Ядро несет положительный заряд, а электронная оболочка – отрицательный;
 *Строение атома и теории электронов • Бор: теоретическое обоснование атомной модели. электроны двигаются по стационарным орбитам, где они не излучают энергию, однако, при переходе с орбиты на орбиту они могут излучать или поглощать энергию. В качестве стационарных орбит Бором приняты окружности, на которых момент количества движения, т. е. момент импульса, равен целому числу приведенных постоянных Планка. Уравнения для стационарной орбиты и энергии электрона на этой орбите: где n – номер орбиты; ћ – приведенная постоянная Планка, me – масса электрона, e – заряд электрона, Z – количество протонов в ядре, ε 0 – диэлектрическая постоянная.
*Строение атома и теории электронов • Бор: теоретическое обоснование атомной модели. электроны двигаются по стационарным орбитам, где они не излучают энергию, однако, при переходе с орбиты на орбиту они могут излучать или поглощать энергию. В качестве стационарных орбит Бором приняты окружности, на которых момент количества движения, т. е. момент импульса, равен целому числу приведенных постоянных Планка. Уравнения для стационарной орбиты и энергии электрона на этой орбите: где n – номер орбиты; ћ – приведенная постоянная Планка, me – масса электрона, e – заряд электрона, Z – количество протонов в ядре, ε 0 – диэлектрическая постоянная.
 Современное описание электронного строения атомов в рамках квантовой механики • Карпускулярно-волновой дуализм, вещество обладает двойственной природой – одновременно может проявлять себя и как частица и как волна. Этот принцип описывается уравнением Луи де Бройля: где h – постоянная Планка, v – скорость электрона.
Современное описание электронного строения атомов в рамках квантовой механики • Карпускулярно-волновой дуализм, вещество обладает двойственной природой – одновременно может проявлять себя и как частица и как волна. Этот принцип описывается уравнением Луи де Бройля: где h – постоянная Планка, v – скорость электрона.
 Современное описание электронного строения атомов в рамках квантовой механики • Принцип неопределенности Гейзенберга – невозможно одновременно точно определить координаты и импульс частицы. Этот принцип описывается выражением: где Δx – погрешность при определении координаты, а Δp – погрешность при определении импульса.
Современное описание электронного строения атомов в рамках квантовой механики • Принцип неопределенности Гейзенберга – невозможно одновременно точно определить координаты и импульс частицы. Этот принцип описывается выражением: где Δx – погрешность при определении координаты, а Δp – погрешность при определении импульса.
 Современное описание электронного строения атомов в рамках квантовой механики • Уравнение Эрвина Шредингера. Движение и положение элементарной частицы в пространстве носит вероятностный характер и описывается с помощью волновой функции распределения вероятностей: где Ψ – волновая функция (пси). Полная энергия электрона состоит из кинетической и потенциальной и зависит от значения волновой функции в пространстве, т. е. носит вероятностный характер.
Современное описание электронного строения атомов в рамках квантовой механики • Уравнение Эрвина Шредингера. Движение и положение элементарной частицы в пространстве носит вероятностный характер и описывается с помощью волновой функции распределения вероятностей: где Ψ – волновая функция (пси). Полная энергия электрона состоит из кинетической и потенциальной и зависит от значения волновой функции в пространстве, т. е. носит вероятностный характер.
 Современное описание электронного строения атомов в рамках квантовой механики • Принцип запрета Паули – в одном квантовом состоянии не может находиться более одного электрона. Следствием этого принципа является наличие электронных оболочек в атоме, в результате чего наблюдается разнообразие химических элементов и их соединений. Квантовое состояние описывается четырьмя квантовыми числами: 1. n – главное квантовое число. Определяет энергию электрона (n=1, 2, 3…). 2. l – орбитальное квантовое число. Определяет форму орбитали: l=(n-1). 3. m – магнитное квантовое число. Показывает ориентацию орбит в пространстве: m=±l. 4. s – спиновое квантовое число. Характеризует вращение электрона вокруг своей оси: s=±½.
Современное описание электронного строения атомов в рамках квантовой механики • Принцип запрета Паули – в одном квантовом состоянии не может находиться более одного электрона. Следствием этого принципа является наличие электронных оболочек в атоме, в результате чего наблюдается разнообразие химических элементов и их соединений. Квантовое состояние описывается четырьмя квантовыми числами: 1. n – главное квантовое число. Определяет энергию электрона (n=1, 2, 3…). 2. l – орбитальное квантовое число. Определяет форму орбитали: l=(n-1). 3. m – магнитное квантовое число. Показывает ориентацию орбит в пространстве: m=±l. 4. s – спиновое квантовое число. Характеризует вращение электрона вокруг своей оси: s=±½.
 Теории электронного строения металлов 1. Классическая электронная теория (П. Друде и Л. Лоренц начало XX века) Валентные электроны в металле являются свободными частицами, которые могут свободно перемещаться во всех направлениях. Они являются одинаковыми твердыми сферами, двигающимися по прямым линиям до столкновения друг с другом или ионами кристаллической решетки. Под действием внешнего электрического поля возникает электрический ток: сила –e. E, направление –E.
Теории электронного строения металлов 1. Классическая электронная теория (П. Друде и Л. Лоренц начало XX века) Валентные электроны в металле являются свободными частицами, которые могут свободно перемещаться во всех направлениях. Они являются одинаковыми твердыми сферами, двигающимися по прямым линиям до столкновения друг с другом или ионами кристаллической решетки. Под действием внешнего электрического поля возникает электрический ток: сила –e. E, направление –E.
 Теории электронного строения металлов Плотность тока: , где n 0 количество электронов; e - их заряд; v - средняя скорость их упорядоченного движения, причем , где Е – приложенное напряжение, m – масса электрона, τ – время прогона электрона между двумя столкновениями. Отсюда: и проводимость: . Среднее время прогона электрона между двумя столкновениями можно представить в виде: где vтепл – скорость теплового движения электронов. Отсюда: . При комнатной температуре vтепл ~ 106 м/с, v=6*10 -4 м/с, которой можно пренебречь. Тогда где l – длинна среднего пробега электрона между двумя столкновениями. Проводимость в этом случае равна: .
Теории электронного строения металлов Плотность тока: , где n 0 количество электронов; e - их заряд; v - средняя скорость их упорядоченного движения, причем , где Е – приложенное напряжение, m – масса электрона, τ – время прогона электрона между двумя столкновениями. Отсюда: и проводимость: . Среднее время прогона электрона между двумя столкновениями можно представить в виде: где vтепл – скорость теплового движения электронов. Отсюда: . При комнатной температуре vтепл ~ 106 м/с, v=6*10 -4 м/с, которой можно пренебречь. Тогда где l – длинна среднего пробега электрона между двумя столкновениями. Проводимость в этом случае равна: .
 Теории электронного строения металлов Недостатки классической электронной теории: 1. По данным теории длина свободного пробега электрона равна 10 -8 -10 -9 2. Температурная зависимость электросопротивления, полученная в рамках теории, не соответствует экспериментальным данным: теоретически , а экспериментально. 3. Теория оказалась внутренне противоречивой, т. к. высокие тепло- и электропроводность определяются из соображения, что электроны свободные частицы для всего кристалла. А реальные значения теплоемкости можно получить на условии, что валентные электроны входят в состав атомов, т. е. не вносят вклад в теплоемкость. Электроны тоже должны вносить вклад в теплоемкость: теоретически для одновалентного металла – 4, 5 R, для двухвалентного – 6 R, а экспериментально – 3 R.
Теории электронного строения металлов Недостатки классической электронной теории: 1. По данным теории длина свободного пробега электрона равна 10 -8 -10 -9 2. Температурная зависимость электросопротивления, полученная в рамках теории, не соответствует экспериментальным данным: теоретически , а экспериментально. 3. Теория оказалась внутренне противоречивой, т. к. высокие тепло- и электропроводность определяются из соображения, что электроны свободные частицы для всего кристалла. А реальные значения теплоемкости можно получить на условии, что валентные электроны входят в состав атомов, т. е. не вносят вклад в теплоемкость. Электроны тоже должны вносить вклад в теплоемкость: теоретически для одновалентного металла – 4, 5 R, для двухвалентного – 6 R, а экспериментально – 3 R.
 Теории электронного строения металлов 2. Квантовая теория свободных электронов (А. Зоммерфельд). Теория основана на тех же экспериментальных фактах, что и классическая теория электронов. Однако состояния электронов описывается с помощью волновых функций, а распределение электронов по состояниям описывается законами квантовой статистики.
Теории электронного строения металлов 2. Квантовая теория свободных электронов (А. Зоммерфельд). Теория основана на тех же экспериментальных фактах, что и классическая теория электронов. Однако состояния электронов описывается с помощью волновых функций, а распределение электронов по состояниям описывается законами квантовой статистики.
 Теории электронного строения металлов Энергетический спектр электронов. Энергия выражается через кинетическую составляющую: . После подстановки скорости из уравнения Луи де Бройля ( ) получим: . Если в это выражение ввести волновое число , которое показывает сколько раз длина волны данного волнового процесса укладывается на отрезке длинной 2π, получим: Энергетический спектр свободной микрочастицы непрерывен и, следовательно, все кристаллы в этом случае должны быть проводниками.
Теории электронного строения металлов Энергетический спектр электронов. Энергия выражается через кинетическую составляющую: . После подстановки скорости из уравнения Луи де Бройля ( ) получим: . Если в это выражение ввести волновое число , которое показывает сколько раз длина волны данного волнового процесса укладывается на отрезке длинной 2π, получим: Энергетический спектр свободной микрочастицы непрерывен и, следовательно, все кристаллы в этом случае должны быть проводниками.
 Теории электронного строения металлов Циклические условия Борна-Кармана. Влияние размеров кристалла на состояние электронов внутри. V 0 – средняя область кристалла, минимальный объем, начиная с которого процессы внутри кристалла не зависят от явлений на поверхности. В случае соединения нескольких таких объемов, то получится объем вещества, где состояния электронов повторяются с периодичностью равному среднему размеру области V 0. волновая функция электрона в кристалле является периодической функцией с периодом, равным среднему размеру основной области.
Теории электронного строения металлов Циклические условия Борна-Кармана. Влияние размеров кристалла на состояние электронов внутри. V 0 – средняя область кристалла, минимальный объем, начиная с которого процессы внутри кристалла не зависят от явлений на поверхности. В случае соединения нескольких таких объемов, то получится объем вещества, где состояния электронов повторяются с периодичностью равному среднему размеру области V 0. волновая функция электрона в кристалле является периодической функцией с периодом, равным среднему размеру основной области.
 Теории электронного строения металлов Функция распределения Ферми – Дирака. В k-пространстве каждому энергетическому состоянию электрона соответствует значение вектора k. Поверхности с одинаковой энергией электронов в k-пространстве называются поверхностями Ферми, а максимальная энергия занятых электронами состояний называется энергией Ферми и обозначается. Вся электронная оболочка в данном случае располагается внутри сферы с радиусом k. F – сфера Ферми – что соответствует состоянию наименьшей энергии.
Теории электронного строения металлов Функция распределения Ферми – Дирака. В k-пространстве каждому энергетическому состоянию электрона соответствует значение вектора k. Поверхности с одинаковой энергией электронов в k-пространстве называются поверхностями Ферми, а максимальная энергия занятых электронами состояний называется энергией Ферми и обозначается. Вся электронная оболочка в данном случае располагается внутри сферы с радиусом k. F – сфера Ферми – что соответствует состоянию наименьшей энергии.
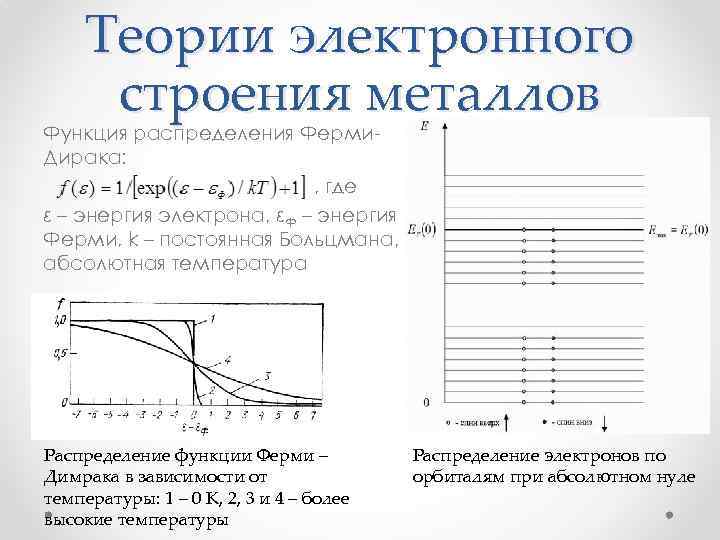 Теории электронного строения металлов Функция распределения Ферми. Дирака: , где ε – энергия электрона, εФ – энергия Ферми, k – постоянная Больцмана, T – абсолютная температура Распределение функции Ферми – Димрака в зависимости от температуры: 1 – 0 К, 2, 3 и 4 – более высокие температуры Распределение электронов по орбиталям при абсолютном нуле
Теории электронного строения металлов Функция распределения Ферми. Дирака: , где ε – энергия электрона, εФ – энергия Ферми, k – постоянная Больцмана, T – абсолютная температура Распределение функции Ферми – Димрака в зависимости от температуры: 1 – 0 К, 2, 3 и 4 – более высокие температуры Распределение электронов по орбиталям при абсолютном нуле
 Теории электронного строения металлов 3. Зонная теория почти свободных электронов. Ионы в кристаллической решетки расположены с определенной периодичностью и создают периодическое электростатическое поле, в котором и происходит движение коллективизированных электронов. Условие отражения электрона от различных плоскостей в кристаллической решетке: (уравнение Вульфа-Брегга), где - межплоскостное расстояние, - угол падения электронов на кристаллографическую плоскость, длина волны излучения, - порядок отражения (1, 2, 3…).
Теории электронного строения металлов 3. Зонная теория почти свободных электронов. Ионы в кристаллической решетки расположены с определенной периодичностью и создают периодическое электростатическое поле, в котором и происходит движение коллективизированных электронов. Условие отражения электрона от различных плоскостей в кристаллической решетке: (уравнение Вульфа-Брегга), где - межплоскостное расстояние, - угол падения электронов на кристаллографическую плоскость, длина волны излучения, - порядок отражения (1, 2, 3…).
 Теории электронного строения металлов Понятие о зонах Бриллюэна. Зоны разрешенных значений энергии при движении по кристаллической решетке, когда электроны не испытывают отражения по закону Вульфа-Брегга. Зоны Бриллюэна принято строить в k-пространстве, т. е. в воображаемом пространстве, в котором по осям откладывается значения волнового вектора График зависимости энергии электрона от волнового вектора
Теории электронного строения металлов Понятие о зонах Бриллюэна. Зоны разрешенных значений энергии при движении по кристаллической решетке, когда электроны не испытывают отражения по закону Вульфа-Брегга. Зоны Бриллюэна принято строить в k-пространстве, т. е. в воображаемом пространстве, в котором по осям откладывается значения волнового вектора График зависимости энергии электрона от волнового вектора
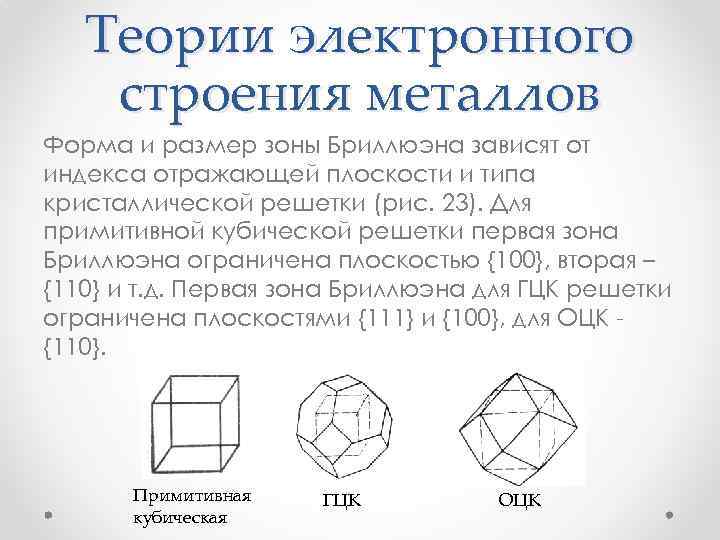 Теории электронного строения металлов Форма и размер зоны Бриллюэна зависят от индекса отражающей плоскости и типа кристаллической решетки (рис. 23). Для примитивной кубической решетки первая зона Бриллюэна ограничена плоскостью {100}, вторая – {110} и т. д. Первая зона Бриллюэна для ГЦК решетки ограничена плоскостями {111} и {100}, для ОЦК {110}. Примитивная кубическая ГЦК ОЦК
Теории электронного строения металлов Форма и размер зоны Бриллюэна зависят от индекса отражающей плоскости и типа кристаллической решетки (рис. 23). Для примитивной кубической решетки первая зона Бриллюэна ограничена плоскостью {100}, вторая – {110} и т. д. Первая зона Бриллюэна для ГЦК решетки ограничена плоскостями {111} и {100}, для ОЦК {110}. Примитивная кубическая ГЦК ОЦК
 Теории электронного строения металлов Эффективная масса электрона – масса, которая характеризует взаимодействие электрона с кристаллической решеткой и около критических значений энергии стремится к бесконечности. Кинетическая энергия электрона: , где m* - эффективная масса электрона. Проводимость в этой теории равна:
Теории электронного строения металлов Эффективная масса электрона – масса, которая характеризует взаимодействие электрона с кристаллической решеткой и около критических значений энергии стремится к бесконечности. Кинетическая энергия электрона: , где m* - эффективная масса электрона. Проводимость в этой теории равна:
 Свойства электронного газа при абсолютном нуле Предположим, что N электронов находятся в объеме v, тогда объемная плотность электронов: nэл=N/v. Частицы находятся в состоянии наименьшей энергии E=0, что противоречит принципу Паули. Состояние одной частицы с энергией Е можно характеризовать значением импульса или количеством движения р, связанного с энергией и массой частицы: ε = p 2/2 m 0 p=√ 2εm 0
Свойства электронного газа при абсолютном нуле Предположим, что N электронов находятся в объеме v, тогда объемная плотность электронов: nэл=N/v. Частицы находятся в состоянии наименьшей энергии E=0, что противоречит принципу Паули. Состояние одной частицы с энергией Е можно характеризовать значением импульса или количеством движения р, связанного с энергией и массой частицы: ε = p 2/2 m 0 p=√ 2εm 0
 Свойства электронного газа при абсолютном нуле Каждую точку пространства импульсов можно охарактеризовать радиус-вектором р, проведенным из начала координат, т. о. геометрическим местом точек, которым соответствует одно и то же значение импульса р, является сфера радиуса р. Согласно Е = p 2/2 m 0 , всем точкам этой поверхности можно приписать одно и то же значение Е. Если р0 импульс, соответствующий Е max, то объем в пространстве импульсов, внутри которого расположатся все N электронов, равен 4/3πр30. Объемом V фазового пространства называется произведение объема v обыкновенного пространства и объема 4/3πр30 в пространстве импульсов.
Свойства электронного газа при абсолютном нуле Каждую точку пространства импульсов можно охарактеризовать радиус-вектором р, проведенным из начала координат, т. о. геометрическим местом точек, которым соответствует одно и то же значение импульса р, является сфера радиуса р. Согласно Е = p 2/2 m 0 , всем точкам этой поверхности можно приписать одно и то же значение Е. Если р0 импульс, соответствующий Е max, то объем в пространстве импульсов, внутри которого расположатся все N электронов, равен 4/3πр30. Объемом V фазового пространства называется произведение объема v обыкновенного пространства и объема 4/3πр30 в пространстве импульсов.
 Свойства электронного газа при абсолютном нуле •
Свойства электронного газа при абсолютном нуле •
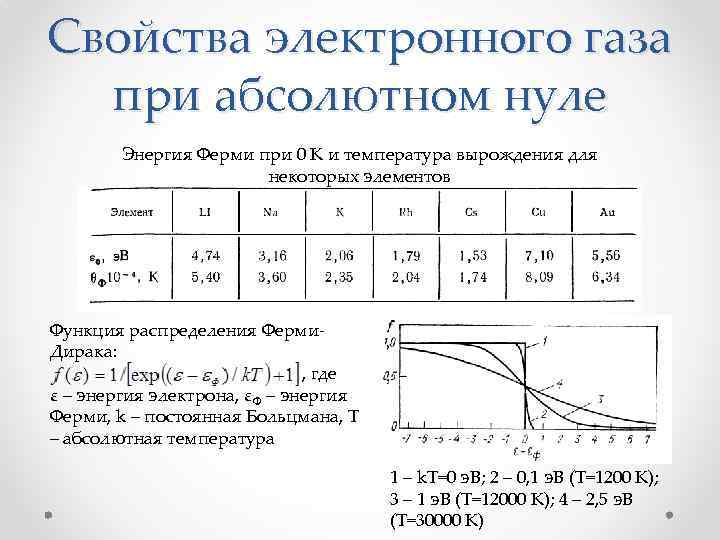 Свойства электронного газа при абсолютном нуле Энергия Ферми при 0 К и температура вырождения для некоторых элементов Функция распределения Ферми. Дирака: , где ε – энергия электрона, εФ – энергия Ферми, k – постоянная Больцмана, T – абсолютная температура 1 – k. T=0 э. В; 2 – 0, 1 э. В (Т=1200 К); 3 – 1 э. В (Т=12000 К); 4 – 2, 5 э. В (Т=30000 К)
Свойства электронного газа при абсолютном нуле Энергия Ферми при 0 К и температура вырождения для некоторых элементов Функция распределения Ферми. Дирака: , где ε – энергия электрона, εФ – энергия Ферми, k – постоянная Больцмана, T – абсолютная температура 1 – k. T=0 э. В; 2 – 0, 1 э. В (Т=1200 К); 3 – 1 э. В (Т=12000 К); 4 – 2, 5 э. В (Т=30000 К)
 Свойства электронного газа при абсолютном нуле Температуру, при которой распределение электронов по состояниям существенно изменится по сравнению с распределением при абсолютном нуле, можно определить из выражения: kθф=ε 0, откуда θф= ε 0/ k, где θф - температура вырождения электронного газа или температура Ферми, превышающая температуру плавления соответствующих металлов.
Свойства электронного газа при абсолютном нуле Температуру, при которой распределение электронов по состояниям существенно изменится по сравнению с распределением при абсолютном нуле, можно определить из выражения: kθф=ε 0, откуда θф= ε 0/ k, где θф - температура вырождения электронного газа или температура Ферми, превышающая температуру плавления соответствующих металлов.
 Свойства электронного газа при абсолютном нуле •
Свойства электронного газа при абсолютном нуле •
 Свойства электронного газа при абсолютном нуле •
Свойства электронного газа при абсолютном нуле •
 Свойства электронного газа при абсолютном нуле •
Свойства электронного газа при абсолютном нуле •
 Одноэлектронная теория •
Одноэлектронная теория •
 Одноэлектронная теория •
Одноэлектронная теория •
 Одноэлектронная теория •
Одноэлектронная теория •
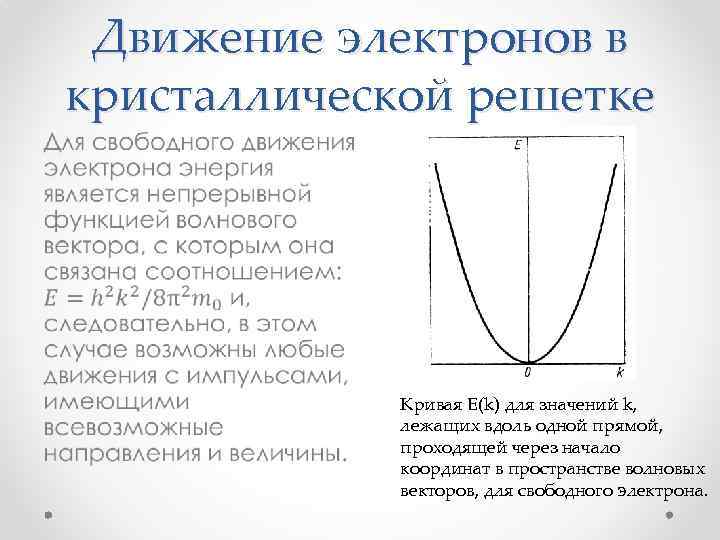 Движение электронов в кристаллической решетке • Кривая Е(k) для значений k, лежащих вдоль одной прямой, проходящей через начало координат в пространстве волновых векторов, для свободного электрона.
Движение электронов в кристаллической решетке • Кривая Е(k) для значений k, лежащих вдоль одной прямой, проходящей через начало координат в пространстве волновых векторов, для свободного электрона.
 Движение электрона в одномерной решетке •
Движение электрона в одномерной решетке •
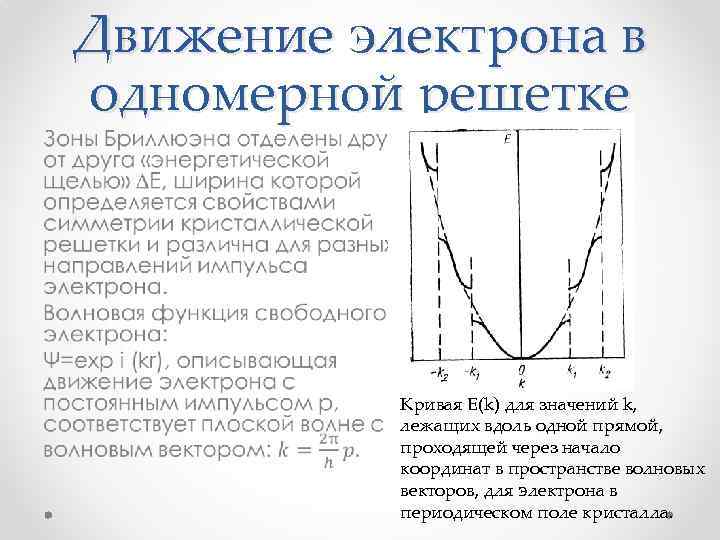 Движение электрона в одномерной решетке • Кривая Е(k) для значений k, лежащих вдоль одной прямой, проходящей через начало координат в пространстве волновых векторов, для электрона в периодическом поле кристалла.
Движение электрона в одномерной решетке • Кривая Е(k) для значений k, лежащих вдоль одной прямой, проходящей через начало координат в пространстве волновых векторов, для электрона в периодическом поле кристалла.
 Движение электронов в трехмерной решетке •
Движение электронов в трехмерной решетке •
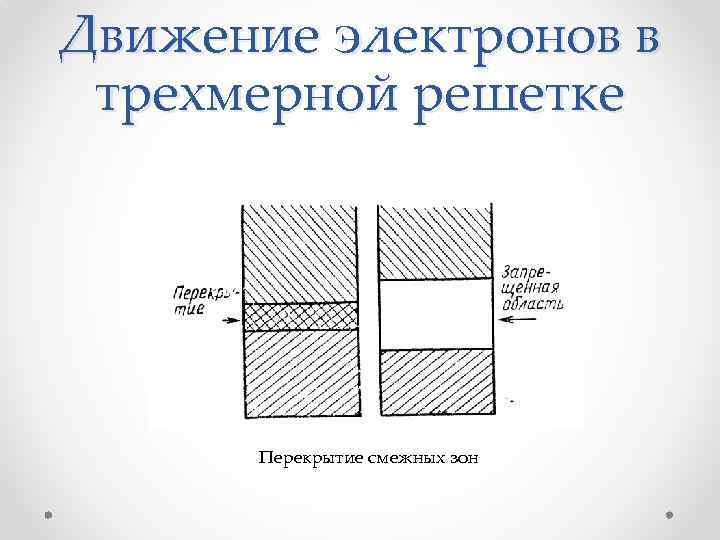 Движение электронов в трехмерной решетке Перекрытие смежных зон
Движение электронов в трехмерной решетке Перекрытие смежных зон
 Построение зон Бриллюэна •
Построение зон Бриллюэна •
 Построение зон Бриллюэна Подставляя k=2π/λ в уравнение Вульфа-Брэгга, получим: 2πn/k=2 d cos α, откуда k cos α=πn/d. k cos α=χ – проекция вектора k на нормаль к рассматриваемой плоскости и, следовательно, χ=πn/d – уравнение плоскости в пространстве волнового вектора, проходящей на расстоянии πn/d от начала координат. Зная расположение в кристалле всех отражающих плоскостей, можно построить зоны Бриллюэна, для чего необходимо воспользоваться структурным фактором интенсивности отражения электронов.
Построение зон Бриллюэна Подставляя k=2π/λ в уравнение Вульфа-Брэгга, получим: 2πn/k=2 d cos α, откуда k cos α=πn/d. k cos α=χ – проекция вектора k на нормаль к рассматриваемой плоскости и, следовательно, χ=πn/d – уравнение плоскости в пространстве волнового вектора, проходящей на расстоянии πn/d от начала координат. Зная расположение в кристалле всех отражающих плоскостей, можно построить зоны Бриллюэна, для чего необходимо воспользоваться структурным фактором интенсивности отражения электронов.
 Построение зон Бриллюэна Для кубической решетки: Из χ=πn/d следует, что наименьшему расстоянию χ соответствует наибольшее d. В кубической решетке это грани ячейки, d=a. Направляющие косинусы нормали к этим плоскостям: (+/- 1, 0, 0), (0, +/- 1, 0), (0, 0, +/-1). Первая зона – куб, ограниченный плоскостями: kx=+/- /a, ky=+/- /a, kz=+/- /a. Следующая совокупность отражающих плоскостей: d=a/√ 2, т. е. семейство {110}. Направляющие косинусы нормалей к этим плоскостям: (+/-1, 0), (+/-1, 0, +/-1), (0, +/-1). Нагруженными границами второй зоны являются плоскости: +/-kx +/ky = √ 2 /a, +/-kx +/-kz = √ 2 /a, +/-ky +/-kz= √ 2 /a,
Построение зон Бриллюэна Для кубической решетки: Из χ=πn/d следует, что наименьшему расстоянию χ соответствует наибольшее d. В кубической решетке это грани ячейки, d=a. Направляющие косинусы нормали к этим плоскостям: (+/- 1, 0, 0), (0, +/- 1, 0), (0, 0, +/-1). Первая зона – куб, ограниченный плоскостями: kx=+/- /a, ky=+/- /a, kz=+/- /a. Следующая совокупность отражающих плоскостей: d=a/√ 2, т. е. семейство {110}. Направляющие косинусы нормалей к этим плоскостям: (+/-1, 0), (+/-1, 0, +/-1), (0, +/-1). Нагруженными границами второй зоны являются плоскости: +/-kx +/ky = √ 2 /a, +/-kx +/-kz = √ 2 /a, +/-ky +/-kz= √ 2 /a,
 Построение зон Бриллюэна Для ГЦК-решетки: Первая зона образуется плоскостями, параллельными {111} и {100}. Структурный множитель отличен от 0 для отражений плоскостями {100} второго порядка (n=2). Для ОЦК-решетки: Граница первой зоны Первые зоны Бриллюэна образуется плоскостями, для гцк, оцк и гпу решеток. параллельными {100}.
Построение зон Бриллюэна Для ГЦК-решетки: Первая зона образуется плоскостями, параллельными {111} и {100}. Структурный множитель отличен от 0 для отражений плоскостями {100} второго порядка (n=2). Для ОЦК-решетки: Граница первой зоны Первые зоны Бриллюэна образуется плоскостями, для гцк, оцк и гпу решеток. параллельными {100}.
 Связь между энергетическим спектром электронов и свойствами кристаллов В первой зоне показаны кривые, соответствующие различным уровням энергии вплоть до границы зоны, во второй – только несколько наиболее низких уровней. Для самых низких уровней первой зоны форма поверхностей равных энергий не отличается от сферической. Связь между энергией электрона и волновым числом: Поверхности равных энергий в плоскости kz=0 для простой кубической решетки.
Связь между энергетическим спектром электронов и свойствами кристаллов В первой зоне показаны кривые, соответствующие различным уровням энергии вплоть до границы зоны, во второй – только несколько наиболее низких уровней. Для самых низких уровней первой зоны форма поверхностей равных энергий не отличается от сферической. Связь между энергией электрона и волновым числом: Поверхности равных энергий в плоскости kz=0 для простой кубической решетки.
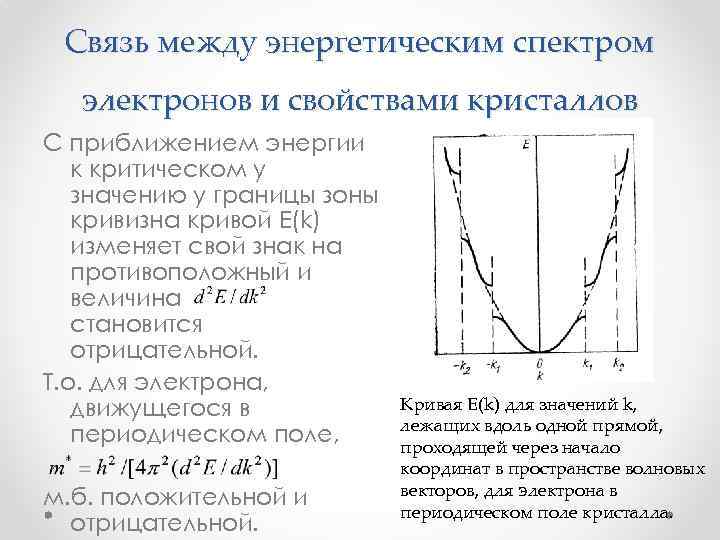 Связь между энергетическим спектром электронов и свойствами кристаллов С приближением энергии к критическом у значению у границы зоны кривизна кривой E(k) изменяет свой знак на противоположный и величина становится отрицательной. Т. о. для электрона, движущегося в периодическом поле, м. б. положительной и отрицательной. Кривая Е(k) для значений k, лежащих вдоль одной прямой, проходящей через начало координат в пространстве волновых векторов, для электрона в периодическом поле кристалла.
Связь между энергетическим спектром электронов и свойствами кристаллов С приближением энергии к критическом у значению у границы зоны кривизна кривой E(k) изменяет свой знак на противоположный и величина становится отрицательной. Т. о. для электрона, движущегося в периодическом поле, м. б. положительной и отрицательной. Кривая Е(k) для значений k, лежащих вдоль одной прямой, проходящей через начало координат в пространстве волновых векторов, для электрона в периодическом поле кристалла.
 Связь между энергетическим спектром электронов и свойствами кристаллов Эффективная масса может зависеть от направления движения электрона и характеризует его взаимодействие с кристаллической решеткой. У свободного электрона. Назовем в этом случае кристалл идеальным металлом. Отклонение реального от идеального характеризуется: для электронов проводимости. У щелочных металлов: 0, 653; 1, 069; 1, 72. У натрия массы наиболее близки.
Связь между энергетическим спектром электронов и свойствами кристаллов Эффективная масса может зависеть от направления движения электрона и характеризует его взаимодействие с кристаллической решеткой. У свободного электрона. Назовем в этом случае кристалл идеальным металлом. Отклонение реального от идеального характеризуется: для электронов проводимости. У щелочных металлов: 0, 653; 1, 069; 1, 72. У натрия массы наиболее близки.
 Связь между энергетическим спектром электронов и свойствами кристаллов Для пониманию свойств кристаллов необходимо знать величину n(ε)dε, представляющую собой число электронов в единице объема, энергии которых лежат в интервале ε и ε+dε. Выражая энергию через волновое число, получаем: Элемент объема в пространстве волнового вектора: и следовательно: , при интегрировании которого по объему куба с ребром 2 /а, в правой части получим: . В левой – число электронов в 1 см 3 металла.
Связь между энергетическим спектром электронов и свойствами кристаллов Для пониманию свойств кристаллов необходимо знать величину n(ε)dε, представляющую собой число электронов в единице объема, энергии которых лежат в интервале ε и ε+dε. Выражая энергию через волновое число, получаем: Элемент объема в пространстве волнового вектора: и следовательно: , при интегрировании которого по объему куба с ребром 2 /а, в правой части получим: . В левой – число электронов в 1 см 3 металла.
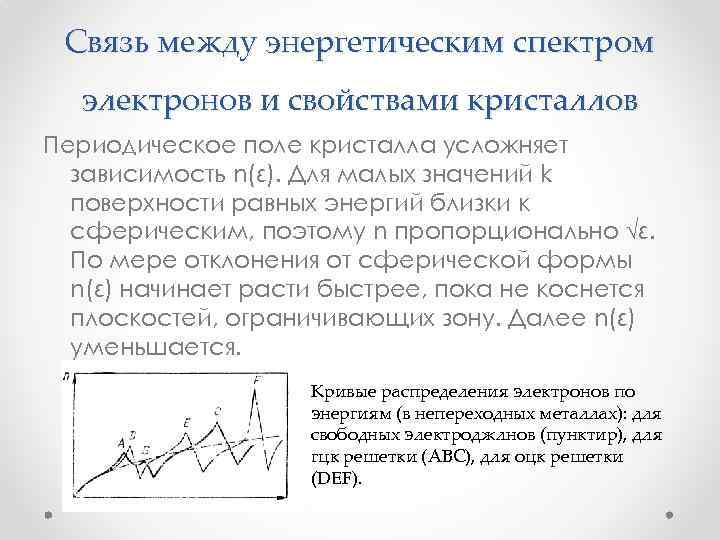 Связь между энергетическим спектром электронов и свойствами кристаллов Периодическое поле кристалла усложняет зависимость n(ε). Для малых значений k поверхности равных энергий близки к сферическим, поэтому n пропорционально √ε. По мере отклонения от сферической формы n(ε) начинает расти быстрее, пока не коснется плоскостей, ограничивающих зону. Далее n(ε) уменьшается. Кривые распределения электронов по энергиям (в непереходных металлах): для свободных электроджлнов (пунктир), для гцк решетки (ABC), для оцк решетки (DEF).
Связь между энергетическим спектром электронов и свойствами кристаллов Периодическое поле кристалла усложняет зависимость n(ε). Для малых значений k поверхности равных энергий близки к сферическим, поэтому n пропорционально √ε. По мере отклонения от сферической формы n(ε) начинает расти быстрее, пока не коснется плоскостей, ограничивающих зону. Далее n(ε) уменьшается. Кривые распределения электронов по энергиям (в непереходных металлах): для свободных электроджлнов (пунктир), для гцк решетки (ABC), для оцк решетки (DEF).
 Связь между энергетическим спектром электронов и свойствами кристаллов Энергия электронного газа в решетке должна быть минимальной, электроны стремятся разместиться в пределах первой зоны. В двух веществах с различной электронной концентрацией: На поверхностях Ферми, касающейся границы первой зоны, значение энергии: Здесь рпред = h/2 d – длина перпендикуляра, опущенного в пространстве импульсов из начала координат на плоскость, ограничивающую зону.
Связь между энергетическим спектром электронов и свойствами кристаллов Энергия электронного газа в решетке должна быть минимальной, электроны стремятся разместиться в пределах первой зоны. В двух веществах с различной электронной концентрацией: На поверхностях Ферми, касающейся границы первой зоны, значение энергии: Здесь рпред = h/2 d – длина перпендикуляра, опущенного в пространстве импульсов из начала координат на плоскость, ограничивающую зону.
 Связь между энергетическим спектром электронов и свойствами кристаллов Для гцк решетки d 111=a√ 3. Период гцк решетки а связан с числом атомов Nат в объеме v соотношением Nат /v=4/a 3. Следовательно: При комбинировании с Получаем: где Nэл – число валентных электронов в объеме v. Сравнив соотношения, получим: или
Связь между энергетическим спектром электронов и свойствами кристаллов Для гцк решетки d 111=a√ 3. Период гцк решетки а связан с числом атомов Nат в объеме v соотношением Nат /v=4/a 3. Следовательно: При комбинировании с Получаем: где Nэл – число валентных электронов в объеме v. Сравнив соотношения, получим: или
 Связь между энергетическим спектром электронов и свойствами кристаллов Найдем общее выражение для расчета электронной концентрации сэл , при которой поверхность Ферми касается границ првой зоны Бриллюэна. В случае кубического кристалла расстояние между атомными плоскостями: Если число атомов на элементарную ячейку nат, то для кубического кристалла с периодом а Nат/v=nат/а 3. Тогда формула для рпред принимает вид:
Связь между энергетическим спектром электронов и свойствами кристаллов Найдем общее выражение для расчета электронной концентрации сэл , при которой поверхность Ферми касается границ првой зоны Бриллюэна. В случае кубического кристалла расстояние между атомными плоскостями: Если число атомов на элементарную ячейку nат, то для кубического кристалла с периодом а Nат/v=nат/а 3. Тогда формула для рпред принимает вид:
 Связь между энергетическим спектром электронов и свойствами кристаллов Из и Получим: Для оцк решетки Сэл=1, 48. Для сплавов (Сu – 50 % Zn): ½*1+1/2*2=3/2
Связь между энергетическим спектром электронов и свойствами кристаллов Из и Получим: Для оцк решетки Сэл=1, 48. Для сплавов (Сu – 50 % Zn): ½*1+1/2*2=3/2
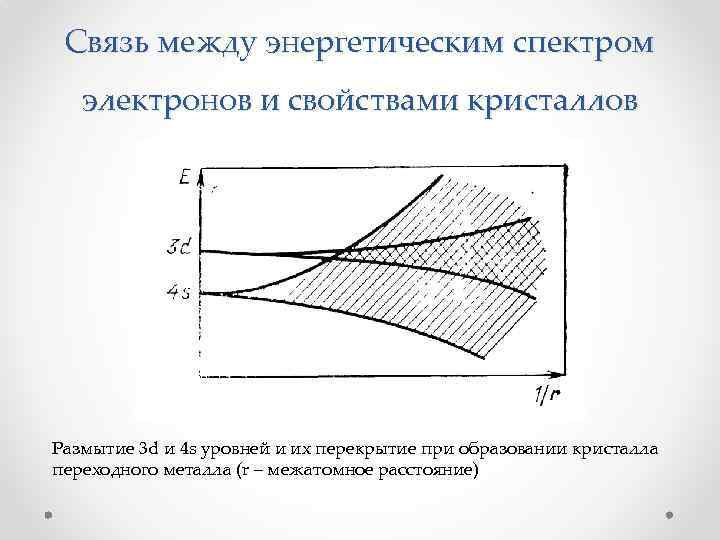 Связь между энергетическим спектром электронов и свойствами кристаллов Размытие 3 d и 4 s уровней и их перекрытие при образовании кристалла переходного металла (r – межатомное расстояние)
Связь между энергетическим спектром электронов и свойствами кристаллов Размытие 3 d и 4 s уровней и их перекрытие при образовании кристалла переходного металла (r – межатомное расстояние)
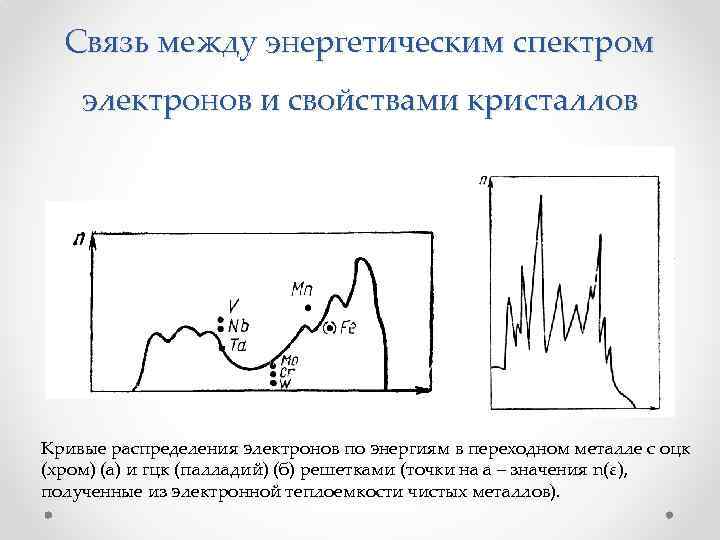 Связь между энергетическим спектром электронов и свойствами кристаллов Кривые распределения электронов по энергиям в переходном металле с оцк (хром) (а) и гцк (палладий) (б) решетками (точки на а – значения n(ε), полученные из электронной теплоемкости чистых металлов).
Связь между энергетическим спектром электронов и свойствами кристаллов Кривые распределения электронов по энергиям в переходном металле с оцк (хром) (а) и гцк (палладий) (б) решетками (точки на а – значения n(ε), полученные из электронной теплоемкости чистых металлов).
 Кристаллическая структура химических элементов
Кристаллическая структура химических элементов
 Координационные числа • Для элементов IV-VII групп (неметаллов и полуметаллических элементов): координационные числа равны валентности соответствующих элементов по водороду z=8 -p, где р – число валентных электронов атома, равное номеру группы периодической системы. Это правило показывает, что в кристаллах таких элементов основная – ковалентная связь, осуществляемая парами электронов, одновременно принадлежащим 2 соседним атомам. Каждый атом стремится иметь максимальное число соседей, отдавая для связи 1 из своих неспаренных электронов.
Координационные числа • Для элементов IV-VII групп (неметаллов и полуметаллических элементов): координационные числа равны валентности соответствующих элементов по водороду z=8 -p, где р – число валентных электронов атома, равное номеру группы периодической системы. Это правило показывает, что в кристаллах таких элементов основная – ковалентная связь, осуществляемая парами электронов, одновременно принадлежащим 2 соседним атомам. Каждый атом стремится иметь максимальное число соседей, отдавая для связи 1 из своих неспаренных электронов.
 Распределение валентных электронов Изолированный атом углерода Кристаллическая структура алмаза Кристаллическая структура графита
Распределение валентных электронов Изолированный атом углерода Кристаллическая структура алмаза Кристаллическая структура графита
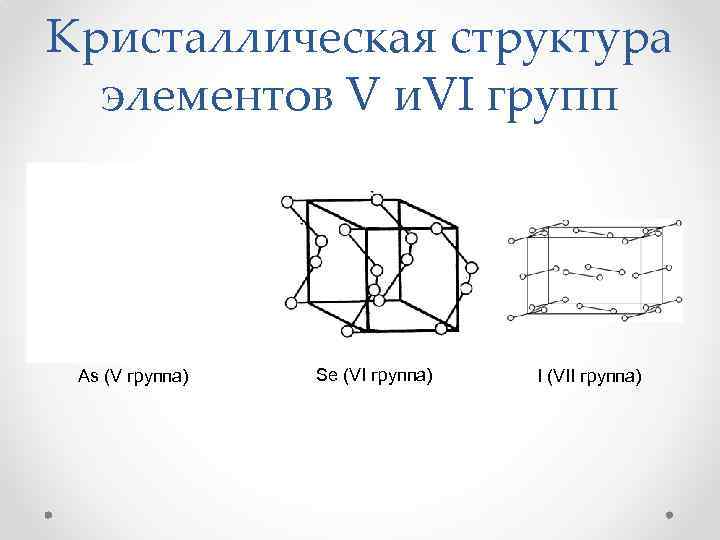 Кристаллическая структура элементов V и. VI групп As (V группа) Se (VI группа) I (VII группа)
Кристаллическая структура элементов V и. VI групп As (V группа) Se (VI группа) I (VII группа)
 Степень компактности некоторых структур Тип решетки Координационно е число Коэффициент заполнения кристалла атомами Объем межатомных промежутков, % общего объема кристалла ГПУ 12 0, 74 26 ГЦК 12 0, 74 26 ОЦК 8 0, 68 32 Простая кубическая 6 0, 52 48 Алмаз 4 0, 34 66 Теллур 2 0, 23 77
Степень компактности некоторых структур Тип решетки Координационно е число Коэффициент заполнения кристалла атомами Объем межатомных промежутков, % общего объема кристалла ГПУ 12 0, 74 26 ГЦК 12 0, 74 26 ОЦК 8 0, 68 32 Простая кубическая 6 0, 52 48 Алмаз 4 0, 34 66 Теллур 2 0, 23 77
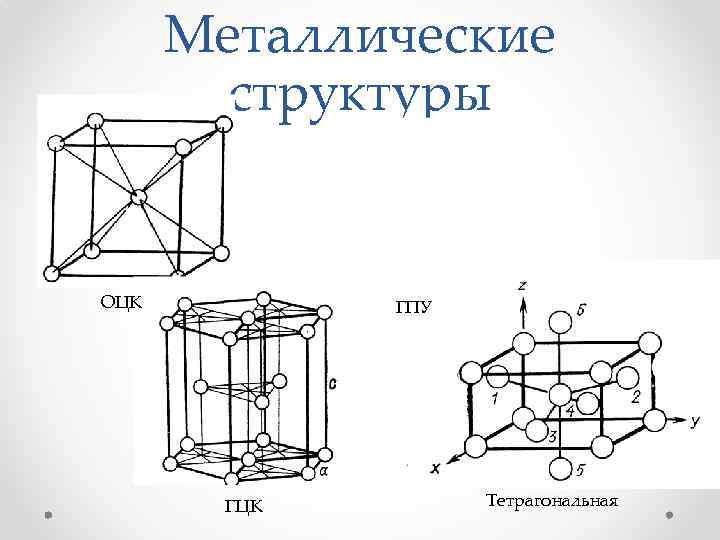 Металлические структуры ОЦК ГПУ ГЦК Тетрагональная
Металлические структуры ОЦК ГПУ ГЦК Тетрагональная
 Периодический закон в кристаллическом строении • Щелочные металлы: ОЦК • Металлы подгруппы меди (Cu, Ag, Au): ГЦК • Металлы II группы с достроенными внутренними оболочками (Ве, Mg, Zn, Cd): ГПУ • Hg: простая ромбоэдрическая решетка • Металлы II группы с недостроенной d-оболочкой (Ca, Sr) – ГЦК, но кальций при 450 С и выше имеет ГПУ, а в присутствии некоторых примесей – ОЦК • Специфические решетки у металлов III группы: Ga, In, β-Sn – тетрагональная решетка; Mn – помимо ОЦК решетки твердых растворов и электронных соединений. • Актиноиды: β-U – тетрагональная с 30 атомами на элементарную ячейку.
Периодический закон в кристаллическом строении • Щелочные металлы: ОЦК • Металлы подгруппы меди (Cu, Ag, Au): ГЦК • Металлы II группы с достроенными внутренними оболочками (Ве, Mg, Zn, Cd): ГПУ • Hg: простая ромбоэдрическая решетка • Металлы II группы с недостроенной d-оболочкой (Ca, Sr) – ГЦК, но кальций при 450 С и выше имеет ГПУ, а в присутствии некоторых примесей – ОЦК • Специфические решетки у металлов III группы: Ga, In, β-Sn – тетрагональная решетка; Mn – помимо ОЦК решетки твердых растворов и электронных соединений. • Актиноиды: β-U – тетрагональная с 30 атомами на элементарную ячейку.
 Полиморфные превращения • У большинства металлов ОЦК – высокотемпературная модификация. • Температура полиморфного превращения зависит от примесей и давления: • Принцип ле Шателье: высокое давление снижает температуру перехода, когда низкотемпературная модификация менее компактна, чем высокотемпературная и повышает в противоположном случае.
Полиморфные превращения • У большинства металлов ОЦК – высокотемпературная модификация. • Температура полиморфного превращения зависит от примесей и давления: • Принцип ле Шателье: высокое давление снижает температуру перехода, когда низкотемпературная модификация менее компактна, чем высокотемпературная и повышает в противоположном случае.
 Переходные металлы • Металлы IA подгруппы (Cu, Ag, Au) в некоторых случаях ведут себя как переходные. • Переходные металлы разбиваются на несколько групп: o I группа (3 d металлы): с Sc до Ni. o II группа (3 d металлы): с Y до Pd. Особая переходная группа – редкоземельные (4 f металлы) от Се до Lu o III группа (5 d) от Hf до Pt. Ac (89 элемент)начинает ряд актиноидов (6 d). Th и последующие элементы – заполняется 5 f оболочка.
Переходные металлы • Металлы IA подгруппы (Cu, Ag, Au) в некоторых случаях ведут себя как переходные. • Переходные металлы разбиваются на несколько групп: o I группа (3 d металлы): с Sc до Ni. o II группа (3 d металлы): с Y до Pd. Особая переходная группа – редкоземельные (4 f металлы) от Се до Lu o III группа (5 d) от Hf до Pt. Ac (89 элемент)начинает ряд актиноидов (6 d). Th и последующие элементы – заполняется 5 f оболочка.
 Характеристики металла и его атомный номер • Определенная кристаллическая структура соответствует примерно одинаковому числу s+d электронов на 1 атом, т. е области образования определенных структур расположены почти вертикально. • Чем больше электронов принимает участие в связи, тем сильнее взаимодействие атомов в решетке. • Для нормальных металлов: в пределах группы при увеличении атомного номера прочность связи снижается, в переходной группе четкой картины нет. В V группе все характеристики растут с увеличением атомного номера.
Характеристики металла и его атомный номер • Определенная кристаллическая структура соответствует примерно одинаковому числу s+d электронов на 1 атом, т. е области образования определенных структур расположены почти вертикально. • Чем больше электронов принимает участие в связи, тем сильнее взаимодействие атомов в решетке. • Для нормальных металлов: в пределах группы при увеличении атомного номера прочность связи снижается, в переходной группе четкой картины нет. В V группе все характеристики растут с увеличением атомного номера.
 Строение расплавленных металлов и кристаллизация
Строение расплавленных металлов и кристаллизация
 Строение жидких металлов • Строение жидкости оказывает существенное влияние на структуру и свойства твердого тела после кристаллизации. • По своему строение жидкости ближе к твердым телам, чем к газам. Между частицами жидкости существует довольно сильное взаимодействие, при этом атомы не упорядочены. • При плавлении объем металла изменяется на 2 – 6 %, т. е. межатомное расстояние меняется слабо. • Смещение в процессе течения одних частиц относительно других происходит так, что каждая частица остается окруженной такими же соседними частицами, и среднее расстояние между ними не меняется, хотя на место одних частиц приходя другие.
Строение жидких металлов • Строение жидкости оказывает существенное влияние на структуру и свойства твердого тела после кристаллизации. • По своему строение жидкости ближе к твердым телам, чем к газам. Между частицами жидкости существует довольно сильное взаимодействие, при этом атомы не упорядочены. • При плавлении объем металла изменяется на 2 – 6 %, т. е. межатомное расстояние меняется слабо. • Смещение в процессе течения одних частиц относительно других происходит так, что каждая частица остается окруженной такими же соседними частицами, и среднее расстояние между ними не меняется, хотя на место одних частиц приходя другие.
 Сжимаемость В области упругих деформаций изменение d. V объема V вещества пропорционально величине этого исходного объема и изменению dp внешнего давления: d. V = βVdp Или d. V/V = βdp, β = 1/V (d. V/dp). У жидких металлов значения сжимаемости низкие, что свидетельствует о малом межатомном расстоянии и сильном взаимодействии.
Сжимаемость В области упругих деформаций изменение d. V объема V вещества пропорционально величине этого исходного объема и изменению dp внешнего давления: d. V = βVdp Или d. V/V = βdp, β = 1/V (d. V/dp). У жидких металлов значения сжимаемости низкие, что свидетельствует о малом межатомном расстоянии и сильном взаимодействии.
 Свойства жидких металлов • Теплота плавления на 5 -10 % превышает теплоту испарения, это свидетельствует о том, что энергия связи при плавлении изменяется всего на несколько %. • Электросопротивление жидкости на 50 -75 % больше, что является несущественным изменением. • Теплопроводность жидкости на 50 -75 % ниже.
Свойства жидких металлов • Теплота плавления на 5 -10 % превышает теплоту испарения, это свидетельствует о том, что энергия связи при плавлении изменяется всего на несколько %. • Электросопротивление жидкости на 50 -75 % больше, что является несущественным изменением. • Теплопроводность жидкости на 50 -75 % ниже.
 Свойства жидких металлов • Электропроводности металлов обусловлена коллективизироваными электронами, электросопротивление – взаимодействием электронов с тепловыми колебаниями атомов решетки. Чем выше Т, тем выше R. То же самое характерно для жидкого состояния, исключение двухвалентные металлы. • Отражательная способность жидких металлов мало отличается от этой характеристики кристаллов.
Свойства жидких металлов • Электропроводности металлов обусловлена коллективизироваными электронами, электросопротивление – взаимодействием электронов с тепловыми колебаниями атомов решетки. Чем выше Т, тем выше R. То же самое характерно для жидкого состояния, исключение двухвалентные металлы. • Отражательная способность жидких металлов мало отличается от этой характеристики кристаллов.
 Ближний и дальний порядок Т. о. отличия жидкости от кристаллов незначительны, однако металлы приобретают специфические свойства жидкости, что объясняется существованием ближнего и дальнего порядка. Отсутствие порядка в расположении частиц означает, что нет никакой закономерности в их взаимном расположении и положение одной частицы не зависит от положения остальных (идеальный газ). Ближним порядком называется наличие закономерности в расположении атомов относительно друга на расстояниях, сравнимых с межатомными. Дальним порядком называется упорядоченность на расстояниях, сравнимых с линейными размерами системы.
Ближний и дальний порядок Т. о. отличия жидкости от кристаллов незначительны, однако металлы приобретают специфические свойства жидкости, что объясняется существованием ближнего и дальнего порядка. Отсутствие порядка в расположении частиц означает, что нет никакой закономерности в их взаимном расположении и положение одной частицы не зависит от положения остальных (идеальный газ). Ближним порядком называется наличие закономерности в расположении атомов относительно друга на расстояниях, сравнимых с межатомными. Дальним порядком называется упорядоченность на расстояниях, сравнимых с линейными размерами системы.
 Положение равновесия В структуре жидкости отсутствует дальни порядок, но имеется ближний. Т. О. для каждого атома можно ввести понятие положения равновесия, т. е. определенного места в пространстве, относительно которого в среднем в течение определенного времени сохраняют свои позиции окружающие атомы. Каждый атом колеблется вокруг положения временного равновесия и далее перемещается в новое положение равновесия на расстояние атомного диаметра. Перемещение возможно в нескольких направлениях, центры атомов лежат в пределах координационной сферы. Время колебания составляет 10 -6 при Т=10 3.
Положение равновесия В структуре жидкости отсутствует дальни порядок, но имеется ближний. Т. О. для каждого атома можно ввести понятие положения равновесия, т. е. определенного места в пространстве, относительно которого в среднем в течение определенного времени сохраняют свои позиции окружающие атомы. Каждый атом колеблется вокруг положения временного равновесия и далее перемещается в новое положение равновесия на расстояние атомного диаметра. Перемещение возможно в нескольких направлениях, центры атомов лежат в пределах координационной сферы. Время колебания составляет 10 -6 при Т=10 3.
 Функция радиального распределения Функция – количественная характеристика порядка. d. W (r) – вероятность обнаружить атом на рсстоянии от r до r+dr от центра какого-либо фиксированного атома; V – объем системы; n – число частиц в единице объема. Экспериментально функцию можно определить рентгеновским методом.
Функция радиального распределения Функция – количественная характеристика порядка. d. W (r) – вероятность обнаружить атом на рсстоянии от r до r+dr от центра какого-либо фиксированного атома; V – объем системы; n – число частиц в единице объема. Экспериментально функцию можно определить рентгеновским методом.
 Основные выводы • Металл – конденсированная система, в которой атомы находятся на расстояниях, близких к межатомным в кристалле. • В пространственном расположении атомов существует ближний порядок. • Межатомное взаимодействие осуществляется коллективизированными электронами. • В расплавах сохраняются характерные признаки металлического состояния.
Основные выводы • Металл – конденсированная система, в которой атомы находятся на расстояниях, близких к межатомным в кристалле. • В пространственном расположении атомов существует ближний порядок. • Межатомное взаимодействие осуществляется коллективизированными электронами. • В расплавах сохраняются характерные признаки металлического состояния.
 Кристаллизация металлов Кристаллизация - это переход из системы атомов из термодинамически неустойчивого при данных внешних условиях состояния в устойчивое кристаллическое состояние. 2 основных этапа: - Зарождение центров кристаллической фазы; - Их рост. Критический размер зародыша – средний минимальный размер объема кристаллической фазы, начиная с которого дальнейшее увеличение этого объема приводит к прогрессирующему энергетическому выигрышу. Скорость зарождение кристаллов зависит от подвижности атомов в жидкости. Скорость выше при образовании зародыша на подложке. Т. о. кристаллическая структура в твердом состоянии определяется условиями его затвердевания.
Кристаллизация металлов Кристаллизация - это переход из системы атомов из термодинамически неустойчивого при данных внешних условиях состояния в устойчивое кристаллическое состояние. 2 основных этапа: - Зарождение центров кристаллической фазы; - Их рост. Критический размер зародыша – средний минимальный размер объема кристаллической фазы, начиная с которого дальнейшее увеличение этого объема приводит к прогрессирующему энергетическому выигрышу. Скорость зарождение кристаллов зависит от подвижности атомов в жидкости. Скорость выше при образовании зародыша на подложке. Т. о. кристаллическая структура в твердом состоянии определяется условиями его затвердевания.
 Дислокации
Дислокации
 Прочность идеальных и реальных кристаллов •
Прочность идеальных и реальных кристаллов •
 Прочность идеальных и реальных кристаллов •
Прочность идеальных и реальных кристаллов •
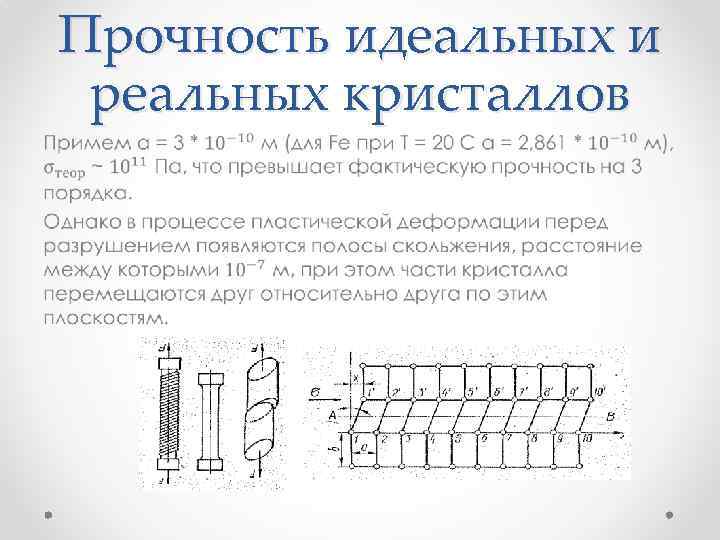 Прочность идеальных и реальных кристаллов •
Прочность идеальных и реальных кристаллов •
 Прочность идеальных и реальных кристаллов •
Прочность идеальных и реальных кристаллов •
 Прочность идеальных и реальных кристаллов •
Прочность идеальных и реальных кристаллов •
 Прочность идеальных и реальных кристаллов •
Прочность идеальных и реальных кристаллов •
 Дефекты в кристаллах •
Дефекты в кристаллах •
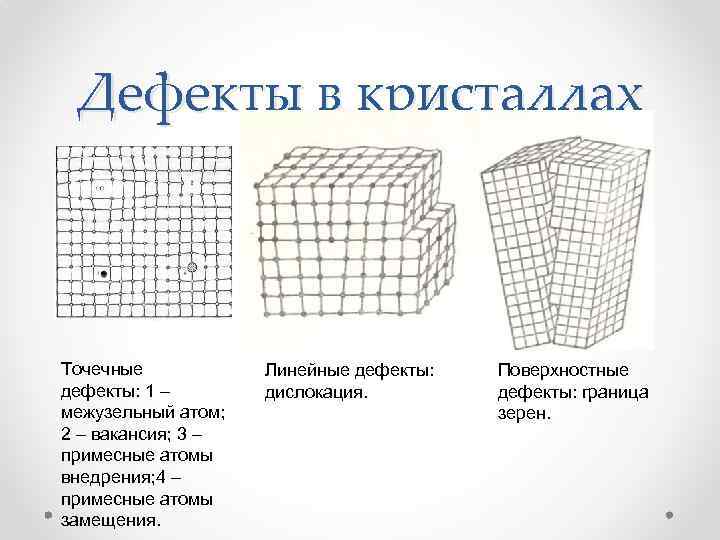 Дефекты в кристаллах Точечные дефекты: 1 – межузельный атом; 2 – вакансия; 3 – примесные атомы внедрения; 4 – примесные атомы замещения. Линейные дефекты: дислокация. Поверхностные дефекты: граница зерен.
Дефекты в кристаллах Точечные дефекты: 1 – межузельный атом; 2 – вакансия; 3 – примесные атомы внедрения; 4 – примесные атомы замещения. Линейные дефекты: дислокация. Поверхностные дефекты: граница зерен.
 Дефекты в кристаллах • Краевая дислокация – линейный дефект, возникающий в окрестности края атомной плоскости, которая обрывается внутри кристалла. Эту плоскость называют полуплоскостью или экстраплоскостью. Обозначается ┴.
Дефекты в кристаллах • Краевая дислокация – линейный дефект, возникающий в окрестности края атомной плоскости, которая обрывается внутри кристалла. Эту плоскость называют полуплоскостью или экстраплоскостью. Обозначается ┴.
 Дефекты в кристаллах •
Дефекты в кристаллах •
 Дефекты в кристаллах Линия дислокации – это ось области плохого материала, т. е. это геометрическая линия, она не проходит через атомы. Однако часто понятия дислокации и линии дислокации отождествляют. Протяженность экстраплоскости, EF.
Дефекты в кристаллах Линия дислокации – это ось области плохого материала, т. е. это геометрическая линия, она не проходит через атомы. Однако часто понятия дислокации и линии дислокации отождествляют. Протяженность экстраплоскости, EF.
 Дефекты в кристаллах Движение краевой дислокации приводит к сдвигу одной части кристалла относительно другой.
Дефекты в кристаллах Движение краевой дислокации приводит к сдвигу одной части кристалла относительно другой.
 Дефекты в кристаллах • Если в реальном кристалле уже присутствуют дислокации, то напряжение, необходимое для реализации пластической деформации, снижается. • При наличии дислокации импульс внешних сил передается от атома к атому последовательно. • Смещение атома равно 1 межатомному расстоянию. • Перемещение краевой дислокации по плоскости скольжения – это перемещение определенного размещения атомов.
Дефекты в кристаллах • Если в реальном кристалле уже присутствуют дислокации, то напряжение, необходимое для реализации пластической деформации, снижается. • При наличии дислокации импульс внешних сил передается от атома к атому последовательно. • Смещение атома равно 1 межатомному расстоянию. • Перемещение краевой дислокации по плоскости скольжения – это перемещение определенного размещения атомов.
 Дефекты в кристаллах Дислокация всегда отделяет ту часть плоскости, где сдвиг прошел, от той части плоскости, где сдвиг еще не произошел. При этом в области плохого материала сдвиг начался, но еще не закончился. Случай б – дислокация перестает существовать.
Дефекты в кристаллах Дислокация всегда отделяет ту часть плоскости, где сдвиг прошел, от той части плоскости, где сдвиг еще не произошел. При этом в области плохого материала сдвиг начался, но еще не закончился. Случай б – дислокация перестает существовать.
 Дефекты в кристаллах Фрагмент движения отрицательной дислокации. Отрицательная краевая дислокация движется в плоскости против приложенного напряжения. Аннигиляция дислокаций – встреча и взаимное уничтожение дислокаций противоположных знаков.
Дефекты в кристаллах Фрагмент движения отрицательной дислокации. Отрицательная краевая дислокация движется в плоскости против приложенного напряжения. Аннигиляция дислокаций – встреча и взаимное уничтожение дислокаций противоположных знаков.
 Дефекты в кристаллах • Винтовая дислокация. По аналогии с краевой, конфигурация атомов в области искаженного материала вокруг EF обладает повышенной подвижностью и под действием касательных напряжений, имеющих направление A->D, атомы будут смещаться в этом направлении, а линия EF – ось области «плохого материала» - в направлении D->C (A->B). EF движется в перпендикулярном к напряжению направлении.
Дефекты в кристаллах • Винтовая дислокация. По аналогии с краевой, конфигурация атомов в области искаженного материала вокруг EF обладает повышенной подвижностью и под действием касательных напряжений, имеющих направление A->D, атомы будут смещаться в этом направлении, а линия EF – ось области «плохого материала» - в направлении D->C (A->B). EF движется в перпендикулярном к напряжению направлении.
 Дефекты в кристаллах Пространственное расположение атомов вокруг линии EF:
Дефекты в кристаллах Пространственное расположение атомов вокруг линии EF:
 Дефекты в кристаллах Краевая и винтовая – важнейшие виды дислокаций, что вытекает из соображений: • Поскольку винтовая «+» движется в направлении приложенного напряжения, а винтовая – в перпендикулярном направлении, то можно ожидать, что промежуточные случаи можно представить как суперпозицию движений определенного набора краевых и винтовых дислокаций. • Винтовые и краевые дислокации образуются при кристаллизации, в процессе пластической деформации и т. п.
Дефекты в кристаллах Краевая и винтовая – важнейшие виды дислокаций, что вытекает из соображений: • Поскольку винтовая «+» движется в направлении приложенного напряжения, а винтовая – в перпендикулярном направлении, то можно ожидать, что промежуточные случаи можно представить как суперпозицию движений определенного набора краевых и винтовых дислокаций. • Винтовые и краевые дислокации образуются при кристаллизации, в процессе пластической деформации и т. п.
 Математический способ описания дислокаций Под количественным описанием физической системы понимается ее описание с помощью набора параметров, каждый из которых принимает в определенном физическом состоянии определенное числовое значение. Для полного количественного описания дислокации необходимо описать смещение из равновесных состояний всех атомов кристалла, в котором она образовалась. Для области «хорошего» материала используют теорию упругости, для ядра дислокации: Описание кристалла, содержащего дислокации + Описание всего объема кристалла, за исключением областей плохого материала методом теории упругости + Те сведения о ядрах дислокаций, которые можно получить, не зная их структуры
Математический способ описания дислокаций Под количественным описанием физической системы понимается ее описание с помощью набора параметров, каждый из которых принимает в определенном физическом состоянии определенное числовое значение. Для полного количественного описания дислокации необходимо описать смещение из равновесных состояний всех атомов кристалла, в котором она образовалась. Для области «хорошего» материала используют теорию упругости, для ядра дислокации: Описание кристалла, содержащего дислокации + Описание всего объема кристалла, за исключением областей плохого материала методом теории упругости + Те сведения о ядрах дислокаций, которые можно получить, не зная их структуры
 Математический способ описания дислокаций •
Математический способ описания дислокаций •
 Математический способ описания дислокаций • Для краевой дислокации: необходимо провести суммирование атомных смещений вдоль плоского контура. • Для винтовой дислокации: необходимо выбрать пространственный контур такого типа, повторением которого в пространстве можно получить всю поверхность, охватывающую линию дислокации. Контур интегрирования необходимо выбирать так, чтобы он располагался на большом расстоянии от линии дислокации (только в «хорошем» материале).
Математический способ описания дислокаций • Для краевой дислокации: необходимо провести суммирование атомных смещений вдоль плоского контура. • Для винтовой дислокации: необходимо выбрать пространственный контур такого типа, повторением которого в пространстве можно получить всю поверхность, охватывающую линию дислокации. Контур интегрирования необходимо выбирать так, чтобы он располагался на большом расстоянии от линии дислокации (только в «хорошем» материале).
 Математический способ описания дислокаций • Упрощенная схема краевой дислокации
Математический способ описания дислокаций • Упрощенная схема краевой дислокации
 Математический способ описания дислокаций •
Математический способ описания дислокаций •
 Математический способ описания дислокаций •
Математический способ описания дислокаций •
 Математический способ описания дислокаций •
Математический способ описания дислокаций •
 Математический способ описания дислокаций •
Математический способ описания дислокаций •
 Математический способ описания дислокаций •
Математический способ описания дислокаций •
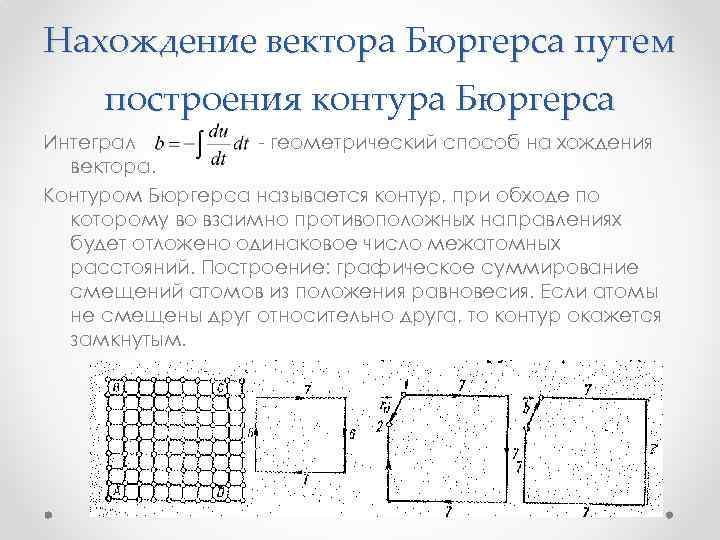 Нахождение вектора Бюргерса путем построения контура Бюргерса Интеграл - геометрический способ на хождения вектора. Контуром Бюргерса называется контур, при обходе по которому во взаимно противоположных направлениях будет отложено одинаковое число межатомных расстояний. Построение: графическое суммирование смещений атомов из положения равновесия. Если атомы не смещены друг относительно друга, то контур окажется замкнутым.
Нахождение вектора Бюргерса путем построения контура Бюргерса Интеграл - геометрический способ на хождения вектора. Контуром Бюргерса называется контур, при обходе по которому во взаимно противоположных направлениях будет отложено одинаковое число межатомных расстояний. Построение: графическое суммирование смещений атомов из положения равновесия. Если атомы не смещены друг относительно друга, то контур окажется замкнутым.
 Нахождение вектора Бюргерса путем построения контура Бюргерса Если контур незамкнут, то сумма упругих смещений атомов равна вектору, который соединяет начало контура с его концом: Поскольку, по определению, вектор Бюргерса: то вектор Бюргерса находится графически как вектор, соединяющий конец контура Бюргерса с его началом.
Нахождение вектора Бюргерса путем построения контура Бюргерса Если контур незамкнут, то сумма упругих смещений атомов равна вектору, который соединяет начало контура с его концом: Поскольку, по определению, вектор Бюргерса: то вектор Бюргерса находится графически как вектор, соединяющий конец контура Бюргерса с его началом.
 Правила построения вектора Бюргерса • Контур Бюргерса должен проходить только в «хорошем» материале, хотя может охватывать область «плохого» материала. • Во взаимно противоположных направлениях откладывается одинаковое число межатомных расстояний. • Обход по контуру Бюргерса осуществляется по часовой стрелке, если смотреть на контур из начала линии дислокации.
Правила построения вектора Бюргерса • Контур Бюргерса должен проходить только в «хорошем» материале, хотя может охватывать область «плохого» материала. • Во взаимно противоположных направлениях откладывается одинаковое число межатомных расстояний. • Обход по контуру Бюргерса осуществляется по часовой стрелке, если смотреть на контур из начала линии дислокации.
 Контур Бюргерса для краевой дислокации Ох1 и Ох2 направлены по соответствующим кристаллографическим осям недеформированной решетки. Контур abcda’: в направлении ab – 15 межатомных расстояний, bc – 13, cd – 15, da’ – 13. Контур незамкнут, а замыкающий его вектор аа’ – вектор Бюргерса. b ~ e 1 a. efghe’ – второй контур для той же дислокации, где b=e 1 a. Краевая дислокация – линейный дефект кристаллического строения с вектором, перпендикулярным оси дефекта.
Контур Бюргерса для краевой дислокации Ох1 и Ох2 направлены по соответствующим кристаллографическим осям недеформированной решетки. Контур abcda’: в направлении ab – 15 межатомных расстояний, bc – 13, cd – 15, da’ – 13. Контур незамкнут, а замыкающий его вектор аа’ – вектор Бюргерса. b ~ e 1 a. efghe’ – второй контур для той же дислокации, где b=e 1 a. Краевая дислокация – линейный дефект кристаллического строения с вектором, перпендикулярным оси дефекта.
 Контур Бюргерса для краевой дислокации При введении единичного вектора ξ, направленного по линии дислокации определение принимает вид: (b, ξ) = 0.
Контур Бюргерса для краевой дислокации При введении единичного вектора ξ, направленного по линии дислокации определение принимает вид: (b, ξ) = 0.
 Контур Бюргерса для краевой дислокации Для краевой дислокации в кристалле с частичным сдвигом, который осуществился в результате движения краевой дислокации по некоторой плоскости скольжения. Вектор Бюргерса является вектором смещения материала над той частью плоскости скольжения, по которой прошла дислокация, по отношению к материалу под плоскостью скольжения.
Контур Бюргерса для краевой дислокации Для краевой дислокации в кристалле с частичным сдвигом, который осуществился в результате движения краевой дислокации по некоторой плоскости скольжения. Вектор Бюргерса является вектором смещения материала над той частью плоскости скольжения, по которой прошла дислокация, по отношению к материалу под плоскостью скольжения.
 Контур Бюргерса для винтовой дислокации Начало контура – f, в направлении оси Ох2 – 4 межатомных расстояния, в направлении полуоси Ох3 – 13, Ох2 - 3. В обратных направлениях – то же. Т. о. получаем контур: f -> 18’’’ -> a -> b -> 2’’’ -> c -> d - > e. Винтовая дислокация – линейный дефект кристаллического строения с вектором Бюргерса, который параллелен оси дефекта.
Контур Бюргерса для винтовой дислокации Начало контура – f, в направлении оси Ох2 – 4 межатомных расстояния, в направлении полуоси Ох3 – 13, Ох2 - 3. В обратных направлениях – то же. Т. о. получаем контур: f -> 18’’’ -> a -> b -> 2’’’ -> c -> d - > e. Винтовая дислокация – линейный дефект кристаллического строения с вектором Бюргерса, который параллелен оси дефекта.
 Контур Бюргерса для винтовой дислокации При введении единичного вектора ξ, направленного по линии дислокации определение принимает вид: (b, ξ) = /b/. От вектора Бюргерса зависят другие характеристики дислокации. Для конкретной дислокации он постоянен вдоль всей линии дислокации. Смешанную дислокацию всегда можно представить как состоящую из отрезков чисто краевых и чисто винтовых дислокаций.
Контур Бюргерса для винтовой дислокации При введении единичного вектора ξ, направленного по линии дислокации определение принимает вид: (b, ξ) = /b/. От вектора Бюргерса зависят другие характеристики дислокации. Для конкретной дислокации он постоянен вдоль всей линии дислокации. Смешанную дислокацию всегда можно представить как состоящую из отрезков чисто краевых и чисто винтовых дислокаций.
 Плоскость скольжения дислокации – плоскость, в которой лежит линия дислокации (вектор ξ) и вектор Бюргерса дислокации. Орт n нормали к этой плоскости определяется соотношением: Краевая дислокация перемещается скольжением лишь в плоскости, в которой лежат ее линии и ее вектор Бюргерса. Для винтовой: любая плоскость, в которой лежит ее линия.
Плоскость скольжения дислокации – плоскость, в которой лежит линия дислокации (вектор ξ) и вектор Бюргерса дислокации. Орт n нормали к этой плоскости определяется соотношением: Краевая дислокация перемещается скольжением лишь в плоскости, в которой лежат ее линии и ее вектор Бюргерса. Для винтовой: любая плоскость, в которой лежит ее линия.
 Запись вектора Бюргерса Если в кубической решетке вектор Бюргерса дислокации это вектор решетки: d 101=ae 1+ae 2, т. е. b = ae 1+ae 2, то это записывают в виде: b = [a a 0] или b = a[110] – направление сдвига, величина сдвига: Дислокации, вектор Бюргерса которых равен по модулю а в любом направлении в пределах ячейки называют единичными дислокациями или дислокициями единичной мощности. В общем случае мощность дислокации с вектором Бюргерса а/n [uvw]:
Запись вектора Бюргерса Если в кубической решетке вектор Бюргерса дислокации это вектор решетки: d 101=ae 1+ae 2, т. е. b = ae 1+ae 2, то это записывают в виде: b = [a a 0] или b = a[110] – направление сдвига, величина сдвига: Дислокации, вектор Бюргерса которых равен по модулю а в любом направлении в пределах ячейки называют единичными дислокациями или дислокициями единичной мощности. В общем случае мощность дислокации с вектором Бюргерса а/n [uvw]:
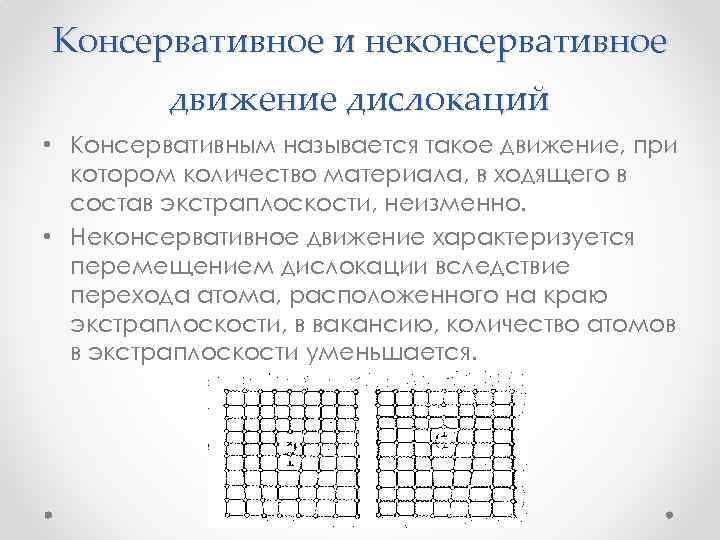 Консервативное и неконсервативное движение дислокаций • Консервативным называется такое движение, при котором количество материала, в ходящего в состав экстраплоскости, неизменно. • Неконсервативное движение характеризуется перемещением дислокации вследствие перехода атома, расположенного на краю экстраплоскости, в вакансию, количество атомов в экстраплоскости уменьшается.
Консервативное и неконсервативное движение дислокаций • Консервативным называется такое движение, при котором количество материала, в ходящего в состав экстраплоскости, неизменно. • Неконсервативное движение характеризуется перемещением дислокации вследствие перехода атома, расположенного на краю экстраплоскости, в вакансию, количество атомов в экстраплоскости уменьшается.
 Количество скольжения •
Количество скольжения •
 Количество скольжения •
Количество скольжения •
 Количество скольжения •
Количество скольжения •
 Количество скольжения •
Количество скольжения •
 Количество скольжения •
Количество скольжения •
 Плотность дислокаций •
Плотность дислокаций •
 Плотность дислокаций •
Плотность дислокаций •
 Сила, действующая на дислокацию – это сила, которая будучи приложена к линии дислокации, как к самостоятельному физическому объекту, вызовет перемещения материала, производимые реальными силами, приложенными к атомам кристалла. σ-все силы, Fds – сила, приложенная к элементу d. S дислокации. Под действием σ отрезок дислокации d. S перемещается на dl. В пределах площади d. Sdl каждый атом в верхней части кристалла сместился по отношению к нижней на расстояние /b/. К перемещенной на /b/ площадке приложена сила σd. Sdl.
Сила, действующая на дислокацию – это сила, которая будучи приложена к линии дислокации, как к самостоятельному физическому объекту, вызовет перемещения материала, производимые реальными силами, приложенными к атомам кристалла. σ-все силы, Fds – сила, приложенная к элементу d. S дислокации. Под действием σ отрезок дислокации d. S перемещается на dl. В пределах площади d. Sdl каждый атом в верхней части кристалла сместился по отношению к нижней на расстояние /b/. К перемещенной на /b/ площадке приложена сила σd. Sdl.
 Сила, действующая на дислокацию Первый способ вычисления силы: Отрезок d. S под действием силы Fds переместился на расстояние dl, при этом произведена работа d. A=(Fds)dl. Площадка d. Sdl под действием силы σd. Sdl переместилась на расстояние /b/, при этом произведена работа d. A=(σd. Sdl)/b/. Приравняем: Fds=/b/σd. S. Сила, действующая на единицу длины линии дислокации: F=σ/b/.
Сила, действующая на дислокацию Первый способ вычисления силы: Отрезок d. S под действием силы Fds переместился на расстояние dl, при этом произведена работа d. A=(Fds)dl. Площадка d. Sdl под действием силы σd. Sdl переместилась на расстояние /b/, при этом произведена работа d. A=(σd. Sdl)/b/. Приравняем: Fds=/b/σd. S. Сила, действующая на единицу длины линии дислокации: F=σ/b/.
 Сила, действующая на дислокацию •
Сила, действующая на дислокацию •
 Движение дислокаций в произвольном поле напряжений •
Движение дислокаций в произвольном поле напряжений •
 Движение дислокаций в произвольном поле напряжений В то же время сила F входит в выражение для работы, производимой силами поля упругих напряжений над дислокацией при ее перемещении на dl: d. A=(F, dl). Воспользуемся выражением для F, что определить силу, действующую на дислокацию в произвольном поле напряжений, которое задается тензором σlk (x, y, z). При этом следует отметить: перемещение вектора ξ линии дислокации параллельно самому себе на вектор dl приводит к смещению площадки /ξ х dl/ на вектор b.
Движение дислокаций в произвольном поле напряжений В то же время сила F входит в выражение для работы, производимой силами поля упругих напряжений над дислокацией при ее перемещении на dl: d. A=(F, dl). Воспользуемся выражением для F, что определить силу, действующую на дислокацию в произвольном поле напряжений, которое задается тензором σlk (x, y, z). При этом следует отметить: перемещение вектора ξ линии дислокации параллельно самому себе на вектор dl приводит к смещению площадки /ξ х dl/ на вектор b.
 Движение дислокаций в произвольном поле напряжений Движение дислокации состоит из чередующихся коротких скольжений и консервативных переходов. Необходимой комбинацией таких элементов движения можно обеспечить перемещение отрезка дислокации параллельно самому себе в любом направлении.
Движение дислокаций в произвольном поле напряжений Движение дислокации состоит из чередующихся коротких скольжений и консервативных переходов. Необходимой комбинацией таких элементов движения можно обеспечить перемещение отрезка дислокации параллельно самому себе в любом направлении.
 Движение дислокаций в произвольном поле напряжений σn – напряжение, действующее на площадке d. S=/ξ x dl/. Сила, приложенная к площадке: σn /d. S/ = σn =/ξ x dl/. Следовательно, работа, произведенная силами поля напряжений σlk при перемещении площадки d. S на b: d. A=((σnd. S), b). Произведение σn /d. S/ можно выразить через компоненты тензора напряжений и проекции d. S 1, d. S 2, d. S 3 площадки на координатные оси d. S 1 = SOBC, d. S 2 =SAOC, d. S 1=SAOB, /d. S 1/=SABC. σn /d. S/= σ1 d. S 1 + σ2 d. S 2 + σ3 d. S 3.
Движение дислокаций в произвольном поле напряжений σn – напряжение, действующее на площадке d. S=/ξ x dl/. Сила, приложенная к площадке: σn /d. S/ = σn =/ξ x dl/. Следовательно, работа, произведенная силами поля напряжений σlk при перемещении площадки d. S на b: d. A=((σnd. S), b). Произведение σn /d. S/ можно выразить через компоненты тензора напряжений и проекции d. S 1, d. S 2, d. S 3 площадки на координатные оси d. S 1 = SOBC, d. S 2 =SAOC, d. S 1=SAOB, /d. S 1/=SABC. σn /d. S/= σ1 d. S 1 + σ2 d. S 2 + σ3 d. S 3.
 Движение дислокаций в произвольном поле напряжений Далее σ1 = е 1 σ11+ е 2 σ21 + е 3σ31; σ2 = е 1 σ12+ е 2 σ22 + е 3σ32; σ3 = е 1 σ13+ е 2 σ23 + е 3σ33; И σn/d. S/= е 1 (σ11 d. S 1 + σ12 d. S 2 + σ13 d. S 3)+ е 2 (σ21 d. S 1 + σ22 d. S 2 + σ23 d. S 3)+ е 3 (σ31 d. S 1 + σ32 d. S 2 + σ33 d. S 3). В правой части стоит вектор, проекции которого на координатные оси представляют собой комбинации из компонентов тензора σlk и проекций вектора d. S на координатные оси.
Движение дислокаций в произвольном поле напряжений Далее σ1 = е 1 σ11+ е 2 σ21 + е 3σ31; σ2 = е 1 σ12+ е 2 σ22 + е 3σ32; σ3 = е 1 σ13+ е 2 σ23 + е 3σ33; И σn/d. S/= е 1 (σ11 d. S 1 + σ12 d. S 2 + σ13 d. S 3)+ е 2 (σ21 d. S 1 + σ22 d. S 2 + σ23 d. S 3)+ е 3 (σ31 d. S 1 + σ32 d. S 2 + σ33 d. S 3). В правой части стоит вектор, проекции которого на координатные оси представляют собой комбинации из компонентов тензора σlk и проекций вектора d. S на координатные оси.
 Движение дислокаций в произвольном поле напряжений Логично назвать этот вектор скалярным произведением тензора σlk на вектор d. S. В тензорном исчислении таким образом вводится понятие скалярного произведения тензора 2 ранга на вектор в правой части уравнения: Под скалярным произведением тензора plk 2 ранга на вектор а справа понимается вектор: a’=(plk, a), равный: a’=e 1(p 1, a) + e 2(p 2, a) + e 3(p 3, a) или a’=e 1(p 11 a 1 +p 12 a 2 + p 13 a 3) + e 2(p 21 a 1 +p 22 a 2 + p 23 a 3) + e 3 (p 31 a 1 +p 32 a 2 + p 33 a 3).
Движение дислокаций в произвольном поле напряжений Логично назвать этот вектор скалярным произведением тензора σlk на вектор d. S. В тензорном исчислении таким образом вводится понятие скалярного произведения тензора 2 ранга на вектор в правой части уравнения: Под скалярным произведением тензора plk 2 ранга на вектор а справа понимается вектор: a’=(plk, a), равный: a’=e 1(p 1, a) + e 2(p 2, a) + e 3(p 3, a) или a’=e 1(p 11 a 1 +p 12 a 2 + p 13 a 3) + e 2(p 21 a 1 +p 22 a 2 + p 23 a 3) + e 3 (p 31 a 1 +p 32 a 2 + p 33 a 3).
 Движение дислокаций в произвольном поле напряжений Под скалярным произведением plk на вектор а понимают новый вектор а’’, равный: a’’=(a, plk) = (a, e 1) p 1 + (a, e 2) p 2 + (a, e 3) p 3 или a’’=(a, plk) = e 1(p 11 a 1 +p 12 a 2 + p 13 a 3) + e 2(p 21 a 1 +p 22 a 2 + p 23 a 3) + e 3 (p 31 a 1 +p 32 a 2 + p 33 a 3). Таким образом: σn /d. S/ = (σlk d. S). Поскольку d. S =/ξ x dl/, то σn /d. S/ = (σlk, /ξ x dl/). В соответствии с выражением d. A=((σnd. S), b), d. A=((σlk, /ξ x dl/), b). В то же время d. A=(f, dl), где l – сила, действующая на единицу дислокации.
Движение дислокаций в произвольном поле напряжений Под скалярным произведением plk на вектор а понимают новый вектор а’’, равный: a’’=(a, plk) = (a, e 1) p 1 + (a, e 2) p 2 + (a, e 3) p 3 или a’’=(a, plk) = e 1(p 11 a 1 +p 12 a 2 + p 13 a 3) + e 2(p 21 a 1 +p 22 a 2 + p 23 a 3) + e 3 (p 31 a 1 +p 32 a 2 + p 33 a 3). Таким образом: σn /d. S/ = (σlk d. S). Поскольку d. S =/ξ x dl/, то σn /d. S/ = (σlk, /ξ x dl/). В соответствии с выражением d. A=((σnd. S), b), d. A=((σlk, /ξ x dl/), b). В то же время d. A=(f, dl), где l – сила, действующая на единицу дислокации.
 Движение дислокаций в произвольном поле напряжений Прямым вычислением можно убедиться, что: ((σlk [a x c]), b) = ([b, σlk ) x a], c). Вернемся к равенствам для d. A. C учетом записанного выше, d. A=((σlk, /ξ x dl/), b) можно записать в виде: d. A=([(b, σlk) x ξ] dl), сравнение которого с d. A=(f, dl) приводит к равенству: f = [(b, σlk) x ξ] – формула Пича-Келера. В проекциях на оси эта формула имеет вид: f 1 = (b, σlk)2 ξ 3 - (b, σlk)3 ξ 2 ; f 2 = (b, σlk)3 ξ 1 - (b, σlk)1 ξ 3 ; f 1 = (b, σlk)1 ξ 2 - (b, σlk)2 ξ 1.
Движение дислокаций в произвольном поле напряжений Прямым вычислением можно убедиться, что: ((σlk [a x c]), b) = ([b, σlk ) x a], c). Вернемся к равенствам для d. A. C учетом записанного выше, d. A=((σlk, /ξ x dl/), b) можно записать в виде: d. A=([(b, σlk) x ξ] dl), сравнение которого с d. A=(f, dl) приводит к равенству: f = [(b, σlk) x ξ] – формула Пича-Келера. В проекциях на оси эта формула имеет вид: f 1 = (b, σlk)2 ξ 3 - (b, σlk)3 ξ 2 ; f 2 = (b, σlk)3 ξ 1 - (b, σlk)1 ξ 3 ; f 1 = (b, σlk)1 ξ 2 - (b, σlk)2 ξ 1.
 Силы, действующие в поле напряжений на краевую дислокацию вдоль оси Ох3 b ┴ ξ, ξ 3 = 1, ξ 1 = ξ 2 = 0, /b 1/= /b/, b 2 = b 3 = 0 и f 1 = b σ12; f 2 = - b σ11; f 3 = 0.
Силы, действующие в поле напряжений на краевую дислокацию вдоль оси Ох3 b ┴ ξ, ξ 3 = 1, ξ 1 = ξ 2 = 0, /b 1/= /b/, b 2 = b 3 = 0 и f 1 = b σ12; f 2 = - b σ11; f 3 = 0.
 Силы, действующие в поле напряжений на винтовую дислокацию вдоль оси Ох3 b ║ ξ, b 1 = b 2 = 0, b 3 = /b/ = b, ξ 1 = ξ 2 = 0, ξ 3 = 1. Следовательно: f 1 = b σ32; f 2 = - b σ31; f 3 = 0. Т. о. сила, действующая на единицу как краевой, так и винтовой дислокации, направлена перпендикулярно линии дислокации, т. к. в обоих случаях f 3 = 0. Поскольку любую дислокацию можно представить в виде разложения на взаимно перпендикулярные краевые и винтовые компоненты, то это утверждение справедливо в общем случае.
Силы, действующие в поле напряжений на винтовую дислокацию вдоль оси Ох3 b ║ ξ, b 1 = b 2 = 0, b 3 = /b/ = b, ξ 1 = ξ 2 = 0, ξ 3 = 1. Следовательно: f 1 = b σ32; f 2 = - b σ31; f 3 = 0. Т. о. сила, действующая на единицу как краевой, так и винтовой дислокации, направлена перпендикулярно линии дислокации, т. к. в обоих случаях f 3 = 0. Поскольку любую дислокацию можно представить в виде разложения на взаимно перпендикулярные краевые и винтовые компоненты, то это утверждение справедливо в общем случае.
 Упругие свойства дислокаций Под упругими свойствами понимают упругие деформации и напряжения, которые создаются дислокациями в той среде, в которой они находятся. . Теория, в которой поля деформаций и напряжений вокруг дислокаций вычисляются методами теории упругости, называются континуальной теорией дислокаций. Дислокации в упругом континууме называются дислокациями Вольтерра.
Упругие свойства дислокаций Под упругими свойствами понимают упругие деформации и напряжения, которые создаются дислокациями в той среде, в которой они находятся. . Теория, в которой поля деформаций и напряжений вокруг дислокаций вычисляются методами теории упругости, называются континуальной теорией дислокаций. Дислокации в упругом континууме называются дислокациями Вольтерра.
 Упругие свойства дислокаций Для расчета используются уравнения теории упругости, компоненты тензора напряжений и тензора деформаций как функции координат точек среды. Восемнадцать функций ulk (x, y, z) и σlk (x, y, z) полностью описываю поля деформаций и напряжений вокруг дислокаций. Создание дислокаций Вольтерра в упругой среде позволяет экспериментально исследовать возникающие вокруг дислокации поля напряжений. Мысленное создание дислокаций Вольтерра дает возможность установить характер деформации среды и сформулировать условия задачи, решаемой далее методами теории упругости.
Упругие свойства дислокаций Для расчета используются уравнения теории упругости, компоненты тензора напряжений и тензора деформаций как функции координат точек среды. Восемнадцать функций ulk (x, y, z) и σlk (x, y, z) полностью описываю поля деформаций и напряжений вокруг дислокаций. Создание дислокаций Вольтерра в упругой среде позволяет экспериментально исследовать возникающие вокруг дислокации поля напряжений. Мысленное создание дислокаций Вольтерра дает возможность установить характер деформации среды и сформулировать условия задачи, решаемой далее методами теории упругости.
 Упругие свойства дислокаций Этапы образования дислокаций Вольтерра: 1. Выделим в упругой среде некоторый объем, в пределах которого будем образовывать дислокацию. Этот объем может иметь любую форму, но целесообразной является форма цилиндра, соответствующего форме дефекта. 2. Создадим модель плоскости скольжения: сделаем разрез по плоскости ABCD. 3. Удалим область «плохого» материала – высверлим материал вдоль оси Ox 3. 4. Сдвинем по плоскости разреза верхнюю часть цилиндра относительно нижней на расстояние b и склеим материал по плоскости разреза.
Упругие свойства дислокаций Этапы образования дислокаций Вольтерра: 1. Выделим в упругой среде некоторый объем, в пределах которого будем образовывать дислокацию. Этот объем может иметь любую форму, но целесообразной является форма цилиндра, соответствующего форме дефекта. 2. Создадим модель плоскости скольжения: сделаем разрез по плоскости ABCD. 3. Удалим область «плохого» материала – высверлим материал вдоль оси Ox 3. 4. Сдвинем по плоскости разреза верхнюю часть цилиндра относительно нижней на расстояние b и склеим материал по плоскости разреза.
 Поля напряжений и деформаций винтовой дислокации Материал смещается только вдоль оси Ох3, в перпендикулярных направлениях смещения отсутствуют. Т. о. составляющие вектора деформации u u 1 и u 2 равны 0. u 3 не зависит от координаты х3 – смещения материала вдоль оси х3 одинаковы для всех точек, имеющих фиксированные значения координат х1 и х2.
Поля напряжений и деформаций винтовой дислокации Материал смещается только вдоль оси Ох3, в перпендикулярных направлениях смещения отсутствуют. Т. о. составляющие вектора деформации u u 1 и u 2 равны 0. u 3 не зависит от координаты х3 – смещения материала вдоль оси х3 одинаковы для всех точек, имеющих фиксированные значения координат х1 и х2.
 Поля напряжений и деформаций винтовой дислокации Поскольку u 1 = u 2 и u 3 ≠ u 3 (x 3), то Уравнение (1 - 2μ) ∆μ + grad div u = 0 в данном случае принимает вид: ∆u = 0 или
Поля напряжений и деформаций винтовой дислокации Поскольку u 1 = u 2 и u 3 ≠ u 3 (x 3), то Уравнение (1 - 2μ) ∆μ + grad div u = 0 в данном случае принимает вид: ∆u = 0 или
 Поля напряжений и деформаций винтовой дислокации Вид функции u 3 (x 1, х2) можно найти, используя соображения о характере сдвиговой деформации, обусловленно наличием винтовой дислокации. θ – угловая координата. При ее возрастании сдвиг материала вдоль Ох3 непрерывно увеличивается и при θ = 2 линейное смещение любой точки в плоскости х1 Ох2 равно b, и функция обладает свойствами: u 3(r, θ, x 3) = 0, U 3(r, 2 , x 3) = b.
Поля напряжений и деформаций винтовой дислокации Вид функции u 3 (x 1, х2) можно найти, используя соображения о характере сдвиговой деформации, обусловленно наличием винтовой дислокации. θ – угловая координата. При ее возрастании сдвиг материала вдоль Ох3 непрерывно увеличивается и при θ = 2 линейное смещение любой точки в плоскости х1 Ох2 равно b, и функция обладает свойствами: u 3(r, θ, x 3) = 0, U 3(r, 2 , x 3) = b.
 Поля напряжений и деформаций винтовой дислокации u 3(r, θ, x 3) должна удовлетворять Простейшим видом функции, которая удовлетворяет условиям u 3(r, θ, x 3) = 0 U 3(r, 2 , x 3) = b является функция: В декартовых координатах эта функция приобретает вид:
Поля напряжений и деформаций винтовой дислокации u 3(r, θ, x 3) должна удовлетворять Простейшим видом функции, которая удовлетворяет условиям u 3(r, θ, x 3) = 0 U 3(r, 2 , x 3) = b является функция: В декартовых координатах эта функция приобретает вид:
 Поля напряжений и деформаций винтовой дислокации Проверим, удовлетворяет ли эта функция уравнению : Таким образом, равенство выполняется.
Поля напряжений и деформаций винтовой дислокации Проверим, удовлетворяет ли эта функция уравнению : Таким образом, равенство выполняется.
 Поля напряжений и деформаций винтовой дислокации Матрица тензора деформации винтовой дислокации имеет вид:
Поля напряжений и деформаций винтовой дислокации Матрица тензора деформации винтовой дислокации имеет вид:
 Поля напряжений и деформаций винтовой дислокации Компоненты тензора напряжений: Таким образом, поле деформации винтовой дислокации содержит только сдвиговые деформации. В поле напряжений винтовой дислокации нет нормальных напряжений, а есть касательные.
Поля напряжений и деформаций винтовой дислокации Компоненты тензора напряжений: Таким образом, поле деформации винтовой дислокации содержит только сдвиговые деформации. В поле напряжений винтовой дислокации нет нормальных напряжений, а есть касательные.
 Поля напряжений и деформаций краевой дислокации При краевой дислокации, расположенной вдоль оси Ох3, b 1=b, b 2=b 3=0, вектор деформации u лежит в плоскости х1 Ох2 и не зависит от х3. U 1 = u 1 (x 1, x 2); U 2 = u 2 (x 1, x 2); U 1 = 0.
Поля напряжений и деформаций краевой дислокации При краевой дислокации, расположенной вдоль оси Ох3, b 1=b, b 2=b 3=0, вектор деформации u лежит в плоскости х1 Ох2 и не зависит от х3. U 1 = u 1 (x 1, x 2); U 2 = u 2 (x 1, x 2); U 1 = 0.
 Поля напряжений и деформаций краевой дислокации Решение уравнений теории упругости дает, в этом случае, следующие выражения для многокомпонентных тензоров напряжений: Постоянную D находят:
Поля напряжений и деформаций краевой дислокации Решение уравнений теории упругости дает, в этом случае, следующие выражения для многокомпонентных тензоров напряжений: Постоянную D находят:
 Поля напряжений и деформаций краевой дислокации В цилиндрических координатах:
Поля напряжений и деформаций краевой дислокации В цилиндрических координатах:
 Поля напряжений и деформаций краевой дислокации Поскольку D>0, знак напряжений σхх и σху определяется знаком переменой у. Если у>0, то σхх<0 и наоборот. Знак σуу определяется как знаком у, так и знаком х2 - у2. Т. е. для положительной краевой дислокации материал вдоль оси Ох1 выше плоскости скольжения сжат, ниже – растянут. При /х/>/y/ и у >0 σуу >0 – материал вдоль оси Ох2 растянут и при /х/0 – сжат. Если у<0 и /х/>/y/, то σуу >0.
Поля напряжений и деформаций краевой дислокации Поскольку D>0, знак напряжений σхх и σху определяется знаком переменой у. Если у>0, то σхх<0 и наоборот. Знак σуу определяется как знаком у, так и знаком х2 - у2. Т. е. для положительной краевой дислокации материал вдоль оси Ох1 выше плоскости скольжения сжат, ниже – растянут. При /х/>/y/ и у >0 σуу >0 – материал вдоль оси Ох2 растянут и при /х/0 – сжат. Если у<0 и /х/>/y/, то σуу >0.


