ФИЗИКА Лектор Эйсмонт Наталья Геннадьевна доцент кафедры

ФИЗИКА

Лектор: Эйсмонт Наталья Геннадьевна, доцент кафедры физики Ом. ГТУ Меня можно найти: ь по расписанию на кафедре физики (главный корпус, 3 этаж) ь в ауд. Г-209 (преподавательская) или в ауд. Г-311

ЧТО ИЗУЧАЕТ ФИЗИКА? Физика (от греческого physis - природа) – наука о природе, изучающая простейшие и вместе с тем наиболее общие закономерности природы, cтроение и законы движения материи.

ь Механика. ь Молекулярная физика. Термодинамика. 2 семестр: ь Электричество. ь Магнетизм. 3 семестр: ь Колебания и волны. Волновая оптика. ь Атомная и ядерная физика. 1 семестр: Форма отчетности: экзамен. Допуск к экзамену: выполнены ВСЕ лабораторные работы - 40 баллов. Дополн. баллы: 2 провер. работы (max 10 балов); работа на практ. занятиях (max 9 баллов) коллоквиум (max 10 баллов). ИТОГО: max 69 баллов, min 40 баллов.

МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕРМОДИНАМИКА. Список учебной литературы для I семестра: Учебники и конспекты лекций 1. Трофимова Т. И. Курс физики: учебное пособие для вузов. – М. : Издательский центр «Академия» , 2010. – 560 с. 2. Данилов С. В. Классическая и релятивистская механика: конспект лекций / С. В. Данилов. // – Омск : Изд–во Ом. ГТУ, 2008. – 60 с. 3. Суриков В. И. Молекулярная физика и термодинамика: конспект лекций. / Вал. И. Суриков. // – Омск : Изд–во Ом. ГТУ, 2008. – 64 с. Методические указания по лабораторному практикуму 1. Иванов В. Н. Введение в лабораторный практикум по физике: учеб. пособие / В. Н. Иванов и др. // – Омск : Изд–во Ом. ГТУ, 2009. – 38 с. 2. Механика. Лабораторный практикум по физике. Иванов В. Н. , Иванова Г. П. , Кондратьева Т. Н. и др. // Издательство Ом. ГТУ. – 2008 г. – 48 с. (Г-306) 3. Механика. Методические указания к лабораторным работам. Иванов В. Н. , Бердинская Н. В. , Егорова В. А. и др. // Издательство Ом. ГТУ. – 2006 г. – 44 с. (Г 308)

Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.

В зависимости от скорости движения изучаемых тел МЕХАНИКА Нерелятивистская Релятивистская рассматривает движение тел со скоростями, значительно меньшими скорости света в вакууме V << c рассматривает движение тел со скоростями порядка скорости света в вакууме V~ c Скорость света в вакууме c=3· 108 м/с Рекорд скорости передвижения человека: основной модуль «Аполлона 10» (26 мая 1969 г. ) V = 39. 9 тыс. км/ч V ~ 0. 000037 c Большой Адронный Коллайдер Энергия протонов: Е=2. 36 Тэ. В Скорость протонов: V=0. 9999 c Рекорд скорости космического аппарата: солнечный зонд «Гелиос-Б» (15 января 1976 г. ) V=240 тыс. км/ч V~ 0. 00022 c Скорость космических лучей: V ~ c

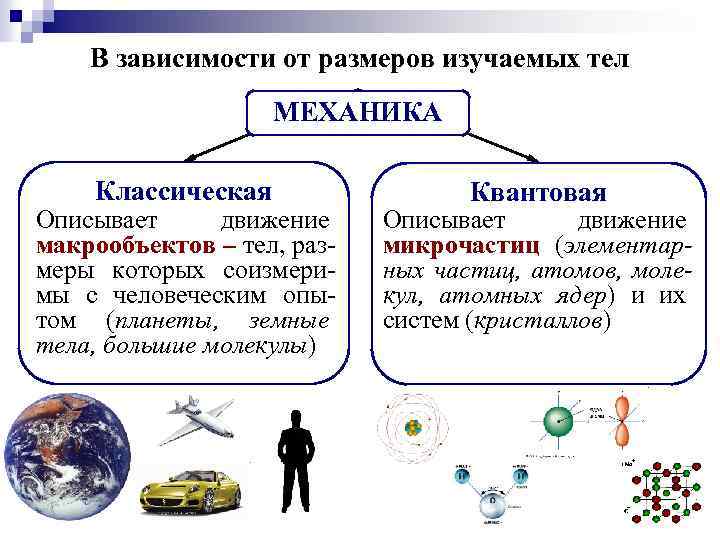В зависимости от размеров изучаемых тел МЕХАНИКА Классическая Описывает движение макрообъектов – тел, размеры которых соизмеримы с человеческим опытом (планеты, земные тела, большие молекулы) Квантовая Описывает движение микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (кристаллов)

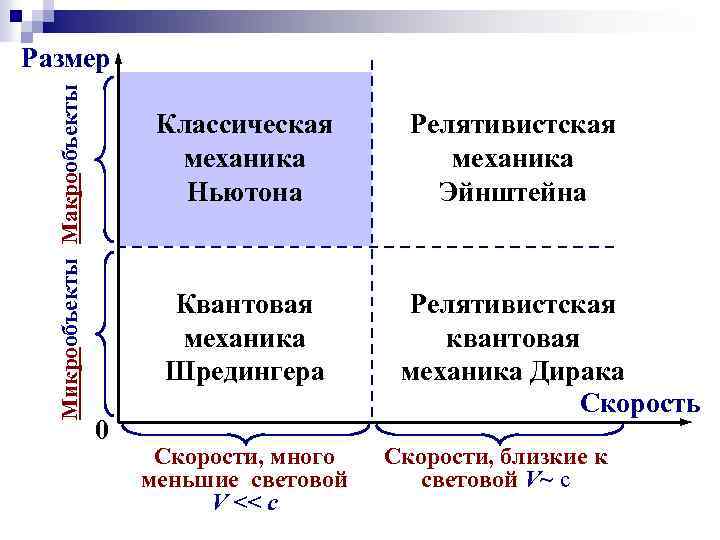Микрообъекты Макрообъекты Размер Классическая механика Ньютона Квантовая механика Шредингера 0 Скорости, много меньшие световой V << c Релятивистская механика Эйнштейна Релятивистская квантовая механика Дирака Скорость Скорости, близкие к световой V~ c

Всякое движение твердого тела можно разложить на два основных вида движения: поступательное и вращательное. Поступательное движение – это движение, при котором все точки тела движутся по одинаковым траекториям.

Вращательное движение – это движение, при котором траектории всех точек тела являются окружностями с центрами лежащими на общей оси (оси вращения).

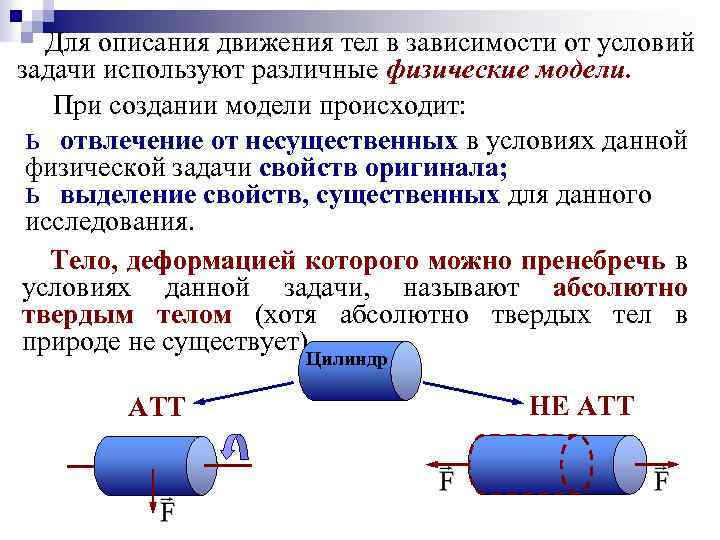Для описания движения тел в зависимости от условий задачи используют различные физические модели. При создании модели происходит: ь отвлечение от несущественных в условиях данной физической задачи свойств оригинала; ь выделение свойств, существенных для данного исследования. Тело, деформацией которого можно пренебречь в условиях данной задачи, называют абсолютно твердым телом (хотя абсолютно твердых тел в природе не существует). Цилиндр АТТ НЕ АТТ

Абсолютно твердое тело? ДА НЕТ

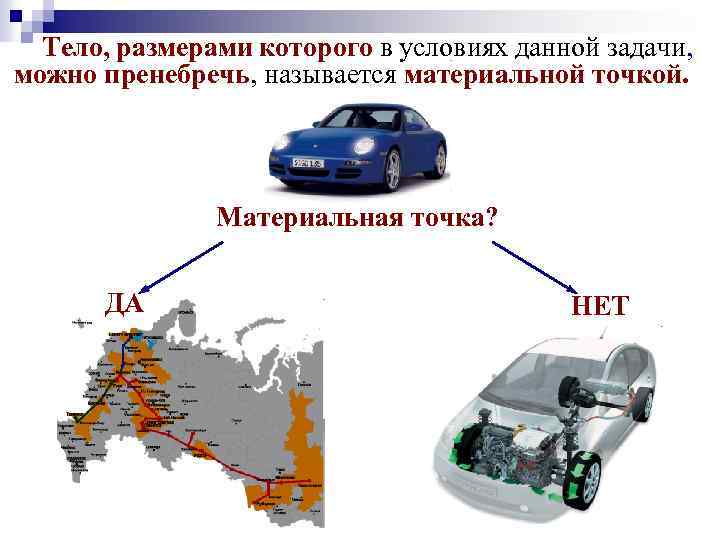Тело, размерами которого в условиях данной задачи, можно пренебречь, называется материальной точкой. Материальная точка? ДА НЕТ

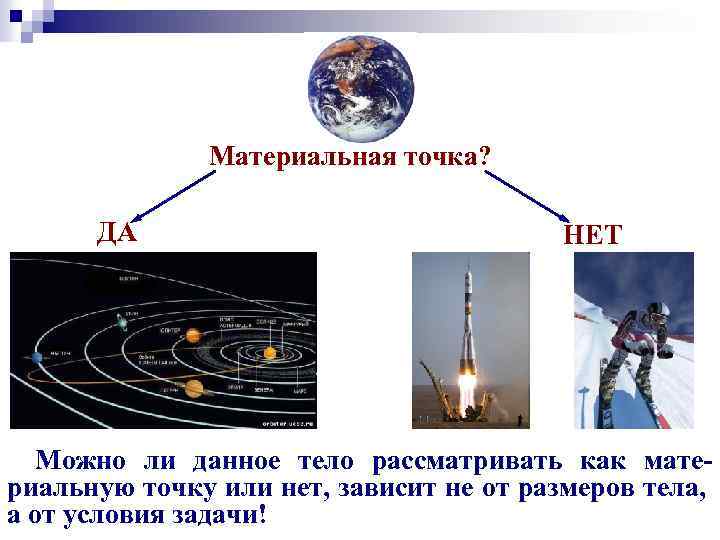Материальная точка? ДА НЕТ Можно ли данное тело рассматривать как материальную точку или нет, зависит не от размеров тела, а от условия задачи!

ОСНОВНЫЕ РАЗДЕЛЫ МЕХАНИКИ (в зависимости от решаемых задач): Кинематика – изучает основные характеристики движения (координаты, скорость, ускорение, …). Динамика –изучает причины движения и его изменения (силы). Статика –изучает условия равновесия тел (силы и моменты сил).

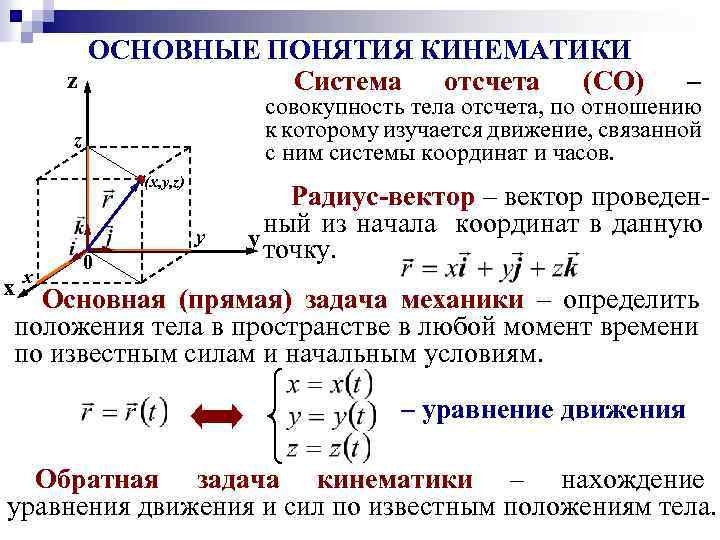ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ z Система отсчета (СО) совокупность тела отсчета, по отношению к которому изучается движение, связанной с ним системы координат и часов. z (x, y, z) y x x – 0 Радиус-вектор – вектор проведенный из начала координат в данную y точку. Основная (прямая) задача механики – определить положения тела в пространстве в любой момент времени по известным силам и начальным условиям. – уравнение движения Обратная задача кинематики – нахождение уравнения движения и сил по известным положениям тела.

y r Геометрическое место точек концов радиус r 4 векторов называется r 3 траекторией точки. Длина траектории называется путь ΔS. r 2 r 1 O x Вектор, соединяющий начальное и конечное положение тела называется перемещением r. r – это приращение радиус-вектора за время t

КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

Кинематические характеристики движения 1. Скорость материальной точки Скорость характеризует быстроту движения Средняя скорость – это есть отношение вектора перемещения ко времени, за которое это перемещение произошло y Vcp ↑↑ r Модуль средней скорости: Средняя путевая скорость – это отношение пути ко времени, за которое этот путь пройден r 1 O 1 r 2 Vcp r 2 x

Мгновенная скорость – это скорость в данный момент времени, в данной точке траектории. Мгновенная скорость – это предел, к которому стремится средняя скорость при Δt → 0 Мгновенная скорость – это первая производная радиус вектора по времени Проекции вектора скорости на оси координат: Модуль вектора мгновенной скорости: Если задан путь S(t), то V 1 2 1 Vcp V 2

Вектор мгновенной скорости направлен по касательной к траектории V V V V

2. Ускорение материальной точки Ускорение характеризует быстроту изменения скорости Мгновенное ускорение – это первая производная мгновенной скорости по времени Проекции вектора ускорения на оси координат:

Нормальное ускорение характеризует изменение скорости по направлению и направлено по нормали к траектории. Если прямолинейное движение: Тангенциальное ускорение характеризует изменение величины (модуля) скорости и направлено по касательной к траектории. Если равномерное движение: замедл. движ. ускоренное движение: 2 1 ускорен. движ. замедленное движение:

Нельзя не знать! – тангенциальное – нормальное ускорение – направлен в центр кривизны траектории прямолинейное движение: – направлен вдоль касательной к траектории равномерное движение: замедл. движ. ускоренное движение: 2 1 ускорен. движ. замедленное движение:

Нельзя не знать! – мгновенное ускорение (характеризует быстроту изменения скорость в данный момент времени, в данной точке траектории) или – полное ускорение – тангенциальное ускорение (характеризует быстроту изменения модуля скорости) – нормальное ускорение (характеризует быстроту изменения направления скорости)

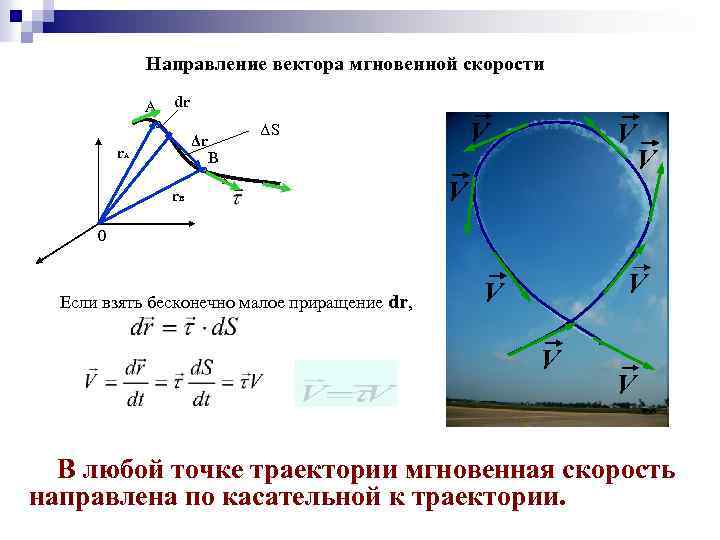Направление вектора мгновенной скорости А dr Δr В r. A V ΔS r. B V V V 0 Если взять бесконечно малое приращение dr, V V В любой точке траектории мгновенная скорость направлена по касательной к траектории.

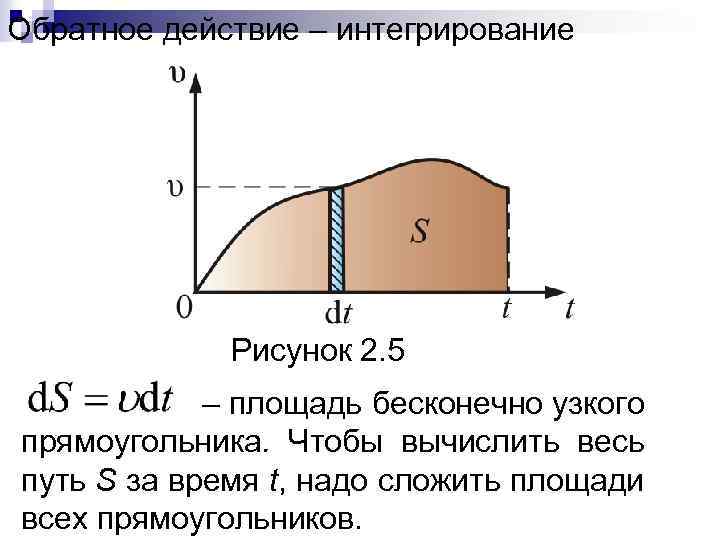Обратное действие – интегрирование Рисунок 2. 5 – площадь бесконечно узкого прямоугольника. Чтобы вычислить весь путь S за время t, надо сложить площади всех прямоугольников.

Ускорение – это мера изменения скорости со временем • Среднее ускорение – это отношение вектора изменения скорости ко времени, за которое это изменение произошло (2. 10) (2. 9) • Мгновенное ускорение – это предел, к которому стремится среднее ускорение при Δt→ 0 Ускорение - это (2. 11) Учитывая, что первая производная скорости по времени , получим (2. 12) Ускорение – это вторая производная радиус-вектора по времени

проекции вектора ускорения на оси координат где Вектор ускорения в этом случае будет иметь вид Модуль вектора ускорения (2. 12) (2. 13) В общем случае, при криволинейном движении, мгновенная скорость может изменяться как по величине, так и по направлению. Найдем ускорение в этом случае.

Мы знаем, что вектор мгновенной скорости направлен всегда по касательной к траектории, то есть Это сложная функция, так как τ и V (2. 14) зависят от времени, причем τ зависит от времени через S Найдем первую производную скорости (2. 14) по времени (2. 15) , где или (2. 17) С учетом (2. 15), получим R – радиус кривизны, - нормаль, вектор ┴ к τ и направленный к центру кривизны Первое слагаемое в формуле (2. 17) характеризует изменение величины (модуля) скорости и имеет направление, совпадающее с , то есть с касательной к траектории. Это ускорение называют тангенциальным линейным ускорением (2. 18) - вектор тангенциального ускорения (2. 19) - величина (модуль) тангенциального ускорения

Второе слагаемое в формуле (2. 17) характеризует изменение скорости по направлению и направлено по нормали Его называют нормальным или центростремительным ускорением (2. 21) - модуль нормального ускорения (2. 20) - вектор нормального ускорения Таким образом, вектор полного ускорения при любом криволинейном и движении может быть представлен в виде суммы двух векторов (2. 22) Так как (всегда ), то модуль полного ускорения равен (2. 23)