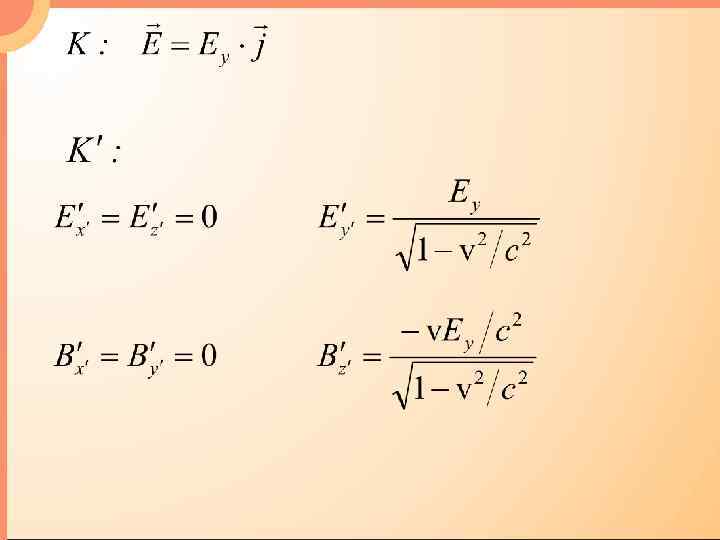Физика ч II Электричество и магнетизм Лекция

Физика ч. II «Электричество и магнетизм»

Лекция № 10 «Уравнения Максвелла»

Лекцию читает Чуркин Юрий Валентинович доцент каф. физики, кандидат физико-математических наук FТелефон кафедры: 8 -812 -314 -26 -40 Fe-mail: yuch 58@yandex. ru physics@nwpi. ru

Тема 10. Уравнения Максвелла. 10. 1. Общая характеристика теории Максвелла. Основная задача электродинамики – найти характеристики электромагнитного поля для заданной системы электрических зарядов и токов. • Теория Максвелла – феноменологическая теория – свойства среды характеризуют ε, μ и σ. • Теория Максвелла – макроскопическая теория.

Теорема Гаусса утверждает: поток вектора а, характеризующего какое-либо поле, через произвольную замкнутую поверхность S, мысленно проведенную в это поле, равен интегралу от дивергенции вектора а, взятому по объему V, ограниченному замкнутой поверхностью S: где ах, ay, az – проекции вектора а на оси прямоугольной декартовой системы координат.

Теорема Стокса утверждает: циркуляция вектора а, характеризующего какое-либо поле, вдоль произвольного замкнутого контура L, мысленно проведенного в этом поле, равна потоку вектора rot а через поверхность S, опирающуюся на контур L: Здесь rot a – ротор вектора а, который выражается в декартовых координатах следующим образом:

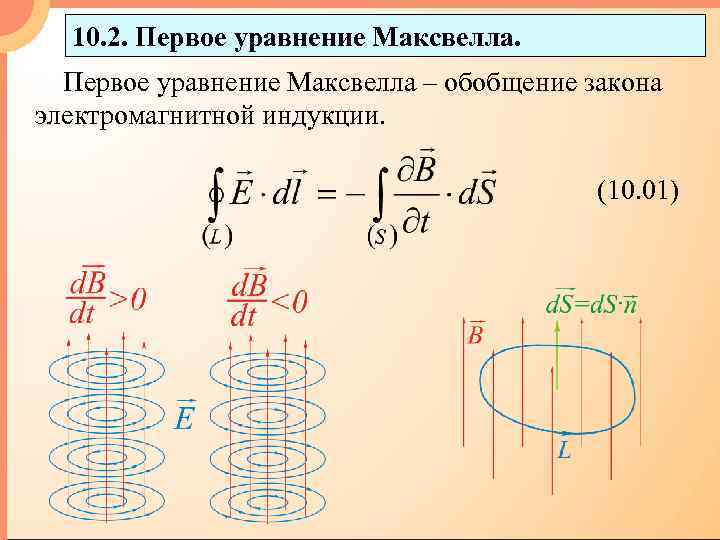10. 2. Первое уравнение Максвелла – обобщение закона электромагнитной индукции. (10. 01)

Циркуляция вектора Е напряженности электрического поля по произвольному неподвижному замкнутому контуру, мысленно проведенному в электромагнитном поле, равна взятому с обратным знаком потоку вектора через поверхность S, ограниченную этим контуром. (10. 02)

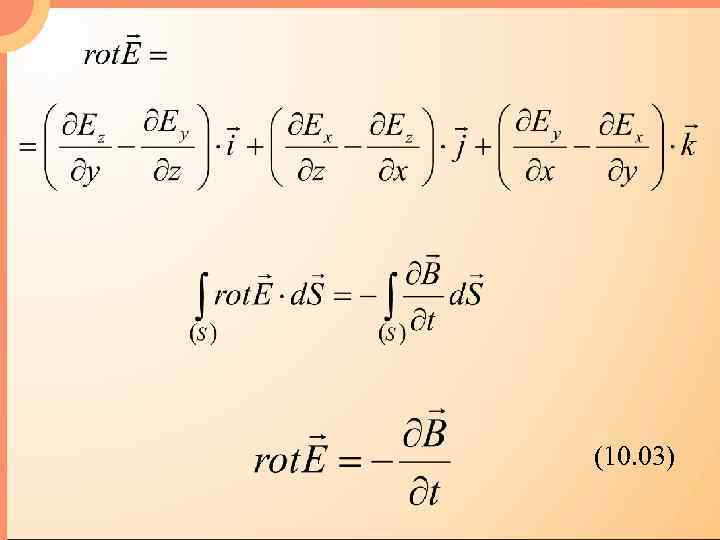(10. 03)

10. 3. Ток смещения. Второе уравнение Максвелла – обобщение закона полного тока.

(10. 04) Плотность тока смещения в данной точке пространства равна скорости изменения вектора электрического смещения в этой точке. Током смещения сквозь произвольную поверхность S называется физическая величина, численно равная потоку вектора плотности тока смещения сквозь эту поверхность. (10. 05)

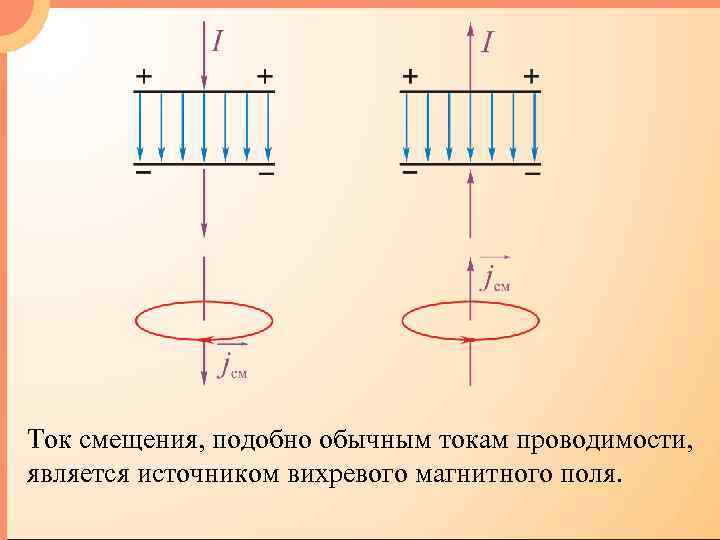Ток смещения, подобно обычным токам проводимости, является источником вихревого магнитного поля.

(10. 06) Циркуляция вектора Н напряженности магнитного поля по произвольному неподвижному замкнутому контуру L, мысленно проведенному в электромагнитном поле, равна алгебраической сумме макротоков и тока смещения сквозь поверхность, ограниченную этим контуром. (10. 07)

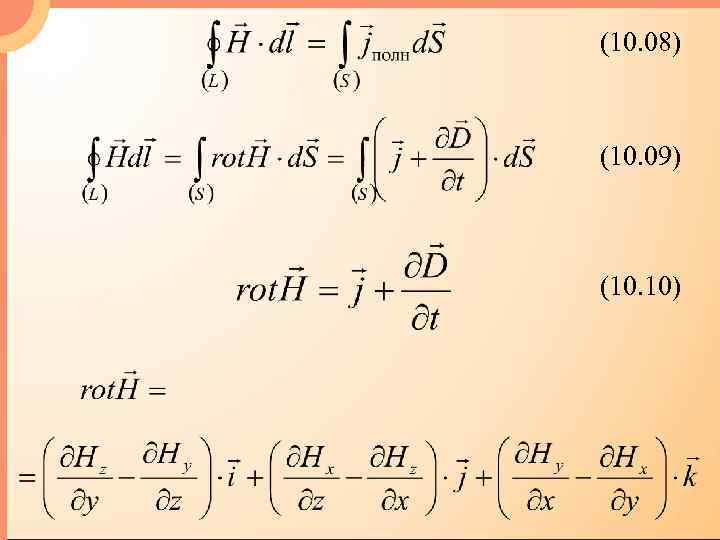(10. 08) (10. 09) (10. 10)

10. 4. Третье и четвертое уравнения Максвелла. Третье уравнение Максвелла – обобщение теоремы Гаусса для электростатического поля. (10. 11) Поток электрического смещения через произвольную неподвижную замкнутую поверхность, мысленно проведенную в электромагнитном поле, равен суммарному свободному заряду, который находится внутри области, ограниченной этой поверхностью.

(10. 12) Четвертое уравнение Максвелла – обобщение теоремы Гаусса для магнитного поля. (10. 13)

Магнитный поток через произвольную замкнутую поверхность, мысленно проведенную в электромагнитном поле, равен нулю. (10. 14)

10. 5. Система уравнений Максвелла. (10. 15) Материальные уравнения:

Стационарные поля:

Уравнения Максвелла инвариантны относительно преобразований Лоренца.