ФИЗИКА ч I МЕХАНИКА МЕХАНИКА Механика изучает

ФИЗИКА ч. I МЕХАНИКА

МЕХАНИКА Механика изучает мех. движение тел. Мех. движение – изменение положения тела относительно других тел. Для описания движения необходима система отсчёта: тело отсчёта, система координат, часы. 3

Основная задача механики –, определить положение тела в произвольный момент времени.

Используемые модели: материальная точка (МТ), абсолютно твердое тело. Материальная точка – тело, размерами и формой которого в данной задаче можно пренебречь. Массой – нельзя! Абсолютно твердое тело – такое тело, деформацией которого можно пренебречь.

Кинематика материальной точки Траектория – линия, по которой движется материальная точка. Положение точки можно задать: 1) с помощью координат х, y, z – координатный способ, 2) с помощью радиус –вектора - векторный способ, 3) заданием траектории и пути s. . Радиус-вектор – это вектор, проведенный из начала координат в данную точку траектории.

Радиус вектор Элементы кинематики 7

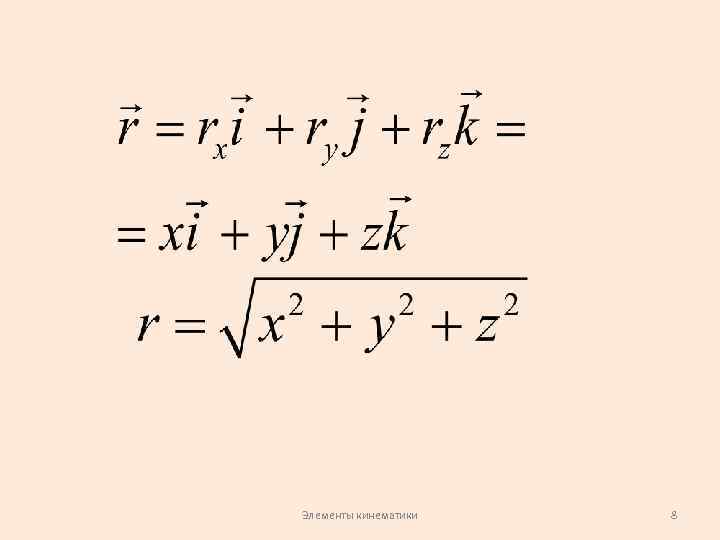Элементы кинематики 8

Путь и перемещение Элементы кинематики 9

Элементы кинематики 10

СКОРОСТЬ Средний вектор скорости Направлен по перемещению! Средняя путевая скорость (средний модуль скорости)

Вектор мгновенной скорости – это скорость в данный момент времени. , , где — проекции вектора скорости на оси координат. 12

модуль Т. к то -мгновенная путевая скорость Мгновенная скорость направлена по касательной к траектории.

УСКОРЕНИЕ Средний вектор ускорения Мгновенное ускорение Ускорение характеризует быстроту изменения вектора скорости со временем.

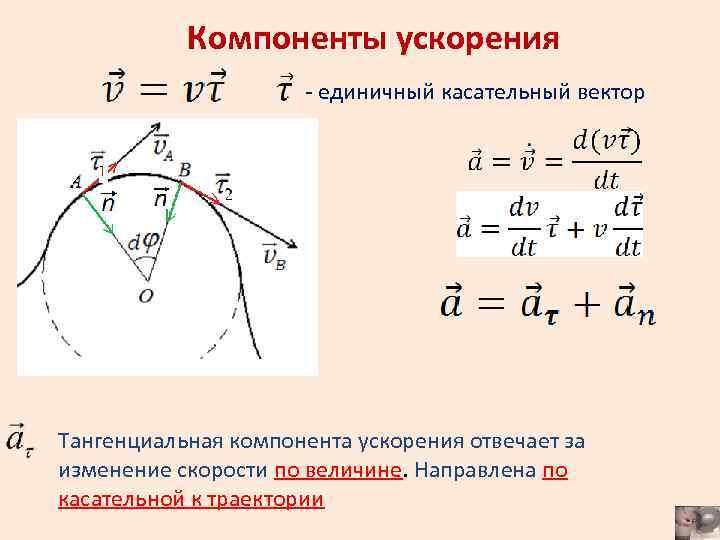Компоненты ускорения - единичный касательный вектор Тангенциальная компонента ускорения отвечает за изменение скорости по величине. Направлена по касательной к траектории

При движении по траектории единичный касательный вектор меняет свое направление. - в первый момент отсчета времени - во второй момент отсчета времени Совместим эти векторы началами. единичный вектор, перпендикулярный вектору скорости

Нормальная компонента ускорения отвечает за изменение скорости по направлению. Направлена к центру кривизны траектории.

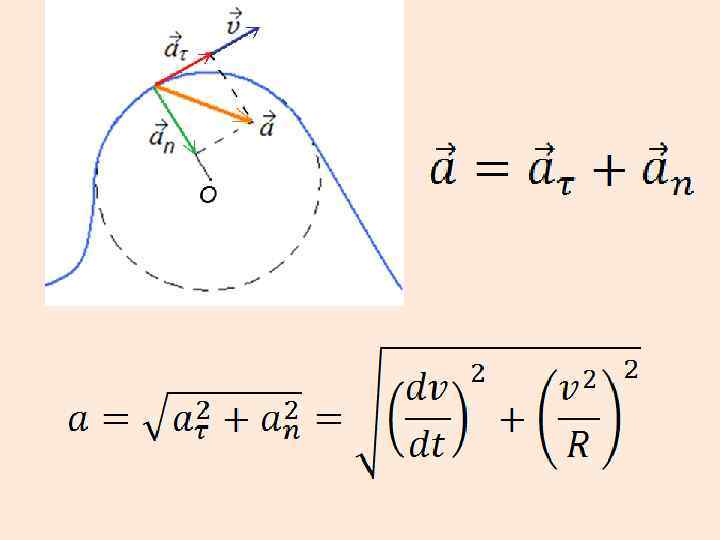
ВИДЫ ДВИЖЕНИЯ 1. Равнопеременное движение Равнопеременным называют движение с постоянным ускорением По определению (1) По определению подставим (1)

Кинематическое уравнение равнопеременного движения в векторной форме В траекторной форме Кинематическое уравнение движения по произвольной траектории с постоянной тангенциальной составляющей вектора ускорения (aτ =const) Элементы кинематики 20

В случае прямолинейного равноускоренного движения - движение равноускоренное - движение равнозамедленное (+) (-)

Равномерное прямолинейное движение Вектор мгновенной скорости остается постоянным не только по модулю, но и по направлению.

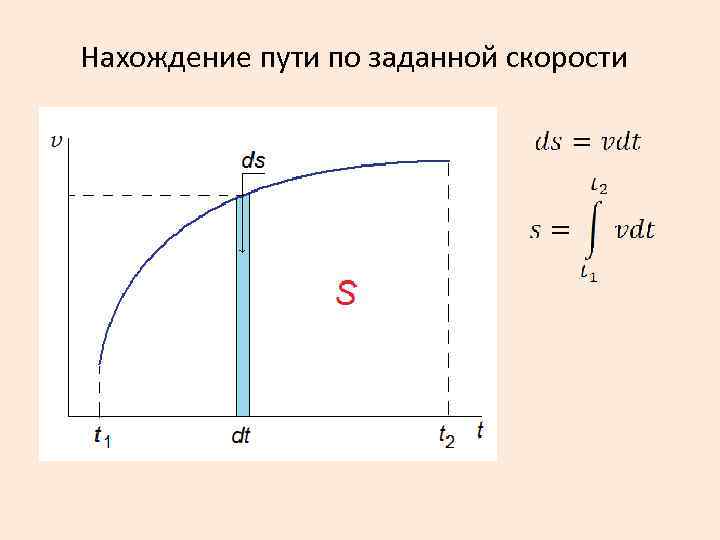Нахождение пути по заданной скорости

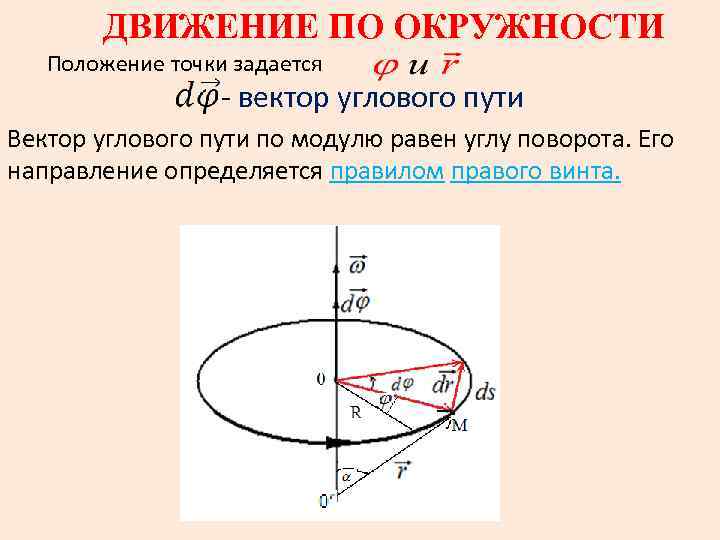ДВИЖЕНИЕ ПО ОКРУЖНОСТИ Положение точки задается - вектор углового пути Вектор углового пути по модулю равен углу поворота. Его направление определяется правилом правого винта.

Угловая скорость характеризует быстроту движения материальной точки по окружности. Угловое ускорение характеризует быстроту изменения угловой скорости со временем.

Векторы углового пути, угловой скорости, углового ускорения направлены вдоль оси вращения (это псевдовектора)! Если ω увеличивается, то Если ω уменьшается, то

Связь линейных и угловых характеристик движения Свяжем линейный и угловой пути Возьмем производную по времени Получим связь линейной и угловой скоростей

Векторное произведение векторов. a Примеры Направление вектора находят по правилу правого винта.

Скалярное произведение векторов. a Примеры

модуль тангенциального ускорения модуль нормального ускорения

Производная вектора. Показывает, как изменяется модуль вектора. Показывает, как изменяется направление вектора.

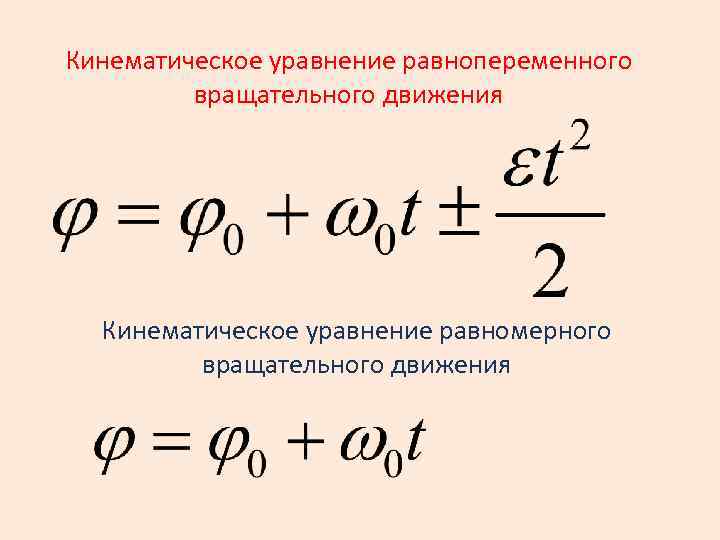Кинематическое уравнение равнопеременного вращательного движения Кинематическое уравнение равномерного вращательного движения

Характеристики равномерного вращения Период Т – время одного оборота. Частота вращения ν = числу оборотов в единицу времени. Найдем угловую скорость при равномерном вращении:

ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА Поступательное движение – все точки тела движутся одинаково. Любая прямая, связанная с телом, параллельна самой себе. Достаточно описать движение одной точки. Вращательное движение – точки тела движутся по окружностям, центры которых лежат на неподвижной прямой, называемой осью вращения.