ФИЗИКА АТОМНОГО ЯДРА И ЧАСТИЦ • • • • Программа курса 1. Введение. 2 Основные свойства атомных ядер 3. Радиоактивность 4. Нуклон - нуклонное взаимодействие и свойства ядерных сил 5. Модели атомных ядер 6. Ядерные реакции 7. Деление ядер 8. Сверхтяжёлые ядра и экспериментальные методы физики низких энергий 9. Взаимодействие ядерного излучения с веществом 10. Ядерные технологии 11. Частицы и взаимодействия 12. Фундаментальные частицы Стандартной модели. 13. Современные астрофизические представления 14. Эксперименты в физике высоких энергий 15. Космические лучи.
Литература Ø Б. С. Ишханов, И. М. Капитонов, Н. П. Юдин. "Частицы и атомные ядра“, М. , МГУ 2005. Ø Н. Г. Гончарова, Б. С. Ишханов, И. М. Капитонов, Э. И. Кэбин, М. Е. Степанов. "Физика ядра и частиц. Задачи с решениями", М. , Из-во УНЦДО, 2003. Ø "Субатомная физика. Вопросы. Задачи. Факты. " - под редакцией Б. С. Ишханова, изд-во МГУ, 1994. Ø К. Н. Мухин. "Экспериментальная ядерная физика" (в трех томах), М. , Энергоатомиздат. 1993. Ø http: //theory. asu. ru/~raikin/Students/IT_SE/nuclphys. sinp. msu. ru/npi. html ØИ. М. Капитонов, «Введение в Физику Ядра и Частиц", М. , Изд. Ком. Книгак, 2006. ØК. Н. Мухин. "Экспериментальная ядерная физика" (в трех томах), C. - Перербург, Изд-во “ЛАНЬ”. 2008.
2. Основные свойства атомных ядер • • Опыт Резерфорда. Размеры ядер. Ядро как совокупность протонов и нейтронов. Распределение заряда в ядре. Масса и энергия связи ядра. Стабильные и радиоактивные ядра. Квантовые характеристики ядерных состояний. • Спин ядра.
Открытие радиоактивности Флюоресценция – видимое свечение некоторых веществ в результате облучения их солнечным ультрафиолетом. А. Беккереля заинтересовал вопрос, имеется ли в спектре флюоресценции уранила сульфата калия рентгеновские лучи. Он помещал образец исходного соединения на фотопластинку, завернутую в черную непрозрачную для света бумагу и затем выставлял их на солнце. Беккерель получил положительный результат. Действительно, пластинки темнели. Однако, благодаря случайному стечению обстоятельств, он сделал для себя неожиданное открытие. В ожидании очередного солнечного дня он положил фотопластинки вместе с образцом урановой соли в ящик своего письменного стола. Через несколько дней он решил перед очередными опытами проверить качество пластинок и обнаружил на них отпечатки урановой соли. Пластинки почернели без всякого облучения на солнце. Беккерель предположил, и опыты это быстро подтвердили, что неизвестное излучение испускает уран. Это излучение происходит без всякого предварительного облучения на солнце. Так было открыто явление радиоактивности.
Открытие радиоактивности В 1899 году Эрнст Резерфорд открыл, что уранил сульфата калия испускает излучение трех различных типов. Он разделил их по проникающей способности и назвал a (альфа), b (бэта) и g (гамма) излучение по трем первым буквам греческого алфавита. a излучение может быть задержано листом бумаги. Позднее Резерфорд показал, что альфа излучение – это ядра атома гелия, 4 He. Бэта частицы впоследствии были идентифицированы как электроны, имеющие достаточно высокую скорость. Для того, чтобы затормозить большинство бэта частиц, испускаемых уранилом, требуется 6 мм алюминия. Для торможения гамма лучей необходимо несколько миллиметров свинца. Сейчас известно, что это высокоэнергичные фотоны. Альфа частицы и гамма лучи испускаются с определенной энергией, которая зависит от радиоактивного изотопа. Бэта частицы имеют сплошной спектр от нуля до определенной максимальной энергии, также зависящей от изотопа.
Атом Томсона В 1887 г. Д. Томсон, изучая характеристики газового разряда, показал, что катодные лучи, образующиеся в разрядной трубке, состоят из отрицательно заряженных частиц вещества. Отклоняя катодные лучи в электрических и магнитных полях, он определил отношение заряда к массе этих частиц. Он показал, что катодные лучи представляют собой поток более лёгких, чем атомы, частиц и не зависят от состава газа. Эти частицы были названы электронами. Открытие электрона и установление того факта, что все атомы содержат электроны, явилось важной информацией о внутреннем строении атома. В 1906 г. Томсон предложил модель, в которой электрически нейтральный атом состоит из положительно заряженного однородного шара, внутри которого в определенных равновесных положениях находится Z электронов. Так как электроны обладают отрицательными зарядами, а сами атомы являются электрически нейтральными системами, каждый атом должен содержать достаточное количество положительно заряженного вещества, чтобы скомпенсировать отрицательный заряд электрона. Размер атома ~10– 8 см. Модель Томсона просуществовала до 1911 г. , когда она была подвергнута серьезной проверке в экспериментах, выполненных Э. Резерфордом и его двумя учениками Гейгером и Марсденом.
Открытие атомного ядра • 1904 г. Дж. Томсон, атом - нейтральная система - из заряженного шара с зарядом +Ze, внутри Z отрицательно заряженных электронов. Размер атома ~10 -8 см. • 1911 г. Э. Резерфорд, положительно заряженное атомное ядро с радиусом < 10 -12 см и электронная оболочка с радиусом ~10 -8 см. 99. 98% массы в ядре.
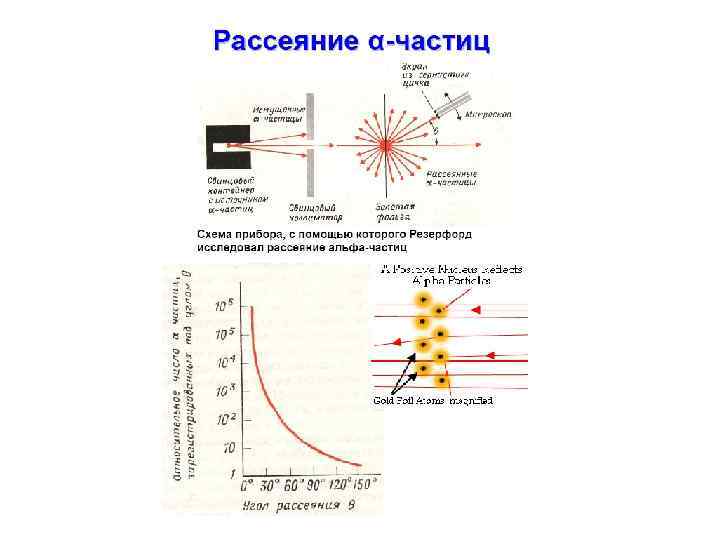
Резерфорд открывает атомное ядро Параллельно с развитием идей квантовой теории развивались представления о строении материи. Одна из первых моделей атома была предложена в 1904 году Дж. Томсоном. Согласно модели Дж. Томсона атом представлял собой нейтральную систему, состоящую из заряженного шара с зарядом +Ze, внутри которого в определенных равновесных положениях находятся Z отрицательно заряженных электронов. Размер атома ~10 -8 см. Прямые экспериментальные исследования строения атома были выполнены в 1911 году Э. Резерфордом, который изучал рассеяние частиц при прохождении через тонкую золотую фольгу. Дифференциальное сечение упругого рассеяния нерелятивистской заряженной частицы в кулоновском поле ядра-мишени описывается формулой Резерфорда (1) где Z 1 и Z 2 - заряды налетающей частицы и ядра-мишени, e - элементарный заряд, T - кинетическая энергия налетающей частицы, - угол рассеяния.
Резерфорд открывает атомное ядро Формула Резерфорда получена при следующих предположениях. • Ядро и α-частица точечные (Rядра = 0, Rα = 0). • Масса ядра mядра много больше массы налетающей α-частицы mα (mядра >> mα). • Спин ядра и спин α -частицы равны 0 (sα = sядра = 0). • Магнитные моменты ядра и α -частицы равны 0 (µα = µядра= 0). • Механизм реакции - упругое рассеяние на ядре. • Потенциал рассеяния имеет вид Z 1 Z 2 e 2/R.
Резерфорд открывает атомное ядро Рис. 1. Рассеяние α-частицы в кулоновском поле ядра
Резерфорд открывает атомное ядро Угловое распределение α - частиц, рассеянных на золоте, свидетельствовало о том, что положительный заряд атома сосредоточен в пространственной области размером меньше 10 -12 см. Это явилось основанием для планетарной модели атома Резерфорда, согласно которой атом состоит из тяжелого положительно заряженного атомного ядра с радиусом меньше 10 -12 см и расположенным вокруг него облаком отрицательно заряженных электронов. Размер атома определяется размерами его электронной оболочки и составляет ~10 -8 см, что в десятки тысяч раз превышает размер атомного ядра. Несмотря на то, что атомное ядро занимает лишь небольшую часть объема атома в нем сосредоточено 99, 98% его массы. Расстояние наибольшего rmin сближения α - частицы с положительно заряженным ядром зависит от ее кинетической энергии T, заряда ядра Z и величины прицельного параметра b. (2)
Резерфорд открывает атомное ядро Из соотношения (2) следует, что с уменьшением прицельного параметра b, увеличивается угол рассеяния . Это происходит потому, что частица ближе подходит к рассеивающему центру и испытывает большее действие рассеивающего кулоновского потенциала V~1/r. Из того факта, что упругое рассеяние α -частиц с энергией 5. 5 Мэ. В хорошо описывалось формулой (1), следовало, что размер атомного ядра меньше 5· 10 -12 см. Уточнить размеры атомных ядер удалось увеличивая энергию α частиц, что позволило уменьшить величину расстояния наибольшего сближения α -частицы с ядром. На рис. 2 показана зависимость отношения экспериментального сечения к сечению кулоновского рассеяния от угла рассеяния для упругого рассеяния α -частиц с энергией 22 Мэ. В на ядрах свинца. Отклонение экспериментального сечения при углах > 900 от формулы Резерфорда (1) означает, что прицельный параметр b сравним с размерами ядра. С помощью формулы (2), подставив в нее θ = 900, можно получить оценку радиуса ядра свинца - (56)· 10 -13 см = 5 -6 Фм. Формула (1) применима в случае, если расстояние наибольшего сближения между налетающей частицей и рассеивающим ядром превышает радиус ядра и, если можно пренебречь экранировкой ядра электронами.
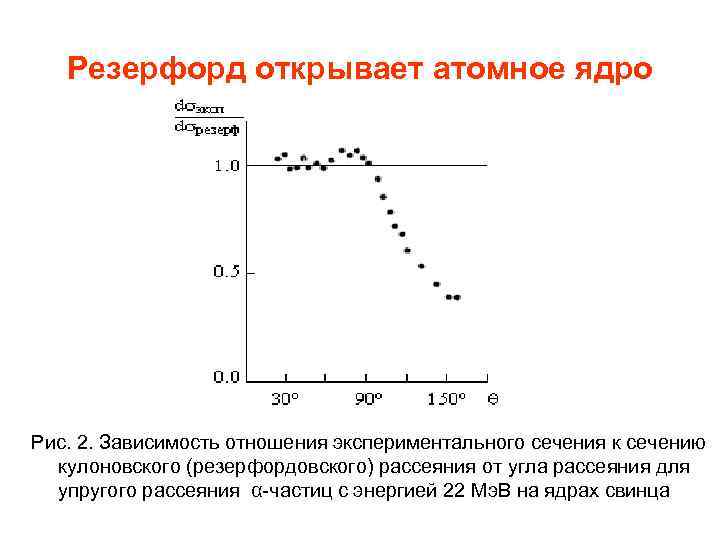Резерфорд открывает атомное ядро Рис. 2. Зависимость отношения экспериментального сечения к сечению кулоновского (резерфордовского) рассеяния от угла рассеяния для упругого рассеяния α-частиц с энергией 22 Мэ. В на ядрах свинца
Резерфорд открывает атомное ядро Наблюдаемое при θ > 900 падение дифференциального сечения по сравнению с предсказаниями формулы Резерфорда обусловлено тем, что при сближении налетающей α -частицы и ядра свинца до расстояния < 6 Фм в действие вступают силы отличные от кулоновских - ядерные силы. Предложенная Э. Резерфордом модель атома сыграла решающую роль в развитии квантовой механики. Дело в том, что на основе классической физики невозможно было объяснить наблюдаемую на опыте устойчивость атома. Вращающиеся на орбите электроны, согласно классической физике, должны были излучать энергию и, потеряв ее, упасть на атомное ядро. Поскольку такие явления как фотоэффект и явление дифракции электронов удалось объяснить с помощью квантовых представлений, вполне разумно казалось попытаться с помощью такого подхода объяснить и устойчивость электронных орбит атома.
Резерфорд открывает атомное ядро В 1913 году Н. Бор предложил новую квантовую теорию орбит. Согласно этой теории электрон может вращаться вокруг ядра неопределенно долго, не излучая энергию, если на его орбите укладывается целое число длин волн де Бройля. Таким образом устойчивые орбиты в атоме это орбиты, радиусы которых rn определяются соотношением rn = n 2 h 2/Zmee, что соответствует определенным энергетическим уровням атома En = - Z 2 e 4 me/2 n 2 h 2. Атом может перейти из одного состояния в другое, испустив квант энергии - фотон h = E i - Ek, где Ei и Ek - энергии уровней, между которыми происходит переход.
Pазмеры и структура ядер • Некоторое время атомное ядро и электроны считались элементарными составляющими вещества. Первое указание на существование атомного ядра связано с открытием в 1896 году А. Беккерелем радиоактивности. Это произошло задолго до того, как Резерфорд экспериментально доказал его существование. Оказалось, что некоторые минералы естественного происхождения самопроизвольно испускают излучение неизвестной природы. По прошествии нескольких лет было показано, что неизвестное излучение состоит из частиц трех различных видов, сильно отличающихся друг от друга: • Нейтрально заряженных частиц - фотонов. • Отрицательно заряженных частиц- электронов. • Положительно заряженных частиц. Вначале считалось, что обнаруженные излучения испускаются атомом, и лишь впоследствии стало ясно, что их источником является атомное ядро. Явление самопроизвольного распада атомных ядер стало называться радиоактивностью. Выдающуюся роль в понимании природы радиоактивного распада сыграли работы Пьера и Марии Кюри. Изучая треки образующихся при радиоактивном распаде положительно заряженных частиц в электрическом поле, Э. Резерфорд показал, что это частицы с массой атома гелия и зарядом +2 e. В 1919 году Ф. Астон построил первый масс-спектрограф, с помощью которого были получены точные значения масс атомных ядер. Было доказано, что положительно заряженные частицы, обнаруженные при радиоактивном распаде ядер, являются ядрами атома гелия. Эти частицы были названы α-частицами.
Pазмеры и структура ядер • Первая ядерная реакция В 1919 г. , продолжая эксперименты по рассеянию α-частиц на различных мишенях, Э. Резерфорд обнаружил, что при бомбардировке ядер азота α -частицами из него вылетают положительно заряженные частицы. Величина заряда этих частиц по абсолютной величине была равна величине заряда электрона, но противоположна по знаку. Масса частицы была почти в 2000 раз больше массы электрона. Повторение опыта на других мишенях показало, что положительно заряженные частицы вылетают и из других атомных ядер. Обнаруженные частицы были названы протонами. Ядерная реакция, в которой впервые были обнаружены протоны, записывается в виде 14 N + α → 17 O + p Уже первый взгляд на написанную реакцию свидетельствует о том, что Э. Резерфорду удалось осуществить то, что в течение многих веков пытались сделать алхимики - превратить одно вещество в другое. Ядро азота превращалось в ядро кислорода. Это была первая ядерная реакция, осуществленная искусственно в лабораторных условиях. В то же время стало ясно, что протоны следует считать элементарными частицами, входящими в состав атомного ядра.
Pазмеры и структура ядер Из чего состоит атомное ядро? Измерения масс атомов с помощью масс-спектрографа Ф. Астона показали, что массы всех исследованных атомов с точностью ~10% пропорциональны массе протона - M ~ Amp, где A принимает только целочисленные значения. Этот факт послужил основанием для создания протон-электронной модели атомного ядра. В этой модели предполагалось, что атомное ядро состоит из A протонов и (A-Z) электронов. В этой модели легко объяснялись обнаруженная Астоном пропорциональность массы атомного ядра числу A и величина заряда атомного ядра. Однако, по мере накопления экспериментальных данных по массам атомных ядер, магнитным моментам и спинам атомных ядер, протон-электронная модель ядра начала сталкиваться с трудностями в объяснении экспериментальных данных. Тем не менее, протон - электронная модель ядра продержалась вплоть до 1932 года. Простейшая модель α-распада была предложена в 1928 году Г. Гамовым и независимо от него Г. Герни и Э. Кондоном. В этой модели предполагалось, что α частица постоянно существует в ядре. Вероятность α -распада в основном определяется вероятностью прохождения α -частиц через кулоновский потенциальный барьер (рис. 3. ) • Рис. 3. Потенциальная энергия α-частицы
Pазмеры и структура ядер В рамках этой модели удалось объяснить сильную зависимость вероятности α -распада от энергии. В 1930 -1932 гг. разыгрались полные драматизма события. Продолжая начатые Резерфордом эксперименты по облучению тонких фольг из бериллия α -частицами, В. Боте и Г. Беккер обнаружили сильно проникающее излучение, состоящее из нейтральных частиц. Первоначально выдвинутая гипотеза о том, что это фотоны высоких энергий, не выдержала проверки. Лишь в 1932 г. английский физик Д. Чедвик показал, что это новая, до сих пор неизвестная нейтральная частица с массой, приблизительно равной массе протона. Обнаруженная частица была названа нейтроном. Сразу после открытия нейтрона Д. Иваненко и В. Гейзенберг независимо выдвинули гипотезу, что атомное ядро состоит из нейтронов и протонов. Эта модель выдержала испытания временем и, как показывают экспериментальные наблюдения, в обычных условиях отклонения от протонно-нейтронной модели, связанные с внутренней структурой нуклонов, невелики. Протоны и нейтроны в атомном ядре связаны особыми силами, для которых характерна большая величина и малый радиус действия ~10 -13 см. Ядерные силы существенно превосходят силы электростатического кулоновского отталкивания протонов и обуславливают большую плотность вещества ядра ~1014 г/см 3. Этот новый тип взаимодействия, связывающий нейтроны и протоны, назвали ядерным или сильным взаимодействием. Эти два названия долгое время считали синонимами. Сегодня мы знаем: сильное взаимодействие связывает кварки внутри нуклона, а ядерное взаимодействие, связывающее нейтроны и протоны, является следствием сильного взаимодействия.
Pазмеры и структура ядер Ядерное взаимодействие меняет свойства нуклонов. Так, например, свободный нейтрон, являясь нестабильной частицей, внутри ядра может стать стабильным. По отношению к сильному взаимодействию протон и нейтрон имеют одинаковые свойства. Это привело к открытию новой симметрии - изотопической инвариантности сильных взаимодействий. Была введена новая квантовая характеристика - изоспин. Протон и нейтрон образуют изотопический дублет (T = 1/2) и могут рассматриваться как два квантовых состояния одной частицы - нуклона с разными проекциями изоспина p |T = 1/2, Tz = +1/2|, n |T = 1/2, Tz = -1/2|. С помощью изотопической инвариантности сильных взаимодействий в дальнейшем удалось предсказать массы и электрические заряды некоторых новых элементарных частиц. Протоны и нейтроны образуют атомные ядра всех химических элементов. Число протонов в ядре определяет атомный номер элемента и, следовательно, его место в периодической системе элементов Менделеева.
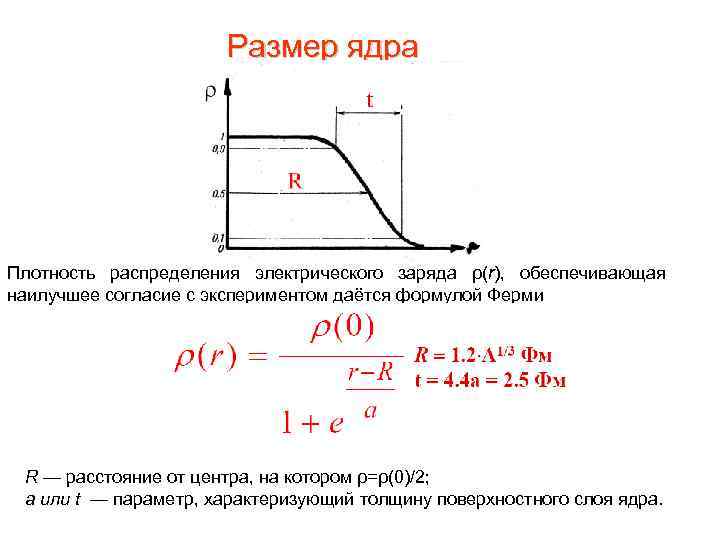Размер ядра Плотность распределения электрического заряда ρ(r), обеспечивающая наилучшее согласие с экспериментом даётся формулой Ферми R — расстояние от центра, на котором ρ=ρ(0)/2; а или t — параметр, характеризующий толщину поверхностного слоя ядра.
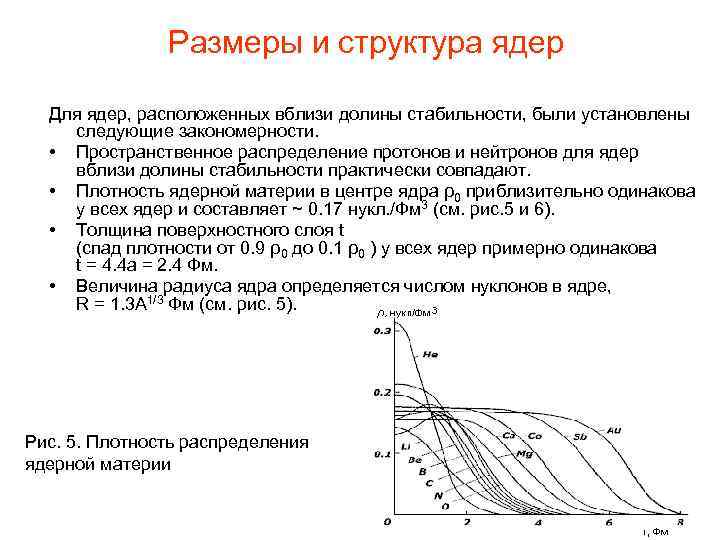Pазмеры и структура ядер Для ядер, расположенных вблизи долины стабильности, были установлены следующие закономерности. • Пространственное распределение протонов и нейтронов для ядер вблизи долины стабильности практически совпадают. • Плотность ядерной материи в центре ядра ρ0 приблизительно одинакова у всех ядер и составляет ~ 0. 17 нукл. /Фм 3 (см. рис. 5 и 6). • Толщина поверхностного слоя t (спад плотности от 0. 9 ρ0 до 0. 1 ρ0 ) у всех ядер примерно одинакова t = 4. 4 a = 2. 4 Фм. • Величина радиуса ядра определяется числом нуклонов в ядре, R = 1. 3 A 1/3 Фм (см. рис. 5). Рис. 5. Плотность распределения ядерной материи
Размер ядра Радиальное распределение плотности заряда в различных ядрах
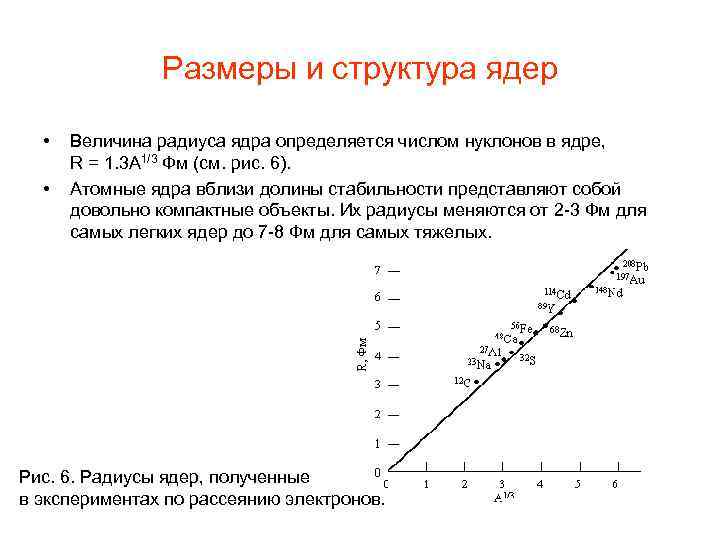Pазмеры и структура ядер • • Величина радиуса ядра определяется числом нуклонов в ядре, R = 1. 3 A 1/3 Фм (см. рис. 6). Атомные ядра вблизи долины стабильности представляют собой довольно компактные объекты. Их радиусы меняются от 2 -3 Фм для самых легких ядер до 7 -8 Фм для самых тяжелых. Рис. 6. Радиусы ядер, полученные в экспериментах по рассеянию электронов.
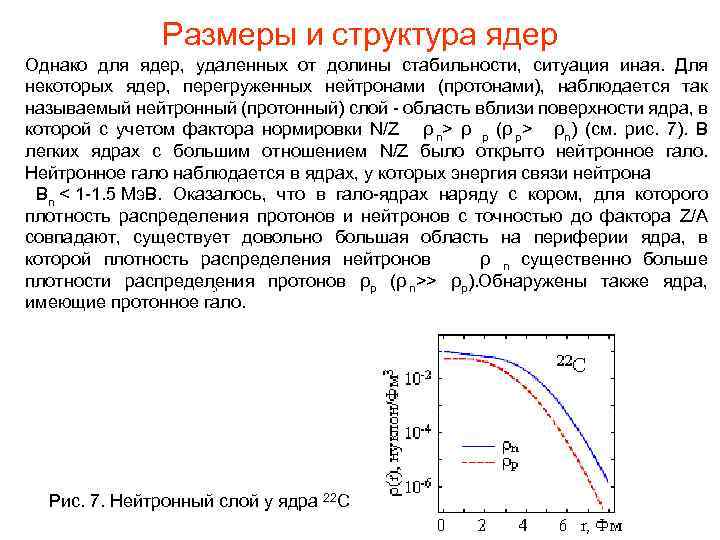Pазмеры и структура ядер Однако для ядер, удаленных от долины стабильности, ситуация иная. Для некоторых ядер, перегруженных нейтронами (протонами), наблюдается так называемый нейтронный (протонный) слой - область вблизи поверхности ядра, в которой с учетом фактора нормировки N/Z ρ n> ρ p (ρ p> ρn) (см. рис. 7). В легких ядрах с большим отношением N/Z было открыто нейтронное гало. Нейтронное гало наблюдается в ядрах, у которых энергия связи нейтрона Bn < 1 -1. 5 Мэ. В. Оказалось, что в гало-ядрах наряду с кором, для которого плотность распределения протонов и нейтронов с точностью до фактора Z/A совпадают, существует довольно большая область на периферии ядра, в которой плотность распределения нейтронов ρ n существенно больше плотности распределения протонов ρp (ρ n>> ρp). Обнаружены также ядра, имеющие протонное гало. Рис. 7. Нейтронный слой у ядра 22 С
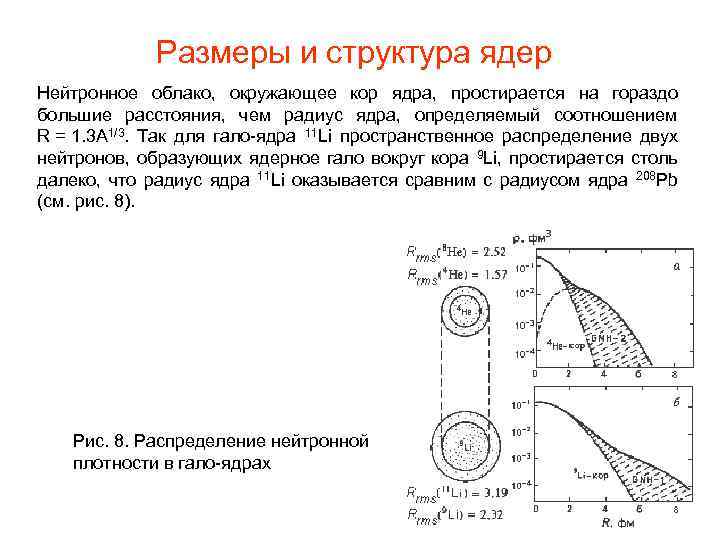Pазмеры и структура ядер Нейтронное облако, окружающее кор ядра, простирается на гораздо большие расстояния, чем радиус ядра, определяемый соотношением R = 1. 3 A 1/3. Так для гало-ядра 11 Li пространственное распределение двух нейтронов, образующих ядерное гало вокруг кора 9 Li, простирается столь далеко, что радиус ядра 11 Li оказывается сравним с радиусом ядра 208 Pb (см. рис. 8). Рис. 8. Распределение нейтронной плотности в гало-ядрах
Распределение заряда в ядре • • Распределение заряда и массы в атомных ядрах исследуется в экспериментах по упругому рассеянию на ядрах альфа-частиц (исторически это первые эксперименты Резерфорда), электронов и протонов. Выяснилось, что как плотность распределения заряда, так и плотность распределения массы ядра приближенно выражаются распределением Ферми: Величину R называют радиусом ядра. Отметим, что поскольку распределение плотности заряда и массы близки, но не совпадают друг с другом, отличаются также и зарядовый и массовый радиусы. В приближенных расчетах можно считать эти величины совпадающими и полагать, что радиус ядра R ~ r 0 A 1/3.
Распределение заряда в ядре • Это одновременно означает независимость средней плотности ядра от массового числа. Действительно, оценим плотность ядра с числом нуклонов А: Полученные результаты для плотности и радиуса эквивалентны утверждению о полной несжимаемости ядерной материи. В большинстве приближенных расчетов это утверждение можно использовать, однако отклонение от него хорошо видно на примере распределения среднеквадратичного радиуса распределения заряда для разных ядер. На рис. 9 показаны результаты исследований среднеквадратичного зарядового радиуса для некоторых ядер, полученные в экспериментах по неупругому рассеянию электронов на ядрах. Следует обратить внимание на отклонение величины зарядового радиуса от формулы. Например, зарядовый радиус ядра 48 Са меньше, чем зарядовый радиус ядра 40 Са. Для изотопов титана рост А ведет к уменьшению зарядового радиуса. Эти эффекты нашли качественное объяснение в модели ядерных оболочек.
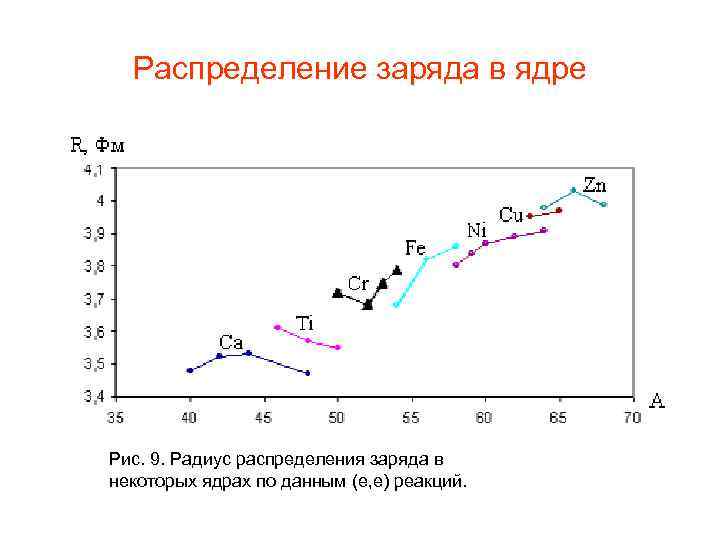Распределение заряда в ядре Рис. 9. Радиус распределения заряда в некоторых ядрах по данным (e, e) реакций.
N-Z диаграмма атомных ядер Атомные ядра представляют собой связанные квантовые системы фермионов. Свойства атомных ядер определяются совместным действием сильного, электромагнитного и слабого взаимодействий. В настоящее время обнаружено ~ 3000 атомных ядер, представляющих собой различные сочетания чисел протонов Z и нейтронов N. По существующим оценкам число атомных ядер может составлять ~ 6500. На рисунке показана N-Z диаграмма атомных ядер. Черными точками показаны стабильные ядра. Область расположения стабильных ядер обычно называют долиной стабильности. Для ядер долины стабильности характерно следующее отношение числа нейтронов к числу протонов: N/Z = 0. 98 + 0. 015·A 2/3, где A= N + Z – массовое число. Легкие стабильные ядра (А < 40) имеют приблизительно равные числа нейтронов и протонов. В области более тяжелых ядер отношение числа нейтронов к числу протонов начинает возрастать и достигает величины 1. 6 в районе А=250. Это изменение легко понять, если учесть короткодействующий характер ядерных сил и возрастающую роль кулоновского взаимодействия протонов с ростом А. Тяжелые ядра оказываются энергетически более устойчивыми, если содержат большее число нейтронов N по сравнению с числом протонов Z. Наиболее тяжелыми стабильными ядрами являются изотопы свинца (Z = 82) и висмут (Z = 83). .
N-Z диаграмма атомных ядер
N-Z диаграмма атомных ядер • Пунктирная линия очерчивает область возможного существования атомных ядер. Связанное состояние ядра определяется как состояние, стабильное относительно испускания нейтронов или протонов, т. е. считается, что атомное ядро существует, если оно не испускает нуклоны из основного состояния. Линия Bp = 0 (Bp - энергия отделения протона) ограничивает область существования атомных ядер слева (proton drip-line). Линия Bn = 0 (Bn - энергия отделения нейтрона) - справа (neutron drip-line). Вне этих границ атомные ядра существовать не могут, так как они распадаются за характерное ядерное время (~ 10 -23 c) с испусканием одного или нескольких нуклонов. Если среднее время жизни ядра < 10 -22 с, обычно считается, что ядра не существуют. Характерные времена жизни для радиоактивных ядер > 10 -14 c. Времена жизни ядер, обусловленные испусканием нуклонов 10 -23 с < τ <10 -20 c. Ядра, имеющие такие времена жизни, обычно наблюдаются в виде резонансов в сечениях ядерных реакций.
N-Z диаграмма атомных ядер Различные комбинации чисел протонов Z и нейтронов N соответствуют различным атомным ядрам. Атомные ядра существуют (т. е. их время жизни τ > 10 -23 c) в довольно узком диапазоне изменений чисел Z и N. Все атомные ядра делятся на две большие группы —стабильные и радиоактивные. Стабильные ядра группируются вблизи долины стабильности: С левой стороны от стабильных ядер находятся ядра, перегруженные протонами (протоноизбыточные ядра), справа – ядра, перегруженные нейтронами (нейтроноизбыточные ядра). Обнаруженное в настоящее время число радиоактивных ядер около 3, 5 тысяч. Считается, что всего их должно быть 7 – 7, 5 тысяч. Протоноизбыточные ядра являются радиоактивными и превращаются в стабильные в основном в результате β+ - распадов. Нейтроноизбыточные ядра также являются радиоактивными и превращаются в стабильные в результате β− - распадов, с превращением нейтрона ядра в протон. Самыми тяжелыми стабильными изотопами являются изотопы свинца (Z=82) и висмута (Z=83). В тяжелых ядрах происходят такж α-распад и спонтанное деление, которые становятся их основными каналами распада.
N-Z диаграмма атомных ядер • Рассчитать границы нуклонной стабильности довольно сложно, т. к. точность, с которой оцениваются энергии связи ядер (несколько сотен кэ. В), недостаточна для того, чтобы определить будет ли ядро радиоактивным или оно будет распадаться с испусканием нуклона. Поэтому точность предсказания границы существования атомных ядер для отдельных элементов может составлять 4 -5 единиц по A. В первую очередь это относится к границе нейтронной стабильности. В правом верхнем углу N – Z диаграммы расположена интенсивно исследуемая в настоящее время область сверхтяжелых атомных ядер. Открытие и исследование сверхтяжелых атомных ядер с Z = 109 -118 показывает, что в этой области ядер существенную роль в повышении их стабильности играют ядерные оболочки. Достаточно хорошее согласие теоретических расчетов с полученными в последнее время экспериментальными данными позволяет прогнозировать существование острова стабильности в районе Z = 110 -114 и N = 178184. Ядра на острове стабильности должны иметь повышенную устойчивость по отношению к альфа и бета-распаду и спонтанному делению. Теоретические оценки показывают, что времена жизни ядер, расположенных в центре острова стабильности могут составлять ~105 лет. Трудность проникновения на остров стабильности связана с тем, что нет комбинации соответствующих ядер, использование которых в качестве мишени и налетающей частицы позволили бы попасть в центр острова стабильности.
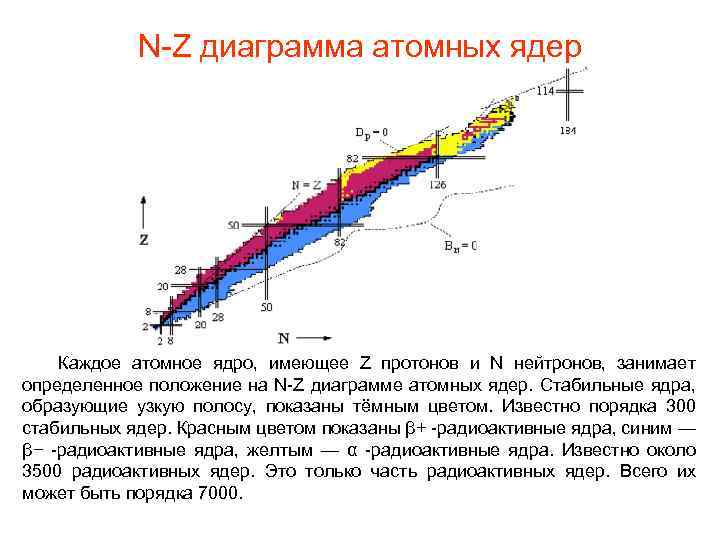N-Z диаграмма атомных ядер Каждое атомное ядро, имеющее Z протонов и N нейтронов, занимает определенное положение на N-Z диаграмме атомных ядер. Стабильные ядра, образующие узкую полосу, показаны тёмным цветом. Известно порядка 300 стабильных ядер. Красным цветом показаны β+ -радиоактивные ядра, синим — β− -радиоактивные ядра, желтым — α -радиоактивные ядра. Известно около 3500 радиоактивных ядер. Это только часть радиоактивных ядер. Всего их может быть порядка 7000.
N-Z диаграмма атомных ядер Стабильные ядра - известно около 300 стабильных ядер Радиоактивные ядра - известно около 3000 радиоактивных ядер Изотопы Ядра с одинаковым Z Изобары Ядра с одинаковым A Каждому ядру соответствует определённое положение на N, Z диаграмме. Стабильные и долгоживущие ядра образуют узкую полосу, называемую линией или долиной стабильности. Легкие стабильные ядра (А < 40) имеют приблизительно равные числа нейтронов и протонов. В области более тяжелых ядер отношение числа нейтронов к числу протонов начинает возрастать и достигает величины 1. 6 в районе А = 250. Это изменение отношения N/Z обусловлен короткодействующим характером ядерных сил и возрастающей ролью кулоновского отталкивания протонов с ростом А. Тяжелые ядра оказываются энергетически более устойчивыми, если содержат большее число нейтронов N по сравнению с числом протонов Z. Наиболее тяжелыми стабильными ядрами являются изотопы свинца (Z = 82) и висмута (Z = 83). Для ядер долины стабильности характерно следующее отношение числа нейтронов к числу протонов:
Масса ядра Основные методы определения масс ядер. • Метод магнитного анализа. Магнитная жесткость Bρ, масса ядра M, его скорость V и заряд Q связаны соотношением B - напряженность магнитного поля, ρ - радиус поворота иона в магнитном поле. • Метод времени пролета. Масса иона определяется из соотношения • Измерение циклотронной частоты. Частота ω иона, вращающегося в постоянном магнитном поле B, связана с его массой M и зарядом Q соотношением
Масса ядра • Измерение энергии реакции Q. В двухчастичной реакции A+a→B+b массы ядер связаны соотношением Если известны массы трех частиц, то масса четвертой частицы определяется по результатам измерения энергии реакции Q. • Измерение α-спектров. Для α-радиоактивных ядер масса ядра определяется из анализа энергетических спектров α-частиц. • Измерение энергии β-распада Qβ. Масса ядра, испытывающего β-распад, определяется из соотношения
Масса и энергия связи ядра • • Масса ядра измеряется в атомных единицах массы (а. е. м). За одну атомную единицу массы принимается 1/12 часть массы нейтрального атома углерода 12 С: 1 а. е. м = 1. 6606 10 -27 кг. А. е. м. выражается через энергетические единицы: 1 а. е. м = 1. 510 -3 эрг = 1. 510 -10 Дж = 931. 49 Мэ. В Масса ядра всегда меньше суммы масс составляющих его нуклонов. Энергия связи ядра Eсв(A, Z) это минимальная энергия, необходимая, чтобы развалить ядро на отдельные, составляющие его нуклоны. Есв(A, Z) = [Z mp + (A - Z)mn - M(A, Z)]c 2, где Z - число протонов, ( A - Z) - число нейтронов, mp - масса протона, mn - масса нейтрона, М(A, Z) - масса ядра с массовым числом А и зарядом Z. Энергия связи ядра, выраженная через массу атома Mат, имеет вид: • Есв(A, Z) = [Zm. H + (A - Z)mn - Mат(A, Z) - Zme)]c 2 , • где m. H - масса атома водорода, me - масса электрона
Масса и энергия связи ядра • • Энергии связи и массы ядер Масса стабильных ядер меньше суммы масс входящих в ядро нуклонов, - разность этих величин и определяет энергию связи ядра Eсв (binding energy ): • Eсв(A, Z) = Zmp + (A - Z)mn - MN(A, Z). • Формула является приближенной – в ней опущены энергии связи электронов в атомах. Однако поскольку энергии связи нуклонов в ядре на 5 – 6 порядков превышают энергии связи электронов в атомах, это приближение не скажется на точности дальнейших расчетов энергий связи ядер. • • В следующей формуле MN - масса ядра. В таблицах масс приводятся не массы ядер, а массы нейтральных атомов, либо величины, с ними связанные. Значения “избытков масс” Δ = M - A, где М – масса нейтрального атома в Мэ. В Величина А представляет собой в данном случае произведение числа нуклонов на значение единицы массы в Мэ. В. Таким образом, величины приводятся в единицах Мэ. В, что очень удобно для проведения расчетов. • • M(A, Z) = MN(A, Z) + Zme; Δ(A, Z) = M(A, Z) - A.
Масса и энергия связи ядра • Eсв(A, Z) = ZM(1 H) + (A - Z)mn - M(A, Z) = Z Δ(1 H) + (A - Z) Δ n - Δ(A, Z) Распределение удельных энергий связи ε = Eсв/A как функция числа нуклонов А является наиболее важным для приложений экспериментальным результатом физики ядра (см. рис. ) . Экспериментально установленное распределение удельных энергий связи ядер по значениям чисел нуклонов в ядре А имеет следующие характерные черты В широкой области ядер удельная энергия связи очень слабо зависит от А; для ядер с малыми А удельная энергия имеет “спад”. Для тяжелых ядер средняя удельная энергия связи меньше, чем для средних, причем с ростом А наблюдается снижение ее величины.
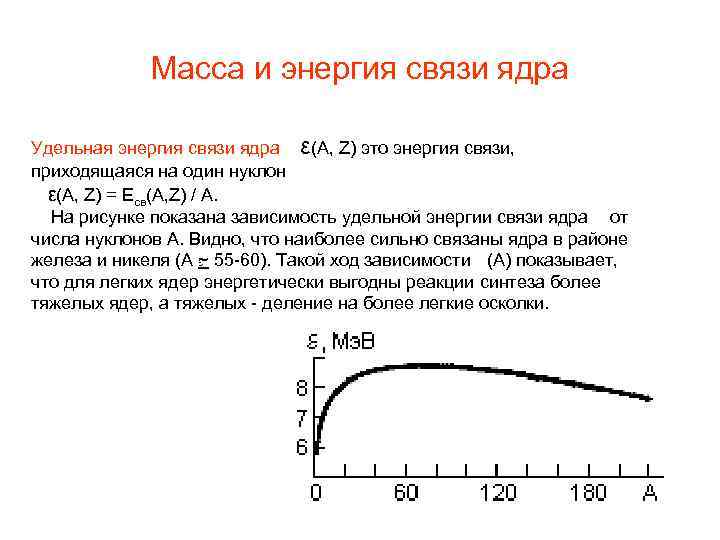Масса и энергия связи ядра Удельная энергия связи ядра ε(A, Z) это энергия связи, приходящаяся на один нуклон ε(A, Z) = Eсв(A, Z) / A. На рисунке показана зависимость удельной энергии связи ядра от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A ~ 55 -60). Такой ход зависимости (A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а тяжелых - деление на более легкие осколки.
Масса и энергия связи ядра • Экспериментально установленное распределение удельных энергий связи ядер по значениям чисел нуклонов в ядре А имеет следующие характерные черты: В широкой области ядер удельная энергия связи очень слабо зависит от А; для ядер с малыми А удельная энергия имеет “спад”. Для тяжелых ядер средняя удельная энергия связи меньше, чем для средних, причем с ростом А наблюдается снижение ее величины. Для ядер с Z = N удельная энергия выше, чем для других ядер с тем же значением А. Четно-четные (по Z и N) ядра имеют в среднем большие значения , чем нечетно-четные, а нечетно-нечетные – меньшие. Теоретическое объяснение этого распределения дает модель заряженной жидкой капли и соответствующая этой модели формула Вайцзеккера.
Масса и энергия связи ядра • Первая из перечисленных (и главная) особенность распределения удельных энергий связи ядер – следствие насыщения ядерных сил. Вторая связана с тем, что связи нуклонов, находящихся на поверхности ядра, с другими нуклонами ядра не полностью насыщены. Чем больший процент нуклонов находится на поверхности ядра, тем больше “убыль” энергии насыщения. (Этими особенностями ядерные силы оказываются подобны силам, действующим между молекулами жидкости). Третья особенность распределения удельной энергии связи объясняется тем, что протоны ядер участвуют не только в сильном (ядерном), но и в электромагнитном взаимодействии. Чем больше протонов, тем выше энергия кулоновского отталкивания. Четвертая и пятая особенности распределения – следствия оболочечной структуры ядра и симметрий, связанных с реализацией в ядре принципа Паули. Учет всех перечисленных свойств приводит к полуэмпирической формуле Вайцзеккера, или модели заряженной жидкой капли:
Энергия связи ядра Объемная энергия Если пренебречь быстрым уменьшением удельной энергии связи в легчайших ядрах и медленным в тяжелых, можно считать, что в первом приближении удельная энергия связи для большинства ядер остается постоянной. Поэтому энергия связи большинства ядер приближенно пропорциональна числу нуклонов: α − коэффициент пропорциональности. Это далеко идущее утверждение о линейной зависимости энергии связи от А, означает, во-первых, что ядерные силы, удерживающие нуклоны вместе, обладают свойством насыщения, при котором каждый нуклон имеет только одну связь, с помощью которой он может взаимодействовать с другими нуклонами.
Энергия связи ядра Поверхностная энергия Существование поверхности должно уменьшать энергию связи, так как связи нуклонов вблизи поверхности насыщаются меньше, чем внутри ядра. Поверхностная энергия тем больше, чем больше поверхность ядра, и записывается в виде
Энергия связи ядра Кулоновская энергия Кулоновское отталкивание протонов уменьшает энергию ядра. Для ядра с равномерным распределением протонов по объёму энергия кулоновского отталкивания пропорциональна или Кулоновская энергия записывается в виде
Энергия связи ядра Энергия симметрии Энергия симметрии является следствием действия принципа Паули для тождественных фермионов. В состав ядра входят фермионы двух типов – протоны и нейтроны. Если, например, попытаться создать устойчивое ядро только из А нейтронов, то нужно будет разместить их по самым нижним энергетическим состояниям. Поскольку лишь ограниченное число фермионов каждого сорта могут занять определенный энергетический уровень, то часть нейтронов придется поместить на уровни, лежащие при более высоких энергиях. Это уменьшает энергию связи ядра по сравнению с тем случаем, когда ядро из А нуклонов содержит одинаковые количества протонов и нейтронов, на величину энергии симметрии
Энергия связи ядра Энергия спаривания В зависимости энергии связи от А наблюдаются «пульсации» на уровне 1 -3 Мэ. В, которые объясняются специфическим свойством взаимодействия в системе связанных нуклонов. В атомных ядрах возникает дополнительная связь между двумя нуклонами одного типа (двумя протонами или двумя нейтронами), занимающими один и тот же энергетический уровень. Этот эффект, называемый спариванием, невелик − чтобы разорвать эту дополнительную связь нужна энергия ≈ 1 -3 Мэ. В Наличие сил спаривания разбивает все ядра на три группы: − чётно-чётные ядра. Все нуклоны в основном состоянии спарены и положительная добавка к энергии связи за счёт этого наибольшая; − нечётно-нечётные ядра. В основном состоянии не спарены по одному нуклону каждого типа и добавка к энергии связи наименьшая; − нечётные ядра. В основном состоянии не спарен один нуклон. Ярким проявлением сил спаривания является то, что среди 300 стабильных ядер почти 2/3 являются чётно- чётными, а нечётно-нечётных всего четыре Энергию спаривания записывают так, чтобы для нечётных ядер она была равна нулю.
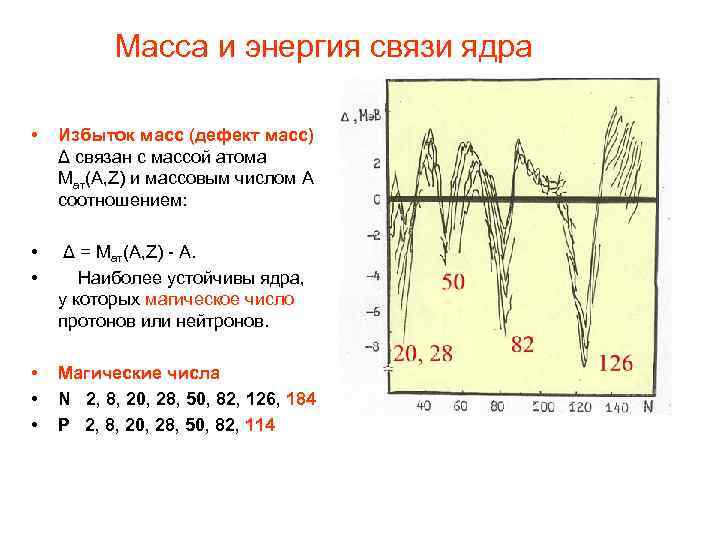Масса и энергия связи ядра • Избыток масс (дефект масс) Δ связан с массой атома Mат(A, Z) и массовым числом A соотношением: • • Δ = Мат(A, Z) - А. Наиболее устойчивы ядра, у которых магическое число протонов или нейтронов. • • • Магические числа N 2, 8, 20, 28, 50, 82, 126, 184 P 2, 8, 20, 28, 50, 82, 114
Масса и энергия связи ядра • Несложно оценить значение зарядового числа Z, при котором ядра становятся нестабильными по отношению к спонтанному распаду. Спонтанный распад ядра возникает в случае, если кулоновское расталкивание протонов ядра начинает преобладать над стягивающими ядро ядерными силами. Оценка ядерных параметров, при которых наступает такая ситуация, может быть проведена из рассмотрения изменений в поверхностной и кулоновской энергиях при деформации ядра. Если деформация приводит к более выгодному энергетически состоянию, ядро будет спонтанно деформироваться вплоть до деления на два фрагмента. При деформации ядро – не меняя своего объема – превращается в эллипсоид • При деформации не меняется первый член формулы Вайцзеккера, второй (поверхностная энергия) по абсолютной величине возрастает, а третий (кулоновская энергии) – уменьшается:
Спиновый момент частицы Спин — собственный момент количества движения частицы. Спин был первоначально введен для того, чтобы объяснить тот экспериментально наблюдаемый факт, что многие спектральные линии в атомных спектрах состоят из двух близко расположенных линий. Спин имеет квантовую природу и не связан с какими-либо перемещениями частицы в пространстве. Спин измеряется в единицах постоянной Планка и равен s — характерное для каждой частицы полуцелое или целое (включая нуль) положительное число Спин частиц может иметь только дискретный набор значений. Это одна из характерных особенностей квантовой физики.
Спиновое квантовое число s может быть как целым (включая нуль), так и полуцелым, т. е. 0, 1/2, 1, 3/2, 5/2, … , но при этом для каждой элементарной частицы он может принимать единственное присущее этому типу частиц значение. Так, спины π-мезона и К-мезона равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика. Проекция sz вектора спина S на любое фиксированное направление в пространстве (например, на ось z) может принимать 2 s + 1 значение: Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция спина может принимать лишь два значения sz = ± 1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция − 1/2, то говорят, что спин направлен вниз.
Спин ядра Ядро, как пространственно ограниченная и связанная система взаимодействующих между собой нуклонов, во многих случаях может рассматриваться в целом как одна микрочастица. Так как нуклоны, из которых состоит ядро, обладают собственным механическим моментом, или спином, а также совершают движение относительно друга (орбитальное движение относительно центра инерции ядра), то и ядра должны иметь собственный механический момент (далее просто момент) или спин. Спин ядра есть векторная сумма полных моментов отдельных нуклонов, каждый из которых складывается из орбитального момента и спина нуклона , так что 1. 6. 1. Возможна другая схема сложения моментов отдельных нуклонов, когда сначала по отдельности суммируются векторы спинов и векторы орбитальных моментов всех нуклонов, затем полученные два вектора складываются. Однако, поскольку ядерные силы не центральны и в ядре существует спин-орбитальное взаимодействие , то по этой причине в теории ядра используют первую схему.
Спин ядра Естественной единицей измерения момента импульса в квантовой механике служит постоянная Планка ħ = 1, 0546· 10 -34 Дж·с, имеющая размерность момента импульса. Вектор момента любых микрочастиц, как, впрочем, и спина ядра, обладает своеобразными свойствами. 1. Абсолютная величина вектора момента любой изолированной физической величины может принимать только дискретные значения: 1. 6. 2. где I – либо целое, либо полуцелое положительное число: I = 0, 1/2, 1, 3/2, . . . 1. 6. 3. Число I называют обычно величиной момента или квантовым числом момента. Следует особо отметить различие между модулем вектора и квантовым числом I, так как последнее является одним из чисел (1. 6. 3), используемых в формуле (1. 6. 2) для нахождения модуля вектора . Когда говорят: «момент 1/2» , то имеют в виду именно это квантовое число в формуле (1. 6. 2).
Спин ядра В формуле (1. 6. 1) квантовое число lk для орбитального момента всегда целое число, lk = 0, 1, 2, … , а нуклоны (и электрон тоже) имеют квантовое число спина s = 1/2 (спин равен 1/2). 2. Мгновенное значение вектора любого механического момента не имеет смысла по той же причине, по которой в квантовой механике не имеет смысла мгновенное значение вектора импульса. Строго фиксированное значение может иметь только абсолютная величина вектора момента (1. 6. 2) и одна из его пространственных проекций, обычно называемой проекцией на ось Z, которая обозначается как Iz. Проекция момента Iz может принимать случайным образом одно из (2 I + 1) значений, уменьшающихся на единицу: Iz = Iћ, (I– 1)ћ, . . . , -Iћ. 1. 6. 4. Реализация любой возможной проекции из набора (1. 6. 4) оказывается равновероятной. Число возможных проекций на ось Z четно, если I – полуцелое число, и нечетно, если I – целое число. Знак плюс или минус в (1. 6. 4) означает ориентацию вектора момента на выбранное направление оси Z в пространстве.
= Спин ядра Однако величины проекций Ix и Iy не имеют определенных значений и флуктуируют относительно нулевого среднего значения. Учитывая, что 1. 6. 5. имеем 1. 6. 6. Таким образом, квадраты проекций вектора момента на оси Х и Y не равны нулю. По этой причине проекция момента Iz всегда меньше абсолютной величины вектора механического момента. Действительно, согласно (1. 6. 4), максимальное значение = тогда как согласно (1. 6. 2)
Спин ядра Все перечисленные выше свойства вектора механического момента обычно демонстрируют с помощью квазиклассической модели (рис. 1. 6. 1), которая находится в определенном согласии со свойствами квантовомеханического вектора момента. Вектор момента, модуль которого вычисляется с помощью (1. 6. 2), прецессирует относительно оси Z с некоторой угловой скоростью и может ориентироваться вдоль или против направления оси Z только таким образом, чтобы его проекция на ось Z была равна одному из значений от +Iћ до –Iћ через единицу. Этот вектор никогда не может ориентироваться точно по направлению оси Z, поскольку его модуль, как отмечено выше, не равен Iћ. Поэтому, помимо его модуля, сохраняющейся во времени величиной является только одна проекция вектора – проекция на ось Z. Полное число проекций Iz вектора момента на рис. 1. 6. 1 равно (2 I + 1).
Спин ядра 3. Модуль вектора момента сложной системы, составленной из двух взаимодействующих систем с моментами и , вычисляется из выражения 1. 6. 7. обычным образом через свои квантовые числа . Сложение векторов и есть сложение их проекций как алгебраических чисел. Для поучения возможных проекций вектора каждая из проекций вектора складывается с одной из соответствующих проекций вектора . Таких проекций оказывается всего (2 I 1 + 1)(2 I 2 + 1), которые будут образовывать (2 Im + 1) векторов , , min{I 1, I 2}, Im = со следующими значениями квантовых чисел: 1. 6. 8. Соотношение (1. 6. 8) называется правилом сложения моментов в квантовой механике.
Спин ядра Поскольку каждое значение проекции из (2 I 1 + 1)(2 I 2 + 1) возможных реализуется с равной вероятностью, то относительная вероятность образования состояния со спином I´ из возможного набора значений (1. 6. 8) составит 1. 6. 9. т. е. равна отношению числа возможных проекций вектора к полному числу проекций возможных значений вектора . Величина g называется статистическим фактором или статистическим весом. 4. Любая векторная величина , характеризующая физические свойства микрочастицы, пропорциональна вектору момента : 1. 6. 10. Где a – константа, полностью характеризующая вектор.
Спин ядра В отношении спинов различных ядер наблюдаются следующие опытные закономерности: а) Для ядер с четными А спины всегда целые, а при нечетном А – всегда полуцелые. б) Четно-четные ядра (А - четное) в основном состоянии имеют спин равный нулю. Этот факт дает основания считать, что одноименные нуклоны объединяются в пары (эффект спаривания) с противоположно направленными спинами, так что суммарный момент импульса оказывается равным нулю. в) Нечетно-нечетные ядра (А - четное) имеют целочисленный спин. Это указывает на то, что разноименные нуклоны объединяются в пары с одинаковым направлением спинов, создавая единичный момент. г) Ядра с нечетным А имеют полуцелый спин в пределах от 1/2 до 9/2, что свидетельствует о том, что спины и орбитальные моменты большинства нуклонов компенсируются и не участвуют в создании спина ядра
Спин ядра, магнитный момент Магнитный момент – основная физическая величина, характеризующая магнитные свойства вещества. Магнитными моментами обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитные моменты отдельных элементарных частиц (электронов, протонов, нейтронов) обусловлено существованием у них спина (см. пояснения к (1. 6. 10)). Магнитные моменты ядер складываются из спиновых магнитных моментов протонов и нейтронов, образующих эти ядра, а также из магнитных моментов, связанных с их орбитальным движением внутри ядра по тем же правилам, по которым вычисляется спин ядра. В соответствии с (1. 6. 10) магнитный момент ядра равен 1. 6. 11. Где r – гиромагнитный множитель (отношение), равный отношению величины магнитного момента к величине механического: 1. 6. 12.
Спин ядра В (1. 6. 12) приняты следующие обозначения: е – элементарный электрический заряд; mp – масса протона; с – скорость света в вакууме; μ – безразмерное число. Проекция магнитного момента на ось Z, которая совпадает с направлением внешнего магнитного поля, будет равна, согласно(1. 6. 4): 1. 6. 13. где величина 5, 05× 10 -27 Дж/Тл 1. 6. 14. называется ядерным магнетоном Бора. Магнетон Бора является такой же универсальной единицей измерения магнитных моментов ядер, какой служит элементарный электрический заряд e для измерения заряда тел, или постоянная Планка для измерения механических моментов.
Спин ядра Точно так же безразмерное число μ служит для измерения магнитных моментов ядер в единицах ядерных магнетонов Бора , подобно атомному номеру при измерении заряда ядер в единицах е, или квантовым числам при измерении механических моментов в единицах постоянной Планка . Ядерный магнетон Бора в = 1836 раз меньше электронного М 0 магнетона Бора, который используется в атомной физике. Методы экспериментального определения спина и магнитного момента ядер тесно между собой связаны и основаны на исследовании взаимодействия магнитного момента ядра с магнитным полем. Исторически одним из первых методов определения спина ядер было исследование сверхтонкой структуры спектральных линий атомов, возникающей в результате взаимодействия магнитного момента ядра с магнитным полем , которое создается электронной оболочкой атома в месте расположения ядра. Энергия взаимодействия магнитного момента ядра с магнитным полем электронной оболочкой равна 1. 6. 15.
Спин ядра Вектор магнитного поля направлен противоположно вектору полного механического момента электронной оболочки атома и равен согласно (1. 6. 10): 1. 6. 16. Спин ядра можно также определить по расщеплению спектральных линий (эффект Зеемана) в магнитном поле, создаваемым внешним макроскопическим током, например, катушкой с током. Особенно точным методом определения магнитных моментов ядер является метод ядерного магнитного резонанса (ЯМР). Идея метода заключается в принудительном изменении ориентации магнитного момента ядра (а, следовательно, и спина), находящегося в сильном магнитном поле, под действием слабого высокочастотного магнитного поля определенной (резонансной) частоты ω0. Если образец поместить в сильное постоянное внешнее магнитное поле , то магнитный момент будет прецессировать вокруг направления (рис. 1. 6. 3) с частотой ω0.
Спин ядра, магнитный момент Энергия взаимодействия магнитного момента ядра и сильного магнитного поля равна 1. 6. 17. и соответствует низшему энергетическому состоянию атома.
Спин ядра, электрический момент Электрический заряд ядра Z не дает представления о распределении протонов в ядре. Некоторые представления о распределении электрического заряда в ядре и его структуре можно получить с помощью дипольного и квадрупольного моментов ядра. Диполем называется система из двух равных по величине зарядов q разного знака, жестко закрепленных на расстоянии d. Такая система, имея равный нулю электрический заряд, обладает свойством ориентироваться по направлению электрического поля. Так как отрицательных зарядов в ядре нет, то смещение положительного заряда (протонов) относительно нулевого (нейтронов) вызывает появление дипольного момента и ядро поворачивается в электрическом поле относительно центра инерции. Обычно рассматривают проекцию дипольного момента ядра на ось Z, совпадающую с направлением внешнего электрического поля. По определению 1. 6. 18.
Спин ядра, электрический момент где - распределение электрического заряда относительно центра инерции ядра (см. рис. 1. 6. 4), ‑ бесконечно малый заряд в точке , z – проекция радиус-вектора выбранного объема на ось Z, а интегрирование ведется по всему объему ядра. Экспериментальные измерения показывают, что ядра в основном состоянии имеют всегда равный нулю электрический дипольный момент, так как нет никаких причин, которые могли бы вызывать в ядре смещение центра масс протонов относительно центра масс нейтронов. Сильное электрическое поле может вызывать поляризацию протонов в ядре и возникновение дипольного момента. Например, электромагнитное поле γ-кванта может вызывать периодическое смещение протонов относительно нейтронов и возникновение дипольных колебаний протонов в ядре.
Спин ядра, электрический момент Другой характеристикой распределения электрического заряда в ядре является квадрупольный электрический момент Q, который не равен нулю для многих ядер, находящихся даже в стационарных состояниях. Квадрупольный момент определяет степень взаимодействие ядра с неоднородным электрическим полем. Электрическим квадрупольным моментом Q ядра называется величина, определяемая соотношением е 1. 6. 19. Для экспериментального определения квадрупольных моментов используются те же методы, что и для измерения магнитных моментов - изучение сверхтонкой структуры оптических линий в спектрах и радиочастотные методы. Взаимодействие квадрупольного момента с градиентом внутриатомного электрического поля, позволяет выяснить нарушение правила интервалов и отделить расщепление спектральных линий, связанное с наличием квадрупольного электрического момента у ядра, с расщеплением, вызванным магнитным моментом ядра, и определить квадрупольный момент ядра.
Электрический квадрупольный момент и форма ядра Внутренний электрический квадрупольный момент ядра Q 0 измеряется в системе координат ядра. Величина внешнего электрического квадрупольного момента ядер Q измеряется в лабораторной системе координат. Для аксиально-симметричного относительно оси z ядра электрическим квадрупольным моментом ядра называется величина, определяемая соотношением , где ρ (r) - плотность заряда в точке r внутри ядра. Q 0 характеризует отличие распределения заряда ядра от сферически симметричного. Для сферически симметричного ядра Q 0 = 0. При Q 0 < 0, ядро является сплюснутым вдоль оси z эллипсоидом, при Q 0 > 0 ядро - вытянутый вдоль оси z эллипсоид.
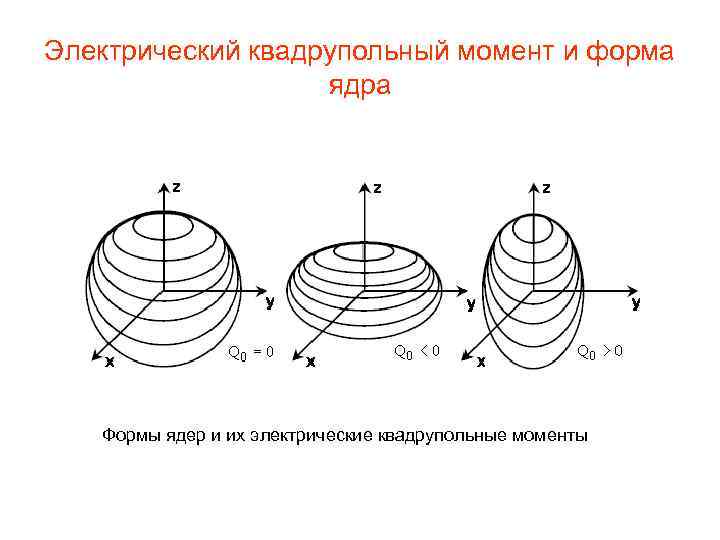Электрический квадрупольный момент и форма ядра Формы ядер и их электрические квадрупольные моменты
Электрический квадрупольный момент и форма ядра • Внешний электрический квадрупольный момент Q связан с внутренним электрическим квадрупольным моментом Q 0 соотношением • где J - спин ядра. Оси x', y', z' совпадают с главными осями ядра, x, y, z совпадают с главными осями градиента поля
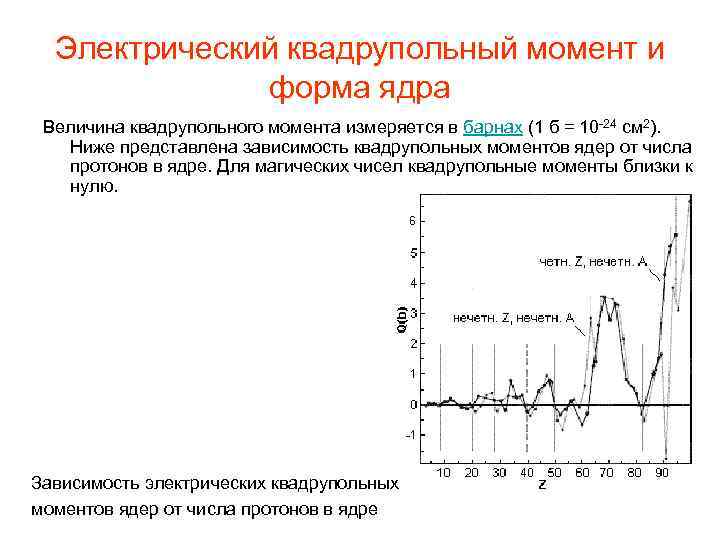Электрический квадрупольный момент и форма ядра Величина квадрупольного момента измеряется в барнах (1 б = 10 -24 см 2). Ниже представлена зависимость квадрупольных моментов ядер от числа протонов в ядре. Для магических чисел квадрупольные моменты близки к нулю. Зависимость электрических квадрупольных моментов ядер от числа протонов в ядре
Спин ядра • • Изоспин ядер и нуклонов Как основное, так и возбужденные состояния ядер характеризуются квантовыми числами, которые называются изоспином и проекцией изоспина. (В литературе эти квантовые числа обозначаются обычно либо символами T и Tz, либо I и Iz ). • Введение этих квантовых чисел связано с тем фактом, что ядерные силы инвариантны относительно замены протонов на нейтроны. Это особенно ярко проявляется в спектрах т. н. ”зеркальных” ядер, т. е. ядер–изобар, у которых число протонов одного равно числу нейтронов другого. Для всех известных пар таких ядер имеет место подобие спектров низших возбужденных состояний: спины и четности низших состояний одинаковы, а энергии возбуждения близки. С точки зрения теории изоспина, нейтрон и протон являются одной и той же частицей – нуклоном с изоспином I = 1/2 – в двух разных состояниях, различающихся проекцией изоспина на выделенную ось (Iz= I 3) в пространстве изоспина. Таких проекций для момента I = 1/2 может быть только две: Iz = +1/2 (протон) и Iz = – 1/2 (нейтрон). Квантовая теория изоспина построена по аналогии с теорией спина. •
Спин ядра • Однако пространство изоспина не совпадает с обычным координатным пространством. • Система Z протонов и N нейтронов – ядро - имеет проекцию изоспина • Iz(A, Z) = Z. (+1/2) + N. (-1/2) = (Z - N)/2. • Изоспин системы нуклонов является векторной суммой изоспинов составляющих: Ядерные (т. е. сильные) взаимодействия не зависят от проекции изоспина, или, точнее, сильные взаимодействия инвариантны относительно вращений в изоспиновом пространстве. Однако от величины изоспина ядерные силы зависят!
Спин ядра • Низшим по энергии состояниям системы нуклонов, т. е. основным состоянием ядра, является состояние с возможным низшим значением изоспина, которое равно • I 0 = |Iz| = |(Z - N)/2| • Возбужденные состояния ядер могут иметь более высокие значения изоспина, но с той же проекцией. Таким образом, характеристиками уровней данного ядра являются энергия, спин состояния, четность состояния и изоспин. Обычно два последних квантовых числа указываются как JP, I.